基于粒子滤波的视觉跟踪器的设计与实现*
2013-08-13温诗伟
杨 戈,温诗伟,黄 静
(1.北京师范大学 珠海分校 信息技术学院,广东 珠海 519087;2.北京大学 深圳研究生院 深圳物联网智能感知技术工程实验室,广东 深圳518055)
视觉跟踪是通过对图像序列中的运动目标进行检测、识别、跟踪,获得运动目标的运动参数,通过进一步处理与分析,实现对运动目标的行为认识,以完成对运动目标的跟踪[1-2]等更高级的任务。处理理背景复杂多变的目标运动的跟踪问题,要运用到现阶段各相关领域相结合的识别跟踪算法,如均值漂移算法(Mean Shift)[3],卡尔曼滤波算法(Kalman)、粒子群跟踪算法(Pso)[4],以及粒子滤波跟踪算法PF(Particle Filter)[5]。粒子滤波算法适合处理非线性系统的目标跟踪问题,它摆脱了解决非线性滤波问题时,随机量必须满足高斯分布的制约[6]。因此,粒子滤波能够比较精确地表达基于观测量和控制量的后验概率分布,可用于解决即时定位与地图构建SLAM(Simultaneous Localization and Mapping)问题。
1 粒子滤波算法
粒子滤波的思想[7],即基于蒙特卡洛方法(Monte Carlo Methods),它是利用粒子集来表示概率,可以用在任何形式的状态空间模型上。基于粒子滤波的视觉跟踪的核心思想是利用一组加权的随机样本 (也称为粒子){Xk(i),近似表示视觉目标后验概率p(Xk|Z1:k)。简单来说,粒子滤波法是指通过寻找一组在状态空间传播的随机样本对概率密度函数p(xk|zk)进行近似,以样本均值代替积分运算,从而获得状态最小方差分布的过程。其中k为离散时间;Xk为状态向量,表示其在二维图像域上的位置;Zk为系统观测值,表示颜色分布向量。这里的样本即指粒子,当样本数量N→∝时可以逼近任何形式的概率密度分布。采用数学语言描述如下:对于平稳的随机过程,假定k-1时刻系统的后验概率密度为p(xk-1|zk-1),依据一定原则选择n个随机样本点,k时刻获取测量信息后,经过状态和时间更新过程,n个粒子的后验概率密度可近似为p(xk|zk)。随着粒子数目的增加,粒子的概率密度函数逐渐逼近状态的概率密度函数q(x0:k|z1:k)[8]。
算法的一般描述:
(1)初始化:取 k=0,按后验概率密度函数 p(xk|zk)抽取 N 个样本点,i=1,…,N。
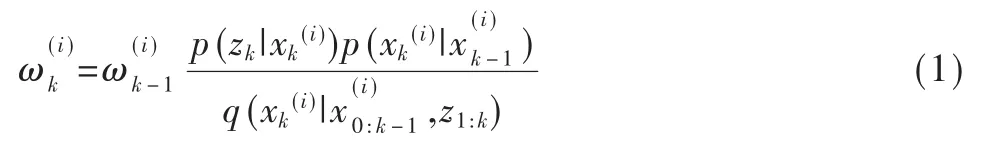
其中,辅助变量i表示k-1时刻采样粒子的索引。若采用一步转移后验状态分布,该式可简化为
(4)归一化权值:

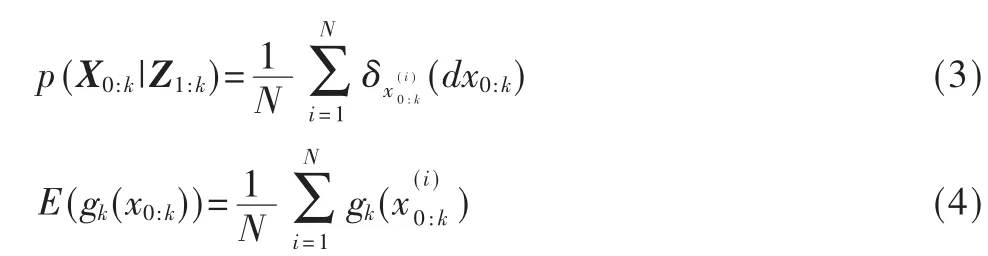
其中,d为 Bhattacharyya距离。
(7)k=k+1,重复步骤(2)~步骤(6)。
2 颜色分布模型
本文对视觉跟踪器的跟踪目标特征模型是加权颜色直方图。将目标区域化成m个子区域,统计图像序列中每个像素点落在相应子区域中的频数,得到颜色直方图。目标模型与观测模型相似度的计算是通过引入Bhattacharyya公式[9],和Bhattacharyya系数ρ观测模型的参考颜色密度q,同样将粒子的加权颜色直方图表示为q={q(u)}u=1…m,它与目标预测状态的颜色密度p={p(u)}u=1…m的匹配度用Bhattacharyya系数ρ或Bhattacharyya距离d表示,其中 ρ∈[0,1]。


其中ρ的值越大或d的值越小,表明目标模型与观测模型的颜色密度的相似度越高。最后,用权值最大粒子的位置作为目标的位置。
3 标准粒子滤波的视觉跟踪算法
(1)初始化:令k=0,人工手动选取目标参考模型 Xc,并计算其颜色分布{q(u)}u=1,…,B;同时,根据先验分布 p(X0)建立初始状态样本集
(4)视觉目标状态估计输出:根据式(3)、式(4)计算 k时刻视觉目标状态的MMSE(Minimum Mean Square Error)最小均方误差估计
②产生[0,1]上均匀分布的随机数u;
(6)令 k=k+1,返回步骤(2)。
根据粒子滤波算法的描述,本文对视觉跟踪器的框架设计如图1所示。
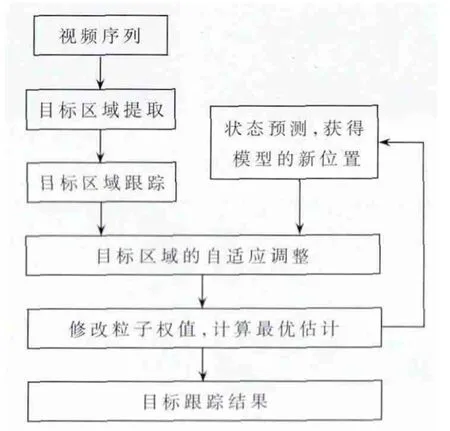
图1 视觉跟踪器的跟踪目标流程图
4 实验与结果分析
4.1 实验环境
实验的硬件环境:CPU型号:Intel酷睿 i5 3210 M,CPU主频为 2.5 GHz,内存为4 GB,显存为2 GB。
实验的软件环境:操作系统为Windows 7,编程环境为Microsoft Visual C++6.0,所用函数库为OpenCV,MFC。
4.2 实验结果与分析
采用基于加权颜色直方图粒子滤波的视觉跟踪器对目标进行跟踪的。
本文将基于加权颜色直方图的粒子滤波算法用于目标人物的实时跟踪。实验是在VC++6.0和OpenCV的环境下进行,矩形为人为设定,每帧图像的大小为640×480像素,粒子数N=150。图2所示为对小件物体的运动目标的视觉跟踪,并把粒子样本显示出来,如图方框中的粒子,粒子分布符合高斯分布。图3所示为对女生的运动目标的视觉跟踪,图中矩形内部是待跟踪的目标人物,矩形为人为设定,用基于加权颜色直方图的粒子滤波方法对具有特定颜色的目标进行跟踪,计算每帧图像每个像素点的颜色概率分布直方图,对每个像素进行加权处理,只需保留样本中权值大的粒子,抛弃权值小的粒子,这样就大大减少了计算。实验结果表明,粒子滤波跟踪算法对系统资源要求不高,计算时间少,一帧平均处理时间为170 ms。而在有遮挡的运动目标的图像序列当中,每帧图像的大小为640×480像素,粒子数 N=150,对有遮挡的运动目标能够有很好的鲁棒性,平均每帧跟踪时间为350 ms。图4所示为对男生的运动目标的视觉跟踪,对有遮挡的目标,跟踪的准确率有所下降;而有遮挡的运动目标则有很好的鲁棒性,平均每帧跟踪时间为350 ms。表1为图像序列在这两种情况下,跟踪算法的成功率的比较,当跟踪窗口没有跟踪目标视为失败。

图2 对小物体(书)的视觉跟踪(粒子样本显示)

图3 对女生的运动目标的视觉跟踪

图4 对男生的运动目标的视觉跟踪(有遮挡)
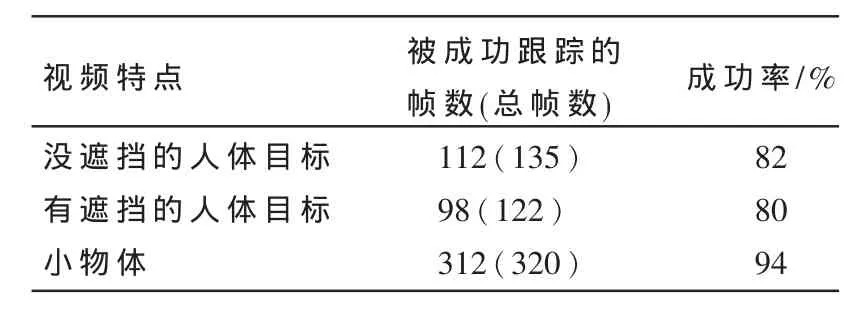
表1 跟踪算法跟踪成功率的比较
本文阐述了通过基于特征跟踪策略,应用OpenCV函数库进行对图像序列的运动目标进行跟踪和监测,实现了基于加权颜色直方图粒子滤波的视觉跟踪器。通过实验表明,基于加权颜色直方图的粒子滤波方法计算效率高,鲁棒性好,实现了对彩色物体的实时跟踪。
[1]侯志强,韩崇昭.视觉跟踪技术综述[J].自动化学报,2006,32(4):604-612.
[2]杨戈,刘宏.视觉跟踪算法综述[J].智能系统学报,2010,5(2):96-102.
[3]周芳芳,樊晓平,叶榛.均值漂移算法的研究与应用[J].控制与决策,2007(8):841-847.
[4]窦永梅.基于粒子群算法和卡尔曼滤波的运动目标跟踪算法[D].太原:太原理工大学,2011.
[5]王法胜,郭权.视觉跟踪中的粒子滤波算法研究进展[J].山西大学学报(自然科学版),2011,34(4):528-533.
[6]胡昭华,樊鑫,梁德群,等.基于双线非线性学习的轨迹跟踪和识别[J].计算机学报,2007,30(8):1390-1397.
[7]吴长江,赵不贿,郑博,等.基于 FPGA的动态目标跟踪系统设计[J].电子技术应用,2010,36(3):45-50.
[8]李由,张恒,李立春.基于多测量融合的粒子滤波跟踪算法[J].国防科技大学学报,2007,29(5):27-30.
[9]杨柳,张宝亮,赵建,等.基于改进粒子滤波算法的人体运动跟踪[J].电子技术应用,2007,33(11):74-79.
