基于GPU的二部图联合聚类并行算法研究

张宇，刘坡，杨敏华，龚建华，3，黄明详

（1.中南大学地球科学与信息物理学院，湖南 长沙 410083；2.中国科学院遥感与数字地球研究所遥感科学国家重点实验室，北京 100101；3.浙江中科空间信息技术应用研发中心，浙江 嘉兴 314100；4.环境保护部信息中心，北京 100101）

0 引言

空间聚类作为聚类分析的一个研究方向，是指将空间数据集中的对象分成由相似对象组成的类，同类中的对象间具有较高的相似度，而不同类中的对象间差异较大［1］。空间聚类分析是空间数据挖掘与知识发现的主要手段之一，已广泛应用于地理学、地质学、气象学、地图学、天文学及公共卫生等诸多领域。但是由于空间数据的多尺度、高维度、模糊性等特点，造成空间聚类算法的创新研究困难较大。

二部图聚类算法作为空间聚类算法的一种，以图的形式表明数据集中数据间的关系，用以寻找不同要素间的对应关系。要素集合根据不同的原则分割成2个不同的候选集合，候选集中每个要素具有相近的空间关系或者非空间关系，二部图聚类算法旨在探究两个或多个要素集中要素间的相关性，广泛应用于文本查询和检索等领域［2，3］。二部图也应用于解决空间聚类问题，利用距离、边距以及相应的B矩阵来获得空间聚类知识，利用图嵌入方法进行影像分类［4］。利用二部图联合聚类分割可以解决异质数据的联合聚类分割问题［5，6］。海量空间数据的本身需要大量运算，现有的基于CPU的串行计算很难达到实时计算的要求，传统的采用建立空间索引的方法来加速搜索效率［7－9］，如文献［10］中提出了基于空间联合索引计算邻接矩阵的方法来计算空间聚类簇，该方法基于页访问序列，利用了限制的缓冲空间，通过启发式的对称聚类等方法获得类别空间信息。GPU的出现，带来了高性能计算的时代，统一计算设备架构（CUDA）的推出，为高性能计算开创了新时代［11，12］。文献［13］将 GPU 引入 K均值聚类算法中，利用GPU高度并行的特点可以明显提高聚类的速度。

多源空间数据的匹配，是空间数据合并、更新的基础，具有巨大的研究价值，而且多源空间数据匹配问题本身就是空间数据聚类的问题［14］。本文将GPU引入二部图匹配的联合聚类算法的过程中，以多源空间数据的匹配为例，首先将空间数据的匹配分解成一个二部图匹配的问题，进而验证GPU并行计算对空间聚类算法效率的影响和不同储存器对计算效率的影响。

1 二部图联合聚类

二部图G（V，E）表示要素间的空间关系，其中V用于表示空间要素索引的节点，E用于表示有关系空间要素索引的连线。如果空间中的两个要素集中要素存在关系，则有E≠0，E将这两个空间要素连接起来。如图1a、图1b所示，用A、B两个地理要素集合表示同一个地区不同时相的数据，数据集A中包含有要素（A1，A2，A3），数据集B 中包含有要素（B1，B2，B3），可以用图1c表示要素之间的叠置关系。该问题是一个典型的二部图联合聚类问题，可用二部图聚类算法判定空间要素间的对应关系。

图1 基于叠置关系的空间聚类Fig.1 Co－clustering based on overlay relationship

二部图聚类算法主要的流程如图2所示：1）计算要素间的空间关系，本文以叠置关系为判断依据。2）根据要素的空间关系，构建二部图关系，即构建关系矩阵及邻接矩阵。3）根据邻接矩阵，进行二部图联合聚类，每次聚类后计算判断矩阵中非0要素的数目的变化，直到要素的数目不变为止。4）根据最终的联合聚类结果，提取不同要素间的对应关系。

图2 二部图聚类Fig.2 Bipartite graph co－clustering

1.1 空间关系

确定两个要素集间的拓扑关系和权重是构建二部图的基础。空间拓扑关系一般采用9交模型描述空间数据的拓扑关系［15］。为了加快计算的速度，可利用plane－sweep［7］、TR＊树［8］和R树［9］等算法建立空间索引以加快要素空间关系的搜索，本文主要计算要素之间的叠置关系。

1.2 构建二部图

确定两个地理要素集中每个要素的对应关系之后，需要进一步将有关系的要素都集中到同一个空间要素簇下。Huh等提出利用邻接关系矩阵计算空间要素的聚类集［14］。空间数据之间多对多关系由于涉及两个要素集中的多个要素，较难确定聚类集。这可以通过如下的过程来判断：假设一个要素集中的要素与另一个要素集中的多个要素重叠，则将多个要素合并为一个连续要素，如果这个合并要素又与前一个要素集中的多个要素重叠，多个重叠要素同样进行合并，反复进行这个过程直到得到合并要素的关系为1∶1为止［14］。假定两个地理要素集分别为Ai（i＝0，1，2，3，…，m），Bj（j＝0，1，2，…，n），对于每个地理要素集中的要素，都有Ai∈A，Bj∈B。如果两个要素存在叠置关系，则Ai与Bj在二部图上存在边，Ai与Bj的地理编码可视为连接边两端的节点。假设二部图中两地理要素集中要素间的边权重都为1，构建关系矩阵C。其中，C中每一行表示要素集A中每个要素的地理编码，C中每一列表示要素集B中每个要素的地理编码，用于表示Ai与Bj的叠置关系，可表示为：

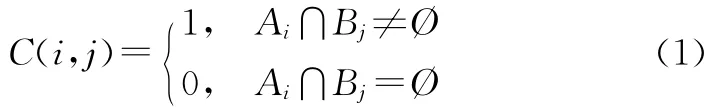
在图1中，假设数据集A和B中要素间对应关系为（A1，B2，B3），（A2，A3，B3），由于要素集A 中要素记录为矩阵C中的行，要素集B中要素记录为矩阵C中的列，矩阵C表示为：

构建邻接矩阵C′，其中I为单位矩阵，C′表示节点间所有的邻接关系（包括自相邻关系）：

1.3 矩阵运算和确定关系

对邻接矩阵C′连续自乘，直到所有为0的元素值不再发生变化，便可得到结果矩阵，其中每一行非0实体表现出要素间的邻接关系。图1中的邻接矩阵C′自乘3次后，矩阵元素为0的位置不再发生变化。为了简化计算结果，将矩阵中所有的非0元素表示为1，结果矩阵C″表示C′自乘3次之后的结果，如式（4）所示：

其中：C″的第一行表示得到空间聚类簇（A1，A2，A3）与（B2，B3）间3∶2的对应关系。第四行中，只有一个要素，其余位置处均为0，对应的要素为B1，表示要素集A中没有任何要素与B1对应。

2 GPU并行算法设计

CUDA的基本思想是将应用程序映射到GPU以获得较大的性能提升，尽量的开发线程级并行算法，将GPU作为超大规模数据并行协处理器，让GPU运行一些能够被高度线程化的程序，充分发挥GPU并行处理能力并极大提高单个计算节点的计算性能。CUDA采用单指令多线程（SIMT）执行模型，执行数据宽度将作为硬件细节被隐藏起来，硬件可以自动地适应不同执行宽度，而且每个线程的寄存器是私有的，线程间只能通过共享存储器和同步机制通信。GPU采用的是由硬件管理的轻量级线程，实现零开销线程切换，用计算隐藏延迟。

2.1 并行算法设计分析

由于空间数据计算数量的扩大，导致构建邻接矩阵的维度增大，计算速度降低。采用GPU并行加速算法，计算时间和电脑资源的开销将会减少。可以利用GPU高度并行的特点快速提高二部图聚类算法过程中的邻接矩阵运算效率，主要包括矩阵自乘和计算矩阵中非0的个数。

2.1.1 矩阵自乘并行性分析 假设一个M×N大小的关系矩阵C，其邻接矩阵C′大小为（M＋N）×（M＋N）。对于矩阵自乘，由于每个要素都是独立计算的，理论上可同时运行（M＋N）×（M＋N）线程来同步计算，但是由于硬件的限制，每次启动的线程块和每个块中线程的数量都有限制。每一个内核的配置项包括问题的分块数griddim及每个块内的线程数目blockdim，增加线程块中线程数目可能会降低在多处理器中投入运行的实际线程块数，降低并行度。假设矩阵计算中每个块的大小为Width×Length，邻接矩阵可以划分为（M＋Width－1）／16×（N＋Length－1）／16个块，每个块中有Width×Length线程执行计算。

GPU以warp为单位调度和执行，每个warp拥有32个线程，若线程调度数目不足32个，则会因warp块填充不足而造成计算资源的浪费，损失部分效率。而对于存储器的访问，是以half－warp为单位进行的，因此提高运算效率就要使划分的线程矩阵维度为16的倍数。对于GeForce 9800GT，由于每个SM（流多处理器）中最多有768个线程，8个SP（流处理器），处理效率最佳时，线程块的数目应满足768／（Width×Length）＜8。

2.1.2 计算矩阵非0元素并行性分析 当邻接矩阵相乘次数大于等于2时，需要判断矩阵中非0元素的个数。对于（M＋N）×（M＋N）要素的邻接矩阵非0元素个数的计算，可视为并行归约的过程。可以将该循环计算分解为（M＋N）×（M＋N）线程以完成计算，考虑不同的分块和分线程完成计算，假设每个块中有512个线程，过程如下：第一次循环，只有i＝0，2，4，…，510线程执行计算，即每个线程与其后跨度为1的元素加操作；第二次循环，只有i＝0，4，8，12，…，508线程执行计算，即每个要素与其后跨度为2的元素加操作；依次类推……直到最后一次循环，即i＝0线程执行计算。此时线程i＝0中记录的结果即为要素中非0元素的个数。

2.2 并行算法设计优化

CUDA内部存在6种存储器，分别是寄存器、局部存储器、共享存储器、全局存储器、常数存储器和纹理存储器，应依据具体研究内容选择合适的存储设备从而最大限度地提高算法的效率，本文探讨采用全局存储器和共享存储器完成计算。

2.2.1 全局存储器 全局存储器使用的是普通的显存，存储内核中输入输出数据，容量较大，整个网格中的任意线程都能读写全局存储器的任意位置。在计算能力较低的GPU设备中，缺少对数据的缓存，采用全局存储器操作数据时将导致400～600个时钟周期的延迟，而且在计算过程中有许多重复的数据存储访问。因此，必须最小化对全局存储器的访问并应设计考虑SM中数据重用。

使用全局存储器进行邻接矩阵运算时，GPU可实现在GPU－DRAM的任何位置读取到GPU中的聚集操作。如果计算的矩阵大小不超过GPU的计算能力，可利用CUDA的API中的cudaMemcpy（）一次性将邻接矩阵数据由内存全部加载到GPU全局存储器中。

2.2.2 共享存储器 共享存储器位于每个SM内，同一个SM上的线程可访问一个共享存储器，实现高速数据交换。通过线程间的合作，可以将全局存储器的流量减少到原来的1／16，避免了数据的重复读取和存储，提高了运算效率。共享存储器位于GPU片内，速度比局部存储器、全局存储器快很多。在不发生bank冲突的情况下，共享存储器的延迟几乎只有局部存储器或全局存储器的1／100，访问速度和寄存器相当。对共享存储器的访问是以半个warp为单位，访问将会以前16个线程或后16个线程的方式进行。半warp中的线程访问的数组元素分别属于不同bank时，不会发生访问冲突；当半warp中的线程访问的数据元素处于同一个bank时，其读写操作不能同时进行，发生访问冲突，造成运算错误。考虑到每个程序中字节的大小，算法以4的倍数设置进行等间隔的访问以避免冲突。

共享存储器在每个流处理器中只有16KB的存储空间，算法要考虑到共享存储器的大小。设计每个线程块的共享空间大小为16×16，对于实验中处理的int类型的变量，每个共享存储空间中的数据小于16KB。若邻接矩阵不超过GPU的运算能力，则将邻接矩阵全部调入全局存储器中，每个SM中的共享存储器分别对应处理一个矩阵块。根据矩阵元素的标识将相应的数据调入对应的共享存储器中进行运算，用矩阵块Ai中的每一行乘以矩阵块Bj中的每一列，并将计算结果按照数据对应行列进行相加计算，接着依次对该行列中相应的矩阵块相加，将结果保存在矩阵C中的相应位置处。由于同一个线程块共用一个共享存储器，因此，每个线程块中各线程可以重复利用加载到共享存储器中的数据，减少了数据的重复存取。最后将运算结果由全局存储器载入到内存中。

3 实验及分析

实验采用GeForce 9800GT显卡，显存容量为1 G，计算能力为1.1，时钟频率为1.50GHz，有12个流多处理器，每个流多处理器中有8个流处理器，每个流处理器中有16KB的共享存储器。采用浙江海盐地区不同时相的多尺度数据，验证本文的算法和不同配置情况下的GPU运行效率。对于不同来源的空间数据，首先将其投影到统一的空间坐标体系下，然后确定不同空间数据集间的拓扑叠置关系，根据式（3）构建邻接矩阵，通过GPU并行计算确定要素之间的关系，得到空间聚类结果。实验在vs2008.net环境下，利用 ArcEngine 9.3，CUDA Toolkit 5.0工具包开发，并将并行算法封装为动态链接库（DLL），完成整个实验过程。

3.1 CPU串行和GPU并行比较

针对同一个地区的多尺度和多时相的两个地理要素集做空间联合聚类运算，先执行CPU串行计算，再分别执行基于GPU全局存储器和基于GPU共享存储器的并行计算，计算时间统计如表1所示。

由表1可以看出，基于GPU共享存储器的计算效率最高，其次是基于GPU全局存储器的计算效率，而基于CPU串行计算的效率最低。利用GPU并行计算比利用CPU串行计算的执行效率高。此实验中的邻接矩阵大小为1 103×1 103，矩阵自乘次数为12次，矩阵元素类型为整型，处理数据量大小为55.69MB，分别计算这三者的计算速率：1）GPU全局存储器并行计算：55.69MB÷13.726s≈4.1 MB／s；2）GPU 共享存储器并行计算：55.69MB÷0.9935s≈56.1MB／s；3）CPU串行计算：55.69MB÷853s≈0.065MB／s。可以看出，GPU共享存储器运算效率是GPU全局存储器运算效率的14倍，是CPU串行计算效率的858倍。在此类情况下，GPU并行计算应使用共享存储器提高算法的效率。

表2是不同空间二部图联合聚类中，执行GPU共享存储器计算与执行CPU串行计算的时间和加速比。从表中可以看出，随着矩阵维度的扩大，对应的循环次数不确定，并且加速比有增大的趋势，但是达到一定的维度后，趋于稳定。其中在矩阵维度为1 103时，加速比最大，表明此时GPU共享存储器运算效率是CPU串行计算效率的858倍。

表2 不同维度下的串并行性能比较Table 2 Comparison of serial and parallel performance under different dimensional

3.2 GPU在处理不同数据量时的效率

使用GPU共享存储器在处理不同数据量时，进行空间聚类并行计算的效率有明显的不同，实验选取同一地区的多时相、多尺度数据进行空间二部图联合聚类，统计结果如表3所示。由表3可知，由于空间要素聚类关系的多样性，构建的邻接矩阵的维度明显不同，邻接矩阵的循环次数也表现出无规律性。但随着矩阵维度的增大，并行计算中单次循环平均耗时也越来越多。运算效率不仅与维度相关，还与循环次数相关。如果两个要素集中要素间存在叠置关系，则对应邻接矩阵中的权重为1，矩阵中权重为1的矩阵元素的数目决定着矩阵的复杂度以及最终的运算效率。直到所有的关系要素都合并为1∶1，得到最终的空间聚类簇。

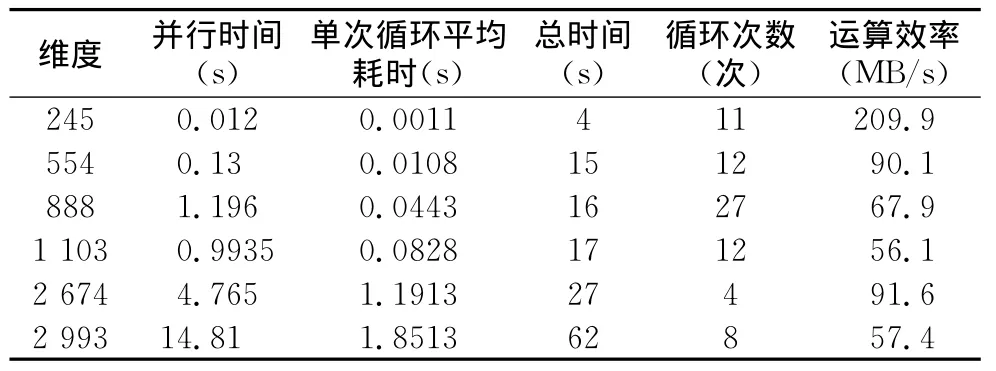
表3 不同维度下GPU共享存储器运算结果Table 3 Calculation result of GPU shared memory under the different dimensional

3.3 Warp占有率对GPU运算效率的影响

通过实验对经过优化的并行二分图聚类算法在设计中的各种参数对于系统性能的影响进行分析。图3表示的是每个线程块中不同线程数量对warp占有率的影响，其中三角形标记处是设计的线程模块的分配大小，每个线程块中有256个线程，此时warp占有率最高。图4表示的是不同寄存器数量对warp占有率的影响，其中三角形标记处是每个线程分配的寄存器个数，每个线程中拥有的寄存器数量为8，此时warp占有率最高。在每个线程的寄存器数量多于32个时，每个SM中最多有8 129个寄存器文件，此时warp占有率为0。图5表示的是不同的共享内存对warp占有率的影响，其中三角形标记处是每个块分配的共享存储器大小，每个线程块中拥有的共享内存大小为1 024bytes，此时warp占有率最高。当共享内存大小大于16KB时，由于每个SM中最多有16KB共享内存，此时warp占有率将降为0。本文中线程的划分正好满足此类条件，warp占有率最佳。

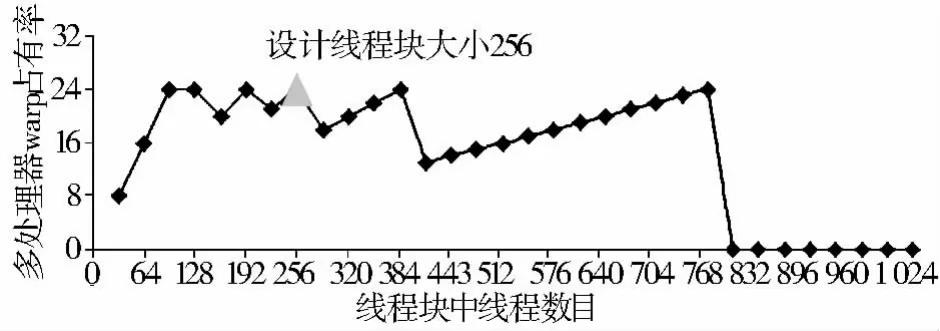
图3 线程数对warp占有率的影响Fig.3 The affection of threads to warp occupancy

图4 寄存器对warp占有率的影响Fig.4 The affection of registers to warp occupancy

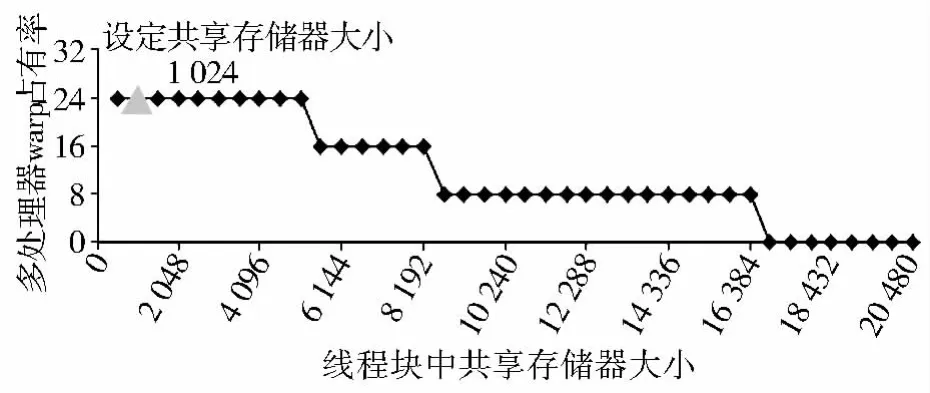
图5 共享内存对warp占有率的影响Fig.5 The affection of shared memory to warp occupancy

4 结论

空间聚类算法是一个计算密集型算法，对计算资源有着巨大的需求，对于有潜在并行的算法，GPU的并行计算可以显著提高聚类的计算效率。根据GPU硬件特征和研究对象的不同划定GPU线程的大小，使运算效率最优化。特别是海量空间数据聚类，GPU并行计算将会有明显的优势。本文将GPU并行计算运用到二部图联合聚类算法中，实验结果表明，基于GPU的并行计算将会给空间联合聚类算法的效率带来显著的提升。此外，空间索引也是提高数据处理速度的一种有效的手段，如何将空间数据索引与GPU并行计算结合，将是下一步研究的方向。

［1］ 席景科，谭海樵.空间聚类分析及评价方法［J］.计算机工程与设计，2009（7）：1712－1715.

［2］ 张军伟，王念滨，黄少滨，等.二分K均值聚类算法优化及并行化研究［J］.计算机工程，2011（17）：23－25.

［3］ ZHA H，HE X，DING C，et al.，Bipartite graph partitioning and data clustering［A］.Proceedings of the Tenth International Conference on Information and Knowledge Management［C］.2001.25－32.

［4］ CZECH W.Invariants of distance K－graphs for graph embedding［J］.Pattern Recognition Letters，2012，33（15）：1968－1979.

［5］ FERN X Z，BRODLEY C E.Solving cluster ensemble problems by bipartite graph partitioning［A］.Proceedings of the Twenty－First International Conference on Machine Learning［C］.2004.36.

［6］ REGE M，DONG M，FOTOUHI F.Bipartite isoperimetric graph partitioning for data co－clustering［J］.Data Mine Knowledge Discovery，2008，16（3）：276－312.

［7］ BRINKHOFF T，KRIEGEL H P，SCHNEIDER R，et al.Multistep processing of spatial joins［J］.ACM，1994，23（2）：197－208.

［8］ ZHANG J，YOU S，GRUENWALD L.High－Performance Spatial Join Processing on GPUs with Applications to Large－Scale Taxi Trip Data［R］.2012.

［9］ BRINKHOFF T，KRIEGEL H P，SEEGER B.Parallel processing of spatial joins using R－trees，data engineering［A］.Proceedings of the Twelfth International Conference，IEEE［C］.1996.258－265.

［10］ SHEKHAR S，LU C T，CHAWLA S，et al.Efficient join－index－based spatial－join processing：A clustering approach［J］.IEEE Transactions on Knowledge and Data Engineering，2002，14（6）：1400－1421.

［11］ OWENS J D，HOUSTON M，LUEBKE D，et al.GPU computing［A］.Proceedings of the IEEE［C］.2008，96（5）：879－899.

［12］ 肖汉，周清雷，张祖勋.基于多GPU的Harris角点检测并行算法［J］.武汉大学学报（信息科学版），2012（7）：876－881.

［13］ FARIVAR R，REBOLLEDO D，CHAN E，et al.A parallel implementation of K－Means clustering on GPUs［A］.Proceedings of International Conference on Parallel and Distributed Processing Techniques and Applications（PDPTA）［C］.Las Vegas，Nevada，USA，F，2008.340－345.

［14］ HUH Y，YU K，HEO J.Detecting conjugate－point pairs for map alignment between two polygon datasets［J］.Computers，Environment and Urban Systems，2011，35（3）：250－262.

［15］ 李成名，陈军.空间关系描述的9－交模型［J］.武汉测绘科技大学学报，1997，22（3）：207－211.