栅格地理数据模糊C均值聚类算法的并行化研究

王维一，裴韬，秦承志

（1.中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室，北京 100101；2.中国科学院大学，北京 100049）

0 引言

随着空间信息技术和模糊理论的发展，模糊C均值聚类（Fuzzy C－Means，FCM）作为地学应用中的一种常用算法，被广泛应用于多图层栅格地理数据分析中［1－4］。然而，FCM算法属于计算密集型算法，计算耗时长，现今随着地学中高分辨率数据的应用、输入图层数的增加以及研究尺度的扩展，地学计算的数据量急剧增加，面对如此海量数据，传统的串行算法在计算效率和性能方面越来越不能满足需要，因此急需将串行FCM并行化。

自从Kwok等提出并实现了基于MPI的并行FCM算法用于商业数据以来［5］，地学专家、学者对FCM的并行化算法进行了不少研究。Gong等基于MPI的FCM并行算法使人对遥感影像进行模糊聚类分析获得了令人满意的线性加速比［6］；Petcu等针对多光谱遥感影像，提出了一种基于MPI的FCM并行算法，也得到较好的线性加速比［7］。但是这些方法只适合于规则的栅格数据。Liu等提出了一种基于图形处理器（Graphics Processing Unit，GPU）的FCM 并行算法［8］。

由于地学应用研究区域的不规则性，并行算法采用按区域大小均匀划分（如按行、列划分和棋盘式划分［9］）方法导致各节点负载不均衡，并行效率低。针对这个问题，王少文等提出了按计算强度（即单位像元的计算量）划分的方法，并将该方法应用于反距离加权插值和空间热点探测［10］。然而该方法实现案例较少，且主要针对单图层。

本文针对多图层栅格地理数据的FCM算法进行并行化，采用按计算强度均匀划分数据的方式，并通过实验与采用按区域大小均匀划分数据方式实现的FCM并行算法进行了性能比较。

1 模糊C均值聚类算法

FCM是用隶属度确定每个数据点属于某个聚类程度的一种聚类算法。Bezdek于1973年提出了该算法，是早期硬C均值聚类（HCM）方法的一种改进［11］。FCM与HCM的主要区别在于FCM用模糊划分，使得每个给定数据点用值在［0，1］间的隶属度确定其属于各个组的程度，而HCM用的是｛0，1｝硬划分。

FCM算法可表示成数学规划问题：

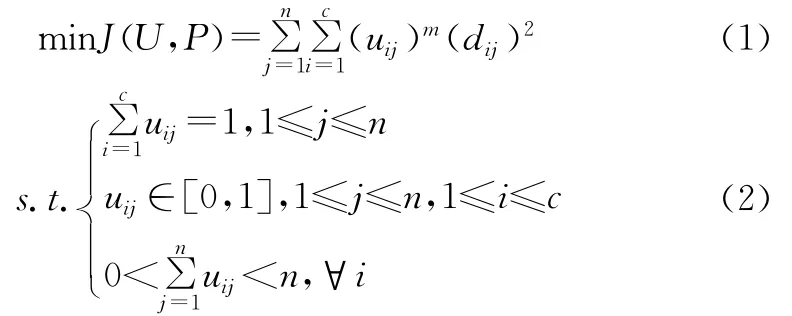
其中，U为模糊隶属矩阵，P为聚类中心，uij为模糊隶属矩阵U中表示第j个元素属于第i个中心的隶属度值，m为加权指数，dij表示第j个元素与第i个中心的距离，n表示数据集个数，c为聚类中心数。

求解上述数学规划的过程如下：

步骤一：初始化，设定聚类中心数c，2≤c≤n，n是数据集中元素的个数，最大迭代次数Lmax，设定迭代停止阈值ε＞0，初始化聚类中心P（0），设定迭代计算器k＝0。

步骤二：按式（3）更新模糊隶属度矩阵U（k）：

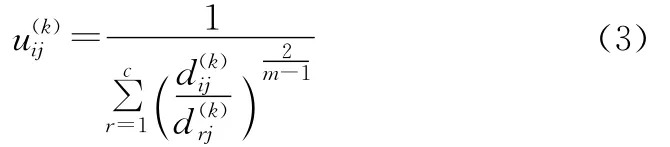
步骤三：按式（4）更新聚类中心P（k＋1）：

步骤四：用一个矩阵范数 ‖·‖ 比较 P（k）与P（k＋1），若‖P（k）－P（k＋1）‖≤ε，则停止迭代，并输出模糊隶属度矩阵U和聚类中心P，否则令k＝k＋1，转到步骤二进行下一次迭代。

两首译诗只在几个关键词的选择和使用上不同，就构建出截然不同的两种语境，两种情景模型，这是由于译者对原诗的理解不同。从心理学的角度看，由于第一首译诗的译者与诗人对“辽西”的认知环境不同，直接导致两人对同一首诗的理解迥然不同。在诗人看来，“辽西”既是地名又会激活扩散到“战争”的意义，而第一首译诗的译者没有这种背景知识，无法进行激活扩散，所以无法翻译出原诗的情景模型。

2 并行FCM算法设计

FCM算法具有计算密集型特点。在地学应用中多用于多图层栅格数据，采用数据并行模式［9］，将数据根据地理范围划分为数据块，分配给不同的进程，各个进程之间协同并行完成聚类任务，达到高效求解的目的。

并行FCM聚类算法的具体步骤如下：

（1）数据并行读取：将数据均衡划分分配成numProcss（进／线程数）份，各进程并行读取数据。

（2）主进程初始化聚类中心，并将聚类中心发送到各子进程中。

（3）各进程按式（3）计算本地模糊隶属度矩阵U，uij为模糊隶属矩阵U中表示第j个元素属于第i个中心的隶属度值。

（4）各进程根据式（5）、式（6），分别求取计算聚类中心（式（4））中分子Num与分母Den：

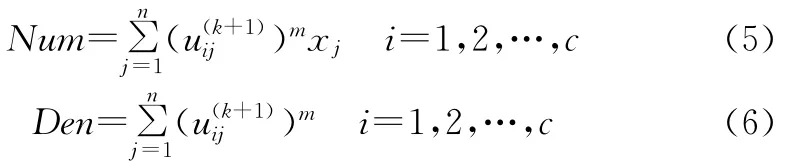
（5）利用全局规约函数AllReduce（），对各进程中分子与分母归并求和，求和结果分别记为Num－Sum和DenSum，然后根据式（7）求解新的聚类中心P（k＋1）：

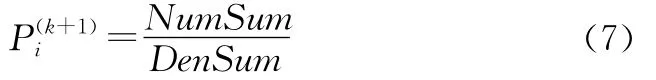
（6）迭代步骤3－5，直到目标函数收敛到设定的阈值。

3 顾及数据划分负载均衡的FCM并行算法

3.1 数据划分中的负载均衡问题

栅格地理数据的并行模式多采用数据并行模式，该模式最基础的是数据划分，传统栅格数据划分主要是按区域大小划分（如按行、列和棋盘划分［9］），该方法较为简单直观，然而由于地理学的研究区不规则，该划分方法将使得分配给各个进程进行计算的数据量不均匀，从而直接导致负载不均衡。图1所示的栅格数据按区域大小均匀划分成3份，由于研究区外的栅格不参与计算，使得各进程的计算量明显不均匀，进程0和进程2的计算量明显小于进程1的计算量（3个进程中计算栅格数百分比分别为20.83%、49.53%、29.64%）。

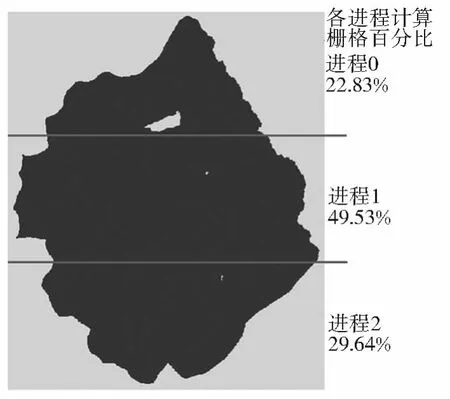
图1 按区域大小划分方式示例Fig.1 Data partition based on size of the area

3.2 按计算强度的数据划分方法

针对上述问题，王少文等提出了按计算强度划分的方法，并将该方法应用于反距离加权插值和空间热点探测［10］。按计算强度划分主要思路是通过构建计算强度估计函数，预测各计算单元的计算量，从而指导数据划分，实现任务负载均衡［10］。该方法首先按式（8）统计栅格数据各行的计算量，然后进行数据划分，使得各进程计算量均匀。

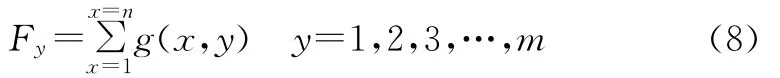
式中：Fy表示栅格数据第y行的计算量，m、n分别表示栅格数据的行数和列数，g（x，y）表示像元（x，y）的计算强度。

记F为计算量Fy组成的数组（数组中元素个数为m），这样按计算强度的数据划分就抽象成如下问题：对数组F进行连续划分，使得各块元素之和中最大值最小。对于该问题，通常采用模拟退火［12］、遗传算法［13］和蚁群算法［14］的方法寻找全局最优解，然而对于现在CPU的强大计算能力，最优解相对于次优解对并行效率的提高并不明显，且模拟退火、遗传算法和蚁群算法相对复杂，故本文以下介绍一种相对简单的求解次优解的方法对数据进行划分。

3.3 按计算强度进行数据划分的并行FCM算法设计

本文采用按计算强度划分数据的方式来解决FCM并行算法中的任务负载不均衡问题。由于FCM算法中每一个研究区栅格像元的计算量一样，研究区外栅格像元不参与计算，因此，本文给出较为简单的计算强度估计函数：

在此基础上，选择一种相对简单的求次优解的方法划分栅格数据。假设将数据划分成K分，则只需要进行K－1次划分，每一次划分都尽量保证是对所要划分的数据进行均匀划分，即找出每一次划分的位置tu（u＝1，2，3，…，K－1），使得式（10）的值最小。数组划分示意图如图2。

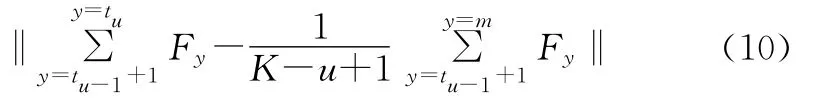
式中：u表示第u次划分（u＝1，2，3，…，K－1），tu表示第u次划分的位置，当u＝1时，记tu－1为0。

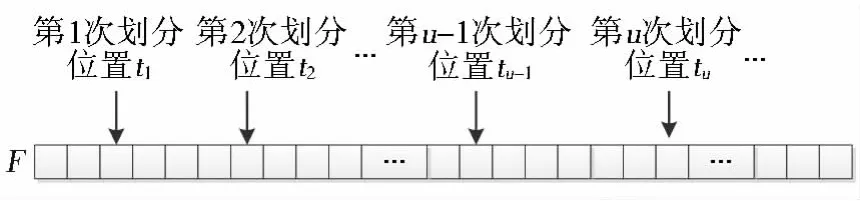
图2 数组划分Fig.2 Array divided

以此方法将图1中栅格数据按计算强度均匀划分成3份（图3），3个数据块中计算栅格数百分比分别为33.33%、33.33%、33.33%，可见按计算强度均匀划分能实现各进程中计算量的负载均衡。

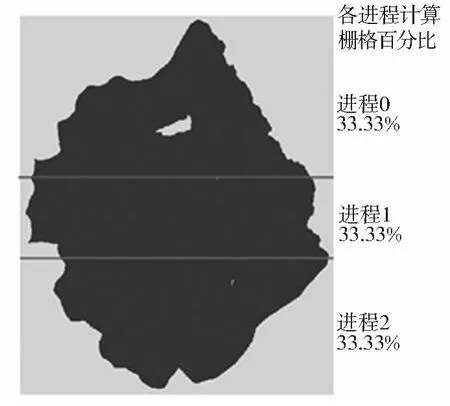
图3 按计算强度划分数据方式示例Fig.3 Data partition based on computational intensity

综上，按计算强度进行数据划分的FCM并行算法流程如图4所示。

4 基于MPI的FCM并行算法实现

目前，并行编程模型主要有基于消息传递（如Message Passing Interface，MPI）和基于共享存储（如OpenMP）两种。当计算节点较多时，基于共享存储编程模型的并行性能远不如消息传递编程模型［15］，因此本文选择基于MPI实现FCM并行算法。上述的FCM并行算法也可基于OpenMP实现。

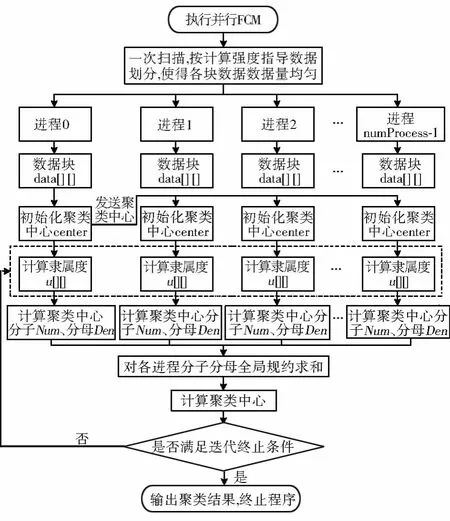
图4 按计算强度划分数据的并行FCM算法流程Fig.4 Flowchart of parallel FCM algorithm

5 应用评价

5.1 研究区数据

本文研究区域位于黑龙江省黑河市嫩江县鹤山农场，面积约60.2km2。数据是由该研究区0.5m分辨率的DEM数据生成的坡度、沿等高线曲率、沿坡面曲率以及地形湿度指数4个环境因子图层数据，每个图层由22 260×18 640个栅格组成，数据格式为.tif，总数据大小为6.4GB。图5中黑色虚线内是研究区。

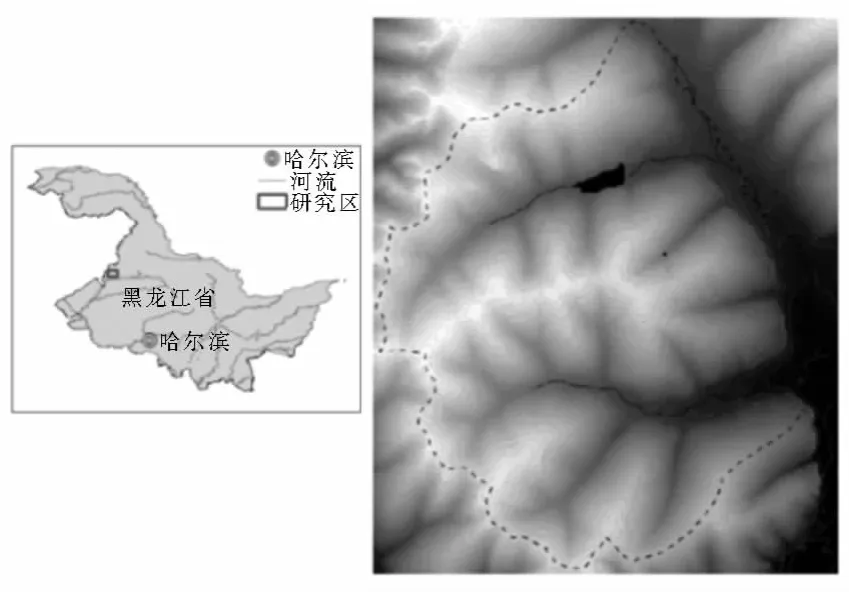
图5 研究区（虚线为研究区边界）Fig.5 Study area

5.2 测试环境及评价指标

本文测试是高性能集群环境，包括4个计算节点和1个存储节点，每个计算节点有两颗Intel（R）Quad Core E5645Xeon（R）CPU，共12核，内存大小为32GB，集群操作系统为Linux CentOS 64位，节点间文件系统为Network File System（NFS）。

本文选取运行时间、加速比、并行效率3种常见的测度指标来表征FCM并行的效果。其中，运行时间仅含计算时间，不包括I／O时间；加速比S即串行算法运行时间T串除以并行算法运行时间T并，如式（11）；并行效率E为加速比S比进程数N，如式（12）。

FCM算法每次都随机选择初始聚类中心，为了具有可靠的对比性，测试时指定算法从相同的初始聚类中心开始迭代，且所有测试迭代次数均相同（本实验为40次）。

5.3 评价结果

FCM的串行算法运行时间为1 130min（约19 h）。如图6所示，两种并行算法均大大缩短了计算时间，按计算强度均匀划分的并行算法比按区域大小均匀划分的并行算法的效率高。随着进程数增加，无论是按区域大小均匀划分还是按计算强度均匀划分，并行算法的运行时间开始都明显减少，随后趋于稳定。当进程数为48h，按区域大小均匀划分和按计算强度均匀划分的并行算法运行时间分别减少到41min（约为串行算法的1／28）和28min（约为串行算法的1／40），表明并行算法实现了该问题的快速、高效求解。

按区域大小均匀划分的并行算法性能明显不如按计算强度均匀划分的并行算法（图7）。从加速比（图7a）看，按区域大小均匀划分和按计算强度均匀划分的并行算法加速比都呈线性增长，然而前者加速比明显低于后者，当进程数为48h，前者加速比只有28左右，后者达到40左右。另外，从并行效率（图7b）看，按区域大小均匀划分和按计算强度均匀划分的并行算法加速效率都呈递减趋势，而后者的并行效率稳定地高于前者（20%以上）。

图6 算法运行时间对比Fig.6 The runtime of algorithm

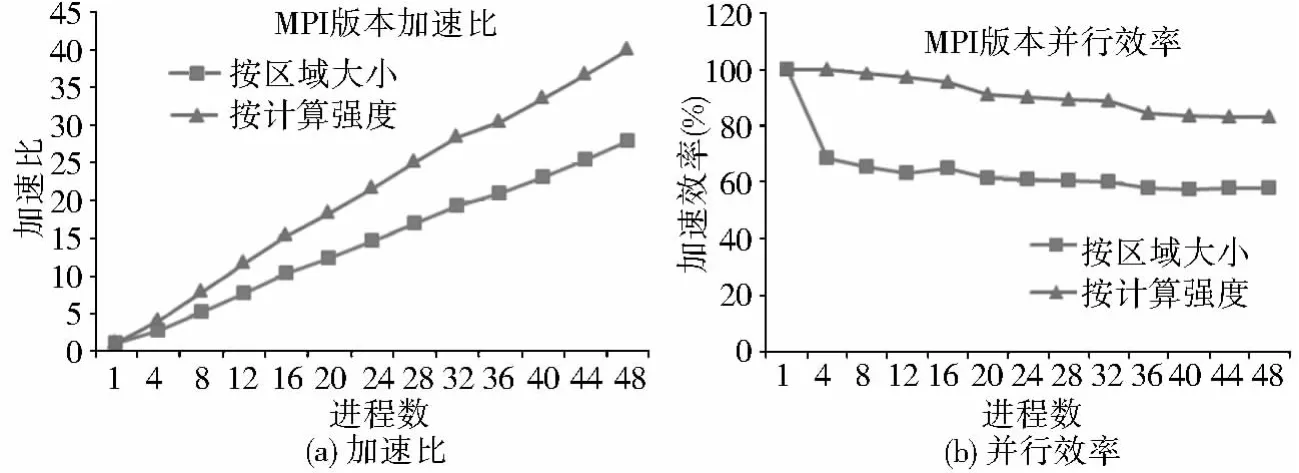
图7 加速比与并行效率Fig.7 The speedup ratio and parallel efficiency

6 结论

本文研究了地理栅格数据FCM算法的并行化，针对并行化时按区域大小均匀划分数据的方式导致的任务（计算量）负载不均衡问题，引入了按计算强度均匀划分的方法，针对全局最优解算法复杂且相对次优解加速效率提高不明显的特点，设计了一种简单求次优解的方法来实现数据划分，并利用MPI实现了并行算法。实验结果表明，所设计的FCM并行方法大大缩短了计算时间，加速性能明显，按计算强度划分的并行算法相较于按区域大小划分的并行算法，加速效率更加明显。本文实现的按计算强度均匀划分的方法适用于研究区域不规则以及数据中存在大量无值区的情况。

［1］ 胡姝婧，胡德勇，赵文吉.基于LSMM和改进的FCM提取城市植被覆盖度——以北京市海淀区为例［J］.生态学报，2010，30（4）：1018－1024.

［2］ 杨琳，朱阿兴，李宝林，等.应用模糊c均值聚类获取土壤制图所需土壤－环境关系知识的方法研究［J］.土壤学报，2007（5）：784－791.

［3］ 邱超.模糊聚类分析在水文预报中的研究及应用［D］.浙江大学，2007.

［4］ 蒋卫国，陈强，郭骥，等.基于HPSO和FCM的多光谱遥感图像湿地分类［J］.光谱学与光谱分析，2010，30（12）：3329－3333.

［5］ KWOK T，SMITH K，LOZAN S，et al.Parallel fuzzy c－means clustering for large data sets［A］.Euro－Par 2002Parallel Processing Proceedings［C］.2002，2400：365－374.

［6］ GONG X J，CI L L，YAO K Z.A FCM algorithm for remotesensing image classification considering spatial relationship and its parallel implementation［C］.2007International Conference on Wavelet Analysis and Pattern Recognition，2007.994－998.

［7］ PETCU D，ZAHARIE D，PANICA S，et al.Fuzzy clustering of large satellite images using high performance computing［A］.High－Performance Computing in Remote Sensing［C］.2011.

［8］ LIU G，LIANG X，HE X.Graphics processing unit based Fuzzy C－Means clustering segmentation［J］.Computer Science，2012，39（1）：285.

［9］ 王结臣，王豹，胡玮，等.并行空间分析算法研究进展及评述［J］.地理与地理信息科学，2011，27（6）：1－5.

［10］ WANG S W，ARMSTRONG M.A theoretical approach to the use of cyberinfrastructure in geographical analysis［J］.International Journal of Geographical Information Science，2009，23（2）：169－193.

［11］ BEZDEK J C.Pattern Recognition with Fuzzy Objective Function Algorithms［M］.Plenum Press，1981.7－10.

［12］ KIRKPATRICK S，GELATT C D，VECCHI M P.Optimization by simulated annealing［J］.Science，1983，220（4598）：671－680.

［13］ LORIES G.Toward a practice of autonomous systems：Proceedings of the first European conference on Artificial life［J］.Behavioural Processes，1996，37（2－3）：257－258.

［14］ DORIGO M，MANIEZZO V，COLORNI A.Ant system：Optimization by a colony of cooperating agents［J］.Ieee Transactions on Systems Man and Cybernetics Part B－Cybernetics，1996，26（1）：29－41.

［15］ 张林波，迟学斌.并行计算导论［M］.北京：清华大学出版社，2006.3－6.