简单要素模型下的多边形对象叠加并行运算策略研究

张树清，张策，杨典华，张俊岩，潘欣，姜春雷

（1.中国科学院东北地理与农业生态研究所，吉林 长春 130102；2.首都师范大学三维信息获取与应用教育部重点实验室，北京 100048）

0 引言

当前，地理信息系统（GIS）正面临着密集计算和海量数据两大挑战。传统地理信息系统软件中的串行算法由于在处理器、内存以及数据传输方面的瓶颈，难以有效应用，从而极大地限制了地理信息系统的应用。并行计算是高性能计算的重要技术［1］，它通过将计算和数据重新组合形成新的任务集并分配到多个计算单元中，在计算单元并行执行，极大地提高了计算效率，对科学的发展产生了深远的影响。这为推动具有计算与数据密集特征的地理信息科学的创新与发展带来了机遇［2，3］。并行计算的引入不仅极大地提高了GIS计算速度，同时可以重新思考GIS新的表达、管理和分析方法［4］。如何有效地利用并行计算技术已成为当前地理信息系统迫切需要解决的科学问题。

矢量叠加分析（Overlay）是对用户感兴趣区域不同数据层及其所含属性进行空间叠置分析［5］，Overlay属于GIS集合操作，为GIS重要空间分析功能之一［1］。研究GIS矢量叠加数据高效并行算法，解决诸如海量复杂空间图层或动态数据快速计算问题，提高GIS实时分析与动态决策能力，将是十分必要的。然而，目前Overlay的并行，大多基于计算效率低、内存资源消耗大的传统扫描线法。因此有必要以简单要素模型的Overlay为基础，从多边形对象分类特征角度，研究高效的空间划分策略与并行算法。尽管多边形Overlay包含交集、并集和差集等复杂计算，但一般可进一步划分为两类最基本操作：1）点包含，一个对象的一个（或者多个）节点包含于另外一个对象中；2）线穿越（线相交），一个对象的一条边界与另外对象的边界相交［6］。谢忠等［5］给出了详细的线穿越（线相交）计算公式以及交点方向判别方法，有关“点包含”检测方法也有较深入研究，常见的方法为射线法［7］。然而，这两种类型只能处理拓扑类型overlapping（部分重叠）及contain（完全包含）或contained by（完全被包含）情形，却无法计算共线相邻（adjacent）或共线包含（cover）或共线被包含（covered by）拓扑类型。事实上，多边形Overlay的另一基本操作类型：“共线”（一个主多边形和叠加多边形有部分相同边界的情形）需要深入研究。为此，本文以多边形交集计算为例，深入研究了共线计算方法，并给出多重数据包围盒（Box）的对象空间划分、筛选与并行计算策略。

1 交集边界共线情形处理

如图1，设交点为P，线段PiPi＋1相对方程为：

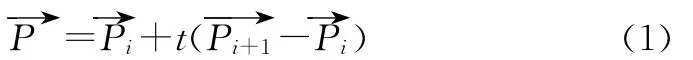
其中：t为点在线段P0Pi＋1中的相对位置，P0为多边形第一个节点：

其中：t为双精度数值，整数部分是节点编号，小数部分是交点在线段P0Pi＋1中的相对位置：t∈［0，1）。

图1 交点P在节点Pi和Pi＋1中的相对位置Fig.1 Relative position of intersection Pbetween node Piand Pi＋1

共线数据链两端点间交点数量计算：1）若2个交点都满足t≠0，两交点间存储的节点数为两交点的相对位置，先取整，再相减；2）若2个交点中1个位于节点上，两交点间存储的节点数为两交点的相对位置，先相减，再取整；3）若2个交点都位于节点上，两交点的相对位置相减，再减1。

共线性质判断定理：两多边形某一区间共线（不分内、外环），交点在A中后一交点相对位置与前一交点相对位置差（DA）乘以交点在B中后一交点相对位置与前一交点相对位置差（DB），若乘积为正，共线是“交集面积区域”边界线；若乘积为负，共线不是“交集面积区域”边界线，只是两多边形相邻边界线。若共线为“交集面积区域”边界线情形，需进一步链接产生新的交集面积区域多边形，而仅仅为两多边形相邻边界线的情形，无需链接产生新的交集面积区域多边形。

图2显示了两个对象A（灰色，外环节点为Pi，内环节点为Si）和B（白色，节点为Qi）相交的两类情形：1）图2a，共线边界不是交集面积区域边界；2）图2b、图2c，共线边界为“交集面积区域”（斜线填充区域）边界线，其中图2c中B对象含有岛区（岛区节点分别为S0、S1、S2、S3、S4）。为简便起见，图中的交点假定与节点重合，因此可直接用节点参与计算相对位置。下面根据共线性质定理判定：1）图2a：DA＝2－3＝－1；DB＝3－2＝1；DA＊DB＝（－1）＊1＝－1＜0：共线为A、B相邻边界线，不是“交集面积区域”边界线。2）图2b：DA＝5－4＝1；DB＝3－2＝1；DA＊DB＝1＊1＝1＞0：是“交集面积区域”边界线。3）图2c：DA＝2－3＝－1；DB＝1－2＝－1；DA＊DB＝（－1）＊（－1）＝1＞0：“交集面积区域”边界线。

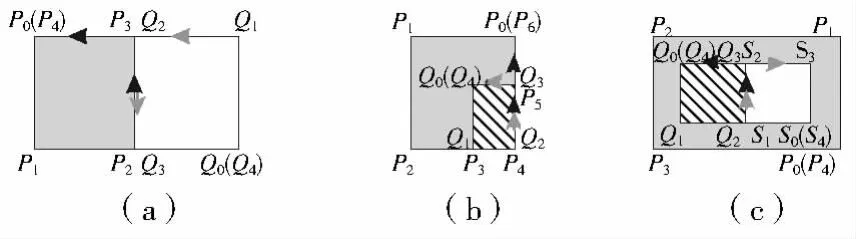
图2 交集区域共线示意Fig.2 Illustration of intersection region collinear

2 多边形对象并行相交逻辑框架

2.1 多层数据包围盒（Box）筛选结构

在数据结构中，无论是二维数据，还是三维数据，都可内部设置一些Box，以减少查询、检索、空间分析时间，而不用进行预处理。既然所有对象数据都是以对象为单位建模的，也就适用于以对象／子对象为单位进行并行计算。现有二维数据，除对象外，无Box。可通过不改变原有数据，附加一文件，提取构造Box，以降低查询时间。

图3给出了多层Box遴选示意图，其中对象A其矩形包围盒为BOX（A），由两个环构成A1和A2，用圆表示，其包围盒分别为BOX（A1）和BOX（A2）；而环A1的边界又可能分为n条链（或段），相应链的包围盒分别为 BOX（A11），BOX（A12），…，BOX（A1n）。同样，对象B包围盒为BOX（B），也由两个环构成B1、B2，包围盒分别为BOX（B1）和 BOX（B2），设B1边界可能分为m条链，其包围盒分别为BOX（B11），BOX（B12），…，BOX（B1m）。这样通过多层Box筛选，可以迅速检索真正相交部分，如与B1相交的A1边界位于BOX（A1i）和BOX（A1j）内。这里“链”（或“段”）指：两交点间（不含其它交点）的多边形连续边界，当无交点存在时，多边形的边界构成一条“闭合链”。

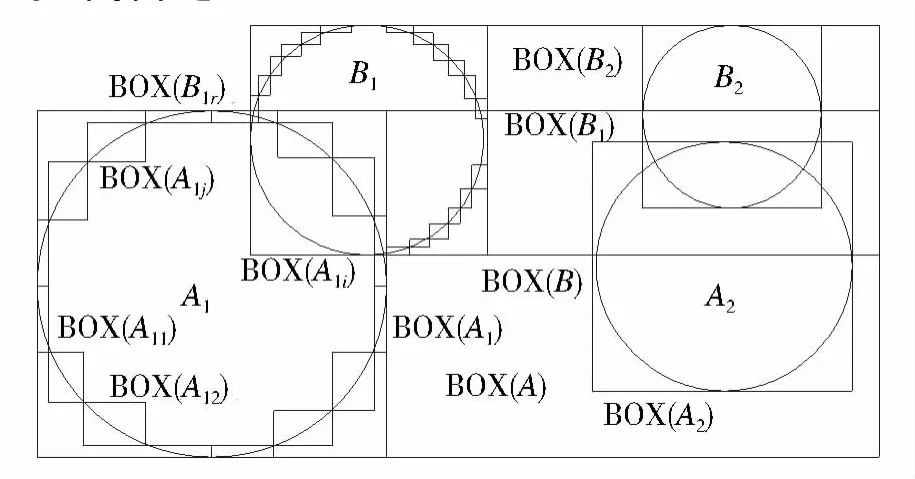
图3 多层数据包围盒空间对象相交示意Fig.3 Illustration of spatial object intersection with multi－level bounding boxes

求交以对象为单位做并行运算。为降低求交时间，划分方法如图4：以吉黑两省土地利用数据（JHLUCC）和土壤数据（JHSOIL）为例，根据报告类型简单对象多的为Ai（i∈［1，n］），不分段；对象少、分为多链的为Bij（i∈［1，u］，j∈［1，v］）（i为对象编号，v为该对象分段数，u为该类对象总数）。据此可建立复杂对象多线程或多进程划分与并行计算模式，故可将u个对象Bij分配在不同计算节点上，各节点单独进行Bij与所有A类对象（Ai（i∈［1，n］））（一对多）的叠加运算（图4）。

图4 复杂对象Overlay多线程或多进程任务划分示意Fig.4 Illustration of multi－thread or multi－processor task partition for complex object Overlay

2.2 多边形分类及其Overlay计算处理流程框架

在简单要素模型中，一般一个多边形对象可包含如下类型：单环 （Single Polygon，SP）、多环（Multi－polygon，MP）；而根据节点数量的多少，每个环又划分为单链（Single Line，SL）或者多链（Multi－Lines，ML）。针对这些不同类型，可分别设置分支处理函数。通过读取主图层和叠加图层数据，可分别统计主图层（A）和叠加图层（B）多边形数据分类情形，并将主要类型设为主体处理函数。这里设定A（单环单链SPSL）对B（单环单链SPSL）为主函数，进入第一层函数，若对象BOX相交，则继续进行“线穿越（线相交）”、“点包含”或“共线”计算，判定多边形是否为边界相交、共线或整体包含。第二层共有四分支函数中：1）当对象A为单环单链（SPSL），对象B为单环多链（SPML），转入该层分支函数1；2）当对象A仍为单环单链（SPSL），对象B为多环（MP），转入该层分支函数2，该函数与主函数的差异在于：对象B中多于一定节点的环要采用BOX筛选；3）当对象A为多链（ML），对象B为一般对象时，转入该层分支函数3，同样需要对多链进行BOX筛选，如此类推；4）当对象A为多环（MP），对象B为一般对象时，转入该层分支函数4。第三层分支函数用于处理第二层分支函数中函数3与4的情况，若对象A为单环多链，对象B为单环或多环时，分别转入该层分支函数1和2；当对象A为多环，对象B为单环时，转入该层分支函数3；当对象A为多环多链，对象B为多环时，转入该层分支函数4（图5），该类处理需要多重BOX筛选（图3）。

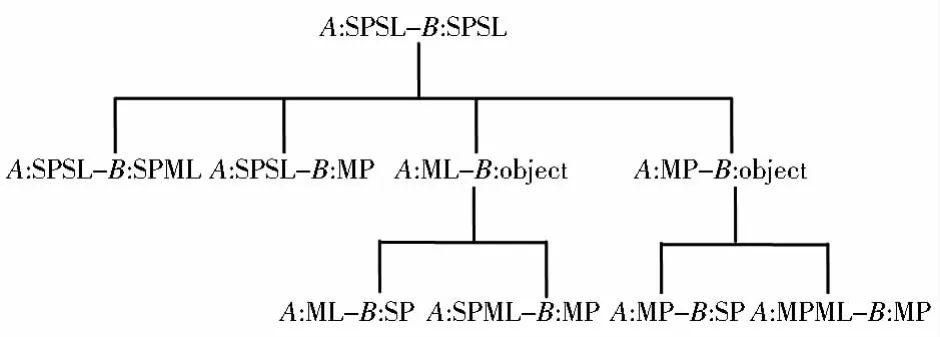
图5 不同类型多边形Overlay分支处理流程Fig.5 Illustration of branch operation for different types of polygon Overlay

3 实验结果与分析

3.1 实验开发环境及数据

处理器：Intel Core 2DuoE7500＠1.6GHz；内存：Ramaxel Technology PC2－6400DDR2 800MHz，2×2GB，800MHz；系统：Microsoft XP，Professional 2002，Service Pack 2；软件：Microsoft Visual Studio 2005C⧺。目前Overlay程序是在单线程下实现，有关多线程或多进程并行程序正在开发中。

采用的数据为：吉黑两省土地利用数据（JHLUCC）和吉黑两省土壤数据（JHSOIL），其数据格式：ESRI Shape。数据量：JHSOIL为47.7MB，JHLUCC为355.0MB；数据类型：JHLUCC中总计对象数量为179 111，其中单环对象数量为172 054，JHSOIL总计对象数量为16 728，单环对象数量为15 439，二者单环数据占绝大多数（大于90%），故可将单环对象求交设为主函数：（单环单链SPSL）对叠加图层（单环单链SPSL）。

3.2 实验结果

以共线情形为例，本文给出了处理结果并验证其准确性。图6是本文软件下两对象共线相交的实例，JHLUCC为主层、JHSOIL为叠加层。其中，图6a为JHLUCC中编号为7667多边形与JHSOIL中编号为394多边形的叠加结果，这里的共线边界为“交集面积区域”边界线；图6b为JHLUCC中编号为93181与JHSOIL中编号为5429的叠加结果，其中的共线边界是两个多边形的邻域边界线，而非“交集面积区域”边界线，说明所给出的算法能够准确处理实际情形。在本文软件下，无论以JHLUCC（对象数量为179 111）为主图层、JHSOIL（对象数量为16 728）为叠加图层，还是以JHSOIL为主图层、JHLUCC为叠加图层，其多边形叠加时间均大约为350s左右。

图6 共线情形实际测试结果Fig.6 Real test result of collinear situation

4 讨论与结论

多边形Overlay是GIS重要分析功能，商业化软件如ArcGIS等其Overlay版本不断升级。然而在学术界对多边形对象叠加的研究却不够系统：首先，已有研究只考虑了“线穿越（线相交）”和“点包含”基本类型［5，6］，对“共线”类型的研究涉足较少，无法处理共线相邻（adjacent）或共线包含（cover）或共线被包含（covered by）拓扑类型，为此，本文提出了共线节点数量的计算方法，以及共线是否为“交集区域边界”的详细判断定理，从而可以有效处理各类空间拓扑关系。其次，多边形对象类型划分及其要素筛选策略的研究不够深入，ESRI shape文件中仅包含对象Box，这仍不能有效地遴选复杂对象（如多环构成的对象）的相交成分。事实上，在构建复杂空间对象过程中应顾及对象与子对象层次关系，而对于由大量节点构成的子对象应考虑子对象数据包围盒，这里的子对象可以是多边形构成的闭合环（如岛），也可以是由两个交点间多边形边界构成的“独立几何单元”，从而提出了面向对象单环、多环、单链、多链特征的多重Box数据筛选及对象空间划分与高效并行运算策略。初步试验表明：该方法具有时间复杂度低、编程简单、内存等资源消耗少等优点。同时，通过有关新增数据包围盒等，可保证与当前数据的兼容性。以吉黑两省土地利用（JHLUCC）和土壤（JHSOIL）ESRI Shape文件数据为例，对以上假定进行初步实验，结果表明，所提出的方法可有效处理任何复杂的共线情形。但限于篇幅，本文仅给出了串行计算实验的初步结果，有关多线程、多进程并行计算以及相关计算效率的比较等有待进一步讨论。

［1］ DING Y M，DENSHAM P J.Spatial strategies for parallel spatial modeling［J］.International Journal of Geographical Information Science，1996，10（6）：669－698.

［2］ WANG S，ARMSTRONG M P.A theoretical approach to the use of cyberinfrastructure in geographical analysis［J］.International Journal of Geographical Information Science，2009，23（2）：169－193.

［3］ WANG S，LIU Y.TeraGrid GIScience gateway：Bridging cyberinfrastructure and GIScience［J］.International Journal of Geographical Information Science，2009，23（5）：631－656.

［4］ DANGERMONJD J，MOREHOUSES S.Trends in hardware for geographic information systems［A］.Proceedings of Auto－Carto 8（Bethesda：American Congress for Surveying and Mapping）［C］.1987.380－385.

［5］ 谢忠，叶梓，吴亮.简单要素模型下多边形叠置分析算法［J］.地理与地理信息科学，2007，23（3）：19－23.

［6］ ZHANG S Q，ZHANG J Y.Theoretical analytics of stereographic projection on 3Dobjects′intersection predicate［J］.International Journal of Geographical Information Science，2010，24（1）：25－46.

［7］ YEHUDA E K.Determining the spatial containment of a point in a general polyhedron［J］.Computer Graphics and Image Processing，1982，19（4）：303－334.