直扩/跳频测控信号伪码跟踪抗干扰性能分析

孟生云 ,杨文革

(1.装甲兵学院,安徽蚌埠 233050;2.装备学院测控工程研究中心,北京 101416)

1 引 言

直扩/跳频混合扩频方式具有直扩的隐蔽性和跳频对干扰的躲避性,技术上更容易获得高扩频增益,载频的跳变增加了信号截获与侦收的难度。在测控系统中引入该扩频技术必能增强系统的抗干扰、抗截获及抗侦收能力。直扩/跳频测控系统已经成为国内新型抗干扰测控系统的研究热点[1]。该类测控系统应用于军用抗干扰测控,故研究该系统的抗干扰性能对系统的设计具有重要意义。其中直扩/跳频测控信号的伪码跟踪直接关系着时延提取的误差精度,影响着测控系统的测距精度,本文研究该类信号在干扰条件下的伪码跟踪性能。

Betz[2]给出了单频干扰下直扩信号伪码跟踪的精度公式,文献[3]推导了存在多普勒频率跳变下的直扩/跳频信号伪码跟踪精度,这些精度误差公式均假定输入干扰服从高斯分布,故其适用范围受到限制。谱分离系数[4]及等效载噪比考察的是相关器输出信号的质量,可反映载波跟踪、捕获和解调性能,不适用于衡量伪码跟踪性能,因为码跟踪是延迟及滞后相关器输出的代数运算,其性能取决于鉴相器函数而不是相关器输出信噪比。Beatrice[5]及刘禹圻[6]借鉴多径对伪码跟踪误差的研究思路,提出干扰误差包络曲线评估干扰对接收机潜在定位性能的影响,其基本思想是以鉴相曲线过零点偏差来表征鉴相函数的失真情况进而反映码跟踪的抗干扰性能,其研究对象为导航系统的直扩信号。

本文首先将直扩/跳频测控信号的码跟踪抗干扰性能分析转化为直扩信号的对应分析,而后推导了伪码跟踪在单音干扰下最大干扰误差,最后通过仿真验证了理论分析的正确性。

2 直扩/跳频测控信号伪码跟踪性能

当干扰频率与本地频点匹配时,干扰才能进入伪码跟踪过程中,否则在接收机前端就被滤掉,因此直扩/跳频测控信号的伪码跟踪过程的输入干扰为时断时续的信号,如图1(a)所示。当某个时隙被干扰,即使干扰能量足以使直扩伪码跟踪失锁,但受到时隙的限制,结果不一定能导致失锁,因为跟踪过程需一定时间来响应干扰的影响或者回到原来锁定状态。由于跟踪过程所需时间以及跳频驻留时间等因素的影响,不易考察干扰时隙内跟踪误差的增加情况和非干扰时隙内跟踪误差的回归情况,难以得到直扩/跳频测控信号的伪码跟踪精度,除非采用环路仿真的方式。

图1 干扰和非干扰时间段示意图Fig.1 Jammed and unjammed intervals diagram

为了便于理论分析,将一个跳频周期内的断续干扰时隙重新排列成连续区域,如图1(b)所示,即假定干扰方获知直扩/跳频测控信号里紧挨着的连续频点,并对这些频点实施干扰。此时信号被分为干扰时间段和非干扰时间段,就干扰对整个跳频周期带来的影响而言,可以对受扰时间段和非受扰时间段的跟踪误差进行加权。设受扰和非受扰时间段内的伪码跟踪稳态误差量分别为 PJ+S和PS,干扰持续时间为TJ,信号周期时间为Tt,直扩/跳频测控信号的一个周期内的平均跟踪误差量P可表示为

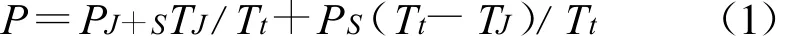
由式(1)可知,信号周期内的跟踪平均误差取决于干扰占用时间段及对应跟踪误差。当干扰总功率一定时,分配的干扰频点越多,信号受扰时间增加,但受扰时间段内的干扰影响减小,因此对干扰方来讲存在一个折衷较优选择,这符合多频点干扰的实际情况。直扩/跳频测控信号的伪码跟踪抗干扰性能分析可以转化为分析受扰时间段内的直扩信号伪码跟踪性能。

3 最大干扰时延误差

音频干扰是一类典型的窄带干扰,且易于建模分析,本节分析在音频干扰下伪码跟踪性能。音频干扰对鉴相器输出S曲线的影响如图2所示。

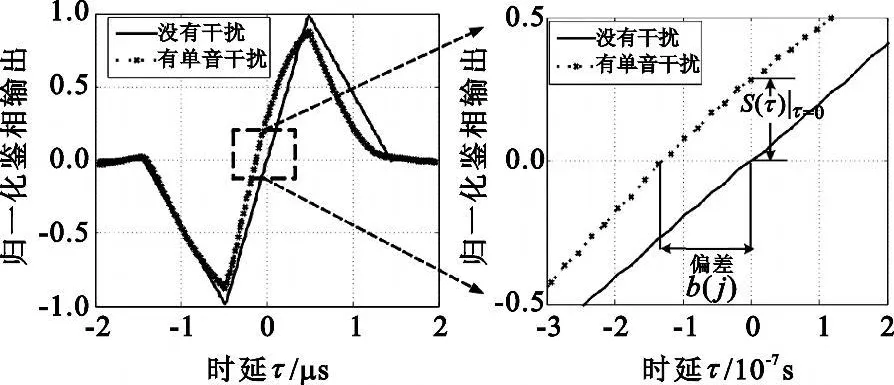
图2 单音干扰下鉴相器曲线示例Fig.2 Phase discriminator curves under single tone jamming

单音干扰一方面改变了S曲线形状发生;另一方面使得曲线过零点发生了偏移,进而在伪码稳定跟踪的结果中引入固定直流分量。干扰最大时延误差(JME)定义为在干扰条件下,鉴相器函数平衡点的最大过零偏差的绝对极值,其移动平均可使JME曲线连续光滑,数学表达式如下:

式中,[J,S]为由干扰及跟踪系统参数组成的参数集, 为参数集[J,S]中的某一变量, τ0为鉴相曲线平衡点 τ0=arg{D(τ,[J,S])=0},D(τ,[J,S])为时延跟踪环的鉴相函数。

采用基带信号形式,伪码跟踪的输入为干扰j(t)与伪码c(t)。非相干超前滞后跟踪方式的原理图如图3所示,同相正交支路结构用复数形式表示。

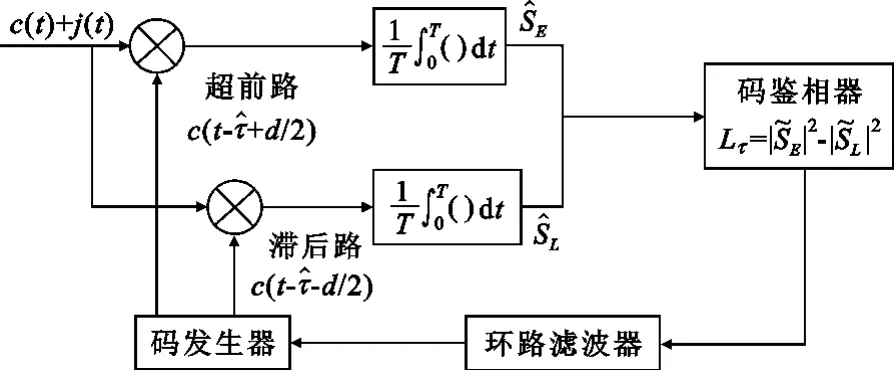
图3 非相干超前滞后码跟踪环原理图Fig.3 Non-coherent early and later code tracking loop diagram

设 SE、 SL为超前及滞后支路的复相关器输出,其鉴别算法为

忽略多普勒频率,令输入信号通过变频至零中频基带信号,可得鉴相曲线函数为

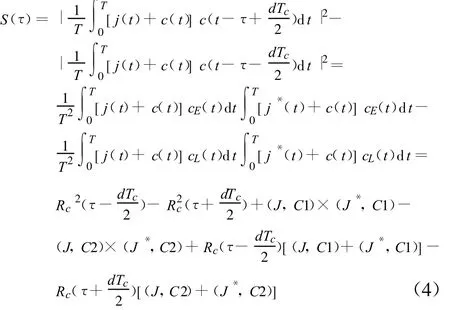
式中,J、J＊分别为干扰及其共轭的幅度谱J(f)、J＊(f)的简写形式,(J,C1)为 J和C1的内积运算:

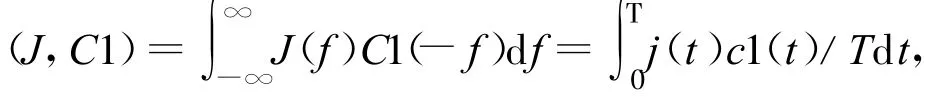
C1和C2分别为超前路和滞后路伪码的频谱。

伪随机码的频谱C(f)可表示为[6]

式中,Sp(f)为码片脉冲赋形的频谱,cn为伪码序列,对于BPSK调制的伪码波形,其码片脉冲频谱为Sp(f)=Tcsinc(πfTc),同时考虑到线状谱特性,取频率fk=k/T,则

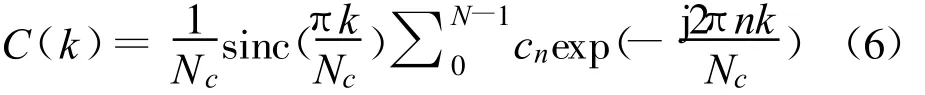
不考虑接收机前端带宽,可精确得到音频干扰下鉴相曲线最大过零偏移。单音干扰的基带形式为复数形式,其时频域分别为

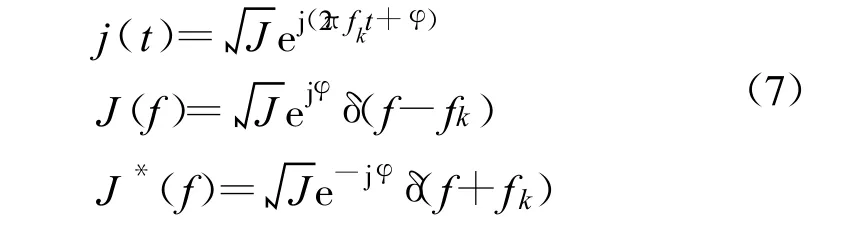
已知信号具有单位功率,则J为干信比,fk为单音干扰相对于与信号中心频率的偏差,φ为单音干扰的相位。

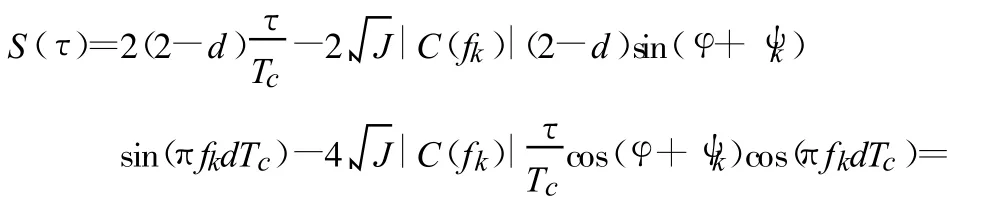
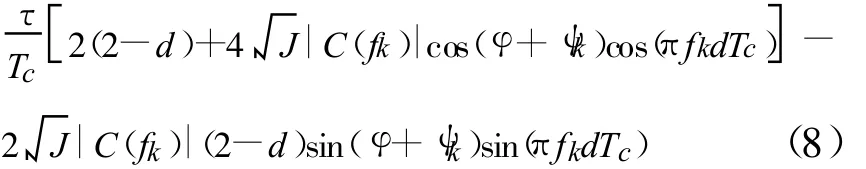
鉴相曲线过零点对应的时延值为

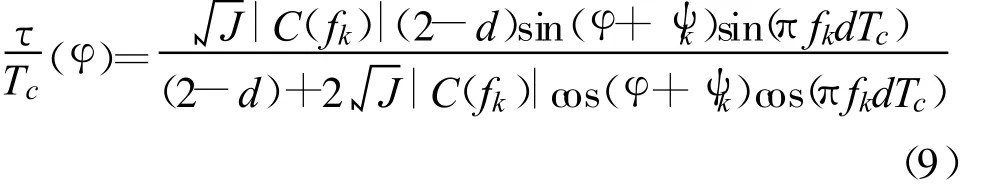
式(9)的最大值在 d(τ/Tc)/dφ=0时取得,经过求导数运算,干扰最大时延误差为

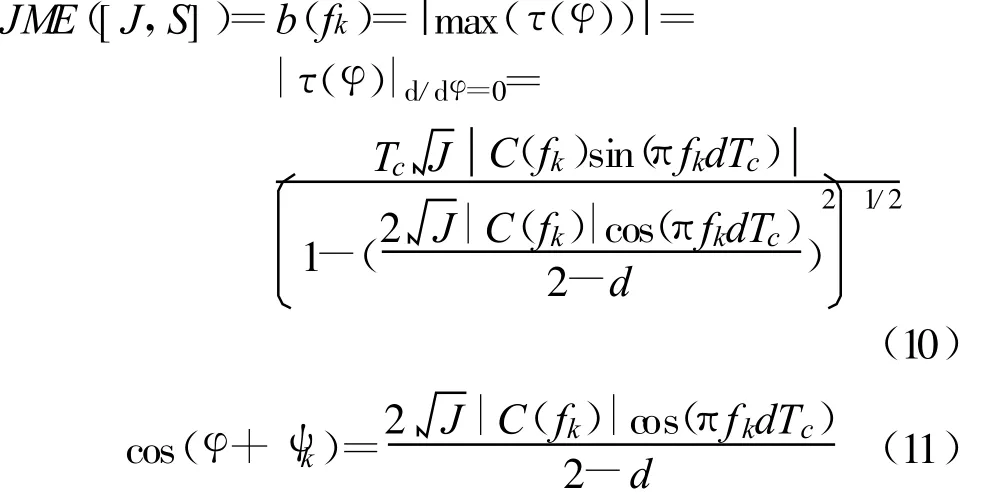
可见,最大干扰误差与相关器间隔d、伪码幅度谱C(fk)、干信比以及干扰频率fk有关。JME随干信比的增加而增加,随音频干扰的频偏变化而变化,变化的包络与伪码频谱相似。当 fk=0.5/(dTc)时,JME最大;当 fk为1/(dTc)的整数倍时,JME为零。式(11)说明J< 20 lg( C(fk)cos(πfkdTc) ) ,即干信比应小于某个数值,否则干扰最大时延误差反映不了干扰的影响。

4 仿真分析

仿真参数如表1所示,仿真中没有加入噪声,只考察音频干扰带来的影响,这里的干扰频差或频率是指干扰与信号中心频率的差值。为便于仿真,伪码码长的设置小于实际测控中伪码码长,但不影响仿真结论。由式(10)得到单音干扰对应的最大干扰误差的理论结果,计算和仿真结果如图4所示。可见,理论计算与仿真结果吻合较好,JME在干扰频率等于半个码率时达到最大,在码率的整数倍处取零值。

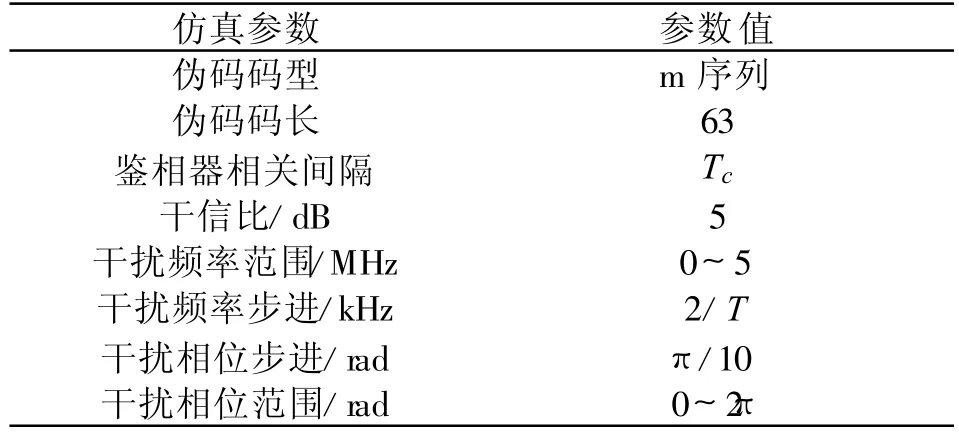
表1 单音干扰最大时延误差仿真参数Table 1 JME simulation parameters under single tone jamming

图4 JME随干扰频率的变化曲线Fig.4 JMEs vs.tone jamming frequency

图5给出了JME随单音干扰的频率和相位的变化情况,其中移动平均表示为

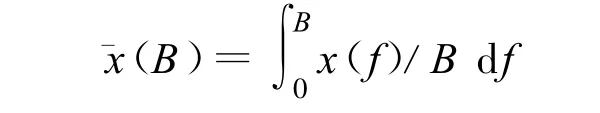
没有考虑伪码的线谱特性而限制干扰频率fk=k/T,但并不妨碍得出结论,干扰频率步进为1 kHz。可见,特定干扰导致的跟踪偏差是可以度量的,通过遍历单音干扰的相位得到伪码跟踪的干扰最大误差。

图5 单音干扰下鉴相曲线过零点偏差及JMEFig.5 Zero value shift and JME under single tone jamming

图6给出了不同信号参数下JME与干信比间的关系,其中干扰频率取0.5Rc。由图(a)知,JME随码长的增加而减小,相同JME值对应的干信比随码长的增加而增加;当干信比超过一定值时,干扰引起的鉴相曲线最大偏差均超过0.4码片,预示环路已经不能有效跟踪码相位。由图6(b)知,JME不随码率的变化而变化。式(10)表明归一化JME与伪码谱形状有关,码长可改变谱主瓣的陡峭形态,而码率不能改变谱主瓣的陡峭形态,因此,在无噪声情况下,JME随信号码长的变化而变化,而不受码率的影响。

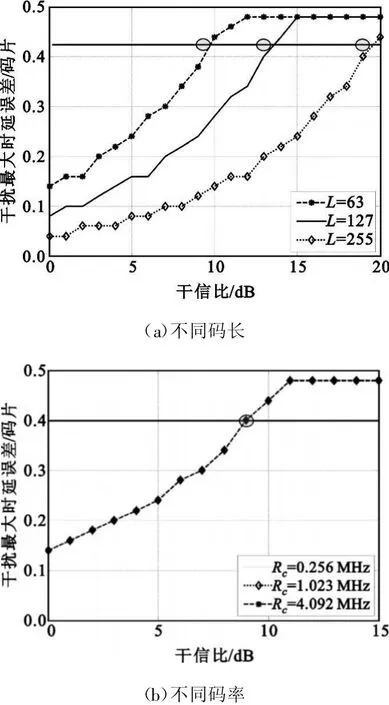
图6 伪码跟踪 JME vs干信比Fig.6 Code tracking JMEs vs.JSR

上面对干扰跳频时隙内的伪码跟踪性能进行了研究,对直扩/跳频测控信号周期内的伪码跟踪平均效果可根据式(1)得到。干扰总功率一定,并在多个干扰信道内平均分配,信号跳频点数12,当干扰信道数为 1、4、8、12时,直扩/跳频测控信号的干扰最大误差如图7所示。可见,干扰信道数较少时,虽干扰时隙内的伪码跟踪误差较大,但干扰对直扩/跳频信号周期内的伪码跟踪影响一般;干扰信道数较多时,干扰时隙内的伪码跟踪误差小,平均效果也一般,而当干扰信道数为4时,伪码跟踪误差达到最大。因此,直扩/跳频测控信号通过增加跳频点数,增加跳频图案的抗截获和抗侦收能力,可提高信号伪码跟踪抗干扰性能。

图7 直扩/跳频测控信号的JME随干扰信道数的变化关系Fig.7 DS/FH TT&C signals JME vs.tone jamming number

综合上述仿真可得如下结论:

(1)伪码跟踪的干扰最大误差的理论分析和仿真结果一致,从而验证了伪码跟踪误差分析的正确性;

(2)在音频干扰的频率距离信号中心频率约半个码片时,干扰对伪码跟踪性能的影响最坏;同时在无噪声情况下,归一化误差JME随码长增加而降低,而不受码率的影响;当干扰功率过大,例如干信比接近扩频增益时,伪码跟踪的干扰最大误差接近半个码片宽度,表明码相位将失去有效跟踪;

(3)通过增加跳频点数或提高跳频图案的抗截获性能,可提高直扩/跳频测控信号的伪码跟踪抗干扰性能。

5 结束语

对直扩/跳频测控信号的伪码跟踪抗干扰性能进行了研究。为便于理论分析,将一周期内的信号分为干扰和非干扰时段,干扰时间段的分析可等效为分析干扰对直扩信号的影响。推导了干扰条件下鉴相曲线过零点偏移极值,即伪码跟踪的最大干扰误差,并得到音频干扰对伪码跟踪的影响规律。理论分析和仿真验证结果相一致,验证了理论分析的正确性。本文工作及所得结论对扩频测控信号的抗干扰性能分析具有一定的参考价值。

[1] 杨文革,孟生云,王金宝.DS/FH扩频测控信号的一种同步方案分析[J].电讯技术,2009,49(6):5-9.YANG wen-ge,MENG Sheng-yun,W ANG Jin-bao.Analysis of a synchronization scheme for DS/FH TT&C signals[J].Telecommunication Engineering,2009,49(6):5-9.(in Chinese)

[2] Betz JW,KolodziejskiK R.Generalized theory of code tacking with an early late discriminator part II:noncoherent processing and numerical results[J].IEEE Transactions on Aerospace and Electronic System,2009,45(4):1551-1564.

[3] Meng Shengyun,Yang Wenge,Lu Weitao,et al.Code tracking performance of DS/FH spread spectrum signal for TT&C[C]//Proceedings of the 2nd IEEE International Conference on Information Management and Engineering.Chengdu:IEEE,2010:491-495.

[4] Hang R Y,Liu Yuqi,Hu Xiulin,et al.Evaluation intersystem interference between compass andGalileo[J].Journal of Convergence Information Technology,2011,6(6):288-299.

[5] Beatrice M,Simone S,Davide M,et al.method for assessing the interference impact on GNSS receivers[J].IEEE Transactions on Aerospace and Electronic System,2011,47(2):1416-1431.

[7] 刘禹圻,胡修林,冉一航,等.卫星导航信号抗单频干扰性能研究[J].电子学报,2011,39(6):1410-1416.LIU Yu-qi,HU Xiu-lin,RAN Yi-hang,et al.Study on evaluating the impact of GWI on DLL tracking performance for GNSS signal[J].Acta Eletronica Sinica,2011,39(6):1410-1416.(in Chinese)