色噪声激励的时滞非线性系统瞬态响应研究

戚鲁媛，徐 伟，高维廷

QI Luyuan1,XU Wei1,GAO Weiting2

1.西北工业大学 理学院应用数学系，西安 710129

2.西北工业大学，电子信息学院，西安 710129

◎博士论坛◎

色噪声激励的时滞非线性系统瞬态响应研究

戚鲁媛1，徐 伟1，高维廷2

QI Luyuan1,XU Wei1,GAO Weiting2

1.西北工业大学 理学院应用数学系，西安 710129

2.西北工业大学，电子信息学院，西安 710129

建立了色噪声与时滞联合作用的非线性系统模型，提出求解其瞬态概率密度的高效近似算法。利用等价变换将时滞系统简化为非时滞系统；通过线性化方法和随机平均原理得到原系统振幅过程的平均Itô随机微分方程和相应的Fokker-Planck-Kolmogorov（FPK）方程。基于退化线性系统导出一组正交基，在该基空间内进行Galerkin变分得到近似瞬态概率密度。将该方法应用到受色噪声激励的双时滞Duffing-Van Der Pol振子得到理论解，采用蒙特卡罗模拟（MCS）验证理论解的正确性。分析了色噪声参数和时滞参数对瞬态响应的影响。研究结果表明：所提理论方法可有效求解受色噪声激励的时滞非线性系统的瞬态概率密度；算法求解效率高于MCS；色噪声和时滞均明显影响了系统瞬态响应。

时滞；色噪声；FPK方程；瞬态概率密度；Galerkin算法

1 引言

不确定因素广泛存在于图像处理、自动化、移动通信、地球物理等研究领域[1-3]。理论上对不确定因素的描述主要分为两类：一是将系统描述为不确定参数系统；二是利用各种噪声对系统进行扰动。研究证明几乎所有的机械（结构）系统都具有一定程度的非线性性态，非线性随机系统的响应预测已然成为理论研究和工程实践的热点问题[4]。众多学者经过长期努力，发展了一系列预测系统响应的理论方法，其中Fokker-Planck-Kolmogorov（FPK）方程方法是扩散过程理论的主要方法。通过求解FPK方程得到稳（瞬）态转移概率密度，可用以分析系统控制[5]、信息熵[6]等实际问题。由于FPK方程的复杂性，其瞬态精确解只能对少数一阶系统得到[7]，一般意义的非线性系统的瞬态解只能结合理论分析与数值计算进行近似求解。

随机平均原理是扩散理论与确定性非线性振动理论相结合的产物，是研究随机非线性系统响应问题的重要理论方法之一。利用随机平均原理可有效避免非白噪声带来的FPK方程扩维现象，并可降低FPK方程维数，简化了理论分析和数值计算。Galerkin法是一种求解微分方程的变分法，1968年，Bhandari和Sherrer首次将Galerkin法应用到求解FPK方程中，得到了稳态概率密度[8]。继而Wen应用其求解了FPK方程的瞬态概率密度[9]。2007年，Spanos结合随机平均理论和Galerkin法研究了白噪声激励的非线性系统的瞬态概率密度，且求解过程不牵扯摄动原理，适用于含有较大非线性参数的系统[10]。

时滞现象广泛存在于计算机、控制等工程实际领域[11-13]。研究时滞作用对瞬态概率密度的影响具有重要的理论及应用价值，并已经引起相关学者的注意。文献[14]将随机平均原理和Galerkin法两者结合分析了白噪声作用的非线性时滞系统的瞬态概率密度。正如很多学者指出的，实际中存在的噪声是具有一定相关时间的有色噪声，故而研究色噪声对瞬态概率密度的影响是研究此领域不可缺少的一部分。总结前人工作发现，对色噪声激励的非线性系统瞬态概率密度的研究工作较少[15]，研究时滞与色噪声共同作用的非线性系统的瞬态概率密度仍处于空白阶段。

综上所述，本文将等价线性化原理、随机平均理论和Galerkin算法三者结合，求解色噪声与时滞联合作用的非线性振子的瞬态概率密度；系统地分析了该算法的有效性，并研究了色噪声和时滞对系统瞬态概率密度的影响。

2 模型构造

建立色噪声激励的时滞非线性系统模型如下：

ζk(t)为零均值，强度为hk，谱密度函数为Sk(τ)的相互独立的有色噪声。假设存在一个δ小量且H和F是δ阶小量，hk为δ1/2阶小量。

3 理论求解过程

3.1 随机平均原理

对式（1）应用随机平均原理，引入如下变换：

其中，A(t)、Φ(t)、Θ(t)均为随机过程；A(t)和Θ(t)是慢变过程，Φ(t)是快变过程。在小时滞假设下将 Xτi、X˙τi近似展开为如下形式：

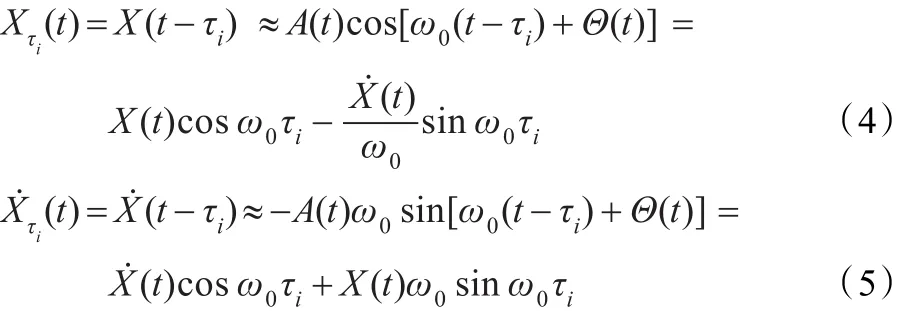
利用式（4）、（5）可将 Xτi和 X˙τi转化为非时滞情形，故而系统（1）等价为如下非时滞系统：

由等价线性化原理，将式（6）变形为如下形式：

由式（3）可得：

由式（3）、（7）、（9）可得：

对式（10）应用随机平均原理[16]，得到A(t)的Itô随机微分方程为：

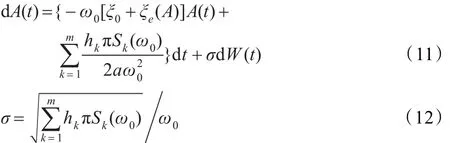
其中，W(t)为单位维纳过程，式（11）对应的FPK方程为：

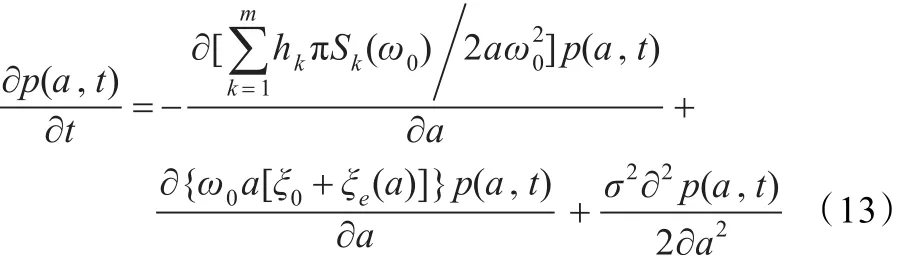
初值问题式（13）、（14）的理论精确解难以得到，下面通过Galerkin算法进行近似求解。

3.2 Galerkin算法原理

首先考虑式（1）的退化线性方程，如下：

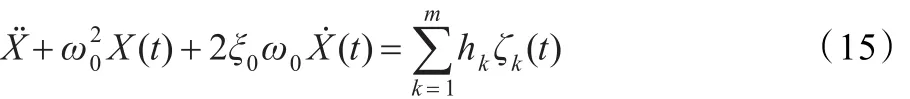
在式（13）中令ξe(a)=0得与式（15）对应的FPK方程：

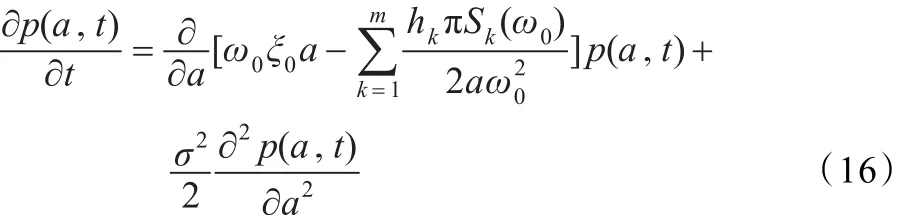
利用变量分离法[17]，得式（16）的特征值与特征函数：

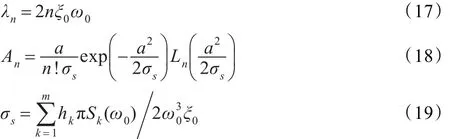
其中，λn表示特征值，An表示正交基函数，σs表示系统（15）中X(t)的平稳方差，Ln(˙)表示n阶Laguerre多项式。

方程（13）的解可近似写成如下形式：

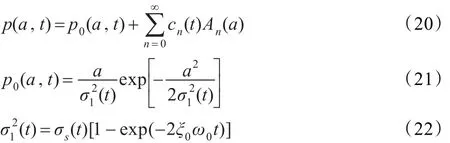
其中，cn(t)是待求解项，p0(a，t)是式（16）的解。表示 p(a，t)相对于 p0(a，t)的偏移程度，此偏移由非线性项和时滞项引起。实际计算中，级数求和形式需进行适当截断(n=0，1，…，N)。

将式（20）代入式（13），并结合FPK方程特征函数定义，得如下误差参量：

以Aj(a)A0(a)为权函数，基于Galerkin方法，令误差参量满足下列条件：

根据Laguerre多项式的性质，推得如下化简关系式：

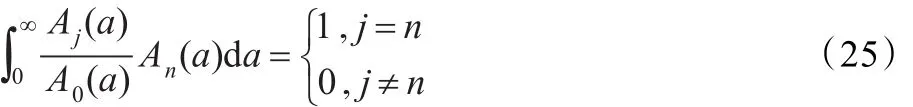
将式（23）代入式（24）并按式（25）进行化简，得到关于cj(t)的方程组，如下：

由式（14）和式（20）可得式（26）的初始条件为：cj(t)=0。将式（26）的解代入式（20）即得瞬态响应概率密度。

4 算例分析

选如下复杂色模型为例进行分析。此模型称为白噪声二阶滤过过程[18]，其数学表达为：其中，常数ϖk和 βk是噪声参数，影响噪声带宽，ϖk和 βk增大代表带宽变宽。Wk(t)是强度为2Dk的高斯白噪声，此过程有如下谱密度：

算例中取非线性项和时滞项为如下形式：

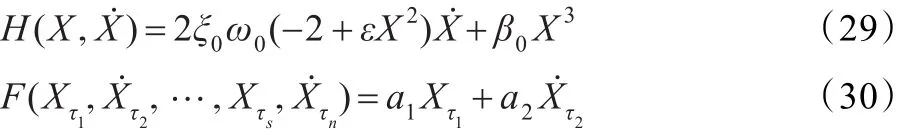
其中，ω0和ξ0与（1）中相同，a1、a2、β0和ε均为常数。算例中取一个色噪声激励的情况(h1=1)。

4.1 理论分析

将式（29）、（30）代入式（1）即得色噪声激励的双时滞Duffing-Van Der Pol振子。

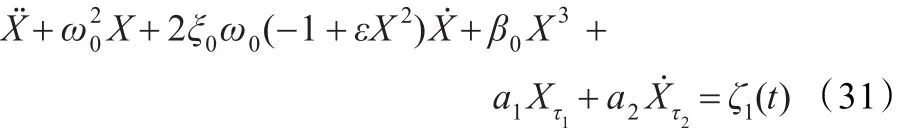
将式（29）、（30）代入式（8）并结合式（4）、（5）可得：

将式（32）代入式（13）得与式（31）相应的FPK方程为：

由式（17）～（19）得特征值和基底函数为：

将式（32）代入式（23）得误差参量为：

由式（18）并结合Laguerre多项式性质得化简关系式：

由式（32）代入式（26）并利用式（39）、（40）化简，最终得到关于cj的方程组如下：

式（41）中，cj(t)下标为负时认为不存在；式（43）中δj，n为Kronecker Delta符号。

4.2 数值分析

本文4.1节已举例对第3章建立的算法进行了理论分析，为说明色噪声参数和时滞参数对 p(a，t)的影响，本节选不同参数值进行数值计算，同时对式（31）进行MCS，将理论解和MCS解对比来验证算法可行性。

图1给出了方程（41）的解(N=8)。系统参数取值为：ω0=1，ξ0=0.02，ε=5，β0=0.5，α1=0.01，α2=0，τ1=τ2=0.5；噪声参数取值为 D1=1，ϖ1=3，β1=0.5。从图中可直观看出，随时间增加，cj(t)将趋向于一系列稳定值，稳定时间约为100 s。

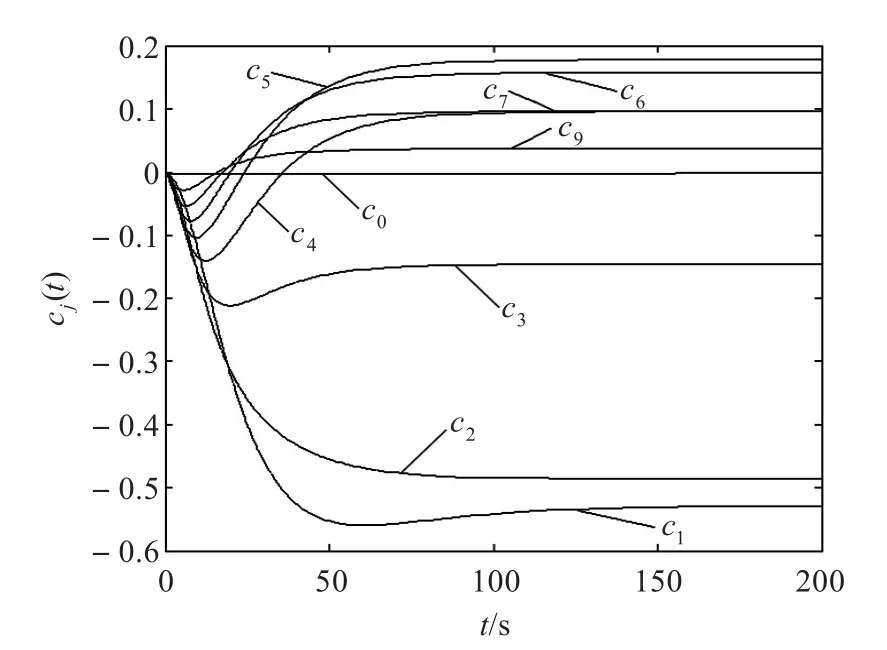
图1 cj(t)的时间演变情况

图2显示了不同时刻振幅概率密度函数 p(a,t) (N=20)，其参数取值与图1中的参数相同。采用Euler算法进行MCS。可以看出，由本文建立的算法得到的理论解和MCS解吻合程度好，这证明了本文建立的算法是有效的。由于系统在100 s后达平稳状态，故该方法在一定程度上刻画了稳态响应，为求解稳态概率密度提供了新途径。

图3为振幅概率密度 p(a，t)(N=20)，ϖ1=3.5，其余参数与图2中的参数相同。可以看出，理论近似解和MCS解拟合程度非常好。比较图2和图3易知，ϖ1对 p(a，t)产生了显著影响，随着ϖ1增大，p(a，t)有一个向左的偏移，在较小幅值处达到峰值。从概率论角度解释为：系统将以更大的概率在更小的幅值运动，增大ϖ1可降低系统响应程度。

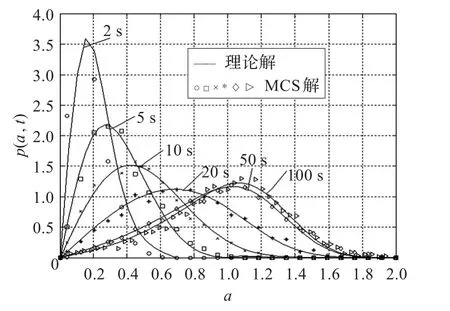
图2 p(a，t)(ω0=1，ξ0=0.02，ε=5，β0=0.5，α1=0.01，α2=0，τ1=τ2=0.5，D1=1，=3，β1=0.5)

图3 p(a，t)(ω0=1，ξ0=0.02，ε=5，β0=0.5，α1=0.01，α2=0，τ1=τ2=0.5，D1=1，=3.5，β1=0.5)

图4为令 β1=1.0其余参数与图2中相同时，p(a，t)图像。比较图2和图4发现，参数β1对 p(a，t)的影响是显著的。增大 β1使 p(a，t)向左偏移，在较小幅值处达到峰值。从概率角度可得如下结论：增大β1可降低系统响应程度。

图4 p(a，t)(ω0=1，ξ0=0.02，ε=5，β0=0.5，α1=0.01，α2=0，τ1=τ2=0.5，D1=1，=3，β1=1)

图5～图7分析了时滞参数对 p(a，t)的影响。参数取值为：ω0=1，ξ0=0.01，ε=2.5，β0=0.5，α1=0.01，α2=0，D1=1，ϖ1=3，β1=0.5。图5中τ1=τ2=0.5，图6中τ1=τ2=1.5，图7中τ1=τ2=4.7。

图5～图7表明以下两点：（1）理论解和MCS解吻合相当一致，证明了本文算法的有效性；（2）对比图5～图7发现，时滞对 p(a，t)产生了影响，影响较为显著。

图5 p(a，t)(ω0=1，ξ0=0.01，ε=2.5，β0=0.5，α1=0.01，α2=0，D1=1，=3，β1=0.5,τ1=τ2=0.5)

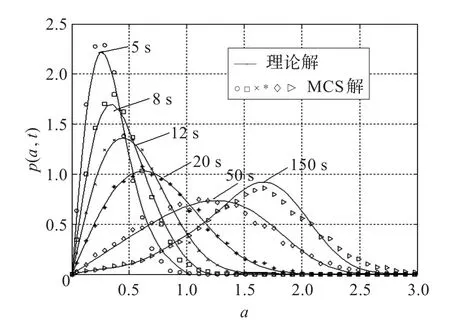
图6 p(a，t)(ω0=1，ξ0=0.01，ε=2.5，β0=0.5，α1=0.01，α2=0，D1=1，=3，β1=0.5,τ1=τ2=1.5)

图7 p(a，t)(ω0=1，ξ0=0.01，ε=2.5，β0=0.5，α1=0.01，α2=0，D1=1，=3，β1=0.5,τ1=τ2=4.7)

综合图2～图6分析，色噪声和时滞均对系统瞬态概率密度 p(a，t)产生了影响，故在研究非线性系统瞬态概率密度时考虑色噪声和时滞的联合作用是非常必要的。数值计算过程中发现，本文算法不但可以有效求解此类方程，且求解效率相对MCS是极高的。以N=15为例，利用本文算法所需计算时间与MCS相比缩减1/12；当N=25时，本文算法耗时为MCS的1/3。

5 结论

建立了色噪声激励的时滞非线性系统模型，并对此模型建立了求解瞬态响应的相关算法。该算法包括三方面：

（1）将时滞方程简化为非时滞方程；

（2）利用等价线性化和随机平均法得到系统振幅的平均Itô随机微分方程和平均FPK方程；

（3）由FPK方程本征函数法得到正交基，进行Galerkin变分并求解相应的常微分方程组得到与时间相关的系数，进而得到瞬态概率密度函数。

以白噪声二阶过滤过程为色噪声模型，以Duffing-Van Der Pol振子为算例实现本文建立的算法。利用MCS对原系统进行模拟，模拟解和理论解对比发现拟合程度非常好，证明本文的近似算法是有效的。通过对色噪声参数和时滞参数的研究发现色噪声和时滞对瞬态概率密度具有显著影响，研究瞬态概率密度时考虑色噪声和时滞的作用是非常必要的。

本文算法可通过观察与时间相关的系数的解，直观看出系统是否具有稳态解，并可估计系统到达稳态的时间，使得利用MCS计算稳态响应时能大大减少盲目运算时间，克服了使用MCS计算稳态响应时耗费时间的问题。该算法是研究随机非线性振动系统瞬态概率密度的一种简便方法，对理论研究及工程应用具有重要意义。

[1]Mohamed W，Hamza A B.Medical image registration using stochastic optimization[J].Opt and Lasers Eng，2010，48：1213-1223.

[2]Liu J，Liu X Z，Xie W C，et al.Stochastic consensus seeking with communication delays[J].Automatic，2011，47：2689-2696.

[3]Repperger D W，Farris K A.Stochastic resonance—a nonlinear control theory interpretation[J].Int J Syst Sci，2010，41：897-907.

[4]Lin Y K，Cai G Q.Probabilistic structural dynamics[M].New York：Mc Graw Hill，2004.

[5]Zhu W Q，Deng M L.Optimal bounded control for minimizing the response of quasi-integraable Hamiltonian systems[J].Non-Lin Mech，2004，39：1535-1546.

[6]Guo P R，Xu W，Liu D.Upper bound for the time derivative of entropy for a stochastic dynamical system with double singularitied driven by non-Gaussian noise[J].Chinese Phys B，2010，19：1-6.

[7]朱位秋.随机振动[M].北京：科学出版社，1992：223-308.

[8]Bhandari R G，Sherrer R E.Random vibrations in discrete nonlinear dynamic systems[J].J Mech Eng Sci，1968，10：168-174.

[9]Wen Y K.Approximate methods for nonlinear random vibration[J].J Eng Mech Div，1975，101：389-401.

[10]Spanos P D，Sofi A，Di Paola M.Nonstationary response envelope probability densities of nonlinear oscillators[J].J of Appl Mech，2007，74：315-324.

[11]Hetel L，Daafouz J，Jungers M.Delay-dependent sampled-data control based on delay estimates[J].Systemsand Control Letters，2011，60：146-150.

[12]Maccari A.Time delay control for two van der pol oscillators[J].J Comput Nonlin Dyn，2011，6：11-16.

[13]Luan B L，Keiji K，Naoyuki H.Design and experimental verification of multiple delay feedback control for time-delay nonlinear oscillators[J].Nonlinear Dynam，2012，67：1407-1418.

[14]Jin X L，Huang Z L.Nonstationary probability densities of strongly nonlinear single-degree-of-freedom oscillators with time delay[J].Nonlinear Dynam，2010，59：195-206.

[15]Qi L Y，Wu W，Gu X D.Nonstationary probability densities of a class of nonlinear system excited by external colored noise[J].Sci China-Phys Mech Astron，2012，55：477-482.

[16]Stratonovich R L.Topics in the theory of random noise，Vols 2[M].New York：Gordon and Breach，1986：170-305.

[17]Gardiner C W.Handbook of stochastic methods for physics，chemistry and the natural science[M].Berlin：Springer-Velarge，1983：154-170.

[18]Feng C S，Wu Y J，Zhu W Q.Response of duffing system with delayed feedback control under combined harmonic and real noise excitations[J].Commun Nonlinear Sci Numer Simulat，2009，14：2542-2550.

1.Department of Applied Mathematics,Northwestern Polytechnical University,Xi'an 710129,China

2.School of Electronic Information,Northwestern Polytechnical University,Xi'an 710129,China

An effective approach to calculate the transient probability densities of the multi-delayed nonlinear system driven by colored noise excitations is developed.The system with time delay is simplified to an equivalent system without time delay.The linearization technique and the stochastic averaging method are adopted to obtain the averaged Itô stochastic differential equation and the corresponding FPK（Fokker-Planck-Kolmogorov）equation for the amplitude process.A set of orthogonal base functions is obtained from the degenerated linear system.The Galerkin method is applied in the orthogonal base space to obtain the approximate probability densities.The proposed procedure is applied to the Duffing-Van Der Pol oscillator with two time delays and an external colored noise.The reliability of the theoretical results is verified by MCS（Monte Carlo simulation）.Effects of the colored noise and the time delay are also discussed.The results show that the proposed method is effective at studying the transient probability densities of the time-delayed nonlinear system driven by colored noises;the theoretical calculation efficiency is higher than that of MCS;both of the colored noises and time delay affect the transient responses.

time delay;colored noise;FPK（Fokker-Planck-Kolmogorov）equation;transient probability density;Galerkin method

A

TP301.5

10.3778/j.issn.1002-8331.1210-0061

QI Luyuan,XU Wei,GAO Weiting.Study on transient probability densities of delayed nonlinear system excited by colored noises.Computer Engineering and Applications,2013,49（7）：1-5.

国家自然科学基金（No.11172233，No.10932009，No.61171155）；陕西省自然科学基金（No.2012JM8010）；西北工业大学博士论文创新基金（No.CX201215）。

戚鲁媛（1986—），女，博士研究生，研究领域为应用数学，非线性随机振动；徐伟（1957—），男，博士，教授，博士生导师，研究方向为应用数学；高维廷（1984—），男，博士研究生，研究方向为通信信号处理。E-mail：qiluyuan@gmail.com

2012-10-09

2012-12-18

1002-8331（2013）07-0001-05

CNKI出版日期：2012-12-26 http://www.cnki.net/kcms/detail/11.2127.TP.20121226.1120.001.html