基于PSO-BP的软件缺陷预测模型

于安雷，皮德常

基于PSO-BP的软件缺陷预测模型

于安雷，皮德常

软件缺陷检测旨在自动检测程序模块中是否包含缺陷，从而加速软件测试过程，提高软件系统的质量。针对传统软件缺陷预测模型被限制在一定的应用范围而影响其预测的准确性和适用性，提出了一种基于PSO-BP软件缺陷预测模型。该模型运用粒子群优化算法优化BP神经网络的权值和阈值，采用交叉验证的方式进行实验，并与传统的机器学习方法J48和BP神经网络等方法进行了比较。实验结果表明提出的方法具有较高的预测准确性。

软件缺陷预测；神经网络；粒子群优化

1 引言

随着软件系统在工程应用中不断扩大，软件缺陷[1]的危害越来越受到人们的关注。例如，1962年，因Fortran语言少写一个连字符，美国国家航天局（NASA）不得不销毁价值8 000万美元的马里纳1号探测器[2]。软件缺陷预测能够在软件开发的早期预测出哪些模块有出错的倾向从而尽早改正缺陷模块，对于提高软件可靠性有着重要的意义。本文提出的预测技术是一种静态预测技术，即基于缺陷相关的度量数据，对缺陷分布进行预测的技术。

目前，软件缺陷预测模型主要包括Bayesian模型[3]、线性判别模型（Linear Discriminant Analysis，LDA）、支持向量机模型（Support Vector Machine，SVM）[4]、分类回归树模型（Classification and Regression Tree，CART）、马尔可夫模型等。但这些方法尚存在一些问题，例如，Bayesian模型在因子过多，模型结构较为复杂的情况下，计算效率和推理过程缓慢不易被人接受；分类回归模型泛化能力比较差；支持向量机参数选择缺乏有效的方法；马尔可夫模型需要提出很多假设，在实际应用中受到许多限制。

J48是一种决策树算法，严格意义上说是一种对ID3算法的改进[5]。通过信息增益率选择属性避免了偏向属性值高的弊端；在建树的过程中不断剪枝；能够对不完整数据进行处理以及连续属性值的离散化处理；但是在构造树的过程中需要对数据集进行多次的顺序扫描和排序，导致算法低效。

人工神经网络模型[6]（ANN）起源于对生物系统的研究和模仿，目前，在软件缺陷预测中主要应用的神经网络是BP神经网络。但神经网络容易陷入局部极小值点，收敛速度慢等缺点。粒子群优化算法[7]（PSO）由Kennedy和Eberhart于1995年共同提出，具有算法简单，不需要设置参数，以及不要求目标函数可导、可微，甚至不要求有明显的表达式等优点。

为了提高软件模块缺陷预测模型的准确性，本文提出了基于PSO-BP的软件缺陷预测模型，即运用粒子群优化算法优化BP神经网络的权值和阈值，建立软件缺陷预测模型，最后用于实验预测软件模块是否为缺陷模块。

2 相关工作

2.1 神经网络

人工神经网络以数学和物理方法以及从信息处理的角度对人脑神经进行抽象，并建立简化模型，模拟人脑的智能处理行为[6]。BP神经网络是一种误差反传神经网络，是一种有监督的学习方法。其基本思想是：神经网络在外界样本的刺激下反向传播算法不断地动态修整网络的连接权值和阈值，以使网络的输出等同期望或者以设定的误差接近期望输出[8]。曾有研究表明三层网络可较好地解决非线性映射、优化设计等问题[9]。因此本文基于这一成果，选用三层神经网络，即包括输入层、隐藏层、输出层。本文定义的误差平方计算如公式（1）：

其中，m为输出向量的维数，Yi，k是样本i的第k维期望输出值，Oi，k是样本i的第k维实际输出值，Ei为样本i网络误差的平方。

2.2 粒子群优化算法

粒子群优化算法思想起源于对鸟群觅食和人类作决策时的行为模型的研究，它是一种基于群智能的随机全局优化算法[10]。与遗传算法相比，它避开了遗传算法固有的选择、交叉及变异等操作，根据自己速度进行搜索，缩短了神经网络的训练时间，加快了收敛速度。因此本文采用粒子群优化神经网络，达到提高神经网络的泛化能力。

粒子群优化算法首先在目标函数空间中生成初始种群，即随机初始化粒子的位置及速度，每一个粒子的位置都是目标函数的一个可行解，并有目标函数确定其适应值。本文的适应值由式（2）确定：

其中，n为样本的数量，Ei由式计算，Fpindex为粒子的适应度，pindex的取值为 pindex=1，2，…，size，size为粒子群规模。

在粒子群优化过程中，粒子的速度和位置按如下公式（3）、（4）进行调整：

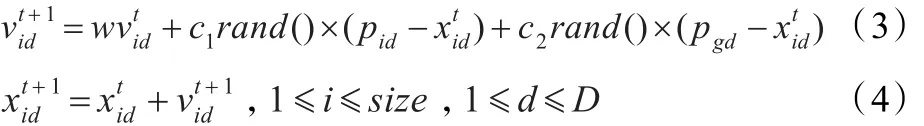
其中，D为粒子的速度与位置的向量维数，t为当前的迭代次数，w为惯性权重，c1和c2为加速常数，rand（）为随机产生整数，pid为粒子i的当前最优位置的第d维分量，pgd为当前种群最优位置的第d维分量，为第t次迭代时，粒子i位置向量的第d维分量，为第t+1次迭代时，粒子i速度向量的第d维分量。

3 软件缺陷预测模型的建立

3.1 软件缺陷预测模型

基于PSO-BP方法的软件缺陷预测模型主要包括如下几个步骤，如图1所示。

建立软件缺陷预测模型主要步骤如下：

（1）获取软件缺陷数据集。

（2）基于训练样本建立BP神经网络的软件缺陷预测模型，选择sigmoid转移函数，采用三层网络结构。

（3）利用PSO算法优化BP网络的权值和阈值。

（4）用测试样例对模型进行分类预测。如果预测结果满足终止条件，则停止优化得到优化的软件预测模型；否则返回步骤3，继续优化模型。

其中，终止条件为模型的预测准确率达到事先设定的阈值或者循环次数达到事先设定的最大值。

图1 软件缺陷预测模型图

3.2 PSO优化BP神经网络

因为BP神经网络中的误差梯度下降法，要求其函数可微、可导，本文采用PSO优化BP神经网络的权值和阈值，以达到改进BP算法的缺陷和提高泛化性能的目的。即运用粒子群优化算法计算出每个粒子在每个方向上的速度和位置映射到BP神经网络的权值和阈值。每个粒子在个体经验和群体经验指导下寻找自身最优解和群体最优解的步骤如下：

（1）初始化粒子群。

（1.1）设定粒子群规模大小，粒子速度和位置以及向量的维数，其中，本文粒子规模为30，向量的维数与BP神经网络的权值和阈值的个数之和相等；

（1.2）随机初始化每个粒子的位置及速度以及个体最优解和群体最优解；

（1.3）根据经验，设定惯性权重w为0.3，加速常数c1和c2为2，设定最大进化代数Tmax。

（2）将粒子的速度和位置分量映射给BP神经网络，按照公式计算每个粒子的适应度。

（3）按照如下式进行适应度的比较：

如果current＜pbestfit，则pbestfit=current，pbest=xi；否则gbest和pbestfit不变。

如果current＜gbestfit，则gbestfit=current，gbest=xi；否则gbest和gbestfit不变。

其中，current是粒子的当前适应值，pbestfit是粒子的个体最优值，gbestfit是种群全局最优适应值，pbest是粒子个体最优值，gbest是种群全局最优值，xi为粒子当前位置。

（4）根据式（3）和式（4）更新粒子的速度和位置，通常为让粒子达到最佳全局寻优能力，设置速度阈值Vmax，做如下限制：

（5）将迭代次数与Tmax进行比较，如果大于Tmax，则终止算法，且当前的gbest为BP神经网络优化的权值和阈值；否则跳至步骤2，继续下一次迭代。

4 实验分析

4.1 实验数据

本文采用的实验数据是由NASA提供的数据包[11]，其中含有13个数据集，如表1所示。这些数据集都是NASA的真实软件项目，由常见的开发语言编写。

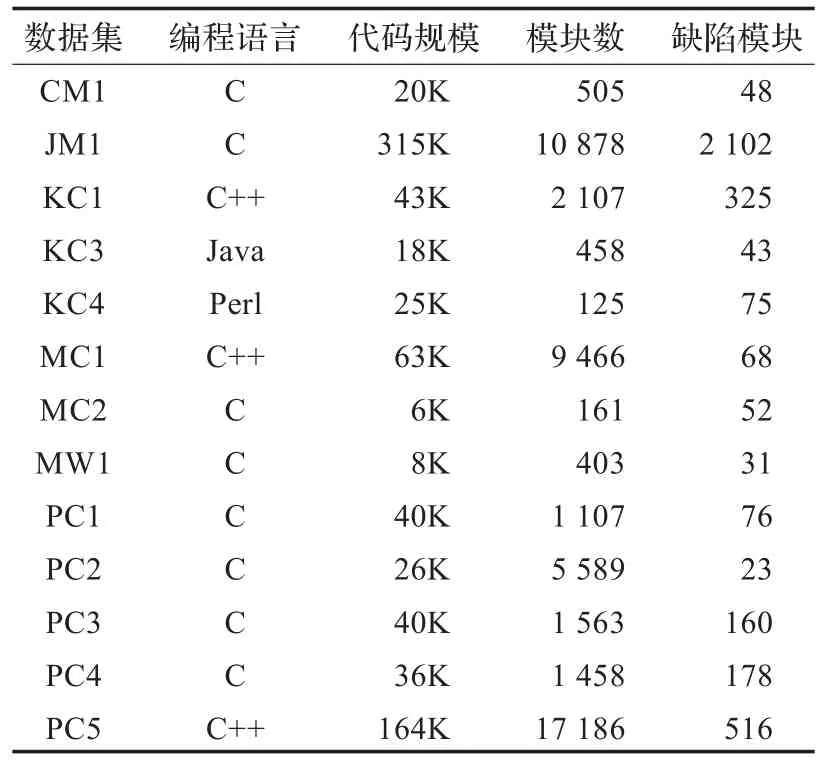
表1 实验数据

本文根据数据集属性Error_Count，对软件模块是否缺陷进行分类。设定Error_Count≥1的数据集认为是有缺陷的模块，否则为无缺陷的。并将数据集中每个属性值运用公式（5）进行标准化：

其中，x为属性值A的原始值，x′为属性A标准化后的值，minA是属性A的最小值，maxA是属性A的最大值。

4.2 实验评价标准

为了验证本文模型的预测能力，实验采用数据集[11]PC1、CM1、JM1、KC3，从数据集中分别随机抽取300、200、500、200个实验模块，采用十折交叉验证（10-fold CV）方法进行实验，即将数据集随机均分为10份，轮流将其中9份做训练，剩余的1份做预测，取10次实验度量值的平均值作为算法的运行结果。

为了与传统机器学习方法预测能力上作比较，本文采用准确度、查全率、查准率以及F1值来比较模型的预测能力。这些度量值首先要用到表2的交叉矩阵。

表2 二值分类交叉矩阵

评价标准指标定义如下：

准确度（accuracy）表示正确分类测试实例的个数占测试总实例个数的比例。计算公式如式（6）：

查准率（precision）表示正确分类的正例数占分类为正例的实例个数的比例。计算公式如式（7）：

查全率（recall）表示正确分类的正例个数占实际正例个数的比例。计算公式如式（8）：

F1表示查全率和查准率的调和平均。计算公式如式（9）：

其中，P为实际正例个数P=TP+FN,N为实际负例个数N=FP+TN,C为实验实例总数C=P+N。

4.3 实验结果与分析

图2（a）～（d）分别为本文所提出的算法与BP神经网络和决策树算法J48，在数据集JM1、CM1、KC3、PC1上运行10次的平均值，这里分别从准确度、查准率、查全率和F1值的角度给出对比。

从图2中可以看出：BP神经网络的预测总体较差，因为BP网络尚无一个有效的网络结构选择方法，网络结构和学习参数选择过分要求设计人员的经验，且泛化能力较差。基于决策树J48算法的预测模型的总体结果较好，但它受限于样本容量限制，需要对数据集进行多次的顺序扫描和排序，当训练集大得无法在内存容纳时程序无法运行。本文利用粒子群优化算法在全局的寻优能力，使之用于优化神经网络的权值和阈值，使得预测的各项指标优于BP神经网络和决策树J48算法，但每一粒子在给出位置及速度值，都要计算一次网络，故本文方法的计算成本需要进一步减少。

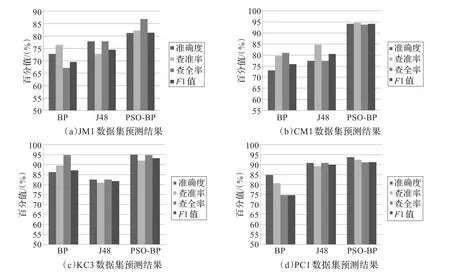
图2 PSO-BP方法与传统方法的比较

5 结论

本文的贡献是针对软件缺陷预测问题提出了一种新颖的基于PSO-BP的软件缺陷预测模模型。在数据集PC1、KC3、CM1、JM1上分别进行实验，并与J48和人工神经网络进行比较。实验结果表明，该模型比传统方法具有更好的预测效果，说明了模型的可行性。但是本文方法在优化权值和阈值过程中需要较长的时间，在今后的研究中将进一步降低模型的运行时间，提高模型的预测准确率。

[1]Challagulla V U B，Bastani F B，Yen I L，et al.Empirical assessment of machine learning based software defect prediction techniques[C]//Proceedings of the 10th IEEE International Workshop on Object-Oriented Real Time Dependable Systems，Washington，DC，USA，2005：263-270.

[2]陆民燕.软件可靠性工程[M].北京：国防工业出版社，2011.

[3]Feton N E，Martain N，William M，et al.Predicting software defects in varying development lifecycles using Bayesian nets[J]. Information and Software Technology，2007，49（1）：32-43.

[4]姜慧研，宗茂，刘相莹.基于ACO-SVM的软件缺陷预测模型的研究[J].计算机学报，2011，34（6）：1148-1154.

[5]冯少荣，尚文俊.基于样本选取的决策树改进算法[J].西南交通大学学报，2009，44（5）：643-647.

[6]Fast M，Assadi M，De S.Development and multi-utility of an ANN model for an industrial gas turbine[J].Applied Energy，2009，86（1）：9-17.

[7]Andreas W，Stefan W，Joachim W.Applying particle swarm optimization to software testing[C]//Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation，New York，NY，USA，2007：1121-1128.

[8]王青，伍书剑，李明树.软件缺陷预测技术[J].软件学报，2008，19（7）：1565-1580.

[9]Wu W，Wang J，Cheng M.Convergence analysis of online gradient method for BP neural networks[J].Neural Networks，2011，24（1）：91-98.

[10]Lu X，Li H，Yuan X.PSO-based intelligent integration of design an control for one kind of curing process[J].Journal of Process Control，2010，20（10）：1116-1125.

[11]Chapman M，Callis P，Jackson W.Metrics data program[EB/OL]. NASAIV and V Facility（2004）.http：//mdp.ivv.nasa.gov.

YU Anlei,PI Dechang

南京航空航天大学 计算机科学与技术学院，南京 210016

College of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

Software defect detection aims to automatically identify defective software modules that accelerates efficiently software test and improves the quality of a software system.Due to the application of traditional software prediction model being limited for its low accuracy and applicability,this paper puts forward a software prediction model based on PSO-BP,which employs Particle Swarm Optimization（PSO）to optimize weight and threshold value of BP.It uses cross-validation method as experiment method,and compares the results with other machine learning methods-BP and J48.The results show that PSO-BP has higher prediction accuracy.

software defect prediction;Artificial Neural Network（ANN）;Particle Swarm Optimization（PSO）

A

TP311

10.3778/j.issn.1002-8331.1208-0533

YU Anlei,PI Dechang.Software defect prediction model based on PSO-BP.Computer Engineering and Applications, 2013,49（7）：64-67.

江苏省高校“青蓝工程”；江苏省“333高层次人才培养工程”；航空科学基金（No.20111052010）。

于安雷（1988—），男，硕士研究生，主要从事数据挖掘的研究；皮德常（1971—），男，博士，教授，博导，主要从事数据挖掘与数据库的研究。E-mail：anleiyu@yahoo.cn

2012-09-07

2012-10-30

1002-8331（2013）07-0064-04

CNKI出版日期：2012-11-13 http://www.cnki.net/kcms/detail/11.2127.TP.20121113.1525.002.html