多车型开放式车辆路线问题的混合启发式算法

王晓博，任春玉，李海晨

多车型开放式车辆路线问题的混合启发式算法

王晓博，任春玉，李海晨

多车型开放式车辆路线问题，是物流配送优化中不可缺少的环节。针对标准遗传算法存在收敛速度慢，局部搜索能力差，易早熟的缺点，采用混合启发式算法进行优化求解。采用实数序列编码，使问题变得更简洁；有针对性地构建初始解，提高了解的可行性；用基于排序的选择与最佳保留相结合策略，保证群体的多样性；引入部分算术交叉算子，加强染色体的全局搜索能力；利用模拟退火算法的Boltzmann机制，控制遗传算法的交叉、变异操作，提高了算法的收敛速度和搜索效率。仿真结果表明混合启发式算法在求解质量和计算效率上好于标准遗传算法。

多车型开放式车辆路线问题；实数序列编码；部分算术交叉算子；Boltzmann机制；混合启发式算法

1 引言

开放式车辆路线问题（Open Vehicle Routing Problem，OVRP）是经典车辆路线问题（Vehicle Routing Problem，VRP）的拓展问题。OVRP和VRP最显著的区别在于：车辆在服务完最后一个顾客点后，不要求其回到出发车场，若需要回到车场，则必须沿原路返回。

目前研究较多的是车辆路线封闭问题，就是大家所熟知的VRP问题，但对于开放的车辆路线安排问题的研究结果还不多。

OVRP问题研究方法主要有精确算法、启发式算法和智能优化方法。精确性算法在可以求解的情况下，其解通常要优于人工智能算法；但其算法只能有效求解中小规模的OVRP问题[1]。

在解决实际较大规模的问题时，启发式算法能够在较少时间内，求出满足实际需要的满意解，尽管这个解实际上不是最优的。Bodin运用改进C-W节约算法来求解美国航空信件的邮递问题[2]。Sariklis给出了一种新的两阶段启发式算法：首先，考虑车载量的限制约束条件，先将顾客进行分组；其次，在每一组中确定最终的车辆路线；但其结果与最优结果有比较大的偏差[3]。Repoussis采用改进的贪婪算法求解开放式车辆路径问题[4]。Li提出基于扫描法和插入法的带记录效应启发式算法，求解带路程长度约束的OVRP问题[5]。

在求解大规模、复杂问题时，智能优化算法应用更广泛。Brandao通过最近邻居法和K度方法产生初始解，用禁忌搜索算法求解一类有能力约束的OVRP问题[6]。Fu通过随机的方法和最远者优先启发式算法FFH（Farthest First Heuristic）产生初始解，提出了解决有容量和路程长度约束的OVRP的禁忌搜索算法[7]。文献[8]利用禁忌搜索算法研究了无时间约束、有最大行驶时间约束和有时间窗约束的OVRP问题。钟石泉提出了核心路径的概念和原理，并设计有能力约束和距离约束的开放式车辆路径问题的禁忌算法[9]。Yslo改进了标准的模拟退火算法以一定的概率来接受较差的解，通过设定一个阈值T来决定是否接受一个解，并建立了基于阈值接收算法（Threshold Accepting，TA）的启发式算法[10]。Tarantilis在此基础上设立一个阈值的列表，算法迭代时每次则从阈值表中选择最大的元素作为阈值，算法迭代过程阈值列表不断更新[11]。李相勇提出了一种混合蚁群优化算法，其主体是一个在超立方框架下执行的MAX-MIN蚂蚁系统，计算结果表明该算法能有效地求解开放式车辆路径问题[12]。肖天国通过应用交叉、变异概率的自适应机制和交叉算子等技术，构造一个求解OVRP问题的遗传算法[13]。邓猛通过设计基于自然数编码的遗传算法来求解OVRP问题[14]。

然而，相对于OVRP，具有多车型的开放式车辆路径问题（Heterogeneous Open Vehicle Routing Problem，HOVRP）的研究相对较少，其建模与求解也更加复杂和困难。在实际的运营中，多用一辆车带来固定成本的增加远远比其因总里程缩短而减少的成本要大许多，因此减少服务的车辆数目是降低总成本的有效方法之一。

为此，本文以减少车辆数目为出发点，建立多车型的开放式车辆路径问题数学模型，并从整体上设计了求解HOVRP问题的混合启发式算法。

2 数学模型

式中，G{gr|r=1，2，…，R}为一系列可行R处的配送中心集合；H{hi|i=R+1，…，R+N}为一系列可行N处的客户集合；S{G}∪{H}为所有配送中心和客户总和；V{vlk|l= 1，2，…，L k=1，2，…，K}为L车型的运输车辆K集合；qi为客户需求量；为车辆类型的载重量；dij为客户i到客户 j的直线距离；为L车型的车辆K的最大行驶里程。

式（1）中，目标函数为求配送中心到客户运输里程的极小值；约束条件（2）确保每个客户仅由一个类型的一个运输车辆提供服务；约束条件（3）为运输工具容量的约束条件，满足在每条线路上行驶的车辆都不超过其载重量；约束条件（4）确保车辆最多只能到达某个客户点一次；约束条件（5）确保某一辆车最多只能从某收货点发出一次；约束条件（6）为运输车辆行驶里程都不超过其最大行驶里程。

3 混合启发式算法应用描述

3.1 实数序列编码

对于多车型配送问题，编码时考虑车辆的选取。因此，采用n位实数序列编码，其中配送货物的编号为n(1，2，…，n)，运输车辆的编号为k(1，2，…，k)。具体编码形式为(x1，x2，…，xi，…，xn)，每个基因的取值为 xi=k∈(1，2，…，k)。xi=k表示货物i安排在第k辆车上。以n=9，k=3编码(1，3，2，1，3，2，3，3，2)为例，编码表示一种配送方案为：货物(1，4)安排在1号车辆上；货物(3，6，9)安排在2号车辆上；货物(2，5，7，8)安排在3号车辆上。

3.2 初始解的形成

设hk为车辆k所运送的客户点总数，集合Rk={yik|0≤i≤hk}对应第k辆车运送的客户点，Yik表示车辆k服务于节点i，Y0k表示第k辆车的起始点为配送中心。初始解的形成步骤如下：

步骤2一条染色体上第i基因所对应的客户需求量为qi，令k=1。

步骤5如果k＞K，则k=K；否则，k=k。

步骤6k=k+1，转入步骤3。

步骤7i=i+1，转入步骤2。

步骤8重复步骤2至步骤7，K记录所用车辆总数，Rk记录一组可行路径。

3.3 适应度函数

采用轮盘赌选择法，要求适应度函数为非负，通过下面的变化将目标函数转化为适应度函数：

其中，fm为第m个染色体的适应度，n为一常数，z1为初始种群中最好染色体所对应的配送里程，zm为目前染色体所对应的配送里程。

3.4 选择算子

为了能够保持全局搜索能力，避免出现早熟现象，本文提出了一种将最佳个体保留与基于排序的选择策略相结合的最佳保留选择法。

表1 实验数据

设a、b是一个常数，满足关系b=2(a-1),1≤a≤2,文中取a=1.5,b=1。构造线性函数其中i=1，2，…，N。具体步骤如下：

步骤1计算种群中每个个体的适应度值 fi，并按非递增次序排序。

步骤2找出当前群体中适应度值最高的个体，令其为fbest。

步骤4随机生成一个[0，1]之间的数δ,如果 p1+…+ pi-1＜δ＜p1+…+pi-1+pi,选择个体i进入到下一代种群中，重复选择N次，生成下一代种群的N个个体。

步骤5找出新种群中适应度值最高的个体 f′now1和适应度值最低的个体 f′now2。

步骤6如果 f′now1＞fbest，则 fbest=f′now1；否则，用最好个体 fnow1替换目前群体中的最差个体 fnow2。

3.5 交叉算子

针对实数序列编码，采用部分算术交叉算子。部分算术交叉算子一方面保持了种群进化的多样性，保证算法能够收敛到全局最优；另一方面，能够保留双亲的优良基因组片断，限制不可行解出现，从而提高种群的收敛速度。

设两个父代个体分别为x0=(x1，x2，…，xn)，y0=(y1，y2，…，yn)，经交叉后得到的子个体为 x′=(x′1，x′2，…，x′n)和 y′= (y′1，y′2，…，y′n)。选择父代个体中第k位以后基因作为交叉段，在（0，1）之间随机生成n-k个随机数ak+1，ak+2，…，an，经交叉后得到的子个体定义为：

实验表明，对于实数编码，采用部分算术交叉算子比采用其他算子效率更高。

3.6 变异算子

对于变异操作，采用部分路径翻转的方式。经过验证，部分路径翻转的变异方式有利于跳出局部最优解，这种变异操作可以改善算法的效率。

3.7 模拟退火操作

设某代产生个体的适应度值为 f1，经过遗传算法的选择、交叉和变异，产生新个体的适应度值为 f2，设定Δf=f2-f1。

根据个体适应性的变异值Δf和概率值exp(-Δf/T)控制个体，具体步骤如下：

步骤1如果Δf＜0，适应度值 f2个体被保存在下一代里，并且适应度值 f1个体被从总体中删除。

步骤2如果Δf＞0，计算exp(-Δf/T)。

步骤3当exp(-Δf/T)＞[0，1]间的随机数，那么适应度值为 f1的个体保留在下一代中，适应度值为 f2的个体被删除。

步骤4当exp(-Δf/T)≤[0，1]间的随机数，那么适应度值为 f2的个体保留在下一代中，适应度值为 f1的个体被删除。

4 实验计算与结果分析

本实验数据取自文献[15]，并加以扩展。假设有18个顾客点，由中心派出车辆来完成各个顾客的需求。随机产生中心坐标（50，69）和18个顾客的坐标，各个顾客的需求量在（0，1）区间内随机产生，如表1所示。车辆分为A、B、C三种。A类载重量为1，数量若干；B类载重量为1.5，数量为3辆；C类载重量为1.8，数量为2辆。各客户之间与中心和客户之间距离均采用直线距离。

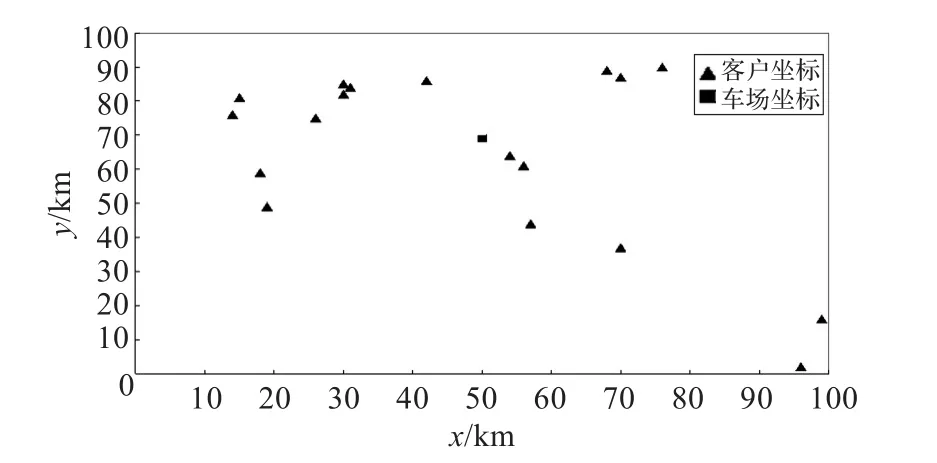
图1 中心和客户位置图

4.1 混合启发式算法求解

经反复实验，采用以下参数：群体规模取80，最大迭代次数取500，交叉概率 pc=0.83，变异概率 pm=0.016，初始温度T0=120℃，降温系数δ=0.75。随机求解10次，计算结果见表2。从表2中可以看出，在用本文设计的混合启发式算法对实例的10次求解中，都得到了质量较高的解，总里程的均值271.5 km，平均使用车辆5。算法的计算结果相当稳定，最差解的总里程仅比最好的解多4.6%。从计算效率上看，10次求解中有3次达到了最好解，2次达到了次最好解，可见效率较高。

表2 混合启发式算法求解HOVRP问题计算结果

其中，最好解的总里程266.6 km，具体行车路线见表3和图2。

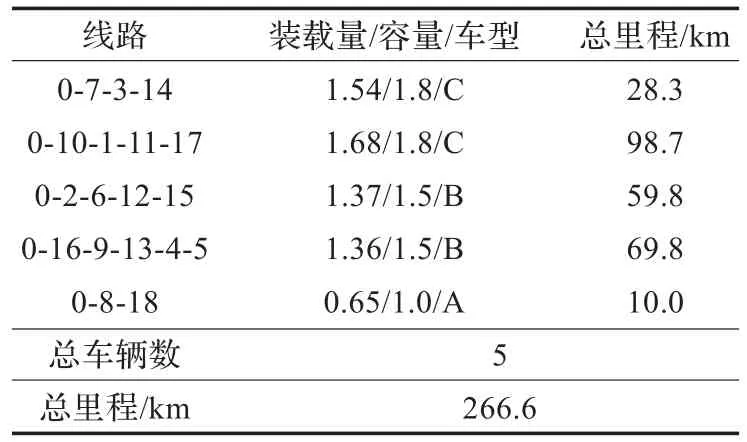
表3 优化结果

图2 配送路线图

4.2 混合遗传算法求解

[14-15]设计改进混合遗传算法，求解OVRP问题。为对比测试需要，本文采用此算法来求解HOVRP问题。

随机求解10次，计算结果见表4，其中，最优里程为229 km，具体见表5和图3。

4.3 两种算法比较

如表6，本文设计的混合启发式算法，无论在寻优结果、计算效率，以及算法的稳定性上均好于改进的遗传算法。

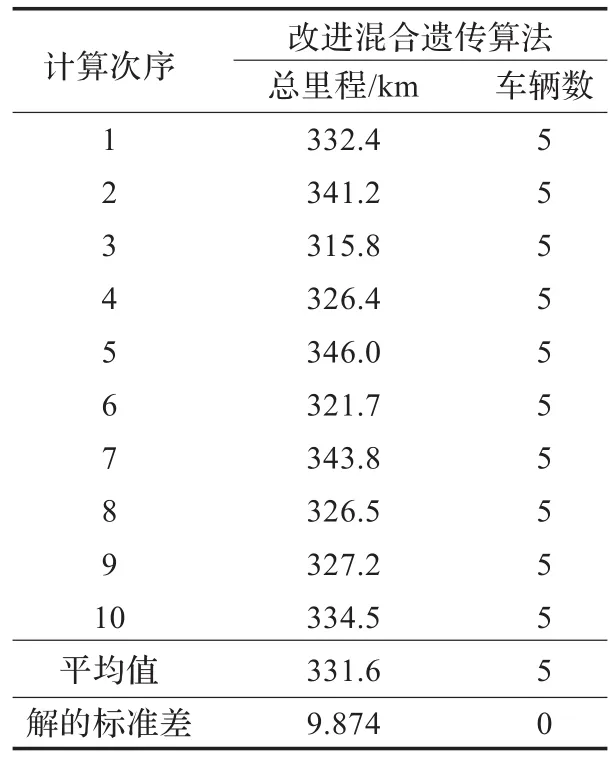
表4 改进混合遗传算法求解HOVRP问题计算结果

表5 车辆调度结果

图3 配送线路示意图

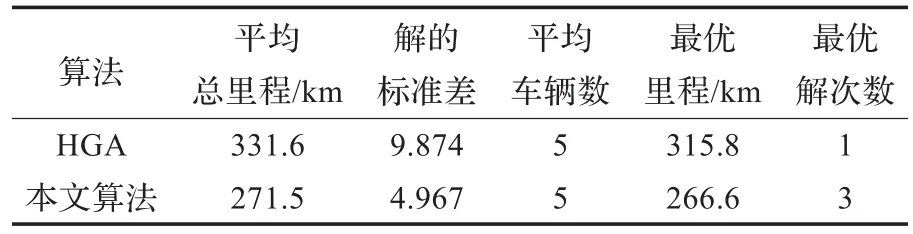
表6 改进混合遗传算法和本文算法比较

5 结论

仿真实验表明本文算法具有抗早熟能力强，收敛速度快和局部搜索能力强的特点，充分显示了其良好的寻优能力，大大提高了优化质量。本文算法为解决多车型开放式车辆调度问题提供了一个非常有效的求解方法。

参考文献：

[1]Letchford A N，Lysgaard J，Eglese R.A branch and cut algorithm for the capacitated open vehicle routing problem[J]. Journal of the Operational Research Society，2007，58（12）：1642-1651.

[2]Bodin L，Golden B，Assad A，et al.Routing and scheduling of vehicles and crews：the state of art[J].Computers and Operations Research，1983，10：63-211.

[3]Sariklis D，Powell S.A heuristic method for the open vehicle routing problem[J].Journal of the Operational Research Society，2000，51：564-573.

[4]Repoussis P P，Tarantilis D，Ioannou G.The open vehicle routing problem with time windows[J].Journal of the Operational Research Society，2007，58（3）：355-367.

[5]Li F，Golden B，Wasil E.The open vehicle routing problem：algorithms，large-scale test problems，and computational results[J]. Computers and Operations Research，2007，34：2918-2930.

[6]Brandao J.A tabu search algorithm for the open vehicle routing problem[J].European Journal of Operational Research，2004，157（3）：552-564.

[7]Fu Z，Eglese R，Li L.A new tabu search algorithm for the open vehicle routing problem[J].Journal of the Operational Research Society，2005，56（3）：267-274.

[8]Özyurt Z，Aksen D，Aras N.Open vehicle routing problem with driver nodes and time deadline[J].Journal of the Operational Research Society，2007，58：1223-1234.

[9]钟石泉，杜纲.基于核心路径禁忌算法的开放式车辆路径问题研究[J].计算机集成制造系统，2007，13（4）：827-832.

[10]Yslo M，Kowaklik J.Discrete optimization algorithms with pascal programs[M].Englewood Cliffs NJ：Prentice-Hall Inc，1983.

[11]Tarantilis C，Ioannou G，Kiranoudis C T，et al.Solving the open vehicle routing problem via a single parameter metaheuristic algorithm[J].The Journal of the Operational Research Society，2005，56：588-596.

[12]李相勇，田澎.开放式车辆路径问题的蚁群优化算法[J].系统工程理论与实践，2008（6）：81-93.

[13]肖天国，符卓.求解带软时间窗的开放式车辆路径问题的遗传算法[J].铁道科学与工程学报，2008，5（2）：79-83.

[14]邓猛，肖辉君，杨丰梅.开放的车辆路线安排问题的模型与遗传算法[J].北京化工大学学报，2006，33（4）：84-87.

[15]任春玉.开放式车辆路线问题的改进混合遗传算法[J].控制工程，2010，17（3）：356-359.

WANG Xiaobo,REN Chunyu,LI Haichen

黑龙江大学 信息管理学院，哈尔滨 150080

School of Information Management,Heilongjiang University,Harbin 150080,China

Heterogeneous open vehicle routing problem is logistics optimization indispensable part.According to the standard genetic algorithm shortcomings of slowly convergent speed,weakly partial searching ability and easily premature,hybrid heuristic algorithm is used to optimize the solution.The paper uses sequence of real numbers coding so as to simplify the problem,constructs the targeted initial solution to improve the feasibility,adopts a choice based on sort of a combination with the best retention strategies to ensure the diversity of population,and uses some arithmetic crossover operator to enhance whole search ability of the chromosome.Using Boltzmann simulated annealing mechanism for controlling genetic algorithm crossover and mutation operations,it improves the convergence speed and search efficiency.Finally,the good performance can be proved by experiment calculation and concrete examples.

heterogeneous open vehicle routing problem;sequence of real numbers coding;some arithmetic crossover operator;Boltzmann simulated annealing mechanism;hybrid heuristic algorithm

A

TP29

10.3778/j.issn.1002-8331.1108-0218

WANG Xiaobo,REN Chunyu,LI Haichen.Hybrid heuristic algorithm for heterogeneous open vehicle routing problem. Computer Engineering and Applications,2013,49（7）：243-247.

黑龙江省教育厅科学技术研究项目（No.11551332）。

王晓博（1973—），男，博士，副教授，硕士生导师，主要研究方向为物流系统仿真了；任春玉（1974—），女，副教授，主要研究方向为电子商务物流；李海晨（1971—），男，博士，副教授，主要研究方向为电子商务研究。E-mail：wangxb2010@163.com

2011-09-07

2011-11-10

1002-8331（2013）07-0243-05

CNKI出版日期：2011-12-09 http://www.cnki.net/kcms/detail/11.2127.TP.20111209.1001.037.html