求解强异类集装箱装载问题的混合蚁群算法
2013-08-07熊伟清
魏 平,熊伟清
求解强异类集装箱装载问题的混合蚁群算法
魏 平,熊伟清
针对强异类集装箱装载问题,设计了一种混合蚁群算法。算法中搜索空间分为货物摆放的优先序列和货物摆放的状态两部分;引入体积大的货物优先放入的启发式规则;将蚂蚁搜索得到的序列与历史最优序列进行交叉,取三者最优序列作为该蚂蚁的搜索路径;在更新信息素时,采取两种挥发系数更新信息素以避免信息素过快饱和,同时分析了算法的复杂度。通过三个强异类实例的测试,表明算法得到的装载方案有较高的空间利用率。
集装箱装载;蚁群优化算法;启发式规则;整数规划
1 引言
集装箱装载问题(CLP)是物流配送的重要环节,其方案的优劣对整个物流系统的效率以及运输成本有着重大的影响,有着广泛的应用背景,如在现实生活中的包装、裁剪、内存管理等。CLP是一个具有复杂约束条件的组合优化问题,在理论上属于NP-hard问题,通常实用的求解方法都是近似算法[1-2]。目前常用的求解方法有数学规划法、图论法、启发式方法、遗传算法、模拟退火算法,以及禁忌搜索算法等[3-4]。Bortfeldt[5]提出按照货物情形来进行分类:(1)“同类”问题,货物的规格完全相同,即单一尺寸货物的装填问题;(2)“强异类”问题,货物有很多不同的类型,每类货物数量很少;(3)“弱异类”问题,货物只有少数几种不同的类型,每类货物具有一定的数量。从分类可以看出,强异类集装箱装载是最复杂得一类集装箱装载问题。
蚁群优化算法(ACO)是一种仿生学算法,是由意大利学者M.Dorigo[6-7]等人提出的。目前蚁群算法在理论研究和实际应用上均取得了较大发展,已应用于众多优化领域,其中,在组合优化领域的应用最为广泛,包括旅行商问题(TSP)、二次指派问题(QAP)、车间作业调度问题(JSP)以及车辆调度问题(VRP)等。
考虑到蚁群算法在求解组合优化问题上的优势,本文尝试利用蚁群优化算法求解强异类集装箱装载问题。
2 集装箱装载问题数学模型
假设集装箱的长、宽、高分别为L、W、H,最大装载质量为G,货物的种类数为n,第i(i=1,2,…,n)类货物的长、宽、高、数量分别为li、wi、hi、ki。
装箱的目标为满足一定约束条件下最大化体积装载率或重量装载率,以提高集装箱的利用率,获得最佳的效益[1]:

λ为0-1变量。λ=1,表示以最大体积装载率为目标;λ=0,
CNKI出版日期:2011-12-09 http://www.cnki.net/kcms/detail/11.2127.TP.20111209.1000.017.html表示以最大重量装载率为目标。numi表示第i类货物装入集装箱的个数,其中0≤numi≤ki。
在实际的集装箱装载问题中,不同的情况需要考虑不同的约束条件。本文考虑如下限制条件:
(1)方向的约束。一般货物装载时的方向约束有两种,即任意旋转和水平旋转。
(2)货物稳定性的约束。货物装载应该使重心位于允许的范围内而确保整体稳定,以利于运输安全。假设货物的重心与货物的几何重心相同,则一件货物堆在另一件货物之上时,只要各边的尺寸的80%~100%被它下面的货物所支撑,那么这件货物在运输和装载过程中就不会倾倒,能够保持稳定。
(3)任意两件已放进集装箱的货物没有嵌入(即两货物重叠的体积不能大于0)。
(4)任一放进集装箱的货物的每一个面必须和集装箱的某一个面平行。
(5)任一放进集装箱的货物不能超出集装箱的边界。
3 空间三叉树定义与装载策略
3.1 空间三叉树定义
为了确保货物没有悬空现象,对空间采用三叉树分割法。当货物放入集装箱后,该集装箱被分割成前、右、上三个空间,每个子空间在装填货物过程中,在放入货物后同样被继续分割为三个空间[1]。空间划分如图1所示。

图1 空间划分示意图
空间三叉树定义如下:
空间三叉树
{
数据对象D:D表示可利用的空间
数据关系R:R是如下二元关系:
若D=Φ,则R=Φ,为空三叉树;
若D≠Φ,则R={H},H是如下二元关系:
在D中存在唯一的根元素root,若 D-{root}≠Φ,则存在D-{root}={Dt,Dr,Df},且Dt∩Dr=Φ,Dt∩Df=Φ,Dr∩Df=Φ。
若 Dt≠Φ,则 Dt中存在唯一的元素 xt,<root,xt>∈H,且存在 Dt上的关系Ht⊂H;若Dr≠Φ,则Dr中存在唯一的元素xr,<root,xr>∈H,且存在Dr上的关系Hr⊂H;若Df≠Φ,则Df中存在唯一的元素 xf,<root,xf>∈H,且存在Df上的关系Hf⊂H。H={<root,xt>,<root,xr>,<root,xf>,Ht,Hr,Hf};
(Dt,{Ht})是一棵符合本定义的三叉树,为根的左子树,(Dr,{Hr})是一棵符合本定义的三叉树,为根的中子树,(Df,{Hf})是一棵符合本定义的三叉树,为根的左子树。
基本操作P:
CreateChild(T,e):T为当前生成的三叉树,e为T的叶子结点,设GS表示未装入集装箱的货物集,V表示结点e代表的空间,GV表示能装入V的货物集(GV={g|g∈GS,V≥g}),若GV≠Φ,选择其中一件货物装入V,并为结点e产生三个子结点;否则结点e为最终生成三叉树的叶子结点。
CreateTree():根结点代表集装箱的空间,通过操作CreateChild(T,e),按照左子树、中子树和右子树的顺序深度优先构造三叉树,最终生成的三叉树对应一个装载方案。
}
其中,<root,xt>,<root,xr>,<root,xf>表示在空间root中装入货物后,xt、xr、xf分别为将空间root划分产生的上空间、右空间、前空间。
3.2 装载策略
一次装箱过程实际可以看做一棵三叉树的建立过程,结点代表可利用的空间,一个结点是否还有子结点取决于是否还有货物能装入该结点所代表的空间。由于可利用空间可用三叉树来表示,那么可用递归算法进行描述:
步骤1把一件货物装入一个可利用空间中,将可利用空间分成三个子空间。
步骤2把每个子空间中按照步骤1的方法递归的装入货物。如果子空间的大小只能装入一件货物,那么,就把那件货物直接装入子空间中。
步骤3每个子空间的解结合起来就是装箱问题的解。伪代码如下:

4 混合蚁群算法设计
4.1 目标函数
对于集装箱装载问题,关注的目标可能有多方面,例如容积利用率、重量装载率、稳定性等,但容积利用率是集装箱装载问题最为关注的目标。本文以集装箱的容积利用率最大化为目标,即取λ=1,目标函数为:

各参数含义见第2章。
4.2 编码和解码
(1)编码
对于每个可利用的空间,要选择一件货物以某一状态装入。因此,编码时考虑货物装载优先顺序和货物放置状态。编码 p={p1,p2,…,pn},对于 pi(i=1,2,…,n)包含两部分,货物的编号ki(1≤ki≤n)和放置状态si,其中∀i≠j,ki≠kj。
货物状态定义如下:
对于第i类货物,若方向上没有约束,则其放置的状态有P33=6种(固定集装箱的L、W、H顺序,货物l、w、h的全排列)。分别为

若方向上有约束(某个面必须朝上),则其放置的状态有P22=2种。分别为:

(2)解码
根据编码p得到实际装载方案步骤如下:
步骤1栈S保存可利用的空间,初始时保存集装箱的空间。
步骤2若S中还有可利用的空间,取出栈顶的空间作为当前待装空间V;否则结束。
步骤3按照编码p中的顺序,依次对 pi进行判断,直到满足如下条件:货物ki未装入,并且按状态si能装入V中。
步骤3.1若存在这样的货物,则按指定状态放入集装箱,将货物ki标记为已装入,将V划分成三个子空间压入S,返回步骤2。
步骤3.2若不存在这样的货物,则丢弃空间V,返回步骤2。
4.3 算子设计
(1)序列选择
蚂蚁根据路径上的信息素以及启发信息选择货物序列。t时刻,蚂蚁k选择首件货物编号为i的概率(t)为:

蚂蚁k选择货物i后紧接着选择货物j的概率 pkij(t):

其中,τi,j(t)为t时刻从货物i到货物j的信息素,为t时刻蚂蚁k在选择货物i后剩余未被选择货物的集合。初始时货物序列信息素如下:

选择货物后,为该货物选择摆放状态。对于货物i选择状态s的概率为:

(2)交叉操作
将蚂蚁搜索得到的序列与历史最优序列进行交叉,取三者最优序列作为该蚂蚁的搜索路径。为了保证交叉后还是有效序列,即同一个货物编号不能在序列中重复出现,将蚂蚁搜索得到的序列 p1与历史最优序列 p*进行序交叉,得到两个新的序列 p2,p3。将序列 p1,p2,p3解码,取其最优序列作为该蚂蚁的搜索路径。设历史最优序列为:,当前蚂蚁搜索的序列为:p1={p11,p12,…,p1n}。
序交叉具体操作如下:
步骤1随机取交叉位a(1≤a≤n-2),p2={p11, p12,…,。
2一元素的货物编号相同,若存在相同,测试下一元素;否则,将该元素加入到序列p2中。
(3)信息素更新
若本代最优值大于历史最优值时,则更新货物序列信息素和货物状态信息素。避免某些路径的信息素过快饱和,本文依据上次更新情况采用不同的挥发系数,将本代最优路径与上一次更新的路径进行比较,对于那些相同的子路径,用较小的挥发系数进行更新。设上次更新时,首件货物编号为f,货物i的摆放状态为 psi,后继货物编号pni。本代最优序列为 p={p1,p2,…,pn},对于结点 pi的货物编号为ki,状态为si。首件货物信息素更新:

其中,ρ1、ρ2为两种挥发系数,ρ2>ρ1。
后继货物信息素更新:


货物状态信息素更新:

其中,ρ′1、ρ′2为两种挥发系数,ρ′2>ρ′1。
4.4 算法步骤
求解强异类集装箱装载问题算法步骤如下:
步骤1初始化货物序列信息素和货物状态信息素、迭代次数loop、蚂蚁个数m,挥发系数ρ1,ρ2,ρ′1,ρ′2。
步骤2 m只蚂蚁按公式(3)、(4)、(6)分别进行遍历,得到序列,并与历史最优序列进行交叉、解码,取最优序列作为该蚂蚁遍历的序列。
步骤3若本代最优解Pcurrent优于历史最优解Pbest,按照公式(7)、(9)、(11)更新序列信息素和状态信息素。若当前代数q<loop,返回步骤2;否则结束。
4.5 算法时间复杂度分析
设货物数量为n,蚂蚁个数为m,迭代次数为loop,每只蚂蚁搜索货物装入优先序列的时间复杂度为O(n2),搜索货物状态序列的时间复杂度为O(n),对得到的序列进行交叉的时间复杂度为O(n2),对序列进行解码的时间复杂度为O(n2),信息素更新的时间复杂度为O(n2),故算法总的时间复杂度为O(loop×m×n2)。
5 实验结果
参数设置如下:ρ1=0.08,ρ2=0.15,ρ′1=0.05,ρ′2=0.1,m=50,loop=500。
算例1实验数据来源于文献[8]。具体数据如下:待装集装箱为一个6 096 mm国际标准的集装箱,尺寸为2 352 mm× 2 388 mm×5 899 mm。货物尺寸见表1。

表1 算例1货物数据
图2和图3所示为本文算法求解算例1的装载方案,体积利用率为89.04%,而文献[8]得到的体积利用率为85.19%。

图2 算例1装载计划表

图3 算例1装箱效果图
算例2实验数据来源于文献[9]。具体数据如下:待装集装箱为一个6 096 mm国际标准的集装箱,尺寸为235.2 cm× 238.8 cm×589.9 cm。货物尺寸见表2。

表2 算例2货物数据
图4和图5所示为本文算法求解算例2的装载方案,体积利用率为85.83%,文献[9]得到80%的利用率,文献[10]得到82.8%的利用率,文献[11]得到85.04%的利用率。

图4 算例2装载计划表
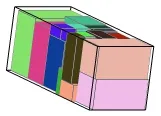
图5 算例2装箱效果图
算例3实验数据来源于文献[12]。具体数据如下:待装集装箱尺寸为5.8 m×2.4 m×2.4 m。货物尺寸见表3。

表3 算例3货物数据
图6和图7所示本算法求解算例3的装载方案,体积利用率为87.16%。文献[12]得到总空间利率为83.3%,文献[13]得到总空间利率为82.7%。

图6 算例3装载计划表

图7 算例3装箱效果图
6 结束语
集装箱装载问题的搜索空间分为货物摆放的优先序列和货物摆放的状态两部分,对应设计了两种信息素序列信息素和状态信息素,在更新信息素时,采取两种挥发系数更新信息素以避免信息素过快饱和。另外,引入体积大的货物优先放入的启发式规则,将蚂蚁搜索得到的序列与历史最优序列进行交叉,取三者最优序列作为该蚂蚁的搜索路径。通过三个实例计算结果表明,本文设计的混合蚁群该算法可以得到一个合理的布局及装载方案,提高集装箱的空间利用率;同时,也表明在具体应用中,蚁群算法结合启发式规则求解像集装箱装载等组合优化问题是有效的设计方案;说明将智能优化算法和具体问题的启发式算法结合有利于问题的求解。
[1]Bischof E E.Three-dimensional packing of items with limited load bearing strength[J].European JournalofOperationalResearch,2006,168(3):952-966.
[2]Wu Y,Li W,Goh M,et al.Three-dimensional bin packing problem with variable bin height[J].European Journalof Operational Research,2010,202(2):347-355.
[3]屈援,王雪莲.基于禁忌算法的多约束集装箱装载问题研究[J].中国航海,2007,73(4):73-76.
[4]许光泞,俞金寿.应用自适应遗传算法解决集装箱装载问题[J].控制与决策,2007,22(11):1280-1283.
[5]Bortfeldt A.A genetic algorithm for the container loading problem[C]//Proceedings of the Conference on Adaptive Computing and Information Processing,London,1994,44:145-159.
[6]Dorigo M,Stützle T.Ant colony optimization[M].[S.l.]:MIT Press,2004.
[7]Dorigo M,Caro G D.Ant colony optimization:a new metaheuristic[C]//Proc ofthe 1999 Congress on Evolutionary Computation.Washington,DC,USA:IEEE Press,1999:1470-1477.
[8]许光泞,俞金寿.集装箱装载问题的一种DNA遗传算法计算机[J].计算机工程与应用,2008,44(22):237-240.
[9]Gehring H,Menschner K,Meyer M.A computer-based heuristic for packing pooled shipment containers[J].European Journal of Operational Research,1990,44:277-288.
[10]姜义东,查建中,何大勇.集装箱装载矩形货物的布局研究[J].铁道学报,2002,22(6):13-18.
[11]刘嘉敏,马广煜,黄有群.基于组合的三维集装箱装入启发式算法的研究[J].工程图学学报,2005(1):22-25.
[12]王若恩,陈锦昌,郭水平.三维空间最优装载模式的算法研究与实现[J].工程图学学报,2005(5):6-13.
[13]王亚英,邵惠鹤,田雅杰.一种平板车装载问题的启发式算法[J].计算机工程,2001,27(4):87-88.
WEI Ping,XIONG Weiqing
宁波大学 电子商务与物流研究所,浙江 宁波 315211
Institute of Electronic Commerce and Logistics,Ningbo University,Ningbo,Zhejiang 315211,China
Aiming at the strongly heterogeneous Container Loading Problem(CLP),a mixed Ant Colony Algorithm(ACO)is designed.The solution of problem is divided in two parts,the priority of the goods and the goods'state.Based on heuristic rules,the larger goods have priority to pack in container,so volume is considered as heuristic information.The sequence that ant has searched crosses with historical optimal sequence.The optimal one among the three sequences is choose as the wanted sequence.In order to avoid pheromone over-rapid saturated,pheromone is updated by adopting two volatile coefficients.The complexity of the algorithm is analyzed.Through testing three examples,the space utilization is high by using this algorithm.
Container Loading Problem(CLP);Ant Colony Algorithm(ACO);heuristic rules;integer programming
A
TP391
10.3778/j.issn.1002-8331.1108-0361
浙江省自然科学基金(No.Y1100052);浙江省教育厅科研项目(No.Y201017000)。
魏平(1965—),女,副教授,主要研究方向:进化计算,计算智能等;熊伟清(1966—),男,教授,主要研究方向:进化计算,计算智能,软件工程等。E-mail:weiping@nbu.edu.cn
2011-08-25
2011-10-13
1002-8331(2013)07-0252-06
WEI ping,XIONG Weiqing.Hybrid binary ant colony algorithm for strongly heterogeneous container loading problem. Computer Engineering and Applications,2013,49(7):252-257.
