圆环腔内纳米流体自然对流的数值研究

王文龙，徐 旭，王宇飞，范利武，俞自涛

（1.中国计量学院 计量测试工程学院，浙江 杭州 310018；2.浙江大学 能源工程学系，浙江 杭州 310027）

自然对流传热是一个重要的自然现象，由于其广泛的应用在电子工程系统冷却、热交换和制冷系统，从工业和节能的方面考虑，增强这项系统中的热能量转移是非常必要的.传统的纯液体换热工质导热系数低，很难满足一些换热交换系统特殊结构的限制和高负荷传热强度的传热和冷却要求［1］.因此，进一步研制高导热率、传热性能好的换热工质显得非常必要.1995年，美国 Argonne国家实验室的Choi［2］等人提出纳米流体的概念.纳米流体是指以一定方式和比例，在液体介质中添加纳米金属或非金属粉末，制备成均匀、稳定的新型传热工质.这种方法在过去十年得到广泛的研究.2003年，Khanafer［3］首次采用数值模拟研究了二维矩形容器内Cu－水纳米流体传热特性.结果显示：在不同格拉晓夫数下，纳米流体的自然对流换热性能随着Cu纳米颗粒体积分数的增加而显著增强.Putra［4］等通过实验研究了水平圆环内Al2O3－水和CuO－水纳米流体的自然对流传热特性.结果显示：纳米流体的传热特性比水的要差，并且随着纳米颗粒体积分数的增加传热特性恶化的越明显.Wen等［5，6］研究了水平管内直径为30～40nm纳米TiO2－水纳米流体的自然对流传热特性.结果发现，纳米流体的自然对流换热系数比单纯的水低，并且随着纳米浓度的增加而不断减小.Nada等［7］研究了纳米流体导热系数和黏度对水平圆环内自然对流影响.实验研究和数值研究的差异，可能由于数值研究采用的是单相模型，并没有考虑颗粒间的相互作用，也忽视了颗粒形状和大小的影响.而实验研究中颗粒的沉淀和团聚也会对结果有一定的影响.由于纳米流体在传热中具有巨大的应用前景，因此，对纳米流体的研究非常必要.

目前国内外对于纳米流体自然对流的研究工作，数值模拟的研究占较大的比重.数值模拟是通过数学建模研究工程基础问题的有效手段，也是拓展和弥补高成本的实验研究的有效途径.本文通过对圆环封闭腔内的Ag－水纳米流体自然对流传热进行数值模拟，将Ag－水纳米流体视为单相的流体来研究，将热物参数带入计算，分析封闭腔内的传热特性，计算得到瑞利数、纳米粒子添加量和圆环半径比对封闭腔内自然对流传热性能的影响，并对可能的原因进行了分析.

1 物理模型和控制方程

计算模型为二维水平圆环封闭腔，在两个圆之间的圆环中充满纳米流体.内外圆环壁均为恒温，内圆环壁为高温Ti，外壁为低温To.其物理模型如图1所示.

图1 圆环物理模型Figure 1 Sketch of problem geometry

假定纳米流体为连续介质，即采用单相模型.其控制方程如下：

式中u和v分别为径向速度和角速度，υ、ρ、g和a分别为运动黏度、密度、重力加速度和热扩散系数.纳米流体的热物理参数见表1.

表1 水和纳米粒子的热物理性质Table 1 Thermal physical properties of water and Ag

纳米流体的热物性参数包括流体密度、黏度、导热系数和定压比热.流体的热物性均采用参考温度下（To＋Ti）／2即内外壁平均温度下的值.纳米流体的密度和比热通过两相混合物拟合计算得到，表达式如下：

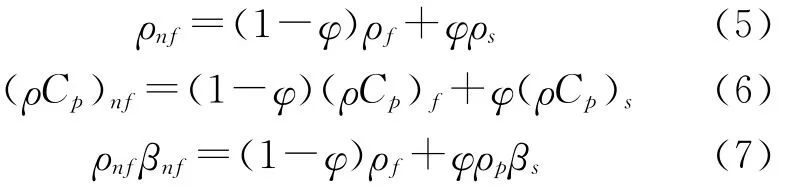
式中：ρnf、ρf和ρs分别为纳米流体与基液和纳米颗粒的密度，Cp和β分别为定压比热和热膨胀系数，φ为颗粒体积分数.

纳米流体的黏度计算采用Brinkman［8］黏度计算模型：

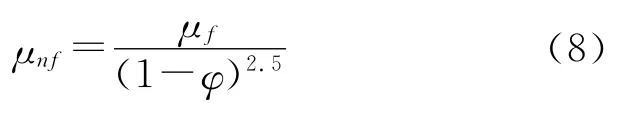
式中unf和uf分别为流体和基液的黏度.

流体的导热系数可以通过数值模拟［9］和理论模型公式得出，本文采用Maxwell［10］经典模型：

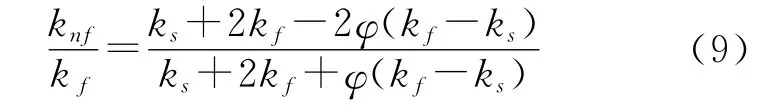
瑞利数（Ra）定义如下：

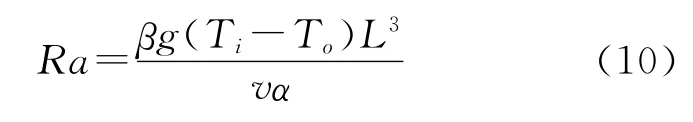
其中knf、kf和ks分别为纳米流体与基液和纳米粒子的导热系数.L为特征长度，L＝Ro－Ri，对应不同的特征长度，瑞利数变化范围在103到106之间，使自然对流控制在层流状态.本文采用Ag纳米粒子，内圆壁温度为303K，外圆壁温度为283K.采用Fluent软件对上述模型进行模拟求解，运用Boussinesq假设.压力和速度耦合采用SIMPLE算法，压力修正采用PRESTO算法，动量方程和能量方程采用二阶迎风格式.计算区域采用四边形网格划分，并对壁面网格进行加密处理.通过参照文献［7］中的网格尺寸，得到本模型中的网格数为1万.连续方程精度为10－4，其他精度为10－7，迭代502次收敛.

2 结果与分析

2.1 纳米颗粒浓度的影响

图2是水和体积分数为5%的Ag－水纳米流体在不同Ra数下的温度等值线.从图中可以看出，当Ra＝103时，φ＝0%和φ＝5%的温度等值线非常规则均匀，与圆环壁面相一致，此时内外壁间对流比较微弱，内外壁间的换热主要以热传导为主.随着Ra数的增加，圆环顶部θ＝180°处温度等值线不断向两侧扩散，越来越尖锐.Ra＝106时内外壁间的温度等值线已变为水平状，内外壁间的传热强度不断加剧，圆环内的传热逐渐由热传导向对流转变.同时，在Ra＝104和105时，在θ＝180°区域同一Ra数下，水的温度等值线比5%体积分数的纳米流体的等温线尖锐、突出.这说明圆环内水的流动较纳米流体更为剧烈，换热强度也更大.这是由于添加纳米粒子增加了流体导热系数，强化了圆环内的传热，但是黏度的增大使得对流恶化，而且，黏度对传热的恶化要大于导热系数对传热的强化.因此，在基液中添加Ag纳米颗粒减弱了换热效果.

图2 水和5%体积分数纳米流体的温度等值线Figure 2 Temperature isotherms of water and 5%particle volume fraction

努赛尔数是判别自然对流换热强弱的重要依据，壁面局部努赛尔数Nu和平均努赛尔数＜Nu＞分别定义如下：

式中q为热流密度，knf为纳米流体的导热系数，L为特征长度.

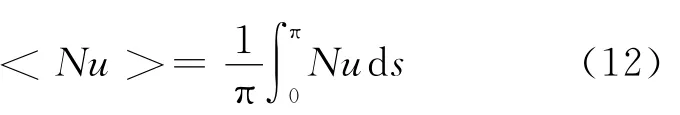
图3为水和纳米流体在不同Ra数下内圆环壁面θ从0°到180°区域局部Nu数分布.从图可以发现，在Ra＝104和Ra＝106时，内壁表面Nu数变化趋势一致，在整个壁面区域纳米流体的Nu数均小于水，且随着颗粒体积分数的增大Nu数不断减小.同时，不同体积分数间Nu的差异随着θ的增大而减小，即在圆环底部自然对流最为剧烈，且随着θ的增大对流逐渐减弱，不同颗粒体积分数流体间的换热差异不断减小.在Ra＝103时，Nu在θ＜120°时随着颗粒浓度的增大而减小，但在θ＞120°之后却随着颗粒的增加而增大.这是由于Ra＝103时，圆环内传热以热传导为主，且随着流体导热系数增加而增强.因此，在θ＞120°时随着体积分数的增加传热不断增强.并且，颗粒浓度越大，壁面上Nu值变化的越小.例如，体积分数为φ＝1%和φ＝9%在θ＝0°到θ＝180°处Nu减小量分别为0.73和0.57.Ra＝105时，壁面Nu数分布与Ra＝104和Ra＝106基本一致，但在φ＝1%时的Nu数比水的大.这说明在Ra＝105时，添加量在1%体积分数纳米颗粒能够强化传热.

图3 内壁面局部努塞尔数分布Figure 3 Nusselt number distribution around inner cylinder surface

内壁面平均努塞尔数分布如图4.添加纳米颗粒的流体平均努塞尔数均小于水，且随着颗粒体积分数的增加不断下降，在基液中添加纳米颗粒降低了其换热效果.在基液中添加纳米颗粒虽然能提高纳米流体的导热系数，增强传热；但是流体的黏度的增加导致纳米流体的流动强度下降，换热作用减弱.并且，黏度对传热的恶化要大于导热系数对传热的强化.

由圆环尺寸导致瑞利数的改变对自然对流影响非常显著，探究瑞利数对腔体自然对流换热作用非常有必要.基液在不同瑞利数下的平均努塞尔数及其拟合曲线如图5.从图中可以发现，瑞利数在103到106范围内，平均努塞尔数随着瑞利数的增加而增大，尤其是在高瑞利数下增大的非常显著.

同时，对图中数据进行拟合，得到平均努塞尔数与Ra的关联式：

此关联式的平均相对误差为2.1%，最大相对误差为5.3%.

2.2 圆环半径比的影响

不同的流动形态对自然对流传热影响很大，通过改变半径比（Ri／L）观察其对传热的作用.图6给出了流体在Ra＝104时不同半径比的温度等值线图.如图所示，在Ri／L＝0.5时，温度等值线在θ＝180°处由内壁向外壁扩散、突出，温度等值

线扰动很大，圆环间的流动非常剧烈.随着Ri／L的增大，温度等值线逐渐变得均匀，扰动越来越微弱.特别是在Ri／L＝3处，温度等值线与圆环壁面一致.可见，Ri／L 对自然对流影响剧烈，Ri／L越小，自然对流换热强度越大，这与Yu［11］的研究相一致.这可能是由于Ri／L越小，内外圆环周长比越小，圆环内的流动强度越大，换热越显著.

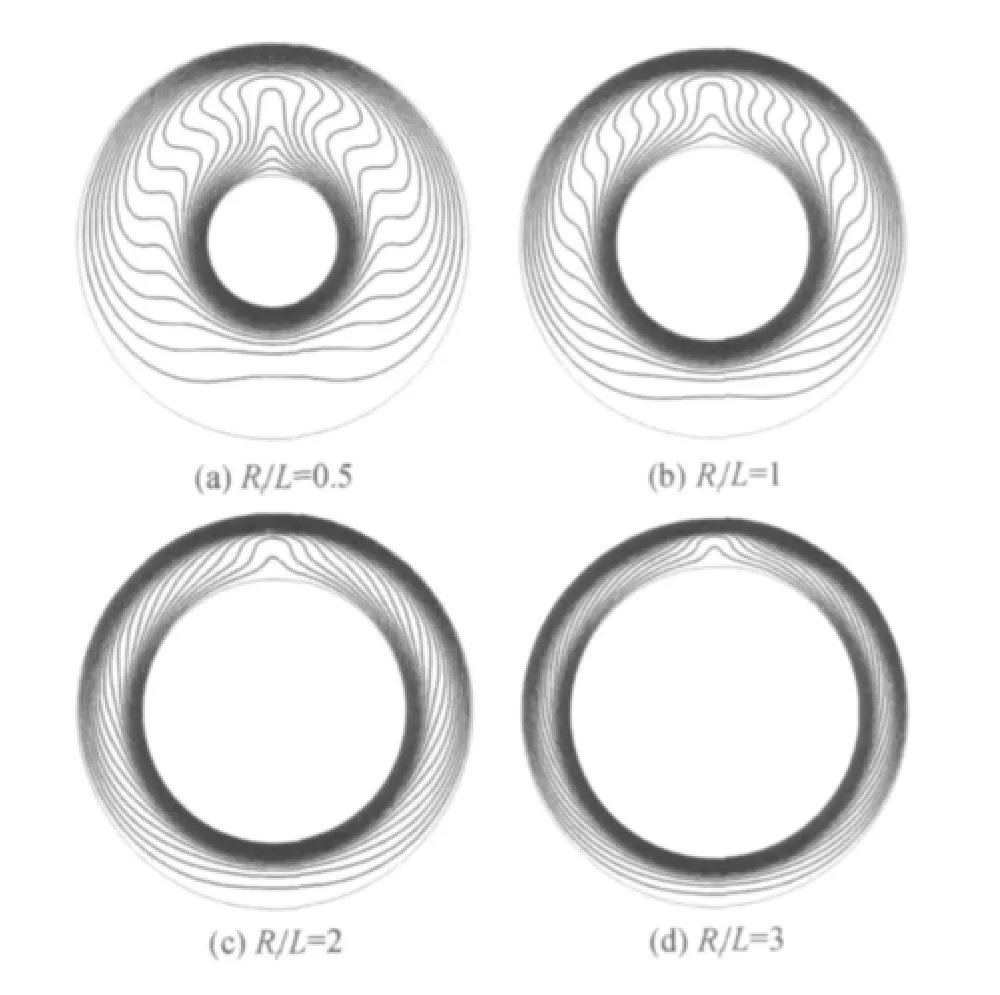
图6 Ra＝104时不同半径比的温度等值线Figure 6 Temperature isotherms of Ra＝104 with dif ferent radius ratio

为了更加详细的研究半径比对圆环自然对流的影响，给出了水在Ra从103到106变化范围下不同Ri／L时的平均努塞尔数分布如图7.显然，在任一Ra数下，平均努塞尔数均随着Ri／L的增大而不断减小，特别是在高Ra数时下降的非常显著.当Ra＝106时，相邻Ri／L间＜Nu＞的下降量分别为2.63、2.04和0.85，Ra＝103时的下降量分别为0.48、0.26和0.09.可见，Ra 数越大，平均努塞尔数在同一半径比变化下改变的越大，并且随着Ri／L的增大，＜Nu＞的下降趋势不断减缓，特别是当Ri／L＞2时＜Nu＞的变化非常微弱.同时还发现，Ra＝105、Ri／L＝0.5处的＜Nu＞值比Ra＝106、Ri／L＝3处的要大，与Ra＝106、Ri／L＝2时的相接近.可见，Ri／L 对圆环自然对流作用非常显著.

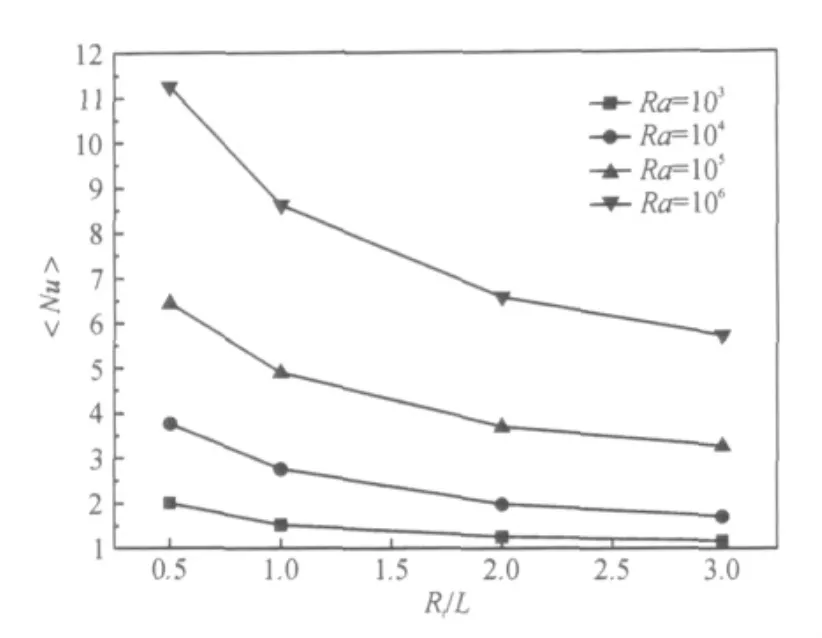
图7 水在不同Ri／L下的＜Nu＞数Figure 7 Average Nusselt of water with different radius ratio

3 结 语

采用数值方法研究了圆环内Ag－水纳米流体自然对流换热特性，探究了瑞利数、纳米粒子添加量和圆环半径比传热性能的影响.计算结果表明，自然对流传热性能随着瑞利数的增加而增强，随着纳米粒子浓度和圆环半径比的增加而减弱，特别是在高瑞利数下变化非常显著.同时，当瑞利数较小时，圆环壁间的传热主要由热传导为主，随着瑞利数的不断增大，换热逐渐由热传导向对流转变，传热不断增强.因此，通过增大瑞利数和减小半径比可以有效强化圆环传热.

［1］宣益民，李 强.纳米流体能量传递理论与应用［M］.北京：科学出版社，2009：1－2.

［2］Choi S U S，Eastman J A.Enhancing thermal conductivity of fluids with nan－oparticles［C］／／Developments and Applications of Non－Newtonian Flows.New York：ASME，1995：99－105.

［3］Khalil K，Kambiz V，Marilyn L.Buoyancy－driven heat transfer enhancement in a two－dimensional enclosure utilizing nanofluids［J］.International Journal of Heat and Mass Transfer，2003，46（19）：3639－3653.

［4］Nandy P，Wilfried R，Das S K.Natural convection of nanofluids［J］.Heat and Mass Transfer，2003，39（8，9）：775－784.

［5］Wen D S，Ding Y L.Formulation of nanofluids for natural convective heat transfer applications［J］.International Journal of Heat and Fluid Flow，2005，26：855－864.

［6］Wen D S，Ding Y L.Natural convective heat transfer of suspensions of titanium dioxide nanoparticles（nanofluids）［J］.IEEE Transactions on Nanotechnology，2006，5（3）：220－227.

［7］Eiyad A N.Effects of variable viscosity and thermal conductivity of Al2O3－water nanofluid on heat transfer enhancement in natural convection［J］.International Journal of Heat and Fluid Flow，2009，30：679－690.

［8］Brinkman H C.The viscosity of concentrated suspensions and solutions［J］.Journal of Chemical Physics，1952，20：571－581.

［9］潘 江，王玉刚.瞬态热线法导热系数测量的数值模拟［J］.中国计量学院学报，2008，19（2）：108－113.Pan Jiang，Wang Yugang.Numerical simulation of measurement of thermal conductivity with transient hot wire method［J］.Journal of China Jiliang University，2008，19（2）：108－113.

［10］Maxwell J C.A Treatise on Electricity and Magnetism［M］.2nd ed.Cambridge：Oxford University Press，1904：435－441.

［11］Yu Z T，Xu X，Hu Y C，et al.A numerical investigation of transient natural convection heat transfer of aqueous nanofluids in a horizontal concentric annulus［J］.International Journal of Heat and Mass Transfer，2012，55（4）：1141－1148.