10kN载荷下钢丝绳拉伸模拟及其声发射特征分析

聂 林，钱晓耀，袁昌明，张维刚

（中国计量学院 质量与安全工程学院，浙江 杭州 310018）

钢丝绳因其具有弯曲性能好、弹性好、高速运行无噪声、重量轻、结构多样等特点，被作为承载和（或）牵引构件广泛应用于桥梁、索道、吊桥、煤炭、冶金、石油、高层建筑等领域.钢丝绳最主要的失效方式是疲劳，钢丝绳内部接触部分受力具有复杂性，其安全性能关系到生命和财产的安全，使用声发射技术可以对加载状态下的钢丝绳进行全过程的检测［1-2］.

声发射（acoustic emission）无损检测技术是一种动态的检测方法，由于声发射技术可以探测到来自被测构件自身应力、应变能在构件变形中产生的能量，且可以通过实时在线检测追踪缺陷的活动规律，正是因为这些优点，声发射技术在生产现场和应用现场的实时无损检测中得到广泛的应用［3］.

最早在钢丝绳缺陷检测中使用声发射技术的英国的J.L.Taylor和N.F.Casey，他们通过大量试验证明了该方法用于检测钢丝绳断丝过程的有效性.国内东北大学邵永波等1998年首先将声身发射技术用于检测钢丝绳的缺陷当中，研究了钢丝绳失效、疲劳损伤、去噪以及断丝的模式识别.中国科学院朱祖铭等研究了钢丝绳的疲劳损伤和其声发射行为机制的关系，通过大量试验证明了声发射检测钢丝绳缺陷的适用性［4-7］.声发射能量是材料受载荷后内部变化引起的局部应变，该局部应变能作为快速释放产生的瞬时弹性波能量的度量，它是声发射各种参数的综合体现.金属材料的声发射反映了其损伤的程度，与材料内部的缺陷的演化相关.哈尔滨工业大学李冬生等通过对钢绞线拉伸试验全过程的监测，指出钢绞线整个损伤过程的声发射特征的声发射的累计能量与拉伸过程中应力随应变的变化具有一致性，其拟合结果很理想，相关系数达到0.994，符合Weibull概率函数分布，并推导了钢绞线损伤演化方程［8］.

由于钢丝绳的内部空间螺旋结构的复杂性，钢丝绳股内钢丝的受力情况不易确定.本文根据实际6×7IWS型钢丝绳的各项参数，利用Solidworks建立了钢丝绳的三维模型，通过Solidworks Simulation实现有限元分析，得到钢丝绳在10kN载荷下的应力、应变、合位移的大小和分布情况，并根据应变得到钢丝绳中的声发射累计能量的相对值.

1 钢丝绳模型的建立

有限元法FEA（finite element analysis）是一种利用一系列偏微分方程求解关于场问题的数值方法，它可以用简单的方法简化复杂的问题进行求解，将求解域看成是许多小的互连子域构成，对小单元进行分析，其求解的结果与实际值很接近，得到了广泛的认可.Solidworks机械自动化软件是一个基于特征的参数化实体建模设计工具，它可以创建完全关联的三维实体模型，其参数化的特点为：基于特征、基于约束、数据相关、尺寸驱动设计修改［9-10］.由于将 Solidworks中建立的模型导入ANSYS有限元分析软件中会出现多线等几何特征改变的情况，对有限元分析结果造成影响，而Solidworks中集成的Solidworks Simulation可以对Solidworks中建立的几何模型进行分析，可以满足有限元分析的要求.因此，本文中钢丝绳的建模和仿真通过结合Solidworks和Solidworks Simulation来实现.

本文选用缠绕方式较为简单的6×7IWS型钢丝绳，单股6×7IWS型钢丝绳的规格参数如下：股内钢丝直径为3mm，钢丝绳的直径为9mm，股内钢丝捻距为54mm，钢丝捻距为81mm，钢丝绳弹性模量为1.9×1011Pa，泊松比为0.3.在Solidworks中建立钢丝绳的三维模型，确定基准面，通过定义螺旋线的半径、螺距、圈数、扫描轮廓等参数并对其进行扫描，建立的有限元模型如图1.

图1 钢丝绳的有限元模型Figure 1 Finite element model of wire rope

假设钢丝绳有限元模型是各向同性的线性弹性体，进入Solidworks软件中的Simulation，定义钢丝绳的材料为AISI 316退火不锈钢，其材料参数与钢丝绳的参数相同，对钢丝绳有限元模型拉伸过程中边界条件作如下简化处理：在钢丝绳有限元模型的下端面采用夹具固定几何体进行约束，对钢丝绳有限元模型的x、y、z三个方向的自由度进行约束，在另一端面钢丝绳施加轴向10kN的集中载荷.截取180mm绳段对三维模型进行网格划分，划分后其单元数为64980，节点数为118501，自由度为354618，图2为钢丝绳有限元模型受约束、载荷及网格划分方式.

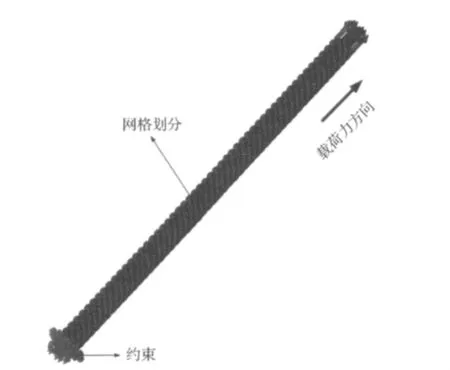
图2 有限元模型的约束、载荷及网格划分Figure 2 Constraint，loading and meshing of the finite element model

2 钢丝绳模型计算结果及讨论

等效应力σd是指在复杂应力状态下，将应力组合与单向拉伸时应力状态的屈服极限相比较，来衡量材料屈服状态的一个物理量［11］，其表达式为：

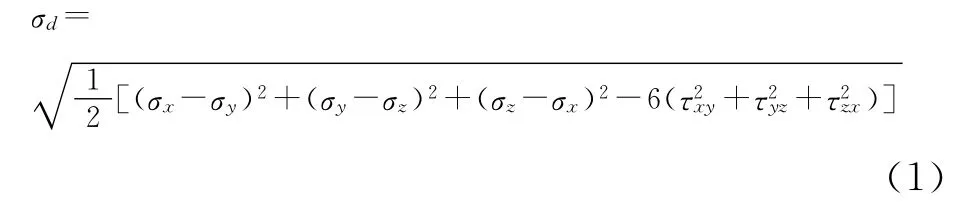
式（1）中，σx、σy、σz分别为沿x、y、z轴向的拉伸应力，τxy、τyz、τzx分别为垂直于截面xoy、yoz、zox方向的剪切应力，当等效应力等于屈服极限时，材料进入塑性变形状态.合位移为钢丝绳模型在三维空间内x、y、z方向上的位移的矢量和，合位移表示如下：

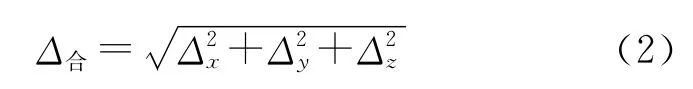
式（2）中，Δx、Δy、Δz分别表示x、y、z方向上的位移.应变在力学中定义为一微小材料元素承受应力时所产生的单位长度变形量，为机械零件和构件等物体内任一点（单元体）因外力作用引起的形状和尺寸的相对改变，常以百分数（%）表示，无量纲，符号为ε.

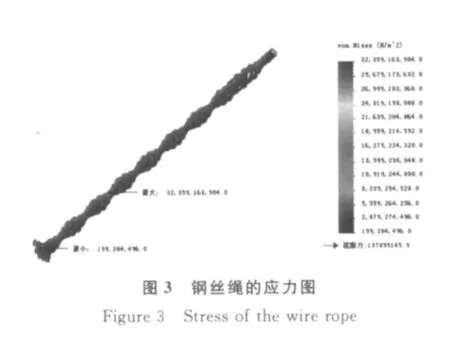
图3、4、5分别为钢丝绳受拉力作用情况下的应力图、合位移图和应变图.由图3可知，应力最小为199284496N／m2，位于钢丝绳下端面约束部分；应力最大为32359163904N／m2，位于距离钢丝绳约束端面约53mm处.合位移沿着施加载荷的方向而增大，合位移最大为35.76552mm，且合位移在靠近施加载荷端比约束端的变化率要大，外侧钢丝的合位移大于内侧钢丝的合位移，这是由于钢丝绳螺旋捻制的缠绕方式决定的.

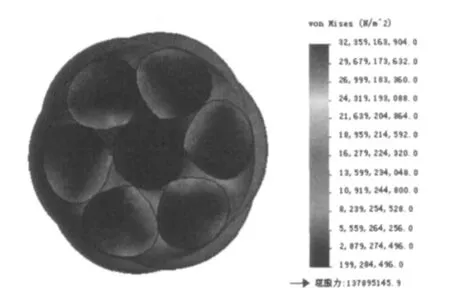
图6 钢丝绳上视面截面图Figure 6 Sectional view of the wire rope from the top

图6为钢丝绳应力的垂直于轴向的一个截面图.从图6中可以看出，钢丝绳股中应力以轴心近似中心对称，其应力以钢丝绳股中丝间接触部分更为显著.在载荷的作用下，外围的六股钢丝略有变形，这是由于在拉伸情况下，钢丝绳股中丝间接触部分的接触应力、摩擦应力造成的.最小等效应力为199284496.0N／m2，屈服力为137895145.9 N／m2，最小等效应力大于屈服力，因此钢丝绳在此情况下为塑性变形.钢绞线塑性阶段的信号主要来源于钢绞线材料的塑性变形，本文中所研究的10kN载荷下，钢丝绳进入塑性变形阶段，此阶段钢丝绳的损伤快速发展，声发射的能量累计值增长加快，钢丝绳的塑性变形会产生声发射信号［12］.这与图6仿真的结果吻合，且图6可以直观地观察出此塑性变形阶段信号产生的位置以及钢丝绳结构的变化，此时钢丝绳拉伸会有一定的声发射活性，能产生声发射信号.

图7 钢丝绳右视面应力图Figure 7 Sectional view of the stress from the right

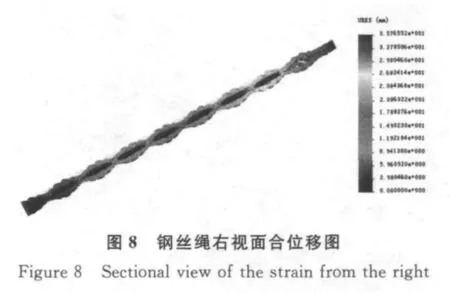
图7、8、9分别为应力、合位移、应变的右视面截面图.从图7、8、9中可以看出，钢丝绳中应力、应变、合位移在空间上沿钢丝绳中心轴呈近似对称，钢丝绳外层的钢丝的位移大于中间层钢丝的合位移，钢丝绳载荷端的位移大于固定端的位移.在进行钢绞线拉伸试验时，通过试验数据发现，声发射的累计能量与拉伸荷载成正比，钢绞线在外部施加载荷的情况下，内部会产生大量的微观缺陷，这些缺陷在钢绞线承受载荷情况下形成、扩展、汇合使得钢绞线的性能逐渐劣化直至破坏.假设钢绞线的损伤都是连续的，材料各微元部分服从Weibull概率分布.Weibull概率分布适用于描述材料的损伤变化过程［8，13-18］，其表示如式（3）：

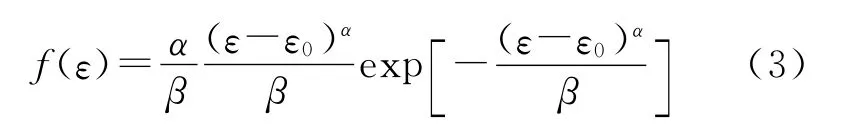
对式（3）两边进行积分，得到服从Weibull函数分布的钢绞线的拉伸损伤演化方程，其表达式为：

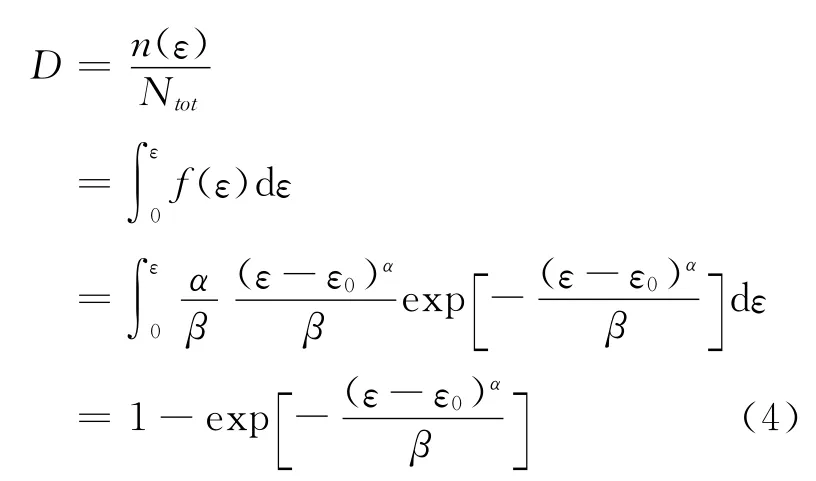
式（4）为采用声发射累计能量相对变化定义的钢绞线拉伸损伤演化模型的表达式，其中D表示钢绞线的损伤因子，ε表示应变，ε0为试验确定的常数，主要与材料初始形态有关，α和β分别为与材料尺寸和变形特性有关的参数，n（ε）和Ntot分别表示在应变值为ε下的声发射的能量值以及钢绞线临界断裂情况下的声发射的总能量，ε0、α、β均可通过对实际拉伸试验时的数据进行回归分析得到.本文研究了根据应变计算声发射累计能量相对值的可行性，由于 Weibull概率分布适用于描述材料的损伤变化过程，所以Weibull概率分布同样适用于本文的钢丝绳拉伸演化模型.材料不同表达式中的各参数也不同，表达式中的各参数有待通过进一步试验回归分析得到，各参数确定后，将所得到的应变最大值0.1051021，最小值0.00118006，代入式（4）可以得到钢丝绳中的声发射累计能量的相对值，该值可以间接的反映钢丝绳的声发射过程中的累计能量.

3 结 语

在钢丝绳中由于螺旋捻制的缠绕方式，其声发射信号的产生和传播是一个复杂的过程.本文通过有限元分析的方法，研究了钢丝绳在载荷作用下的力学性能，确定了钢丝绳拉伸过程中沿轴向应力、应变、合位移的大小及分布情况，定量分析了在10kN的载荷下，应变ε最大值为0.1051021，最小值为0.00118006，根据应变可以得到钢丝绳中的声发射累积能量的相对值，损伤因子能作为间接反映钢丝绳声发射特征的一个重要参数.

［1］谭继文.钢丝绳安全检测原理与技术［M］.北京：科学出版社，2009：10－15.

［2］邵永波，于大安，王 师.声发射技术在钢丝绳失效测试中的应用［J］.无损探伤，1998（3）：4－7.Shao Yongbo，Yu Daan，Wang Shi.Acoustic emission technique in wire rope failure test［J］.NDT，1998（3）：4－7.

［3］李孟源，尚振东，蔡海潮，等.声发射检测及信号处理［M］.北京：科学出版社，2010：24－26.

［4］袁 方，胡斌梁，周知进.在役钢丝绳缺陷检测方法的研究现状与展望［J］.机械设计与制造，2010（2）：260－262.Yuan Fang，Hu Binliang，Zhou Zhijing.An analysis on the research status quo and prospects of defect detection methods of wire ropes［J］.Machinery Design and Manufacture，2010（2）：260－262.

［5］邵永波，朱祖铭，尹万全，等.基于声发射测试的钢丝疲劳损伤过程［J］.钢铁，2000，35（3）：52－55.Shao Yongbo，Zhu Zuming，Yin Wanquan，et al.Fatigue damage of steel wire by acoustic emission monitoring［J］.I－ron and Steel，2000，35（3）：52－55.

［6］邵永波，裴 珍，朱祖铭，等.基于声发射技术的钢丝绳断丝模式识别［J］.应用声学，1999，18（1）：1－5.Shao Yongbo，Pei Zhen，Zhu Zuming，et al.Pattern recognition for wire breakage detection of a steel rope by acoustic emission techniques［J］.Applied Acoustics，1999，18（1）：1－5.

［7］邵永波，于大安，王 师，等.制绳钢丝疲劳测试声发射检测去噪方法［J］.物理测试，1998（6）：21－24.Shao Yongbo，Yu Daan，Wang Shi，et al.The method of noise elimination for acoustic emission detection of steel wire during fatigue test［J］.Physics Examination and Testing，1998（6）：21－24.

［8］李冬生，欧进萍.钢绞线拉伸过程中的声发射特征及其损伤演化模型［J］.公路交通科技，2007，24（9）：57－60.Li Dongsheng，Ou Jinping.Acoustic emission characteristics and damage evolution model of steel strands in tensile test［J］.Journal of Highway and Transportation Research and Development，2007，24（9）：57－60.

［9］李翔鹏.无师自通Solidworks 2008中文版［M］.北京：人民邮电出版社，2008：2－10.

［10］陈超祥，叶修梓.SolidWorks＠Simulation基础教程［M］.北京：机械工业出版社，2010：12－30.

［11］马 军，葛世荣，张德坤.钢丝绳三维接触模型及丝间应力分布研究［J］.中国机械工程，2012，23（7）：864－868.Ma Jun，Ge Shirong，Zhang Dekun.Research on three－dimensional contact model and stress distribution between wires of steel strand［J］.China Mechanical Engineering，2012，23（7）：864－868.

［12］邓 扬，丁幼亮，李爱群，等.基于声发射速率过程理论的钢绞线损伤演化试验研究［J］.东南大学学报：自然科学版，2010，40（6）：1238－1242.Deng Yang，Ding Youliang，Li Aiqun，et al.Experimental study on damage evolution of steel strands based on a－coustic emission signals and rate process theory［J］.Journal of Southeast University：Natural Science Edition，2010，40（6）：1238－1242.

［13］谢志龙，扶名福，闫小青，等.ST13板材声发射参数与应力—应变耦合关系的研究［J］.力学季刊，2012，33（1）：10－14.Xie Zhilong，Fu Mingfu，Yan Xiaoqing，et al.Research on coupling relation between acoustic emission parameter and stress－strain of ST13plate［J］.Chinese Quarterly of Mechanics，2012，33（1）：10－14.

［14］马 军，葛世荣，张德坤，等.钢丝绳股内钢丝的载荷分布［J］.机械工程学报，2009，45（4）：259－264.Ma Jun，Ge Shirong，Zhang Dekun，et al.Load distribution on the unit of the wire rope strand［J］.Journal of Mechanical Engineering，2009，45（4）：259－264.

［15］王 强，张光新，周泽魁，等.基于声发射的输油管线破坏点定位方法研究［J］.浙江大学学报：工学版，2005，39（3）：322－325，329.Wang Qiang，Zhang Guangxin，Zhou Zekui，et al.Research on acoustic emission location method for oil pipelinebreakage［J］.Journal of Zhejiang University：Engineering Science，2005，39（3）：322－325，329.

［16］姜海波.矿用提升钢丝绳数值建模及有限元分析［J］.煤矿机械，2011，32（1）：96－98.Jiang Haibo.Model build and finite element analysis of wire rope［J］.Coal Mine Machinery，2011，32（1）：96－98.

［17］刘鑫磊，袁昌明，王 强.混凝土结构健康检测的声发射圆阵波束形成仿真分析［J］.中国计量学院学报，2011，22（1）：34－38，67.Liu Xinlei，Yuan Changming，Wang Qiang.The simulation analysis of acoustic emission circular array beamforming for concrete structural health monitoring［J］.Journal of China Jiliang University，2011，22（1）：34－38，67.

［18］金 挺，孙 智，孙利民.裂缝扩展声发射有限元模拟及其信号时频分析［J］.振动、测试与诊断，2007，27（4）：288－291.Jin Ting，Sun Zhi，Sun Limin.Modeling of acoustic emission due to crack growth with finite element method and time－frequency analysis of the signal［J］.Journal of Vibration，Measurement and Diagnosis，2007，27（4）：288－291.