霍尔效应的地下位移三维测量方法研究

周 振，李 青，池金谷，李 雄，杜通波

（中国计量学院 机电工程学院，浙江 杭州 310018）

滑坡一般指由于受到地质结构、地表或地下水活动、人工切坡等因素的影响，斜坡上的部分岩体和土体沿地层软弱面（或软弱带）在重力作用下向下滑动的不良地质现象［1-2］.国际上采用 Varnes提出的五种运动类型来对滑坡进行分类：崩塌，倾倒，滑动，侧向扩展和流动［3-4］.美国地质调查局（USGS）于2004年进一步细分，包括：旋转型滑坡，平移型滑坡，块体滑坡，岩崩，弯折倾倒，碎屑流，碎屑崩塌，泥土流动，蠕滑和侧向扩展.

滑坡的监测内容包括地表位移、地下位移、地下水位、地下推力、土壤湿度、位移速率、地下水压力、地应力等，其中地下位移的监测是重点也是难点.国内外对于坡体深部位移监测主要利用埋设在地质钻孔中的测斜仪［5-6］、多 点 位 移 计［7-9］和TDR同轴电缆［10-13］来获取数据.钻孔测斜仪不能测量滑坡体不同深度的垂直位移；多点位移计只能测量一维位移；TDR监测技术很难确定滑坡滑动的方向，且同轴电缆的伸缩性很差；三种主流测量方法都不能测量出地下位移的三维变化，而只有三维变化的测量才能真正反应出地下岩土的实际变化情况.鉴于此，笔者提出一种基于霍尔效应的地下位移三维测量方法.

1 工作原理

旋转型滑坡、平移型滑坡和块体滑移是常见的滑坡类型，旋转型滑坡示意图如下：

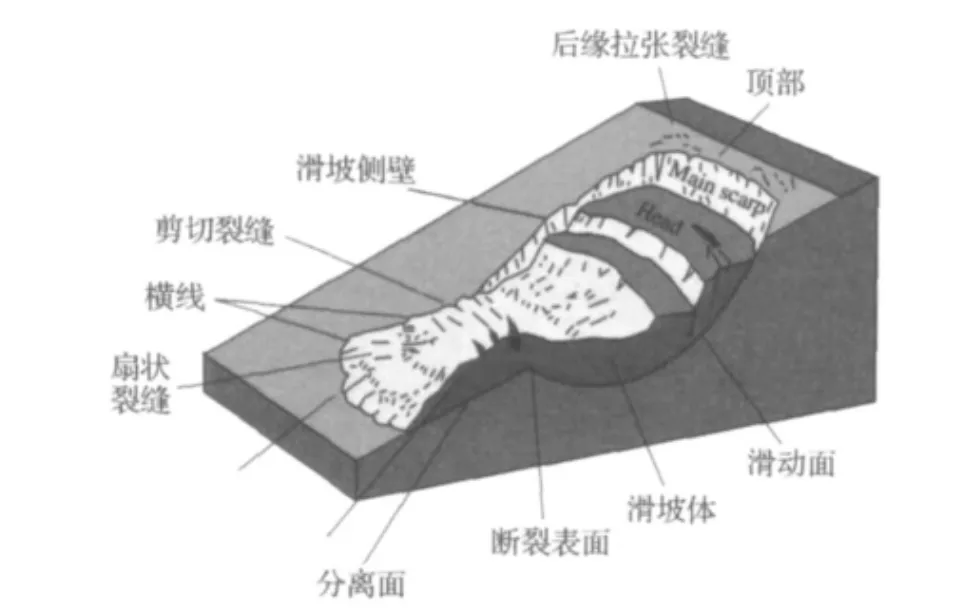
图1 旋转型滑坡Figure 1 Rotational landslide

旋转型滑坡是指沿着向上凹的弧形破裂面滑动的滑坡，滑坡移动只沿内部滑面发生，坡体裂缝在平面上呈环状且凹向移动方向，其下伏破裂面连同外露破裂壁呈勺形，滑坡的坡体移动时近似绕平行于斜坡的轴转动［14］.

平移型滑坡和块体滑移的示意图如图2.

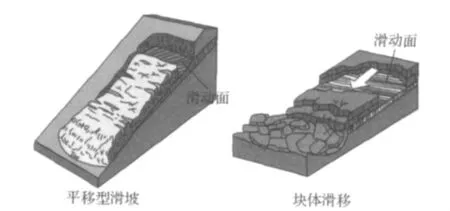
图2 平移型滑坡和块体滑移Figure 2 Translational landslide and block slide

对旋转滑坡的地下位移测量需要同时测量出水平及垂直位移，这就要求测量方法能实现三维测量.本文提出的基于霍尔效应的地下位移三维测量方法，其工作原理如图3.

图3中的测量单元均为圆柱体，内置传感器及电路.各个测量单元通过电源线、信号线连成一串与主机相连，且各个测量单元之间用高弹性连接物相连.在实际安装过程中，保持各个测量单元的上下平面平行，并找到地下岩层的不动层，将一个测量单元埋入其中作为基准，建立三维坐标系.

当最复杂的多级旋转型滑坡发生时，每一个滑坡坡体移动近似绕平行于斜坡的轴转动，且每一个滑坡坡体基本保持原样.这样，坡体的运动将改变各个测量单元之间的相对位置，且相邻测量单元之间的上下表面基本保持平行.如图4.

只要能测量出各个测量单元之间的相对位置变化，并以埋入不动层中的测量单元为基准，就可以测量出整个地下岩土的三维变化情况.类似的测量思想可以在很多文献中得到佐证，并有大量的实际应用项目支持，笔者所在的科研团队对此相关领域已有多年的研究［15-16］.能否完成三维测量，关键在于如何测量出各个测量单元之间的相对位置变化.基于霍尔效应设计集成式传感器并配合相应的算法，就可实现这一目的.

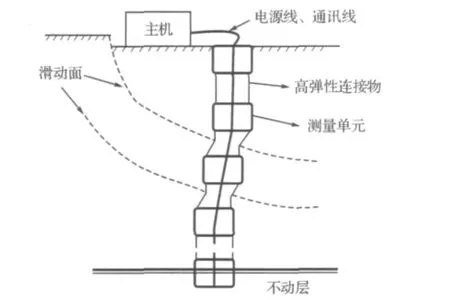
图4 滑坡示意图Figure 4 Schematic plan of landslide

霍尔效应：当电流垂直于外磁场通过导体（或半导体）时，在导体（或半导体）的垂直于磁场和电流方向的两个端面之间会出现电势差.可用如下公式表示：

式（1）中，RH为霍尔系数；I为通过的电流；B为垂直于I的磁感应强度；d为导体的厚度.当电流I和霍尔片的厚度d保持不变时，霍尔电势差UH与磁感应强度B成正比.通过电势差UH即可反映磁感应强度的变化［17］.

在本方案中，磁场来源为圆柱形钕铁硼永磁体.当磁钢与霍尔传感器的相对位置发生变化时，霍尔传感器的输出电压就能指示出具体的变化情况.

2 设计方案

本文提出的测量方法，核心内容是传感器的设计以及所采用的测量算法.

什么是发展？列宁曾认为，有两种基本的(或可能的？或两种在历史上常见的？)发展(进化)观点：一种观点认为发展就是减少和增加，是重复，另一种观点认为发展就是对立面的统一。也有学者从哲学视角分析，认为发展是指事物由小到大、由简单到复杂、由低级到高级的变化。还有人认为发展指变化的趋势。一般说来，发展的内涵包括自然的演化和人类社会的进步，是指事物自身的矛盾运动和空间相互作用和时间序列的永恒历史运动。发展是人类社会的永恒主题，也是人类文明演进的逻辑起点。

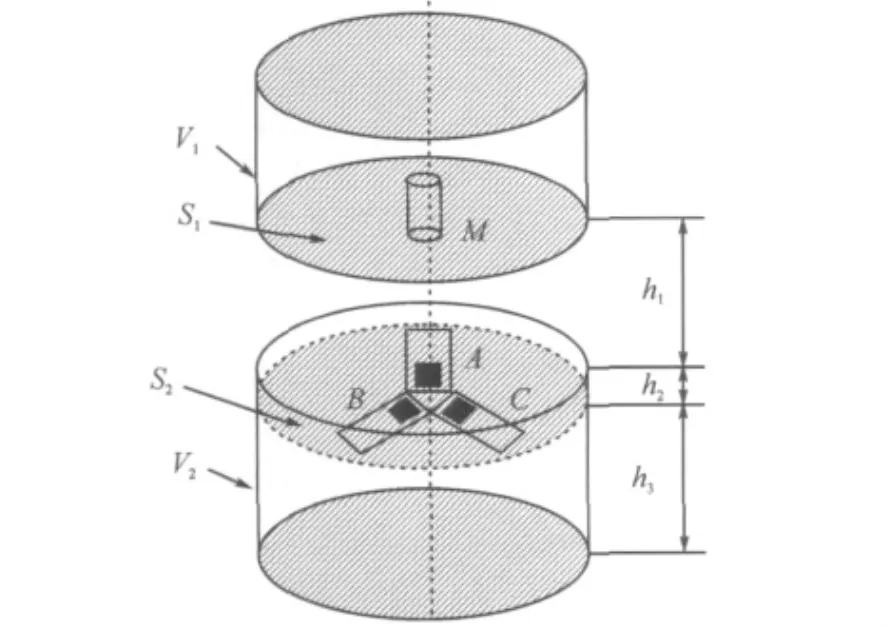
图5 传感器结构Figure 5 Sensor structure

图5中，传感器分为两个部分.第一部分是空心圆柱体V1，一块圆柱形钕铁硼永久磁钢M（φ5×h18，单位mm）固定在其下端面面板S1上.第二部分是空心圆柱体V2，在距离其上端h2（13.5mm）的面板S2上，是由三个水平紧密贴合的霍尔传感器组成的阵列，如图6.霍尔传感器陶瓷片的中心点可感受磁感应强度，三个霍尔传感器陶瓷片的中心点构成一个等边三角形的三个顶点A、B、C，边长L为12mm.

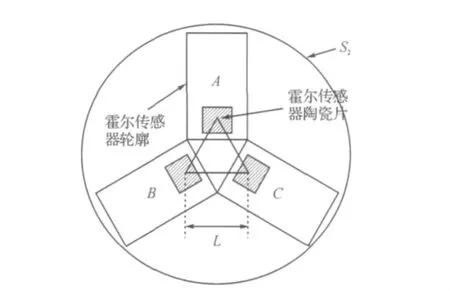
图6 面板S2俯视图Figure 6 Plan view of panel S2

这里将空心圆柱体V1与V2相隔h1，是为了便于观察.在实际测量中，只需将两者贴合即可.在进行岩土地下三维位移测量时，将空心圆柱体V1埋入岩土滑动层，V2则埋入岩土不动层.当地下土层发生相对位移时，就可以测量土层的三维位移情况.如果增加圆柱体V1与V2的数量，连成葫芦串，就可测量大厚度土层的三维位移情况.

进行如图7的磁钢位移标定实验.为配合实验，搭建如图8的测量系统.

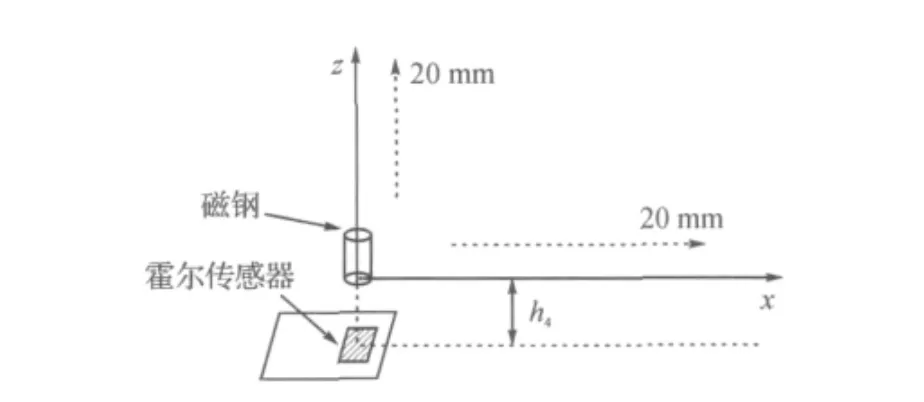
图7 位移实验Figure 7 Displacement experiment

图8 测量系统Figure 8 Measurement system

本文设计的标定和测试实验是在7SC405高精度五轴运动台上进行的.将霍尔传感器的位置固定，并将磁钢固定在7SC405运动台的运动臂（非金属材质）上.通过上位机控制运动台的动作，精确改变磁钢与传感器之间的相对位置.图7中，以霍尔传感器陶瓷片中心点正上方h4（13.5mm）处为坐标原点，建立xz直角坐标系.z轴垂直于霍尔传感器所在平面，且经过陶瓷片中心点.x轴平行于霍尔传感器所在平面.

首先，让圆柱形磁钢下端面的中心点与坐标系原点重合，然后使之水平向右移动.每次移动0.2mm，采集霍尔传感器输出的电压值，一共移动100次.然后，让磁钢回到坐标系原点，并增加高度0.2mm，重复同样的实验.接着，重复前两步的实验.整个实验将得到一个100行100列的二维数组.利用MATLAB进行三维绘图，如图9.

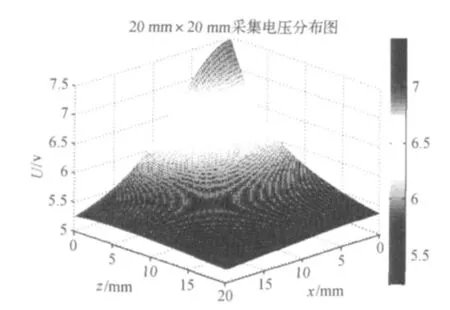
图9 电压采集分布图Figure 9 Distribution map of sampled voltage

当磁钢逐渐远离霍尔传感器，无论是沿着x轴方向或是z轴方向，传感器输出电压都将相应减小.在x轴及z轴坐标最小处，传感器输出电压达到最大值.相反，在x轴及z轴坐标最大处传感器输出电压最小，因为此时霍尔传感器与钕铁硼永磁体之间的相对距离最大.对图9进一步处理，利用MATLAB绘制等高线，每一条等高线代表相同的电压值，且相邻两条等高线之间的差值是相同的，如图10.图10中可以看到，等高线基本上是单调递减的.

图10 15条等高线分布图Figure 10 Distribution map of 15contour lines

回顾之前的位移标定实验，可以得出这样的结论：当磁钢在一条等高线上移动时，霍尔传感器输出的电压将不会改变.由于磁钢是圆柱体，且沿着中轴线被磁化，那么其磁场应该是关于它的中轴线对称分布的.将等高线绕着z轴旋转一圈，可以得到一个三维等值曲面.当磁钢在这个等值曲面上移动时，霍尔传感器输出的电压值不变.再看之前的传感器俯视图（图6），当磁钢处在霍尔传感器阵列所在平面的上方时，三个霍尔传感器将输出三个电压值.根据之前所述的磁钢位移标定实验，依据每一个电压值可以得到相应的等值曲面.两个等值曲面相交得到一条曲线，这条曲线与第三个等值曲面相交就能得到一个唯一交点，交点的三维坐标就是磁钢下端面中心点的坐标.

以上阐述了此测量方法在理论上的可行性.理想的交点计算方法是利用三条空间曲线直接计算求取交点，这三条空间曲线分别对应于三个等值曲面.但从MATLAB中能提取的仅仅是等高线上离散点的坐标，并不是等高线的函数表达式.由于对离散点采用曲线拟合的方法获得函数表达式，其误差较大，故不妨换一个角度思考问题：假设已经得到能够准确表达等高线的函数表达式，用一个平行于xy平面的切面横切上文中提到的三个等值曲面，那么一定能得到三个圆.设三个等值曲面交点的坐标是（x0，y0，z0），则必定会有一个切面z＝z0，使得此切面横切出来的三个圆能交与一点，这个点就是所要求的交点.前文述及构成一条等高线的是一簇离散点，那么将相邻的两个离散点全部用直线相连就能得到一条折线.将此折线同样绕着z轴旋转一圈，也能得到一个等值曲面，只是这个等值曲面并不光滑.用一个切面z＝z1去横切三个这样的等值曲面，也能得到三个圆.当z1足够接近甚至是等于z0时，能确保横切出来的三个圆当中，有两个圆相交于两点.当然，无论这两个点当中的哪一个点与第三个圆圆心之间的距离都可能不等于第三个圆的半径，但只要两者相差的值小于某个设定值，就可以认为三个圆能交与一点，由此也就计算出了三个等值曲面的交点.实际操作中，利用 MATLAB得到40条等高线对应的离散点的坐标，存储在软件中.当需要用到某个特定电压对应的等高线时，就利用软件插值去求取相应的离散点的坐标.

图10所描绘的是20mm×20mm磁钢位移标定实验中，霍尔传感器输出电压的等高线簇.由于是软件插值，可以无限增加等高线簇的密度，即近似地认为等高线簇构成了一个面.将这个面绕着z轴旋转一圈，就能得到一个圆柱体（φ40×h20，单位mm）.如图6，三个霍尔传感器的排列呈一个等边三角形.三个传感器对应三个这样的圆柱体，三个圆柱体在三维空间中相交得到一个立体图形，如图11.图中的柱体描绘了测量的空间范围，高为20mm，其上下底面如图12（图中灰区域）.也就是说，只要磁钢下端面的中心点处在这个柱体中，就能测量出其所处位置的三维坐标.

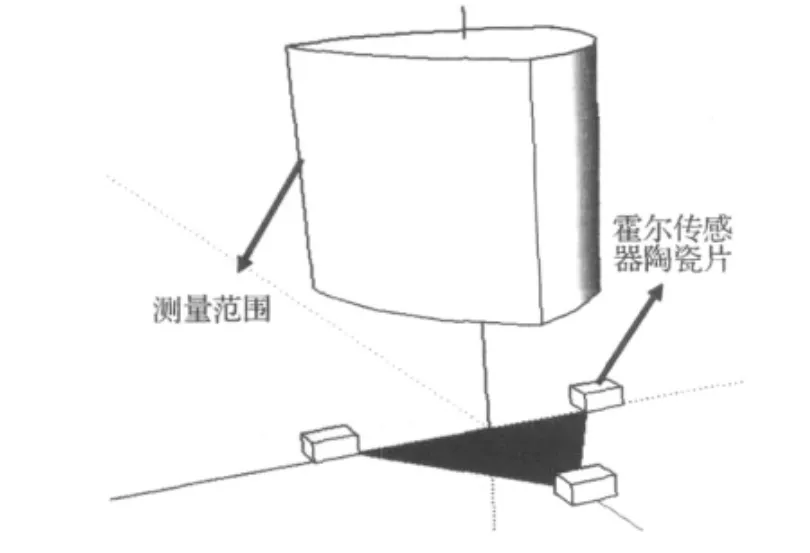
图11 测量范围的三维视图Figure 11 3Dview of measurement range

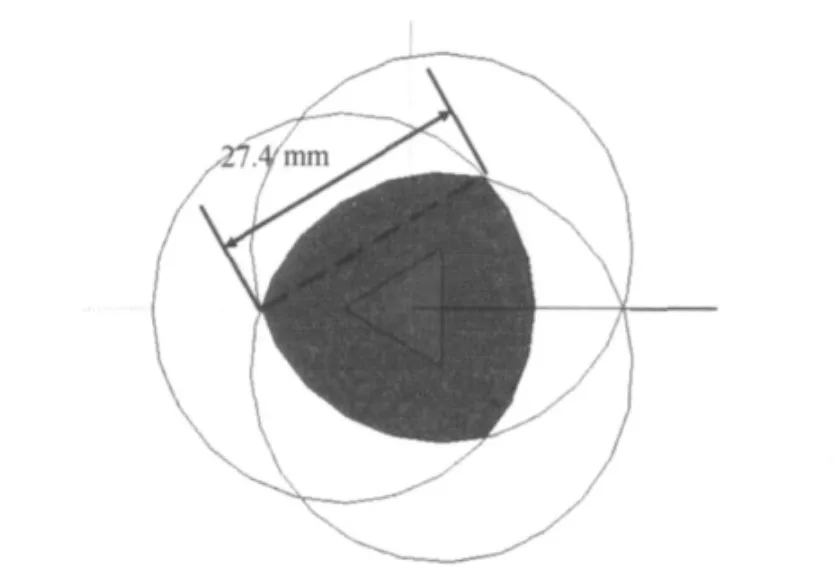
图12 柱体的底面Figure 12 Underside of the cylinder

将测量装置埋入岩土深部以后，测量出此时磁钢下端面中心点处的三维坐标（x1，y1，z1），也就是起始点坐标.当土层发生形变，可测量出形变之后的坐标值（x2，y2，z2）.通过简单的几何运算可以得到垂直及水平的位移大小值，也可以采用公式（2）得出总位移的大小.

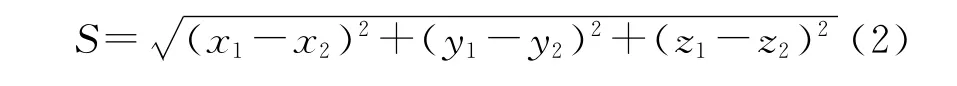
3 数据分析

建立图13的系统三维笛卡尔坐标系：

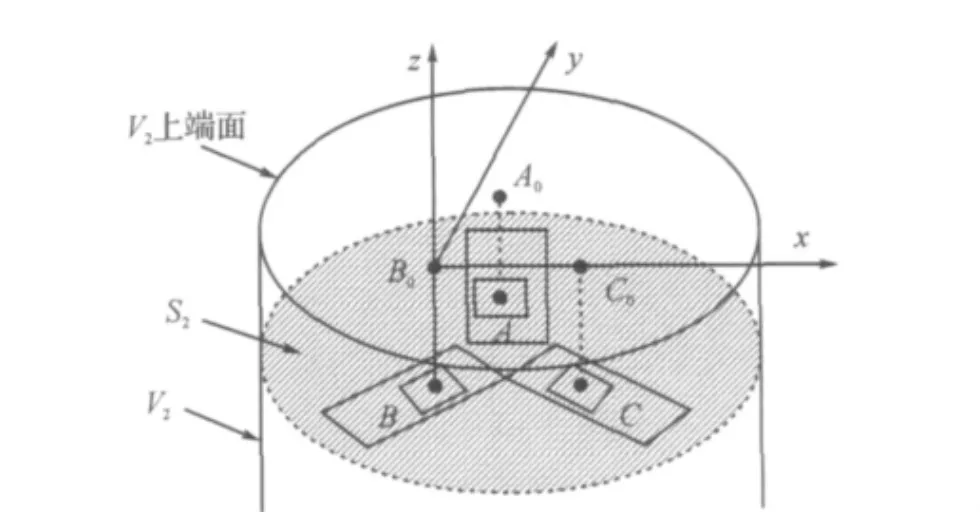
图13 测量装置系统坐标系Figure 13 Coordinate system of the measurement equipment

三个霍尔传感器陶瓷片的中心点A、B、C在V2上端面上的投影为A0，B0，C0.以B0点为三维笛卡尔坐标系的原点，x轴沿着线段B0C0水平向右，y轴同处在V2上端面且垂直于x轴，z轴垂直xy平面向上.实际制作的测量装置，B点的坐标为（0，0，－13.5），C 点的坐标为（12.325，0，－13.5），A 点的坐标为（5.95，11，－13.5），单位mm.选取一个8mm×8mm×8mm区域进行测量，一共216个点.其中x轴坐标分别取为2.1625、3.7625、5.3625、6.9625、8.5625、10.1625，y轴和z轴坐标分别取为0、1.6、3.2、4.8、6.4、8.

测量结果显示，有些点的x轴坐标的测量误差能达到0.5mm，y轴、z轴坐标误差较小.造成这种现象的一个原因是：图10中的等高线是基本单调递减的，而且等高线的起始段是趋向于水平的.起始段上的两个点（x1，y1）、（x2，y2），差值y2－y1远小于差值x2－x1.实际测量时，由于时漂以及温漂等因素的影响，电路测得的霍尔传感器的输出电压会有微小的偏差.这个偏差的影响相当于对等高线造成了y2－y1的差值，反应在测量结果上就是x坐标的测量误差较大.进行多次测量，对误差进行分析，得出非常相似的规律，由此表明，算法仍需改进.利用这些规律，结合实验数据，采用优化算法中的麦夸特法＋通用全局优化法进行拟合，得到三个坐标各自的补偿值的计算公式.拟合模型均采用如公式（3）的形式：

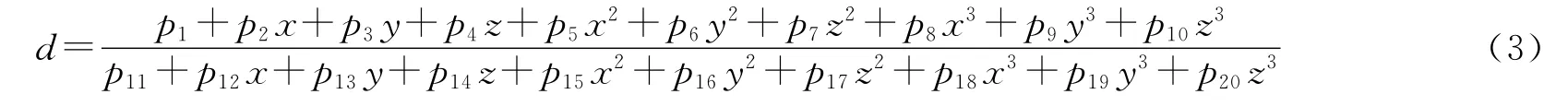
式（3）其中d为补偿值，分别有dx、dy以及dz，对应三个坐标轴.p为常量，x、y、z均为初步测得的未经补偿的坐标值.将初步测得的值减去补偿值就得到了最终的测量值.选取一次实验，代入216个点的数据进行拟合.三条拟合公式的残差平方和均小于0.21，相关系数均大于0.95.x坐标的补偿值较大，最大能接近0.4mm，y、z坐标的补偿值较小.这里只将补偿值dx计算公式的常量p罗列如下：35.38，－1.28，－1.86，－3.52，0.718，－0.436，2.64，－0.057，0.036，－0.182，72.142，6.07，－8.1，－5.155，－0.013，－0.328，3.491，－0.0288，0.0324，－0.265.将得到的三条补偿公式去修正另几次实验的测量结果，效果较好.进行一次新的实验，并加入补偿公式进行校准，一共测量216个点，x轴坐标分别取为2.1625、3.7625、5.3625、6.9625、8.5625、10.1625，y轴和z轴坐标分别取为0、1.6、3.2、4.8、6.4、8.图14表示的是x坐标测量的情况，216个点中x坐标为2.1625的一共有36个点，其他五种取值同理.

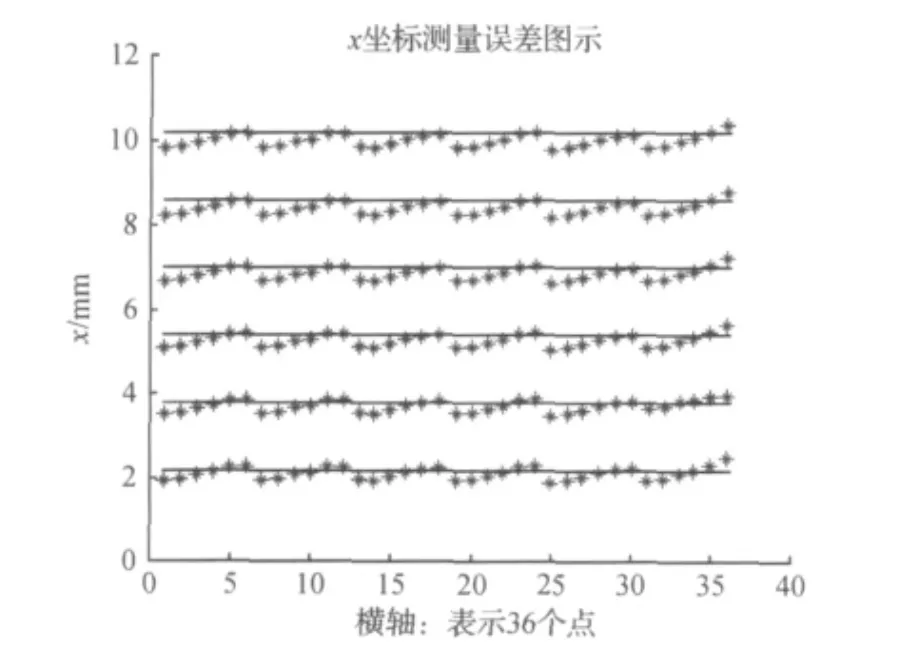
图14 x坐标测量Figure 14 x－coordinate measurement

图中横坐标表示第1到第36个点，纵坐标表示x坐标值.星点表示最终测量的坐标值，黑线表示实际的坐标值，两者的差值就是实际测量的误差.同样地，y轴及z轴坐标的测量误差如图15、图16.

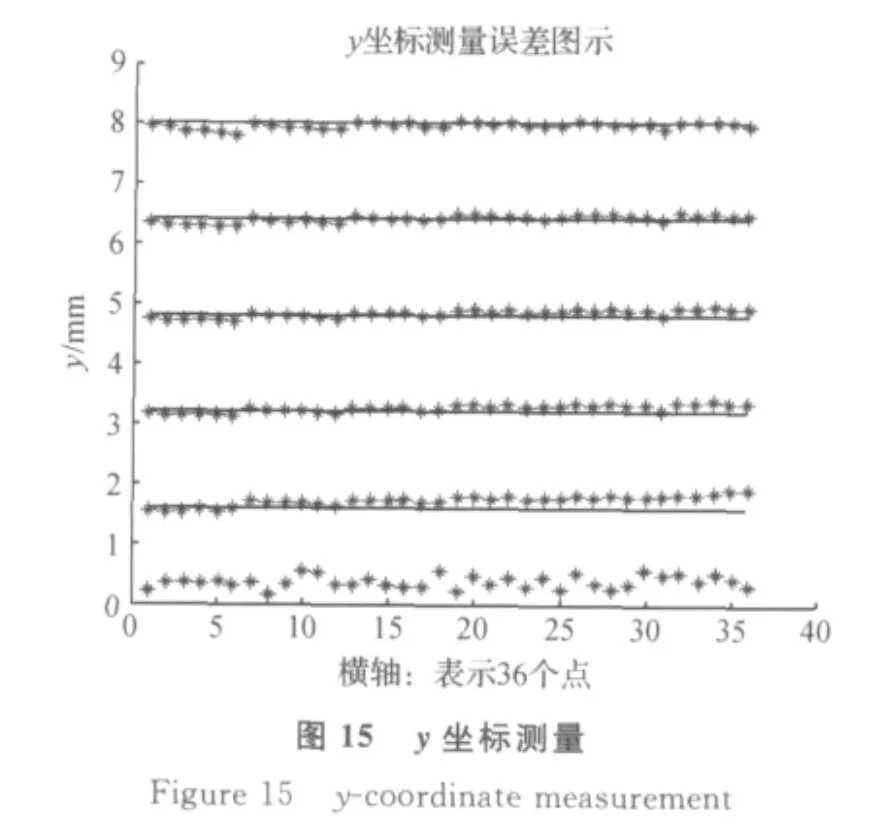
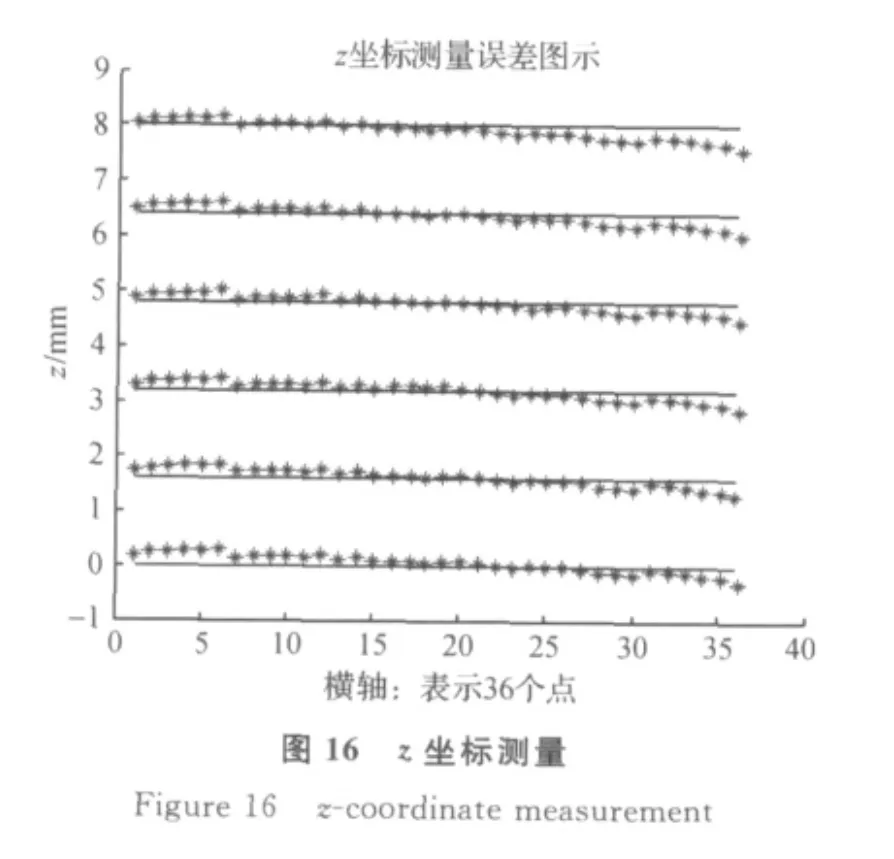
由于磁钢产生的磁场分布非线性，空间中不同区域的点的测量精度是不同的，这点可以在图形中反应出来，即误差有大有小.

4 结 语

土体的运动将改变传感器与磁钢之间的相对位置，采用上述方法可计算出土体变形前后磁钢的三维坐标，通过简单的几何运算就可以得到位移的大小值.本方案设计的三维位移测量方法能较全面地测量地下土层的形变情况，并达到一定的测量精度，从而为地质灾害地下位移监测提供了一种新的解决方案.

［1］仝达伟，张平之，吴重庆，等.滑坡监测研究及其最新进展［J］.传感器世界，2005，11（6）：10－14.Tong Dawei，Zhang Pingzhi，Wu Chongqin，et al.Research and new development of landslide activity monitoring［J］.Sensor World，2005，11（6）：10－14.

［2］董勖壮.浅谈滑坡成因及防治措施［J］.矿业工程，2009，7（1）：8－11.Dong Xunzhuang.Analysis of reasons for hill creep and its prevention［J］.Mining Engineering，2009，7（1）：8－11.

［3］Varnes D J.Slope movement types and processes［C］／／National Research Council.Washington，DC：［s.n］，1978：11－33.

［4］Schuster R L，Krized R J.Landslide Analysis and Control［M］.Washington，DC：National Academy of Sciences，1978：5－10.

［5］王翠珀，李继涛.钻孔测斜仪在某露天矿深层岩移监测中的应用［J］.山西建筑，2010，36（14）：91.Wang Cuipo，Li Jitao.The clinograph application in an open pit mine deep rock movement monitoring［J］.Shanxi Architecture，2010，36（14）：91.

［6］张丽芬，姚运生，曾夏生，等.钻孔测斜仪在高台滑坡深部位移监测中的应用［J］.地质灾害与环境保护，2007，18（4）：91－94.Zhang Lifen，Yao Yunsheng，Zeng Xiasheng，et al.Application of CX－03borehole inclinometer to enshi slope monitoring［J］.Journal of Genological Hazards and Environment Preservation，2007，18（4）：91－94.

［7］陈义军，刘长武，徐 进，等.新型套管式同轴多点位移计及其在隧道围岩变形监测中的应用［J］.岩土工程学报，2008，30（7）：1085.Chen Yijun，Liu Changwu，Xu jin，et al.Application of new spigot coaxial rod extensometer in monitoring deformation of surrounding rock［J］.Chinese Journal Geotechnical Engineering，2008，30（7）：1085.

［8］张乾兵，朱维申，李 勇，等.洞群模型试验中微型多点位移计的设计及应用［J］.岩土力学，2011，32（2）：623－628.Sun Qianbin，Zhu Weishen，Li Yong，et al.Design of mini multipoint extensometer in geomechanical model test of cavern group and its application［J］.Rock and Soil Mechanics，2011，32（2）：623－628.

［9］刘文庆，赵 飞，董建辉，等.多点位移计在高速公路高边坡稳定性监测中的应用［J］.地质灾害与环境保护，2010，21（4）：104－107.Liu Wenqin，Zhao Fei，Dong Jianhui，et al.Application of multiple－point rod extensometer to high slope of high slope of expressway stability monitoring［J］.Journal of Genological Hazards and Environment Preservation，2010，21（4）：104－107.

［10］谭捍华，傅鹤林.TDR技术在公路边坡监测中的应用试验［J］.岩土力学，2010，31（4）：1331－1336.Tan Hanhua，Fu Helin.Testing study of application of time domain reflectometry to highway slope monitoring［J］.Rock and Soil Mechanics，2010，31（4）：1331－1336.

［11］张 青，史彦新.基于TDR的滑坡监测系统［J］.仪器仪表学报，2005，26（11）：1199－1202.Zhang Qing，Shi Yanxin.The landslide monitoring system based on TDR［J］.Chinese Journal of Scientific Instrument，2005，26（11）：1199－1202.

［12］陈云敏，陈 赟，陈仁朋，等.滑坡监测TDR技术的试验研究［J］.岩石力学与工程学报，2004，23（16）：2748－2755.Chen Yunmin，Chen Yun，Chen Renpeng，et al.Testing study on applications of time domain reflectometry to slope monitoring［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23（16）：2748－2755.

［13］Singer J.Development and testing of a time domain reflectometry（TDR）monitoring system for subsurface deformations［C］／／Proceedings of the European Rock Mechanics Symposium.Eurock：［s.n］，2010：613－616.

［14］李 滨，殷跃平，吴树仁，等.多级旋转黄土滑坡基本类型及特征分析［J］.工程地质学报，2011，19（5）：704.Li Bin，Yin Yuepin，Wu Shuren，et al.Basic types and characteristics of multiple rotational landslides in loess［J］.Journal of Engineering Geology，2011，19（5）：704.

［15］杨 杰，李 青.地下位移实时监测系统研究［J］.中国计量学院学报，2008，19（1）：41－46.Yang Jie，Li Qing.On real－time underground displacement monitor systems［J］.Journal of China Jiliang University，2008，19（1）：41－46.

［16］Shentu Nanying，Zhang Hongjian.Research on an electromagnetic induction－based deep displacement sensor［J］.IEEE Sensors Journal，2011，11（6）：1504－1515.

［17］池金谷，李 青.一种基于霍尔效应的岩土地下位移精密测量方法［J］.工业控制计算机，2010，23（6）：63－64.Chi Jingu，Li Qing.Method of precise measurement of underground displacement based on hall effect［J］.Industrial Control Computer，2010，23（6）：63－64.