试题探究三种“境界”——2013年高考江西卷第20题纵向、横向、拓展探究及反思

☉江苏省西亭高级中学 陆王华

2013年高考江西卷第20题为解析几何题，它是一道考查了椭圆的方程、直线与椭圆的位置关系、直线的斜率等知识的综合试题，看似常规，却彰显对常规数学思想方法以及通性通法的运用，突出“淡化层次内的区分，强化层次间的区分”的评价理念，考查了学生综合应用知识及探究问题的能力，值得继续学习与研究.

一、试题呈现

（Ⅰ）求椭圆C的方程；

图1

（Ⅱ）AB是经过右焦点F的任一弦（不经过点P），设直线AB与直线l相交于点M，记PA，PB，PM的斜率分别为k1，k2，k3.问：是否存在常数λ，使得k1+k2=λk3？若存在，求λ的值；若不存在，说明理由.

二、试题探究

1.纵向探究

又因为y1x2+y2x1=2kx1x2-kc（x1+x2），y1+y2=k（x1+x2）-2kc，所以

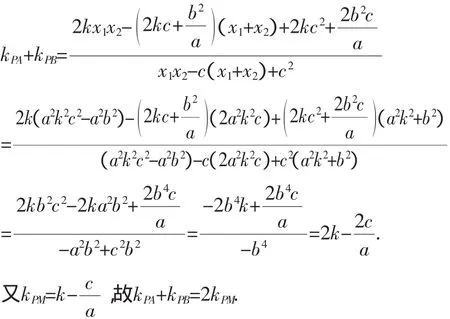
上面的结论中，点F在x轴上，很自然联想到，若将点F改在y轴上，情况如何？

笔者通过探究得到如下结论：

图2

证明：由结论1的证明得

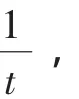
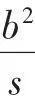
2.横向探究

对于双曲线和抛物线也有类似结论：

据圆锥曲线的对称性，改变焦点F及相应准线的位置，上述结论也同样成立.

于是得到圆锥曲线的一个统一定理：

定理：点P是圆锥曲线E上一点，准线为l，对应的焦点为F，PF⊥x轴，AB是经过焦点F的任一弦（不过P点），设直线AB与准线l相交于点M，记PA，PB，PM的斜率分别为kPA，kPB，kPM，则kPA+kPB=2kPM.

3.拓展探究

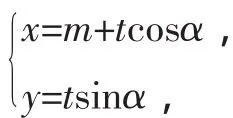
类比可得，双曲线和抛物线也有下面结论：

在平时课堂教学中，我们不仅要得到问题的答案，更要让学生知道问题的一般规律即数学本质.正确认识必然性与偶然性的辩证关系对于学习和研究数学有重要的指导意义.在新课改理念指引下，就是要培养学生透过大量的偶然性的表面现象去揭示其中蕴涵的一般规律，由现象认识本质，由个别到一般，由经验上升为理论，这一点在新课改中显得尤为重要.