例谈任务驱动教学法在数学探究课教学中的应用

☉黑龙江省大庆实验中学 侯典峰 郝明泉

著名心理学家布鲁纳认为：学习是一个主动的过程，对学生学习内因的最好激发是对所学材料的兴趣，积极的思维是建立在深厚的兴趣和丰富的感性基础上的，只有这样，学生才会积极主动地去学习，去思考，去探索知识的奥秘，建构主义指出：任何学习的发生都不是在白纸上进行的，而是将新知识与已有知识建立联系，从内部通过创造、协调对原有经验进行改造和重组，对新知识进行意义构建，建构主义教学设计原则强调：学生的学习活动必须与大的任务或问题相结合；以探索问题来引导和维持学习者的学习兴趣和动机；学生必须拥有学习的主动权，教师不断地激励学生前进.

任务驱动教学法是一种建立在建构主义理论基础上的教学方法，它把学生的学习活动与任务相结合，以探索问题来激发和维持学习者的学习兴趣和动机，让学生紧紧围绕着学习任务，在强烈的问题动机驱动下，在教师的帮助下，对任务进行分析和讨论，通过对学习资源积极主动地占有和应用，进行自主探索和互动协作，通过任务的完成实现对所学知识的意义建构.任务驱动教学法符合探究教学模式，即要求在教学过程中，以完成一个个具体的任务为线索，把教学内容巧妙地隐含在每个任务之中，让学生自己提出问题，并经过思考和老师的点拨，自己解决问题.在完成任务的同时，培养了学生的创新意识、创新能力与自主学习的习惯以及学会如何去发现问题、思考问题、寻找解决问题的方法.因此，任务驱动教学法有利于培养学生的创新能力、分析问题、解决问题的能力.

普通高中《数学课程标准》指出新课程的基本理念第三条是：倡导积极主动、勇于探索的学习方式.

学生的数学学习活动不应只限于接受、记忆、模仿和练习，高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式.这些方式有助于发挥学生学习的主动性，使学生的学习过程成为在教师引导下的“再创造”过程.同时，高中数学课程设立“数学探究”、“数学建模”等学习活动，为学生形成积极主动的、多样的学习方式进一步创造有利的条件，以激发学生的数学学习兴趣，鼓励学生在学习过程中，养成独立思考、积极探索的习惯.高中数学课程应力求通过各种不同形式的自主学习、探究活动，让学生体验数学发现和创造的历程，发展他们的创新意识.数学探究即数学探究性课题学习，是指学生围绕某个数学问题，自主探究、学习的过程.这个过程包括：观察分析数学事实，提出有意义的数学问题，猜测、探求适当的数学结论或规律，给出解释或证明.

在数学探究课中探究课题的选择，即学习的任务的设计是完成探究学习的关键，任务的设计要有助于学生对数学的理解，有助于学生体验数学研究的过程，有助于学生形成发现、探究问题的意识，有助于鼓励学生发挥自己的想象力和创造性.

数学探究课需要教师针对所要学习的内容设计出具有思考价值的、有意义的问题，即布置科学的任务，让学生去思考、去尝试解决.多数同学对任务都会产生一种急切完成的动机，而完成任务又能给他们带来成就感和满足感.通过布置任务，驱使学生由“要我学”变成“我要学”.解决问题往往需要学生思考分析问题的方法，这样，分析的过程就是学生学习的过程，所以任务的设置是非常关键的一环.采用“任务驱动”教学法，关键是“任务”设计，要仔细推敲知识点、统筹兼顾，为学生设计、构造出一系列典型的可操作的“任务”，通过教学实践也充分证明“任务”按照以上设计就能真正让学生动起来.

本文记录了笔者应用“任务驱动”教学法对一道高考题的探究过程，与同行交流.

探究题目 数列{an}满足 an+1+（-1）nan=2n-1，则 an的前60项和为________.

引言 此题是2012年普通高等学校招生全国统一考试理科数学第16题，构思新颖、独特，形式简洁、优美，内容丰富，有较为深刻的内涵，命题角度为一般数列，着重考查数学、思想方法的掌握，考查逻辑推理能力和观察、分析、联想、归纳等思维能力，具有较良好的区分度，内容涉及数列的通项公式，数列的递推公式，数列的前n项和Sn等，有一定的难度和综合度，考场上很多学生做到此题时感到陌生，不知从何下手，仔细回忆头脑中求数列通项公式与数列求和的常见方法和平时积累的一些技巧，尝试后发现均不能奏效，大脑出现空白，出现卡壳现象，特别是一些学习程度较好的平时常能攻克填空压轴题的学生，也出现了对此题求解无能为力的现象.

问题1：此题果真很难求解吗？

任务1 对题目结果进行探究.

探究过程：

利用迭代法，得到如下一些式子，试图从前12项中找到规律但通过前12项的值观察分析，

故若设a1=a，则可得a2=1+a，a3=2-a，a4=7-a，a5=a，a6=9+a，a7=2-a，a8=15-a，a9=a，a10=17+a，a11=2-a，a12=23+a.

角度1：从数列的构成规律来看，着眼于细微.

方法1：先将前12项按以下格式排列，

不难看出：

第1项，第5项，第9项相同，第2项，第6项，第10项是首项为1+a，公差为8的等差数列.

第3项，第7项，第11项相同，第4项，第8项，第12项是首项为7-a，公差为8的等差数列.

于是猜测：数列{an}是由如下子数列构成的：

子数列 1：a1，a5，a9，…是常数数列a；

子数列 2：a2，a6，a10，…首项为 1+a，公差为 8 的等差数列.

子数列 3：a3，a7，a11，…是常数数列 2-a；

子数列 4：a4，a8，a12，…首项为 7-a，公差为 8 的等差数列.

数列{an}的前60项和是子数列1的前15项、子数列2的前15项和的和、子数列3的前15项、子数列4的前15项和的和，从而

角度2：从数列的构成规律来看，着眼于局部.

方法2：前四项从a前的正负来看：

第1项与第3项的和与a无关，第2项与第4项和与a无关；

第5项与第7项的和与a无关，第6项与第8项和与a无关；

第9项与第11项的和与a无关，第10项与第12项和与a无关.

再从上述的和的值来看，第5项与第7项分别和第1项与第3项相同，第9项与第11项分别和第5项与第7 项相同，即有a1+a3=2，a5+a7=2，a9+a11=2.

于是有a1+a3=2，a2+a4=8，a5+a7=2，a6+a8=24，a9+a11=2，a10+a12=40，猜测数列{an}是如下两个子数列构成的：

子数列 1：a1+a3，a5+a7，a9+a11，…是常数数列 2；

子数列 2：a2+a4，a6+a8，a10+a12，…是首项为 8，公差为16的等差数列；

数列{an}的前60项和是子数列1的前15项和与子数列2的前15项和的和，所以

角度3：从数列的项与项数之间的关系上看，着眼于整体.

方法3：由于首项并没有给出，需要设出首项a1=a，在前4项中，第1项，第2项中a前的符号为正，第3项，第4项中a前的符号为负，前4项之和为10，次4项（第5项，第6项，第7项，第8项）的和为26，再4项（第9项，第10项，第11项，第12项）的和为42.

猜测：数列{an}应具有如下性质：

S4，S8-S4，S12-S8，…是首项为 10，公差为 16 的等差数列，S60是此新数列的前15项和，所以

角度4：从数列的构成形式上看，着眼于整体数列一些项的关系.

方法4：从前面分析中不难看出

故可求a2+a3+…+a13的值，又a1=a5=a9=a，估计a13=a1=a，于是利用a1与a13的关系式，就可以研究出a1+a2+…+a12的值.

进一步分析：a3+a2=2×2-1，a5+a4=2×4-1，…，a61+a60=2×60-1，同样的猜测出a61=a9=a，于是有：

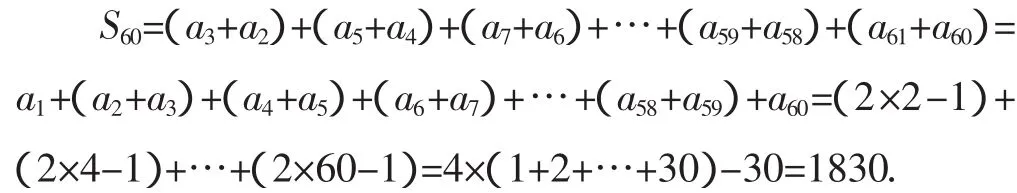
评注：通过观察规律，运用不完全归纳法得出所求结果．

问题2：其结果能否经过严谨推导而求得呢？

任务2 对结果给出严谨的推导.

分析 1：an+an+2=n+1，an+2+an+4=n+3，两式相减得an+4-an=2，

又a1=1，a2=1，a3=1，a4=2，可知：

数列{a4k-3}是以1为首项，2为公差的等差数列；

数列{a4k-2}是以1为首项，2为公差的等差数列；

数列{a4k-1}是以1为首项，2为公差的等差数列；

数列{a4k}是以2为首项，2为公差的等差数列.

从而可知角度1、角度2的计算方法是正确的！

分析2：若将每四项分成一组，则第n组为a4k-3，a4k-2，a4k-1，a4k，设bn=a4n-3+a4n-2+a4n-1+a4n，这样，当n≥2 时，

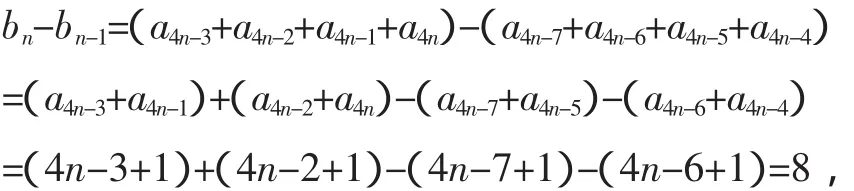
从而可知角度3的计算方法是正确的.

总结：分析1给出了角度1与角度2下构成规律的严格推导；分析2则通过构造出新数列{bn}，证得数列{bn}成等差数列，给出视角3中合理计算的严谨论证.

分析3：证明如下：

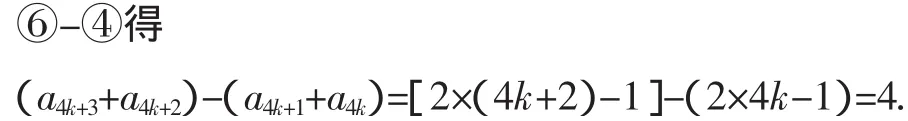
即n≥2 时，（a2n+1+a2n）-（a2n-1+a2n-2）=4，又a3+a2=3，

故数列{a2n+1+a2n}是首项为3，公差为4的等差数列.

由④-③-②+①得a4k+1-a4k-3=0，故a4k+1=a4k-3=a1，故a61=a1，从而可知角度4的计算方法是正确的.

问题3：能否利用前面的方法，求出数列{an}的前n项和为Sn的一般形式呢？

任务3 求出数列{an}的前n项和为Sn.

分析：由上面的经过不难得出：

当n=4k-3 时，an=a，当n=4k-2 时，an=8k-7+a=2n-3+a，

当n=4k-1 时，an=2-a，当n=4k时，an=8k-1-a=2n-1+a，

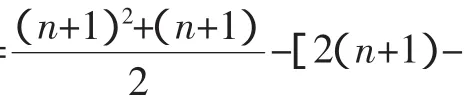
感悟：任务驱动教学法，是指使学生在特定任务的驱动下，借助他人的帮助，利用必需的学习资源，通过问题解决式的自主学习达到教学目标的教学方法.它将传授知识为主的传统教学，转变为以解决问题、完成任务为主的多维互动式的教学.其中的任务，既蕴涵了学生应该掌握的知识、技能和科学方法，也蕴涵了学生应该获得的能力训练和价值观的培养.学生完成任务的过程，是一个不断提出问题、解决问题的过程.这种教学方法的基本特征是以任务为明线，以教学目标为暗线，围绕任务展开学习；教师为主导、学生为主体.

任务驱动教学方法要求师生改变角色，学生起主体作用，教师在教学中起组织、引导作用.这就要求教师通过设计任务、创造情境，激发学生的学习兴趣，调动学生学习的积极性和主动性，使之进行自主探索，同时师生之间互动学习.在完成任务的同时，培养学生创新意识、创新能力以及自主学习的习惯，使学生学会如何去发现问题、思考问题，寻找解决问题的方法.学生的数学学习是积极主动的，使学生带着探究任务进行积极思考、探索，极大地激发学生学习数学的内在动机.

从学习者的角度说，“任务驱动”是一种新的学习法，它把学生的学习活动与任务相结合，使学生的学习目标十分明确.这样学生就拥有学习的主动权，提高了学习效率，获得成功的体验，身心得到发展、激情得到释放，这符合素质教育的要求，是开展素质教育的本质体现.

从教师的角度说，“任务驱动”是一种建立在建构主义教学理论上的教学法.教师把课堂教学目标物化为具体任务，让学生以一个共同的任务为中心，积极主动地应用学习资源，进行自主、合作探究，并通过“任务”链，不断驱动数学探究实践活动，形成学生自主学习的探究态势，从而掌握新知识、提高学习能力的一种教学模式，这种模式改变教师教学观念和教学行为，体现新课程教育的理念.

任务驱动教学法有助于使数学课堂更好地成为学生深入探究问题、互相学习交流的场所，自由表达思想、实现心灵放飞的舞台.一位哲人说过：“学生的思维就像一条不见底的河.”正因为差异，使我们数学课堂教学高潮迭起、精彩纷呈，正因为差异，使我们的数学课堂教学充满了“迷人”的智慧和“成功”的愉悦，要把数学教学过程变成充分展示学生思考、探索、交流、验证的过程，变成关注学生获取知识的过程.新课程标准强调教师要积极地开发、利用“学生”这个教学资源，而这些课程资源就在我们身边，关键是我们要有眼光，善于发现和利用，运用生命学说的理论、动态生成观来优化数学课堂教学，实现师生生命整体价值的整合，做到“我的风采来自于你的风采”；给学生一片探究的时间与空间，学生还我一个精彩的过程与世界.