因图致误问题的再思考
2013-07-25江苏省姜堰市第二中学丁连根
中学数学杂志 2013年15期
☉江苏省姜堰市第二中学 丁连根
一、问题提出
《数学通讯》2012年第6期35页一文《解法大同小异,结果大相径庭》对问题217提供两种解法,但是,结果却不相同,谁是谁非?问题的症结又在何处呢?
二、错因剖析
通过分析,除给出的解法1和解法2之外还可以有第3种解法,我们可以利用解法3来检验解法1和解法2的正确性.

图1
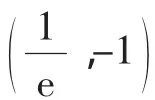


图2

由此可见,问题的症结在于“图形”,解法1是“因图致误”,作图时没有把握住图形的基本特征和关键点,简单处理,想当然地得出答案,错误就在所难免了.
三、解法再探
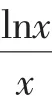

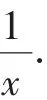
通过求导发现,解法5本质上与解法2是相同的,而解法4中导函数中仍然含有“lnx”,导函数的零点无法直接求出,进一步研究的价值不大.
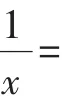



细细算来,这种解法要分8种情况进行讨论,研究这种解法对于提高学生分类讨论的能力,培养解题的意志品质有很好的帮助.
四、解后反思



那么学生在解题时应该如何进行合理的选择呢?我觉得首先要看函数的图像是不是容易画出,而容易画出来的图像又要看交点是否可以方便研究,如果是不熟悉的函数那就要看这个函数的性质是否方便研究,否则解题就解不下去.画图通常要遵循以下的几个步骤:
1.确定定义域,也就是确定函数图像的区域;
2.研究函数的性质:奇偶性、单调性、周期性等;
3.画出关键点和关键线,如渐近线,对称轴等;
4.根据函数的性质画出草图.
