让“美丽的错误”装点出“鲜活的课堂”——一道试题的错误生成与反思应对

☉江苏省徐州市侯集高级中学 陈小祥

数学学习的过程，一定程度上说是一个不断犯错和纠错的过程，学生是课堂的主体，同样也应是纠错的主体，如何利用宝贵的错误资源，抓住学生错误中的合理成分，挖掘错误成因，寻找解决策略，使得解题教学更生动活泼，又效果显然？本文试图从一道高一测试题的讲评案例出发对此做一些探索，不当之处敬请指正.

一、试题讲评实录

有这样一道高一数学测试题（学生已经学过三角函数、基本不等式等内容）：

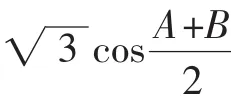
（1）求角C；（2）求△ABC面积的最大值.

教学思路设计：从三种源于学生试卷中的典型错误出发，引导学生去思考、辨析、探究、讨论，找出错因，寻求解法，总结策略，完善认知结构，课前请三位同学在前后黑板上分别板演好典型解题过程.

1.典型错误之不等式应用不到位

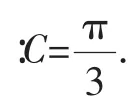
教学主要针对第（2）问，由（1）根据余弦定理可得a2+b2-ab=c2；又a+b+c=12，所以a2+b2-ab=［12-（a+b）］2，化简得

师：请同学们看思路A，其结果是否正确，过程有没有问题，是否严谨？

生1：结果是对的，过程看不出明显问题，我认为是对的.

师：还有没有不同意见？（等待）

师追问：为什么不能这么做，这不是对不等式中取等条件的运用么？

生2：要用不等式求最值，必须考察“正、定、等”这三个条件，这里并无“定”的形式出现，所以用不等式是无意义的.

师：非常好，你能举例进一步说明不能这么做的原因么？（学生思考，教师可启发）

师：非常好，生2举例说明了这样做是不对的，但为什么不对呢？还有其他的解释吗，即为什么不能将取等条件当成新条件代入运算？（视情况可以让学生讨论探究一下，多让学生发言，之后再由教师精讲）

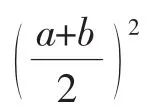
师：非常好，解释得很清楚，有兴趣的同学课后再研究，那么就不能用不等式解了么？

师：很好（停顿一会供学生反思理解），还有应用不等式求解的么？

又 0＜a，b＜12，可解得 0＜a＜6，

令 8-a=t，则t∈（2，8），a=8-t，

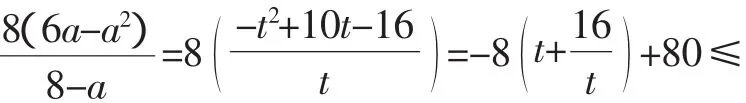
当且仅当t=4，即a=b=4时取等.

师：非常好，你是怎么想的？

生4：要求二元目标式的最值，想到消元思想，结合条件得到其关于a的函数关系式，界定定义域后，根据式子的结构特征，尝试用一次式表示二次式，代换后发现符合使用不等式求最值的条件“正、定”，考察取等号后得到了最值.

师：这里应用的基本不等式求最值与上法中对基本不等式的应用有何区别？

师：很好，通过上面的论述，我们可做如下小结：

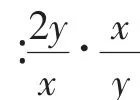
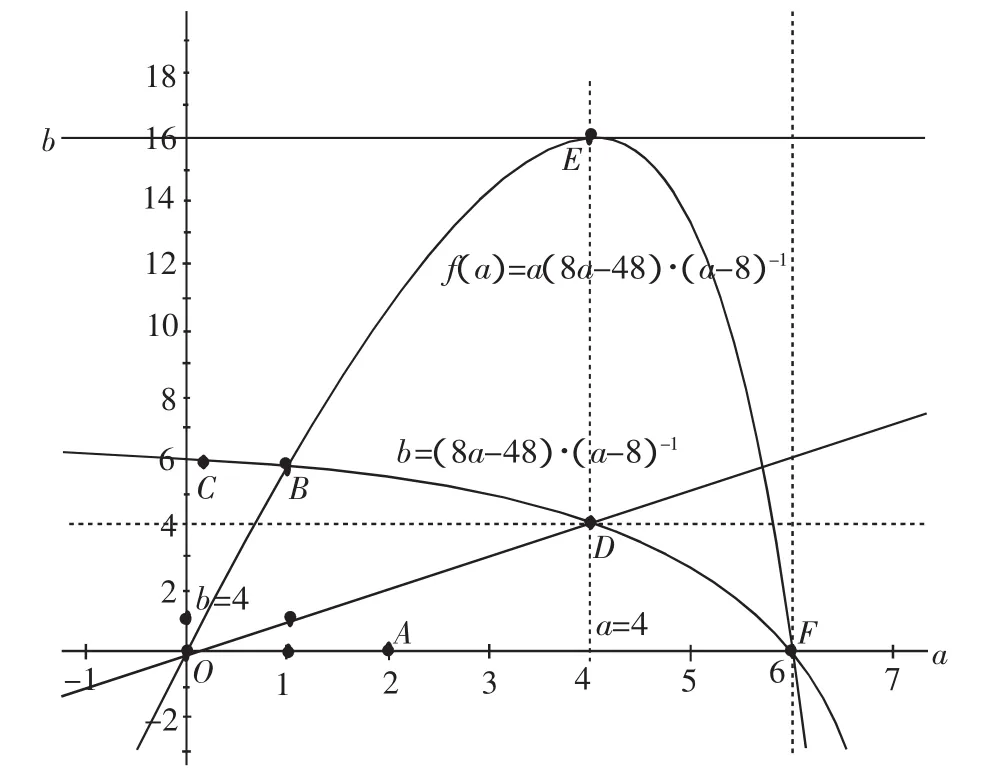
图1

2.典型错误之函数转化不彻底

师：请看，这种解法是否正确，为什么？（学生思考，议论）

师：有道理，那怎么办？能否将R也化成关于∠A的函数呢？

师：很好，利用三角函数中“化异为同”策略，使得式子更简洁，接下来怎么办？

即a=b=c=4.

师：非常好，步步为营，环环相扣，两次运用正弦定理将二元目标式转化为了关于∠A的一元函数式，再根据式子结构，利用诱导公式化繁为简，化异为同，再代换后分离常数进一步简化式子结构，最后结合参数范围和函数单调性求出最值，思路明确，基本功扎实，值得大家学习，此种思路下有没有简单些的方法？

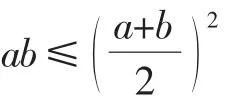
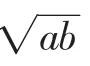
师：真不错，很明显解决过程简化了许多，你能说说这两种解法的联系和区别吗？

生10：两种方法其实都用到了减元思想，都将二元（多元）的目标式转化为单元函数式，都涉及了使用正弦定理进行“边化角“处理，生6的解法其实是结合基本不等式先采用“一次和式”的边角转化求最值后再求原目标式的最值，结构上比“二次积式”的边角转化要简单些，所得式子的最值求解也就简单些.

师：分析得很好（如学生说不到，师再补充），还有要补充的吗？

生7：老师，我是这么想的：

当且仅当a=b=c=4时取等，

师：很好的思路，同学们看有没有问题.

生8：我有疑问，求解中，他将分子abc取到最大值的条件，直接用于求出其外接圆直径，代入比式求得面积值，我觉得这不合理，因为除非分子取最大时分母取到最小，这样比值才最大.

师：嗯，很有道理，那怎么解决呢？

师：非常好的补充，这样原解法才完整，将掌声送给他，谢谢他的精彩阐述（掌声）.

师：很明显这几种方法都涉及了一种常用的求二元目标式最值的方法——目标函数转化法，利用条件将目标是减元后转化为一元函数，再结合具体情况选择方法求最值.

3.典型错误之数形结合不严谨

思路C：如图2.

图2

图3

图4

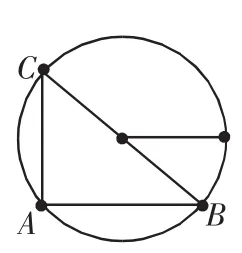
图5

师：你们怎么看这种解法？有无问题？为什么？（留时间给学生思考探讨，一番问答后）

生9：看似正确，但依上面的解法，

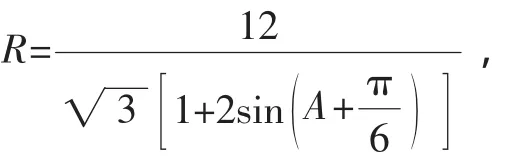
师：非常好，（留学生反思时间）那怎么办呢？

生9：看来数形结合解不出来，那只能回到前面的解法中去.

师：那我们退一步，你能改变条件使得可以使用类似的几何法吗？

师：很及时的变化，非常棒，从上面的不同错误及其辨析过程以及多种解法的角度我们可以总结一下二元（多元）目标式最值求法的一般策略：不等式（基本不等式及变式、柯西不等式等）、线性规划及相关知识、一元函数转化等方法是高中多元函数式最值问题求解的常用策略，大体上可分为数与形两类，从数的角度看多将多元目标式划归为一元函数式，或者利用不等式直接求最值；从形的角度则多从条件出发寻求目标式或其变形式的几何意义如：为面积、距离、斜率等或划归为线性规划问题求解，更多的时候往往综合灵活运用以上策略以顺利求解.下面请同学们整理反思这些解法，并完成下列相关练习：

（1）已知x>0，y>0，x+2y+2xy=8，则x+2y的最小值为______；xy最大值为______.

（2）已知x>0，y>0，4x2+y2+xy=1，则 2x+y的最大值为______；xy最大值为______.

（3）已知x>0，y>0，2x+8y-xy=0，则x+y的范围是_____.

二、常用的错误应对策略

①充分预设，以误引辩，辩在重点难点处.教师需充分筛选研究典型的、普遍的、有价值的错误，在课堂上通过各种方式引导学生于重难点处辩论，注意调控辨析走向，务必保证找准问题，辨清矛盾，得到确解.不同想法的碰撞不仅能凸显问题的内在价值，而且会使得学生的知识和能力在辨析中内化和提升；

②动态生成，示误引思，加深知识方法理解.教学应该是预设与生成的统一，生成才是课堂迷人的地方，因为总会有出乎你意料的想法出现，而当学生探究、评论有误时，教师可以将其看成新的资源，继续诱其深入，引其自纠，培养求异思维.如有必要还可继续通过一题多解等形式将学生思维引领至更高的层次，引导学生纠正反思错误，进而总结知识方法，以加深理解；

③变式教学，纠错巩固，促进认知结构完善.通过适当的一题多解、一题多变与多题一解的题组教学与练习让学生体会到变和不变之间的联系，加深学生对各种解法及相关知识的深入理解，从而构建更完善的认知结构；

④二次练习，强化认识，防止错误反复.一周内再次给出关于典型错误的二次练习非常必要也非常有效，视情况再进行教学设计乃至三次练习，适度的重复练习对应试必要而有效.

综上，教师应积极面对学生的错误，认真收集、整理、筛选有价值的错误资源，选择合适的时机和方式，引导学生去辨析、思考、交流、探究、纠错、拓展和反思，让学生的思维在解题教学课上动起来、活起来，进而促进新的认知结构的完善和解题能力的提高.

1.张爱珠.浅谈高中学生数学思维障碍及对策［J］.福建教育学院学报，2006（6）.

2.黄彩祥.高中数学解题心理性错误分析［J］.河北理科教学研究，2003（3）.

3.吴卫东.开启从错误中学习的新视角［J］.新课程周刊，2009（3）.