创设概率背景 凸显命题立意

☉江苏省滨海中学 徐君华

浏览近年来高考试卷，不难发现概率统计题也融入新课标的教育理念，多角度、多视点地考查学生的数学素养，使学生的自主性和个性得以发挥，体现数学与社会、人与自然的和谐统一.许多试题体现了时代气息，有创新特色.下面以2013年部分省市概率考题为例简析如下.

一、关注热点，联系实际，极富时代气息

例1 （2013年北京理）如图1是某市3月1日至14日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染，某人随机选择3月1日至3月13日中的某一天到达该市，并停留2天.

图1

（1）求此人到达当日空气重度污染的概率；

（2）设X是此人停留期间空气质量优良的天数，求X的分布列与数学期望；

（3）由图判断从哪天开始连续三天的空气质量指数方差最大？（结论不要求证明）

解析：设Ai表示事件“此人于3月i日到达该市”（i=1，2，…，13）.

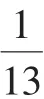
（2）由题意可知，X的所有可能值为 0，1，2，则

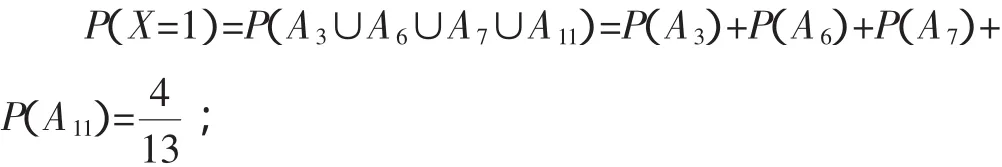
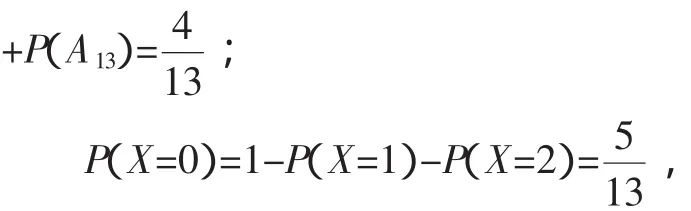
所以X的分布列为

images/BZ_299_1402_1115_2187_1294.png

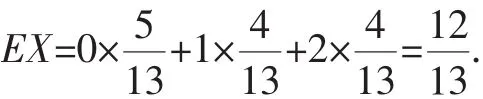
（3）从3月5日开始连续三天的空气质量指数方差最大.

评析：该题直接关注当下的热门“空气质量”问题，引起了很多老师和学生的兴趣，让考生感到数学试题有了贴近生活的一面.它旨在教会学生学以致用，把知识运用到生活中.

二、代数几何，交汇融合，命题立意深远

近几年的高考概率试题呈现出综合性，如“概率与函数、不等式”、“概率与数列”、“概率与方程”、“概率与线性规划”等相结合的应用题，也出现了与横向学科相联系的问题，体现了新课程的教育理念.

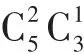
评析：本题以方程为依托，以排列组合和概率知识为工具，考查双曲线的性质和分类讨论思想，同时也对集合中的元素的分类进行了考查.

三、联系生活，多向发散，意在创新能力

（1）若小明选择方案甲抽奖，小红选择方案乙抽奖，记他们的累计得分为X，求X≤3的概率；

（2）若小明、小红两人都选择方案甲或方案乙进行抽奖，问：他们选择何种方案抽奖，累计的得分的数学期望较大？

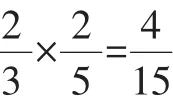
（Ⅱ）设小明、小红都选择方案甲抽奖中奖的次数为X1，都选择方案乙抽奖中奖的次数为X2，则这两人选择方案甲抽奖累计得分的数学期望为E（2X1），选择方案乙抽奖累计得分的数学期望为E（3X2）.

因为E（2X1）＞E（3X2），所以他们都在选择方案甲进行抽奖时，累计得分的数学期望最大.

评析：本题是比较大小型试题，考查不放回的抽球、重点考查等可能事件、对立事件的概率，在知识应用上有一定的灵活性.

四、立足根本，回归教材，展现命题理念

例4 （2013年湖北理）如图2，将一个各面都涂了油漆的正方体，切割为125个同样大小的小正方体，经过搅拌后，从中随机取一个小正方体，记它的涂漆的面数为X，则X的均值E（）X=（ ）.

图2

解析：X的可能取值为 0，1，2，3，分为以下情况：

当X=0 时，可看作切除“5×5×5正方体”的表面，得到一个“3×3×3 正方体”，故n（X=0）=3×3×3=27；当X=1时，一面涂色小正方体位于每个面的面心呈“3×3”分布，故n（X=1）=3×3×6=54；

当X=2时，两面涂色小正方体位于每条棱上呈“3×1”分布，故n（X=2）=3×1×12=36；

当X=3时，两面涂色小正方体位于每个顶点上呈“1×1”分布，故n（X=3）=1×1×8=8.

X的分布列为：

images/BZ_300_1397_1684_2298_1862.png

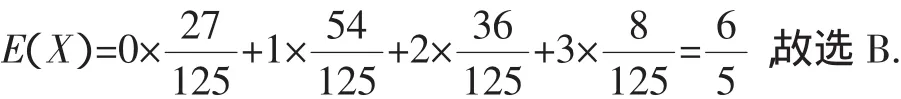
评析：本题源自人教A版必修2第36页A组题9：一个红色的棱长是4 cm的立方体，将其适当分割成棱长为1 cm小正方体，问：

（1）共得到多少个棱长为1 cm的小正方体？

（2）三面涂色的小正方体有多少个？表面积之和为多少？

（3）二面涂色的小正方体有多少个？表面积之和为多少？

（4）一面涂色的小正方体有多少个？表面积之和为多少？

（5）六个面都没有涂色的小正方体有多少个？表面积之和为多少？

试题源于课本，高于课本.综合考查了空间几何体、古典概型和离散型随机变量的分布列等知识，很好地整合了代数与几何的交汇融合，立意深远，有一定的区分度，属中等难度题.

总之，近年来，以离散型随机变量为平台，以实际应用为背景，已经成为高考的热点问题.这样既能考查概率统计的核心内容和方法，又能考查综合运用所学知识分析问题和解决问题的能力.