课标引领教材落定——基于2011年版修订课标之初中教材首章《有理数》的探变<br/>

课标引领教材落定——基于2011年版修订课标之初中教材首章《有理数》的探变

2013-07-25山东省滨州市北镇中学初中部邢成云

中学数学杂志 2013年8期

☉山东省滨州市北镇中学初中部邢成云

作为初中阶段教材的开篇《有理数》，其变与不变自然有着对初中阶段数学教材的统领作用，2011年版课程标准修订版的出台，引领了教材的修订，2012年秋季教材的面世，给了我们进一步理解课标的机会.本文拟以《有理数》一章为例，探寻新教材的变化，意欲以绵薄之力服务于教材的建设，进而指导自己的日常教学.

一、导入环节之变

除了减掉“有效数字”这一2011年版课标明文提出的概念外，本章的主体内容变化微乎其微，但有部分节次的导入环节却有变化.仔细研读、对比，不难发现变化的目的是为了更好地突出数学本味儿，淡化生活味儿，消除了某些无谓的干扰，降低了外部认知负荷，便于学生更好地感知数学、理解数学.

如有理数乘法的开篇，舍弃了原来烦琐的实际问题，通过相对简约的形式，从探寻规律中合情入理地引入课题，突出了思想性，发挥了类比的引领作用，把学生从烦琐的实际问题的漩涡中拉了出来.

又如有理数的乘方的导入环节，较之原实验版拉长了概念的形成过程，从明确研究乘数相同的运算开始，遵循从特殊到一般的认知轨道，步步深入，揭示课题.

二、例题之变

例题是有导向作用的，无疑，它的变化是对2011年版课标变化的顺应.如第18页的例2，顺应了前文中有关净胜球的引例的舍弃，减少了外部干扰，有助于学生对数学本质的理解.

另有部分例题的内容变得充盈丰满，从类型上变得全面，从梯度上变得有层次感，并非原来的突兀呈现.

如新教材第30页的例1，原实验版第30页如此设计：

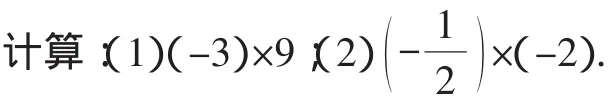
现在的修订版改为：

可见，变原来的2个小题为3个，不但丰富了题目的内涵，使得原有的两种类型“负乘正”“负乘负”成为“负乘正”“正乘负”“负乘负”三种形态，而且通过增补第二小题及其旁注，渗透了从运算的角度确定一个数的相反数的方法（对相反数概念的别样解读）.

再如第45页的例5，原实验版第45页如此设计：

用科学记数法表示下列各数：1000000，57000000，123000000000.

现在的修订版改为：

用科学记数法表示下列各数：1000000，57000000，-123000000000.

虽然仅是其中之一一个符号的变化，但价值定位存在落差，由原来一味地表达一类数——正数，变成了两类数，使得科学记数法的应用范围全面展现，避开了单一形式形成的误导嫌疑，可谓一个符号改变了境界.

三、题目之变

此处的题目专指教材中的练习、习题和复习题.修订版教材对原实验版题目进行了适当的增补、删减、调整，使每个题目能更好地发挥“各司其职、各尽其能”的应有之力.

1.调整顺序

次序的变化，愈加贴近学生的实际，符合由易到难、由具体到抽象，梯度渐进的基本规律，针对性更强.

如1.1《正数与负数》的两组小练习，前后整体互换，顺应了教材的顺序调整，并在第一组练习中增加第二小题，突出了相反意义的量，具有承上启下之作用，整体而言，符合从实际问题到数学问题的过渡.而原教材恰好相反，使得思维倒置，有悖于学生的认识序列.

再如1.2.2《数轴》一节的练习，把原来的1、2两题对换，变原来的“画数轴——表示数——读数轴写数”为现在的“读数轴写数——画出数轴——表示数”.如此，理顺了由易到难的脉络，因为读数轴写数远比画数轴表示数简单得多.

总之，题目调整后的顺序，更符合从易到难、从简单到复杂的逻辑联系和思维要求.

2.充盈内容

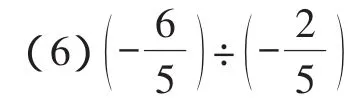
又如复习题1增设的第11题和第16题，一个以实际问题为背景，综合了数的有关运算，能让学生在解决问题的过程中领悟数学的价值，一个以计算器为媒介，着眼于学生的合情推理，重在渗透发现问题、提出问题的问题意识.

3.增补题目

（1）增加练习.

如第19页的练习增设第4题，该题是一道链接生活但不失数学味儿的题目，是对同一数学式子作出多样化理解的渗透，是关注学生个性差异的体现.

再如第45页的练习增设第3题，该题是一道链接生活的跨学科题目，是学以致用的一种体现.

（2）增加习题.

如第14页的习题1.2复习巩固栏目增设第4题，它是对相反数概念的巩固，同时渗透了数形结合思想.

（3）增加复习题.

修订版复习题1第51页的第7题、第8题均是新增题目，其中第7题顺接了前文第45页例5及练习1、第47页习题1.5的复习巩固5合众托出的科学记数法；第8题虽然运算难度较小，但融入了绝对值，并有意让学生比较--3与-（-3）的异同，引领学生形成深度审视题目的好习惯.

4.删繁减难

有关净胜球的题目全部删去，因为原有的净胜球的引例和相关例题均被删去，“净胜球”一词专业性较强，干扰了学生对数学的认识，修订版将其割舍是合理的.如原实验版第26页的第11题、复习题1第51页的第7题等.

四、思想方法得以加强

本次修订版教材的一个突出特点就是把数学思想方法摆在了“桌面”上，使其显性化了.在本章的小结中，数形结合、转化的思想方法被明确提出，这种表述的显性化，突出了新添“一基”——基本思想方法的地位，这是原实验版教材所没有的.

另外，在本章的题目设置上，也加强了对数学思想方法的植入，增添了4道题目凝聚于“数形结合”的渗透，如第9页的练习3，强化位置与数的对应，帮助学生借助数轴认识正数、负数；第14页的第3题复习巩固，借助数轴工具在平移中感知数，并为后续有理数的加法法则的探索做了伏笔；第15页的第10题体现综合运用，以数轴为载体，在分清距离大小与数轴上的点所表示的数外，还为以后学习对称，尤其是二次函数的对称做了铺垫；第52页复习题1的第10题体现综合运用，把数形结合提到一个较高的境界，灵活考查了学生对这一思想的认识，通过数轴展现信息，由形到数，然后回归数轴，帮助学生认识到相反数在数轴上的相对位置，由数到形，结果会一目了然，数形结合相得益彰的魅力可见一斑.无独有偶，在增加的内容中也有体现：如第24页的探究等.

同时，在新加题目或内容片段中渗透分类思想也较为突出，如：

1.2.1增加一个练习，即第7页的练习2：指出下列各数中的正数、负数、整数、分数：

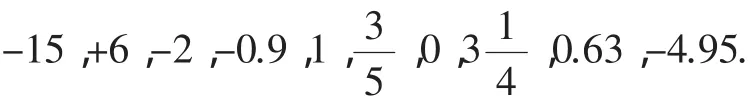
1.3.1《有理数的加法》第16页的第1个思考：小学学过的加法是正数与正数相加、正数与0相加，引入负数后，加法有哪几种情况？

教材思想方法性的增强，从物化的题目加强中可见其踪影.

五、关注与小学阶段的联系

关注与小学阶段的衔接，基于学生的认识基础和已有经验，很多地方明文提出“在小学，…”等字样，而原实验版一般使用含糊其辞的说法“我们已经…”，似乎与小学处于断层状态.

比如在章引言中的论述颇有差异：原实验版教材如是说：“通过本章的学习，你将认识一种新的数——负数”；而修订版教材则说：“本章我们将在小学认识负数的基础上，…”.实际上，小学5年级就已经开始接触负数了，原来的说法委实不妥.

另如，第34页增加了一句“与小学学过的除法一样，…”打通了小学与初中的阻隔，顺利实现了迁移，符合学生的认识心理.

再如，第36页增加了一句“与小学所学的混合运算一样”，再次让学生感受到小学与初中的自然衔接.

可见，增添的语句或许是只言片语，但有效联通了小学、初中，让学生能感觉到初中无非就是小学已学知识的发展，并非另起锅灶，消除了神秘之感，有利于学生对“四基”的把握与领会.

六、思考栏目变多，问题意识增强

学会思考、学会思维是数学的核心任务，通过栏目的变化，督促学生质疑善思，培养问题意识，打造智慧大脑.

如1.2.3《相反数》一节，在给出相反数的概念，并通过实例分析后，增设“思考”环节：设a表示一个数，-a一定是负数吗？

笔者认为这个问题设置的好，把学生心中的困惑“揪”了出来，给学生以思维碰撞的机会，从而加深其认识.教材如此设置，抓住了学生的思维困惑点，可谓恰到好处.

另外，有部分“云图”也为凸显问题助阵，如1.5.1《乘方》一节中，第41页的“云图”“（-2）4与-24一样吗？为什么？”，把学生心中的纠结搬出来供思考，通过异同点的分析，能加深对底数、指数的理解.

第24页增加了一个探究活动，能引起学生的深度思考，它意在引导学生探索出数轴上任意两点之间的距离公式，关于这类问题，前面已有多处铺垫，置于此可谓水到渠成.

七、加大了运算力度

新的关键词“运算能力”在课标修订版中的提出，导航了教材的编写，从题目的变化中折射出加大运算力度的信号.

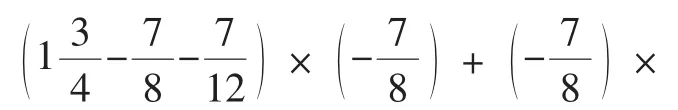
八、更加突出过程

过程、结果相携而生，知识的来龙去脉才会明朗，才会深入人心，从而成为学生智慧的永恒元素.

1.练习设置垫脚题

如“有理数的加法”一节增加的练习：

第18页练习2：口算：

（1）（-4）+（-6）；（2）4+（-6）；（3）（-4）+6；

（4）（-4）+4；（5）（-4）+14；（6）（-14）+4；

（7）6+（-6）；（8）0+（-6）.

可见，题目虽然简单，但除不含正数加正数的题目外，其他组合全都有，可以说全方位地反映了加法法则，这种通过口算过渡的方式非常可取.

如“有理数的乘法”一节增加的练习：

第32页练习1：口算：

（1）（-2）×3×4×（-1）；

（2）（-5）×（-3）×4×（-2）；

（3）（-2）×（-2）×（-2）×（-2）；

（4）（-3）×（-3）×（-3）×（-3）.

原来的4个计算都相对复杂，有多个因数且夹杂着符号的干扰，直接让学生运算颇有阻力，为此设置了练习1，借助口算，首先帮助学生把符号搞定，一是服务于紧接的练习2，同时也为后续有理数的乘方概念及运算性质的得出做了铺垫，可谓一石二鸟.

如“乘方的意义”一节增加的练习：

第42页练习1：（1）（-7）8中，底数、指数各是什么？（2）（-10）8中，-10叫做什么数？8叫做什么数？（-10）8是正数还是负数？

不难看出，这一练习直指底数、指数的概念，从正反两个方面帮助学生认识，给执教者做了价值引领.

2.减缓坡度、分解过程

1.2.2《数轴》的学习，原教材是一个引例图示加一个温度计模型定“乾坤”，而修订版教材把原引例图示分解为三个阶段，成为三个图，对应着三次抽象，一个是实际意义图示，它借助的是生活经验，第二个图示是在第一个的基础上抽象而来的，尚不完备，第三个图才规范呈现，如此设置，实现了实际问题——数学模型——数轴模型的渐次抽象，符合刚刚从小学进入初中的学生的认知心理，这种拉长有助于学生对数轴的领会.

九、小结之变

小结共分两部分，其中第一部分“本章知识结构图”没有任何变化，但第二部分“回顾与思考”进行了较大调整，是修订版教材变动较大的地方之一.它在原来6个直白问题的基础上，首先对负数引入的意义做了阐明，接着从整数与分数统一性的角度，明确了有理数的概念（内涵与外延），然后以有理数的运算为载体，对其间彰显出的数形结合、转化等数学思想、方法做了明确的揭示，归纳出算律、算法，最后对原来的问题稍作调整，给出了5个问题供复习思考（原来的问题6调整到内容的梳理中），使5个问题更具有“引桥”作用.

这种宏观的梳理，贯通了前后，起到了画龙点睛的作用，笔者认为如此修改，使得小结更具有统摄性、思想性，更有利于学生的回顾、思考、复习.