分类讨论思想在解题教学中的实践和思考

☉江苏省南通市通州区育才中学 黄新颜

数学思想方法是中学数学教学的最高境界，用华罗庚大师的话说：教师首先教学生的是数学的双基知识，这只不过是数学的分散知识点，好像一维的数轴；其次教师应该指导学生进行知识点之间的联系，也就是现在中考常常出现的知识点交汇处的考查，好像是二维的坐标系一般；最后教师应带领学生走进数学思想方法的殿堂，这里才是数学最漂亮、最完美的地方，犹如是一个变换般的三维空间.因此，中学数学教学的核心是数学思想方法的教学.

众所周知，分类讨论思想是初中数学的重要思想方法，在解决很多初中数学问题时有着不可替代的作用.其早在中国古代刘徽等人的专著《九章算术》中就已经被多次使用，如今更是在中考数学中层出不穷，成为区分学生思想完整性、发散性、灵活性、严谨性等的必备数学思想，值得教师研究和深化.

一、在函数问题中的运用

例1 （苏州2012年中考模拟）如图1，已知A、B是线段MN上的两点，MN=4，MA=1，MB＞1. 以A为中心顺时针旋转点M，以B为中心逆时针旋转点N，使M、N两点重合成一点C，构成△ABC，设AB=x.

（1）求x的取值范围；

（2）若△ABC为直角三角形，求x的值；

（3）探究△ABC的最大面积.

分析：点B在AN上运动，通过观察可得∠CAB和∠ACB可以成为直角，∠CBA不可能成为直角.

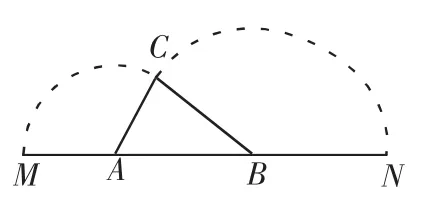
图1

（1）根据三角形的基本性质：两边之和大于第三边以及两边之差小于第三边，找寻关于x的不等式，进而得出x的取值范围；

（2）对Rt△ABC进行分析，由勾股定理进行分类，讨论存在性；

（3）把△ABC的面积S的问题，转化为S2的问题，AB边上的高CD要根据位置关系分类讨论，分CD在三角形内部和外部两种情况.

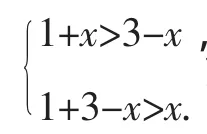
（2）①若AC为斜边，则1=x2+（3-x）2，即x2-3x+4=0，此方程无实根；

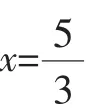
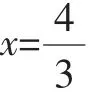
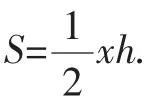
①如图2，若点D在线段AB上，则=x，得平方得 （3－x）2－h2=x2－2x，得，平方得x（21－h2）=9x2－24x+16.整理，得x2h2=－8x2+24x－16，所以

②如图3，若点D在线段MA上，则

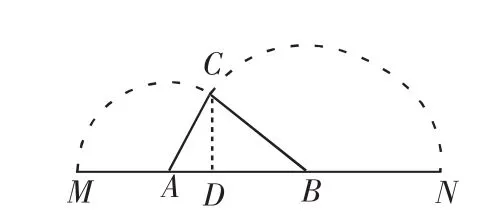
图2

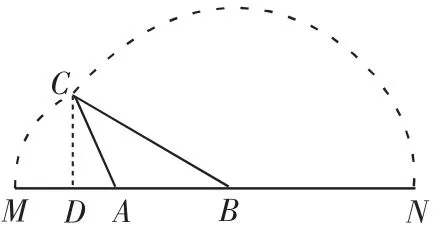
图3

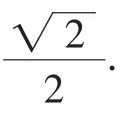
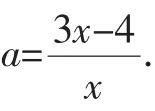
二、在应用题型中的运用

例2（2011年南京中考）学生甲和乙分别站在一边长为10的正方形ABCD的点A和点D处，现在甲从点A出发，设其在正方形边界上沿着逆时针匀速运动（如图4），速度为每秒2个单位（位置记为点P），求学生甲（点P）和学生乙（点D）之间的距离.

分析：学生甲从点A出发，到达B、C、D、A的时间分别是5秒、10秒、15秒、20秒，显然对问题的分析要以时间的临界状态为分类讨论的切入点，因此：

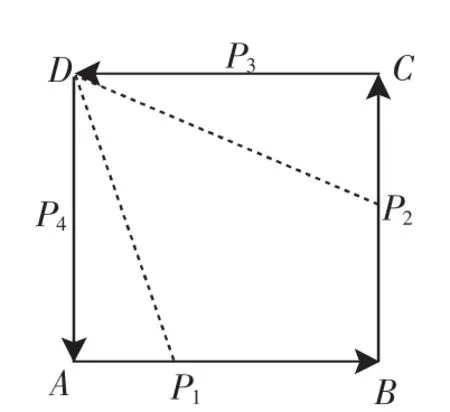
图4

（1）当0≤t＜5时，学生甲的位置P落在线段AB上，此时

（2）当5≤t＜10时，位置P在线段BC上，此时PD=

（3）当10≤t＜15时，学生甲的位置P落在线段CD上，此时

（4）当15≤t≤20时，学生甲的位置P落在线段DA上，此时

综上可知：学生甲（点P）和学生乙（点D）之间的距离可用一个分段函数表示，下略.

提示：本题在实际应用型问题的背景下，体现了问题的运动观点 （也是函数思想在实际应用型问题中的体现），考查了学生甲（点P）和学生乙（点D）之间的距离，应根据点P的不同位置分析不同情形，而分类讨论的关键切入点在于正方形每个转折处.

三、在方程中的运用

例3 求使关于x的方程kx2+（k+1）x+（k－1）=0的根都是整数的所有k值.

分析：本题中并未说明方程一定是二次方程，所以首先要对k是否等于0进行分类.当k=0时，显然所给方程为一次方程，有整数根x=1；当k≠0时，可以设两个整数根为x1、x2，由韦达定理可知：

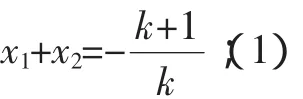
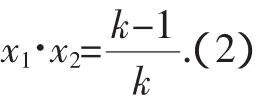
（1）－（2）得：x1+x2－x1x2=－2，有：（x1－1）（x2－1）=3=1·3，因此：

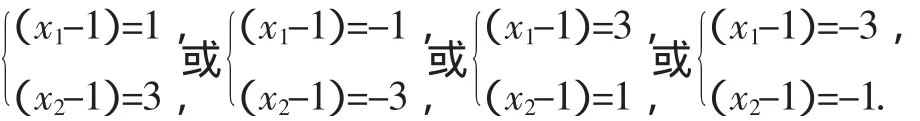
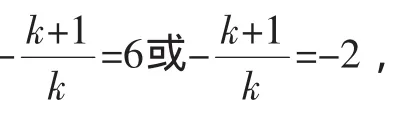
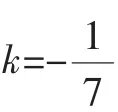
提示：对于方程问题，首先不要将思维定势在二次方程中，教师只有引导学生抓住了分类讨论的动因，把握住了分类的标准，才能做到分类时条理清楚、标准一致，在解答问题时就不会重复或遗漏，才能保证解题的准确率.

四、数学思想教学的思考

初中数学有很多的基本知识，我们称之为双基知识，这是学生必须掌握的一维知识点；其次初中数学知识点板块之间的综合运用，称之为知识交汇处，需要教师通过一定指导，使学生通过训练达到，即所谓学生的二维知识链；初中数学学习的最高境界是掌握数学思想方法，即所谓的三维知识模块，将千变万化的试题化有形于无形中，通过思想方法看到问题的本质、解决的思路，这是每个优秀学生学习的最终目标.熟练掌握初中数学思想方法对每个学生来说并不容易，因为这首先需要一维知识点和二维知识链的熟练掌握，其次才是运用这些思想——为了将我们遇到的问题进行解决或转化.众所周知，学生学习数学思想方法有一个循序渐进的过程，首先应学会数学的双基知识，其次对知识进行整合获得知识间的联系，最终才是用数学思想方法进行提炼，将其牢固的粘合于学生的知识体系中.通过上述案例，笔者认识到分类讨论思想在教学中的重要性，更能从分类讨论思想中管窥中学数学教学中思想方法教学的重要性.

（1）掌握数学思想方法是学习数学知识的本质，数学思想方法渗透于数学的各个分支，是我们解决数学问题的重要导向，是探究性学习的重要工具之一.把掌握数学方法和思想作为数学教育的重点，可以使初中学生逐步掌握数学基本方法和数学思维，进而展开高效率的数学学习.数学方法和思想是初中学生提高数学素养、培养创新能力的关键，是一切数学创新的源泉，数学思想方法的教育使数学教学真正变为“授之以渔而非授之以鱼”，让初中学生由“学会”变成“会学”，为其今后终生学习奠定基础.

（2）数学思想方法的教学使学生更容易理解数学科的内容，使其在掌握了一些数学思想方法后再去看待相关的数学知识显得“高屋建瓴”.挖掘初中更深层次的问题，这样的学习更具稳定性，有利于旧知识的巩固和新知识的学习，能够顺利将新知纳入到自身知识体系中去，数学思想方法正是体现了这么一种核心.

近年来，对初中数学思想方法的考查越来越受到各地中考的重视，教师在教学中也要从初一的教学开始就全面渗透对数学思想方法的学习，提升学生通过问题看本质的能力，使其在掌握扎实的双基的同时，将知识点进行有机的整合，最终上升到思想方法的高度进行提炼，久而久之，就可以提升优秀学生的数学能力和数学素养，用诺贝尔奖获得者李政道教授的话说：“我觉得今天取得的一点成就离不开数学的功底，而数学的功底又在于我当年中学时代对数学思想方法的理解和运用，其伴随我研究一生.”

总之，数学思想方法是研究数学中发现、发明、创新和其他创造性思维活动的规律和方法，以及探索数学发展的一门科学.数学已经渗透到各个领域，并成为其思想和行动的指南，数学思想方法是一种思维，一种思考问题的方法模式，它体现了辩证法的原理，它不仅用于解决数学问题，更可以应用在人们日常的事务处理、问题思考中.

1.徐利治.数学方法论选讲［M］.武汉：华中理工大学出版社，2000.

2.波利亚.数学与猜想［M］.北京：科学出版社，1984.

3.臧雷.“数学思想方法研究综述”［J］.中学数学教学参考，2002（10）.

4.刘晓玫.论数学思想方法在数学教育中的作用［J］.首都师范大学学报，2001（10）.