寓新课序幕于问题情境中

☉天津市静海县沿庄镇中学 刘家良

在数学课堂中，部分教师为了能让学生在45分钟内尽可能多地获取知识，多做几个题，常常忽视乃至略去新课导入情境环节的教学，误认为导入情境教学会白白耽误学生的时间，没有实用性.这种将缺乏情境化的知识直白地灌输给学生，虽然学生知识增多，成绩暂时高些，但是数学兴趣却伴随着知识量增长的同时越发受到压抑，因为学习不是一种发自内心的愉悦需求，而是一种外部力量（考高分升学）的强加.如此下去将会直接导致“三维目标”中情感目标的缺失，致使学生的发展出现畸形，将有损学生的身心健康.

问题是数学的心脏，有了问题，思维自然就有了起点和方向.问题源于情境.问题情境能有效地解决知识的抽象性和学生思维的具体性二者之间的矛盾.创设一个适宜学生“最近发展区”的问题为课堂教学的导入情境，是激活课堂教学气氛的起点，是激发学生探究新知兴趣的源泉.精彩的导入是课堂教学成功的一半.那么，在新课伊始，教师创设什么样的问题情境，能诱发学生发现问题和提出问题，使学生带着悬念在内心深处产生一种迫切的求知心态，从而进入有效的学习状态之中呢？

一、寓新课序幕于生活化的问题情境中

以生活中的实际问题为背景，做为新课导入的素材呈现给学生，让学生设法去解决.由于学生心里怀有一种解决问题的念头，就会揣着问题去听课，学习自然就会产生一种驱动力.以生活化的问题情境为导入拉开新课序幕，会使学生感觉所接触到的知识不是从空而降，而是来源于身边的生活，是看得见，摸得着的.反过来所学知识服务于生活，又体验到这样的学习是有用的.因此，它不仅能极大地激发学生学习数学知识的兴趣，而且能增强学生自觉应用数学知识解决问题的意识.以生活中的素材为问题情境，不是一种目的，而是要通过这种“生活”的启发抽象出数学模型.

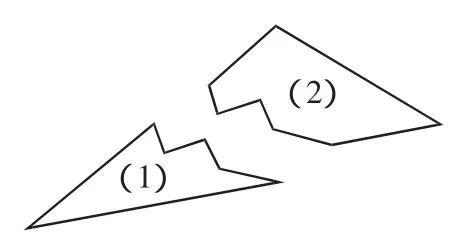
图1

案例1 如图1，小明不慎将一块三角形模具打碎为两块，他是否可以只带其中的一块碎片到商店去，就能配一块与原来一样的三角形模具呢？如果可以，带哪块去合适？

分析：问题的实质就是看这两块碎玻璃片中哪一块能够还原成原始的三角形.其中玻璃片（1）只具备原始三角形的一个角，而由前面的学习得知当两个三角形具备一角相等时不会全等，而玻璃片（2）具备原三角形的两个角及其夹边，并且能还原到原始的三角形.玻璃片（2）留下三个已知元素，学生自然就会发问：两个三角形具备“角边角”的条件时，是否会全等呢？由此拉开全等三角形“角边角”判定法的序幕.

案例2 如图2，△ABC是等腰三角形，AB=AC.倘若它的一部分被墨水涂没了，只留下一条底边BC和一个底角∠C，请同学们想一想，有没有办法把原来的等腰三角形重新画出来？

分析：由已学等腰三角形的性质可知：若AB=AC，则∠B=∠C.此时学生自然会逆向思考：若∠B=∠C，是否会有AB=AC呢？由此拉开“等腰三角形判定”的序幕.

以上两个问题皆源于生活，这种生活化的问题情境的创设，能吊起学生的胃口，激发学生主动参与课堂探究的积极性.

值得注意的是：“生活化”问题情境的创设需建立在学生熟悉的生活经验和已有知识经验的基础上，引导学生寻找到欲解决的问题和要学知识的“契合处”，明确问题中蕴含的数学问题，为学生经历概念的形成及定理的探究指明方向.

图2

二、寓新课序幕于游戏式的问题情境中

初中生有着强烈的好奇心和旺盛的求知欲，不管什么事情总想刨根问底，好弄个究竟.然而，数学教学中有相当一部分内容学起来枯燥，教起来干瘪.教师若能将这些内容经过加工改造后再以游戏方式呈现在学生面前，学生就会感觉到这些知识自然、生动、有趣，学生回答起问题来也会争先恐后，从而改善学生学的被动状态.游戏式的问题情境就是先由老师提出任务要求，让学生围绕这一任务给老师出题，和老师“挑战”，所谓的“刁难”老师.而老师对问题的结果却能脱口而出，因出乎学生的意料，学生感觉惊讶，为尽快弄清“谜团”，就恨不得学会老师的“绝招”，由此拉开新课的序幕.

案例3“一元二次方程根与系数的关系”一节的序幕拉开，笔者就采用了上述方式.首先，让同桌的同学相互给对方出一道一元二次方程求根题，之后笔者说：“请你把两根告诉老师，老师就能立刻猜出你解的那个一元二次方程，谁能试一试？”这时，有几个学生拿出自己的两根和老师“挑战”，结果笔者都能说出他们所解的一元二次方程，此时，学生兴趣盎然，但又感惊讶，老师这么快得说出，一定有什么“高招”吧.这时，有的学生猜测：既然知道两根，能求作一元二次方程，那么，方程的两根与方程的系数是否存在某种联系呢？学生因为有了“迷团”，思维自然兴奋起来，就会去揭开问题的神秘面纱.由此拉开了“根与系数的关系”的探究序幕.

游戏式的导课方式，会使学生学得生动一些、主动一些.但游戏式的问题情境常会打乱课堂“章法”，所以老师设计游戏时，一定要紧紧围绕教学展开，有明确的目的、规则和程序.

三、寓新课序幕于操作式的问题情境中

教育家陶行知先生说：“人生两个宝，双手和大脑.”动手操作是一个手脑并用的过程，是获取感性认识的主要途径，是学生学习过程中的创造性思维活动.然而，传统数学教学过分强调智能逻辑思维的训练，而缺乏动手操作能力的培养，致使长期以来学生动手能力差.为改变这种现状，教师应尽量为学生创设动手操作的条件和机会，使学生在动手操作中对数学概念、定理等获取感性认识，接着，通过加工、整理上升为理性认识.对教材中某些几何图形的性质、判定，教师若能引导学生通过折、量、画、拼、剪等活动来拉开新课序幕，则不仅能使学生积累数学活动经验，而且能使学生逐步养成勤于动手、主动观察和善于发现的良好学习习惯.

案例4“等腰三角形的性质”一节就是先从一张长方形纸片对折后的图形中剪下一个重叠的直角三角形，将其打开，在获得等腰三角形的动手中拉开新课序幕的，然后在教师引导下，通过学生自己观察、发现和归纳等系列活动去获取等腰三角形的性质.

案例5 如图3，用一根木棒和一根弹性均匀的橡皮筋，做一个简易的“弓”，“箭”通过木棒中央的孔射出去，怎么才能保持射出箭的方向与木棒垂直呢？为什么？

1.活动：通过图形将上述问题进行转化.作线段AB，取其中点P，过P作直线l，在l上取点P1、P2，连接AP1、AP2、BP1、BP2.此时有两种可能：其一，如图4，AP1≠BP1，直线l与AB不垂直；其二，如图5，AP1=BP1，直线l与AB垂直.

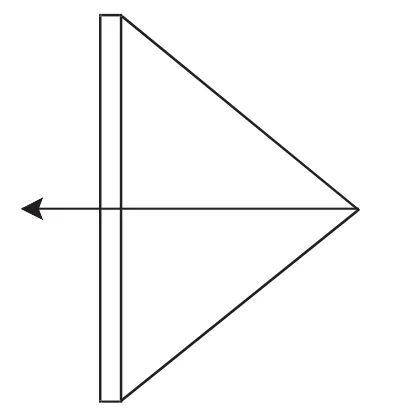
图3

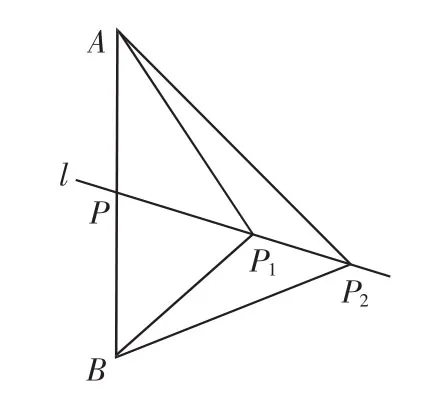
图4

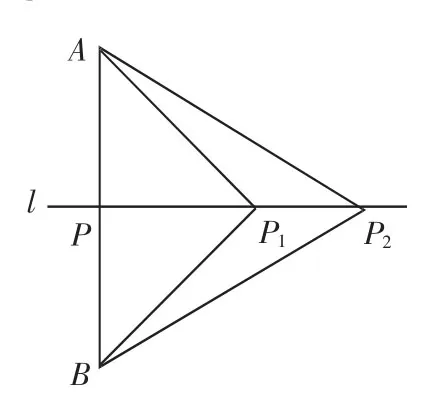
图5

2.讨论：要使l与AB垂直，AP1、AP2、BP1、BP2应满足什么条件？图5中，只要使箭端到弓两端的端点的距离相等，就能保持射出箭的方向与木棒垂直，从而拉开了线段垂直平分线性质逆命题的教学序幕.

动手操作在代数教学中表现为学生历经数的运算、实验、观察、猜想、感悟及论证等系列活动，同样它蕴含着发现的成份.

在动手操作中，对于具体的操作和活动而言，不能让动手操作过程去替代学生的思维过程.提升思维最终要通过“活动的内化”去完成.活动是一个载体，目的是让学生感悟、理解知识，实现知识的“再创造”过程.

四、寓新课序幕于兴趣式的问题情境中

其实质就是动机迁移.在今天学生普遍缺乏数学学习兴趣的情况下，教师可以利用他们喜欢玩游戏、爱听故事、好踢足球、打台球的兴趣，把它们迁移到学习上来，从而实现由直接兴趣向间接兴趣的转化.学生好动、好玩，是天性，又是活力，教师应鼓励学生在玩中动脑，玩出“学问”.当今媒体广泛，玩的东西甚多，怎样将这些东西转变为学生学习的一种兴趣“资源”，是值得我们数学教师在教学中去不断地思考的课题.

案例6 在直线上找一点，使它到这条直线同旁两点的距离和最短.这是由教材中的引例建立起来的数学模型，笔者开动脑筋，抓住男生打台球的喜好，将教材中的问题情境进行了“置换”：

如图6，四边形ABCD是长方形台球桌的台面，有黑白两球分别位于E、F两点位置上.试问：怎样撞击黑球E先碰撞台边CD反弹后再击中白球F？

学生对此兴趣浓厚，纷纷踊跃回答，但又都说不出理由.此时，学生急于想知道答案，正好处于欲进不得，欲罢不能的状态.然后，笔者说：“通过这节课的学习，答案就能解决了”.

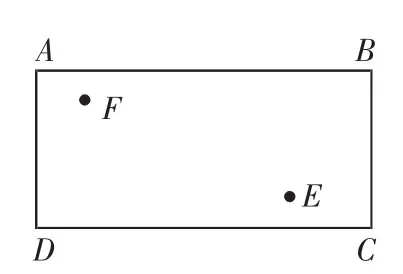
图6

案例7 某地出土一明代残破圆形瓷盘，如图7所示.请问用什么方法能复制该瓷盘？

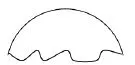
图7

分析：欲复制该瓷盘，需确定其圆心和半径.圆心到圆上各点的距离相等，因此，圆心必然在圆上任意两点连线的垂直平分线上，由此拉开了“过三点的圆”的序幕.学生对出土文物颇有一种好奇心，学生自然就会有一股“钻”的劲头.

五、寓新课序幕于类比的问题情境中

类比是一种由特殊到特殊的推理，它具有广泛的迁移性.波利亚高度评价类比的作用，指出：“类比是提出新命题和获得发现取之不竭的源泉”.很多数学知识结构类似，探究方法类似.若以类比式切入，学生易于接受，使学生不仅收获了知识，更获取了思维的方式.

案例8 等腰梯形的性质与判定就是通过类比等腰三角形的性质与判定来拉开序幕的，从中猜想、论证.这是基于图形之间的内在联系，因为等腰梯形可从等腰三角形中截取，这是“形状”的类比.

案例9 在学完积的算术平方根的性质一节后，有的学生联想到和、差、商的算术平方根是否也有类似的性质，这时，笔者不失时机地抓住学生类比猜想的机会，将其布置成课下作业，让学生通过数据验证其联想是否成立.这是“方法”的类比.

案例10 如图8，是一个平分角的仪器，其中AB=AD，BC=DC.将点A放在角的顶点，AB和AD沿着角的两边放下，沿AC画一条射线AE，AE就是角平分线.你能说明它的道理吗？

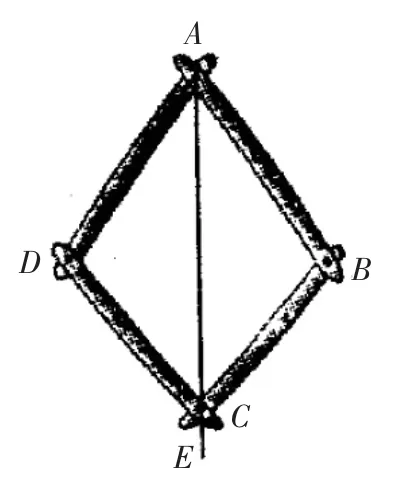
图8

分析：以仪器为“模型”，能为学生研究角平分线的作法提供联想和启示.

在问题的类比中，要注重引导学生发现问题和提出问题.因为学生们的提问往往会给教师拉开新课序幕提供“素材”.从创新的角度讲，学生发现、提出一个富有思考价值的问题，往往要比解决一个问题更重要.但是必须注意，类比与不完全归纳一样，都是似真推理，类比猜想的结果必须要经过检验证明.

六、寓新课序幕于特殊化的问题情境中

唯物辩证法指出：“事物的普遍性和特殊性既相互联系，又相互转化.”对特殊化的图形、式，学生易于观察并发现其中的结论.这时，教师以此为起点，将其延伸到一般情形，从中探究是否会有同样的结论.以特殊性为导入，并推广到一般化，体现了循序渐进的教学原则，符合学生的认识特点.在这种方式中，学生将体验到分类、联想、转化和归纳等学习方式以及唯物辩证法的思想.

案例11“圆周角定理”一节就是由圆周角的一边经过圆心这一特殊性得出的结论为切入点来拉开新课序幕的.以此为起点，再去探究圆周角和圆心的另外两种位置关系中是否有同样的结论，最后归纳得出圆周角定理.

七、寓新课序幕于逆向式的问题情境中

正向思维和逆向思维是人类思维的两种方向.逆向思维是把问题反方向探索，“反其道而行之”，体现了思维的灵活性，闪烁着创新的火花.事实上，数学知识本身就充满着正逆两方面的转化，如：乘方运算与开方运算，整式乘法和因式分解，命题与逆命题等.一般说来，学生习惯于正向思维，而忽视逆向思维，在学习中加强这方面的训练是十分必要的.某些图形的性质和判定，存在着互逆性，某些数、式运算的公式、法则也存在着互逆性.若将这些知识采用逆向思维方式导入拉开新课序幕，则既能温故，又可知新.

案例12“平行四边形的判定”一节就是在复习平行四边形性质后，将题设、结论颠倒位置，再由学生探究新命题是否成立来拉开新课序幕的.

寓新课序幕于问题情境之中的七种导入方式都有引导学生质疑、探究的功能.营造新课序幕导入情境的方式很多，其关键就是要创造最佳的课堂气氛和环境，为学生能顺利接受新知创造有利条件.问题情境的导入既要服务于具体的教学内容，又要充分考虑学生的客观实际，如知识面、求知欲、学习水平、存在问题等智力因素和非智力因素，要把趣味性和启发性有机地结合起来，激起学生相应的情感，在兴奋中进入角色，领会新知，要力争用最贴切的形式，迅速在师生之间架起一座通畅的交流知识与情感的桥梁.