由两个简单结论引发的对一道竞赛题的探究
2013-07-25河北省围场县天卉中学
☉河北省围场县天卉中学 赵 平
结论一:角平分线+垂线⇒等腰三角形(及底边的中点).
具体理解:如图1,OP是∠MON的平分线,AB⊥OP,分别交OM、ON于点A、B.则有以下结论成立:①OA=OB;②点C是AB的中点.即△AOB是等腰三角形,垂足是等腰三角形底边的中点.特别说明:结论②用的更多一些.证明比较简单,这里从略.
结论二:直角三角形一个锐角的平分线与斜边上的高线以及该锐角的对边围成等腰三角形.

图1
具体理解:如图2,已知△ABC中,∠ACB=90°,AB边上的高线CH与△ABC的一条角平分线AM相交于点P.求证:CM=CP(△CMP是等腰三角形).

图2
简析:由AM平分∠CAB,知∠CAM=∠BAM.
又∠BAM+∠APH=90°,∠CAM+∠AMC=90°,
则∠AMC=∠APH=∠CPM,
即△CMP是等腰三角形.

图3
引申:把直角三角形一个锐角的平分线换为该锐角的外角平分线,结论仍然成立.如图3,若AM是Rt△ABC的锐角∠CAB的外角平分线,且AM交BC的延长线于点M,交AB边上的高线的延长线于点P,则△CMP是等腰三角形.证明方法同上,这里从略.
竞赛题 (2009年全国初中数学联合竞赛(B卷)第二大题)已知△ABC中,∠ACB=90°,AB边上的高线CH与△ABC的两条内角平分线AM、BN分别交于P、Q两点,PM、QN的中点分别为E、F.求证:EF∥AB.
原解:如图4,因为BN是∠ABC的平分线,
所以∠ABN=∠CBN.
又因为CH⊥AB,
所以∠CQN=∠BQH=90°-∠ABN=90°-∠CBN=∠CNB,故CQ=NC.

图4
又F是QN的中点,
所以CF⊥QN,
所以∠CFB=90°=∠CHB,
因此C、F、H、B四点共圆.
又∠FBH=∠FBC,所以FC=FH,
故点F在CH的中垂线上.
同理可证,点E在CH的中垂线上.
因此EF⊥CH.又AB⊥CH,所以EF∥AB.
一、从两个结论对解法进行探究
由两个结论想到不同于原证法的证明方法,而且不用四点共圆,降低难度.
在图3中,由结论二可知△CMP及△CNQ均为等腰三角形,而点E、F分别为两个等腰三角形底边上的中点,若分别连接CE、CF,则有CE⊥AM,CF⊥BN.分别延长CE、CF与AB相交,则可知点E、F分别所得线段的中点,所以线段EF为所得三角形的中位线,从而结论得证.
证明:如图5,分别延长CF、CE与AB相交于点G、D.
因为CH是AB边上的高线,∠ACB=90°,AM平分∠CAB,所以∠HAP+∠APH=90°,∠CAP+∠CMA=90°,∠HAP=∠CAP.
所以∠APH=∠CMA=∠CPM,即CM=CP.
又点E是PM的中点,
所以CD⊥AM.
又AM平分∠CAB,
所以△ACE≌△ADE.

图5
所以点E是CD的中点.
同理点F是CG的中点.即EF是△CDG的中位线.
所以EF∥DG,即EF∥AB.
二、由结论二的引申对问题进行变式探究
结论二的引申:把内角的平分线换为外角的平分线,结论不变.那么,竞赛题中若把角的平分线换为外角的平分线,结论是否也不变呢?下面我们来探究一下:
1.把一条内角的平分线换为外角的平分线
如图6,已知△ABC中,∠ACB=90°,AB边上的高线CH与△ABC的一条外角平分线AM、一条内角平分线BN,分别交于P、Q两点,PM、QN的中点分别为E、F.求证:EF∥AB.

图6
证明:如图6,分别延长CF、CE与AB所在的直线相交于点G、D.
因为CH是AB边上的高线,∠ACB=90°,AM平分∠DAC,
所以∠HAP+∠APH=90°,∠CAM+∠CMA=90°,∠HAP=∠DAM=∠CAM.
所以∠APH=∠CMA,即CM=CP.
又点E是PM的中点,所以CD⊥PM.
又AM平分∠CAD,
所以△ACE≌△ADE.
所以点E是CD的中点.
同理,点F是CG的中点.
即EF是△CDG的中位线.
所以EF∥DG,也即EF∥AB.
2.把两条内角的平分线都换为外角的平分线
如图7,已知△ABC中,∠ACB=90°,AB边上的高线CH所在的直线与△ABC的两条外角平分线AM、BN所在的直线分别交于P、Q两点,PM、QN的中点分别为E、F.求证:EF∥AB.
证明:如图7,分别延长CF、CE与AB所在的直线相交于点G,D.

图7
因为CH是AB边上的高线,∠ACB=90°,AM平分∠DAC,所以∠HAP+∠APH=90°,∠CAM+∠CMA=90°,∠HAP=∠DAM=∠CAM.∠APH=∠CMA,即CM=CP.
又点E是PM的中点,所以CD⊥PM.
又AM平分∠CAD,所以△ACE≌△ADE.
配制一系列不同初始浓度的甲基紫溶液,其他条件不变,考察甲基紫溶液初始浓度对TiO2薄膜光催化性能的影响,实验结果见图4.
所以点E是CD的中点.
同理,点F是CG的中点.即EF是△CDG的中位线.
所以EF∥DG,也即EF∥AB.
三、对母题所产的“金蛋”进行探究
关于“费尔马猜想”这个问题,有一个有趣的传说,伟大的数学家希尔伯特曾经声称,他能解开这个难题,可是由于在求解这个难题的过程中,给数学的发展创造了不少新的内容,如果这个难题解决,这些有益的副产品就可能得不到,因此他故意回避而不去解决,他很形象地将“费尔马猜想”比作一只母鸡,而将那些有益的副产品比作“金蛋”,希尔伯特深情地说“我应当更加注意,不要杀掉这只经常能为我们下金蛋的母鸡.”相信这样一道优质的赛题也一定会产出一些金蛋.不探究一番,实在可惜.
第一枚金蛋.如图8,已知在△ABC中,∠ACB=90°,AB边上的高线CH与△ABC的一条角平分线AM相交于点P,又点E、D分别为PM、AC的中点.求证:ED∥AB.

图8
简析:由结论二知点E为等腰三角形CMP的底边中点,所以CE⊥AM.又点D为AC的中点,所以ED是Rt△ACE斜边的中线,即DE=AD=CD,所以∠AED=∠DAE=∠EAB,问题得证.
第二枚金蛋.如图9,已知在△ABC中,∠ACB=90°,AB边上的高线CH与△ABC的一条角平分线AM相交于点P.又点E、D分别为PM、AC的中点,连接DE、DH.求证:DE=DH.

图9
因为DH是Rt△ACH斜边的中线,
所以DH=AD=CD,
即DH=DE.证毕.
第三枚金蛋.如图10,已知△ABC中,∠ACB=90°,AB边上的高线CH与△ABC的两条内角平分线AM、BN分别交于P、Q两点.PM、QN的中点分别为E、F,若AC=3,BC=4.求EF的长度.
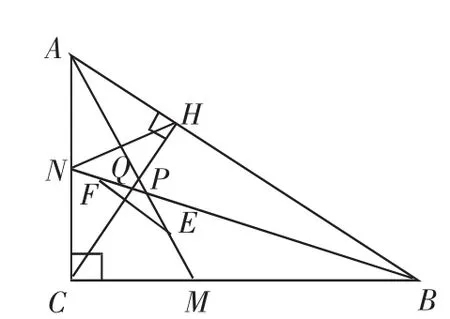
图10

图11
简析:如图11,分别延长CF、CE与AB相交于点G、D.
根据赛题的证明,再结合结论一:
由CE⊥AM,可得△ACD是等腰三角形,所以有AC=AD.由CF⊥BN,
可得△CBG是等腰三角形,
所以有CB=BG.
根据图形知DG=AD+BG-AB,
所以DG=AC+BC-AB.
又EF是△CDG的中位线,
