解析几何初步中“坐标法”的“凸显”
2013-07-25湖南省株洲县五中方厚良
☉湖南省株洲县五中 方厚良 罗 灿
这些年,笔者时常忆起2004年上海高考的第11题“教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的本质是______.”(答案:用代数的方法研究图形的几何性质).这道绝无仅有的“文科式”的考题引发了笔者长期的思考:如今的数学似乎就意味着解题,尤其是考试题,就是数字、就是计算或推理,而深层次的数学思想、文化、精神和力量却很难体现,甚至缺乏基本的引导.2004年上海的这道考题,不是说它对数学的文化、精神体现得如何充分,难能可贵的是开了这方面探究的先河,其意义在于引发对数学本质的多元思考,引发数学教学的某些缺失反思.“解析几何初步要凸显‘坐标法’”的观念就是这一思考的产物,教学不应是知识的简单堆砌,也不是习题的机械操练,而应在知识的理解和习题内化过程中体悟数学的文化、思想和精神,抓住了“坐标法”就抓住了解析几何的核心和灵魂,而且其力量还可渗透、迁移到函数、向量和立体几何等学科.
一、章引言课以数学史为载体,从学科本质高度凸显“坐标法”
在初中,数轴上的点与实数、直角坐标平面上的点与有序实数对的一一对应使学生对“坐标”概念有了基本认识,对于用坐标刻画位置有了基本印象;通过对一次函数、反比例函数和二次函数等常见函数的学习,学生获得了“描点作图”这一宝贵经验.
高中必修1模块对函数基本性质及指、对、幂三类基本函数学习,深化了数形结合思想,当然也体现了坐标法.
在必修2模块开设“解析几何初步”(“直线与方程”和“圆与方程”两章)的意义,主要是还原数学史,凸显坐标法的历史地位,从方法论的高度彰显其价值.所以,进入该内容学习,有必要组织一节“引言课”,回顾上述学习过程,体味内隐的“坐标法”思想,组织学生阅读教材[1]第81、82页目录与引言,获得“坐标法是解析几何中最基本的研究方法”和“用代数的方法研究图形的几何性质”的基本认识,从整体上把握这门学科的特点和本质;指导阅读第111页“笛卡尔与解析几何”和第124页“坐标法与机器证明”两处“阅读与思考”材料,首先,经历感受坐标法产生的历史背景、发展历程:从17世纪笛卡尔“放弃仅是练习思想的抽象几何,寻找普适性方法论意义的代数化”坐标法的诞生,到牛顿、莱布尼茨基于坐标法下微积分的创立,再到20世纪我国数学家吴文俊的机器证明的“吴方法”;其次,认识坐标法的重要意义和价值:这里名家名言的影响很重要,教师要有意识突出这些对坐标法的评价话语,如恩格斯“数学中的转折点是笛卡尔的变数,有了变数,运动进入了数学,有了变数,辩证法进入了数学,微分和积分也立刻成为必要的了”,并将笛卡尔的坐标法、牛顿和莱布尼茨的微积分和对数的发明并称为17世纪自然科学的三大发明;最后,对于学有余力和对数学特别感兴趣的学生,教师可推荐相关对坐标法介绍的书籍进行课外阅读,如M.克莱因的《古今数学思想》的第15章“坐标几何”、斯科特的《数学史》第7章“17世纪几何学的新方法”等的相关章节都写得深刻而又精彩,是比较理想的阅读材料.总之,引言课的学习,应给学生奠定对解析几何这门分支的内容、方法和意义的基本认识、熏陶和濡染,并继续在后续学习中作更进一步的引导、渗透和深化.
二、概念辨析、公式推导为契机,在细节处体会“坐标法”

三、如何求直线点斜式方程?精妙全在“坐标法”
笛卡尔坐标法的“野心”应该深刻在每个学习数学(尤其是解析几何)的人的心头:把一切问题归结为数学问题,把一切数学问题归结为代数问题,把一切代数问题归结为方程,最后得到关于一个未知数的方程.方程的“翅膀”使得几何研究得以腾飞.而直线点斜式方程是用坐标法推导出的第一个“曲线方程”,是方程的翅膀的第一次飞翔,是为今后更多曲线方程飞翔的示范.在这之前,学生没有推导曲线方程的经验,甚至没有“直线的方程”和“方程的直线”这两个基本概念,所以,“直线的点斜式方程”这节课如何上、如何挖掘其蕴含的深刻思想、观念就很重要而且富于意义.笔者作了以下几点尝试:
(1)介绍笛卡尔的“野心”激活学生学习探究的“野心”;
(2)编拟问题串:在直角坐标系内确定一条直线的几何要素是什么?(一点和倾斜角(斜率))构成几何图形(直线也不例外)最基本的“单元”是什么?(尝试引导将线化归为点,进而与坐标对应)什么是方程及能用直线上的点来建立直线的方程吗?(方程是“含未知数的等式”;将直线理解为其上动点P(x,y)的轨迹正如恩格斯所说“笛卡儿变数”,为直线方程建立指明方向,即“将直线上所有点的坐标(x,y)满足的等量关系表示出来”即可,更进一步,所谓曲线的方程的建立就是曲线上任意一点满足的“含未知数的等式”的坐标翻译.)
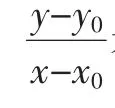
四、证明几何问题,展示“坐标法”的经典“三部曲”
坐标法之所以称为大法,在于它可以和平面几何问题、向量方法都可以建立联系,可以推广到空间去解决立体几何问题.在解析几何初步主要体现在用坐标法解决平面几何问题,是为经典的“三部曲”:
第一,建立适当的直角坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
第二,通过代数运算,解决代数问题;
第三,把代数运算结果“翻译”成几何关系.
虽然“三部曲”很具程序性,应该便于操作,但教学实践发现,学生运用起来还是问题不少,既有思想内核的领悟还有待深化,也有细节技术的粗糙有待打磨.下面通过例子来说明.
案例1 已知点O是△ABC边BC的中点,求证:

此题是教材第110页习题3.3B组题7.教学时被选为教材第105页例4“证明平行四边形四条边的平方和等于两条对角线的平方和.”的变式习题.但学生的解答很不理想,主要有以下问题:
问题1:“适当”建系理解不够,随意性大,不能兼顾特殊性与一般性.
如只注意一般性,设A(a,b)、B(c,d)、C(e,f);太特殊化,将△ABC设为等腰三角形或直角三角形“方便”建系:△ABC为等腰三角形则以O为原点,BC边所在直线为x轴,设A(0,b)、B(-a,0)、C(a,0);△ABC为直角三角形时以A为原点,AB、AC边所在直线分别为x轴和y轴,设A(0,0)、B(a,0)、C(0,b).
理论上建系是具有多样性的,但有一点是肯定的:不同的建系会使点的坐标参数的个数呈现差异、曲线方程存在繁简之别,而且直接影响后续代数运算量.学过解析几何的都深知一个“算”字了得!所以“适当”二字是需要玩味和积累的,譬如对称性的利用.
问题2:步骤凌乱“,三部曲”不明显.
有不建系的;有的画一个直角坐标系,不交代如何建系,如以哪点为原点,谁为坐标轴,甚至“如图建系”都没有,当然也有简到仅“如图”二字的“;把代数运算结果‘翻译’成几何关系”也时常被丢掉.
案例2 已知0<x<1,0<y<1,求证:
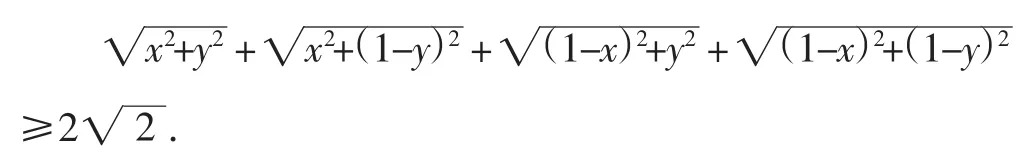
此题是教材第110页习题3.3B组题8,左边式子虽然具有明显的几何意义,但仍有不少学生“看不出”这种“距离结构”,正所谓“会者不难,难者不会”,不过我们不能只是抱怨,更不能放弃,这说明要学生真正灵活掌握“坐标法”还有很多事要做,要给学生丰富的体验和经验积累.
总的来说,坐标法作为中学数学的一个大法,对它的学习和领悟可能需要足够多的时间、足够多的材料滋长浸润,解析几何初步作为坐标法的正式“入门”课程,既可能实现“好的开始是成功的一半”,也要做足“万事开头难”的充分准备,但凸显“坐标法”的深远意义是毋庸置疑的.
1.王申怀.数学2[M].北京:人民教育出版社,2011.
