对2013年湖北高考数学《考试说明》的研究与思考
2013-07-25湖北省武汉市黄陂六中
☉湖北省武汉市黄陂六中 梅 磊
湖北省教育考试院《2013年普通高等学校招生全国统一考试大纲(湖北卷)数学科考试说明》(以下简称“《考试说明》”)不仅是2013年湖北高三教师和学生复习备考的重要资料,同时也是2013年湖北高考数学命题的主要依据.学习研究《考试说明》,明确其强化什么,淡化什么,突出什么,回避什么,对明晰考试要求和把握复习方向有重要意义.
《考试说明》共分考试性质、命题指导思想、考核目标与要求、考试范围与要求层次、考试形式与试卷结构和题型示例5个部分,其中考核目标与要求部分对数据处理能力的考查,对数学基础知识的考查,对数学思想和方法的考查,对数学能力的考查的表述与2012年略有调整,考试范围与要求层次部分对具体内容及层次要求略有调整,题型示例部分有所调整.
一、关于数学知识的考查
《考试说明》的表述是:对数学基础知识的考查,既全面又突出重点,注重学科的内在联系和知识的综合.注重试题的基础性、综合性和层次性.合理调控综合程度,坚持多角度、多层次的考查.对知识的要求由低到高分为了解、理解、掌握三个层次.
与2012年相比,《考试说明》在考试具体内容及层次要求中,有以下一些变化:
(1)三角函数中“诱导公式、同角三角函数的基本关系式”由“理解”变为“掌握”.
解读:对“诱导公式、同角三角函数的基本关系式”考查要求由“理解”变为“掌握”后,三角变换的四组公式:诱导公式、同角公式、和差公式、倍角公式的考查要求均为“掌握”,说明三角变换相对提高了要求.这是因为对于三角变换,试题的复杂程度较之以前已明显降低,而考生的作答情况则随着试题变得简单而越来越不尽如人意,特别是2012年湖北高考文科第18题实测难度仅为0.39,意外成为难题.
建议:三角变换的目的是化简,化简的最终结果是为了把问题本质的东西更好地体现出来,所以复习中要弄清三角变换的目的、思路和方法,准确把握变换目标、变换对象,从宏观上把控变换方向.一切为实现目标服务,避免机械、盲目地套用公式.只有理解了变换的目的,才能做恰当的变换.
参考题:人教A版课本必修4第147页A组第9-12题,B组第6题.
(2)三角函数中“了解周期函数的定义、三角函数的周期性”改为“了解周期函数的定义”.
解读:去掉了“三角函数的周期性”的特指,说明对一般函数的周期性也有所要求,更符合近几年湖北考题实际.
建议:按照《考试说明》要求:了解周期函数的定义,能够“按照一定的程序和步骤照样模仿”,要注意一般函数的周期性.
参考题:人教A版课本必修4第46页A组第10题,B组第3题.

建议:需要强调的是,人教A版课本选修4-5第9页用黑体字给出了一般形式的算术—几何平均不等式,第53页“探究”提供了证明一般形式的算术—几何平均不等式的一种方法.
参考题:2011年湖北高考理科第21题,2012年湖北高考理科第22题.
(4)导数及其应用中,“常见基本初等函数的导数公式”加注“*”号,并在表后附有8个公式.
解读:借鉴其他省市的做法,《考试说明》附注8个常见基本初等函数的导数公式,避免了其他公式是不是常见基本初等函数的导数公式的争论.
建议:不要求根据导数定义推导这些公式,只要求能够利用它们求简单的函数的导数即可.在复习中,适量的练习对于熟悉这些公式的运用是必要的,但应避免过量的形式化的运算练习.
参考题:人教A版课本选修1-1第85页A组第4题(选修2-2第18页A组第4题).
(5)导数及其应用中,“利用导数研究函数的单调性”和“函数的极值、最值”由“理解”变为“掌握”,并去掉了“多项式函数一般不超过三次”的限制.
解读:导数在中学阶段的定位就是以研究函数单调性为核心的,这是与导数的定义相关的.函数单调性与函数的最值以及发展趋势有着必然联系,因此在利用导数求函数单调性的问题中也提出会求函数极大值与极小值的要求以及闭区间上最大值与最小值的要求.“利用导数研究函数的单调性”和“函数的极值、最值”由“理解”变为“掌握”,说明“利用导数研究函数的单调性和极值、最值”提高了要求,去掉了“多项式函数一般不超过三次”的限制,说明可能考查四次函数和五次函数等.
建议:需要强调的是,函数的单调性与导数的关系,利用导数求函数的极值、最值方法在人教A版课本选修2-2(选修1-1)都是用黑体字给出的.要掌握课本上利用导数研究函数的单调性、极值和最值的方法,以及利用函数的单调性、极值和最值证明不等式的方法.值得注意的是,可能考查四次函数和五次函数,这在其他省市高考试卷中考查过.
参考题:2007年重庆理科第20题,2008年天津文科第21题,2008年江西文科第21题,2008年湖南文科第21题,2008年四川文科第20题,2009年全国Ⅰ文科第21题,2010年全国Ⅰ文科第21题.
(6)圆锥曲线中,“双曲线的定义及标准方程”和“双曲线的简单几何性质”由“了解”变为“理解”.
解读:近年来,高考对双曲线的考查要求不断降低,从“掌握”到“理解”再到“了解”,导致考生的作答情况越来越不尽如人意,《考试说明》提高对“双曲线”的要求,对湖北高中数学教学有导向作用.
建议:要让学生真正理解双曲线的定义及标准方程和简单几何性质,注意双曲线与椭圆的区别与联系,注意等轴双曲线和黄金双曲线等特殊的双曲线.
参考题:人教A版课本选修2-2第60页例6,2012年湖北高考理科第14题.
(7)概率与统计中,“用样本的频率分布估计总体分布,用样本的基本数字特征估计总体的基本数字特征”由“掌握”变为“理解”.
解读:对“用样本估计总体”的要求,由“掌握”变降低为“理解”,与前面两个相关考点的要求保持一致,更符合《课程标准》的要求.
建议:结合生活化背景考查频率分布表、频率分布直方图和茎叶图是高考的热点,其方式主要是理解频率分布表、频率分布直方图和茎叶图,并由图、表得到数据相关信息,在此基础上考查频率、频数、样本容量,并与概率或其他知识交汇考查,要引起重视.另外,众数、中位数、平均数是初中就学了样本数据的基本数字特征.值得注意的是,高中课本新增了从频率分布直方图中估计样本的众数、中位数、平均数.
参考题:2012年湖北高考文科第5题.
要仔细推敲《考试说明》对考试内容三个不同层次的要求,准确掌握哪些内容是了解,哪些是理解,哪些是掌握,值得指出的是《考试说明》中对知识要求的三个层次表示的是在所考查的知识点上对考生要求的程度,并不代表有关该知识点的考题是以小题还是以大题的形式出现.应严格按照《考试说明》中所规定的具体内容和层次要求去备考,不能随意提高或降低复习要求,更不能随意扩大或缩小复习范围,这样既能明了知识系统的全貌,又可知晓知识体系的主干及重点内容.
二、关于数学能力的考查
《考试说明》的表述是:能力是指空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识.对数学能力的考查,以抽象概括能力和推理论证能力为核心,全面考查各种能力.注意问题的多样化,体现思维的严谨性、抽象性和发散性.
与2012年相比,《考试说明》继续强调“以抽象概括能力和推理论证能力为核心,全面考查各种能力”,增加了“体现思维的严谨性、抽象性和发散性”的表述.
解读:以抽象概括能力和推理论证能力为核心,要求能在对具体的实例抽象概括的过程中,发现研究对象的本质;从足够的信息材料中,概括出一些合理的结论.会根据已知的事实和已获得的正确数学命题来论证某一数学命题的正确性.增加了“体现思维的严谨性、抽象性和发散性”的表述,突出了《课程标准》中指出的数学在形成人类理性思维和促进个人智力发展的过程中发挥着独特的、不可替代的作用,凸显了《课程标准》中注重提高学生的数学思维能力的基本理念.
建议:在运用数学解决问题时,要让学生不断地经历直观感知、观察发现、归纳类比、空间想象、抽象概括、符号表示、运算求解、数据处理、演绎证明、反思与建构等思维过程.这些过程是数学思维能力的具体体现,有助于学生对客观事物中蕴含的数学模式进行思考和做出判断.
参考题:2011年湖北高考理科第5题.
给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如下图所示:
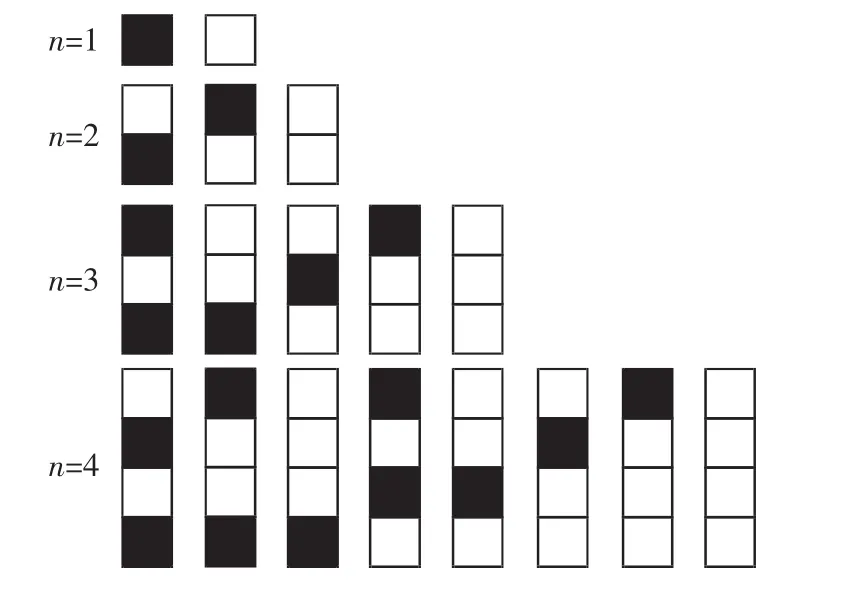
由此推断,当n=6时,黑色正方形互不相邻的着色方案共有______种,至少有两个黑色正方形相邻的着色方案共有______种.(结果用数值表示)
本题满分5分,实测平均分0.97分,难度0.19,低于压轴题难度0.25,意外成为全卷最难题.在258075名理科考生中竟然有192168人得0分.很多考生不能正确理解题意,不能发现数列的构成规律,误将本题中的数列认为是二阶等差数列,当n≤4时,2,3,5,8也符合二阶等差数列,但只要多想一步,看一看当n=5时的情况,就知道此题中的数列不是二阶等差数列,而是斐波那契数列.绝大多数考生没有意识到第一空的结果与第二空的结果相加的和应等于当n=6时的所有着色方案种数26,这些都是出乎命题组意料之外的.
三、关于数学思想和方法的考查
《考试说明》的表述是:对数学思想和方法的考查,与数学知识融合,从学科整体意义和思想含义上立意,注重通性通法,淡化特殊技巧.
与2012年相比,《考试说明》继续强调“注重通性通法,淡化特殊技巧”,删除了“数学思想和方法是数学知识在更高层次上的抽象和概括”的表述.
解读:“注重通性通法,淡化特殊技巧”是多年来数学《考试说明》中坚持的响亮口号,每年的试卷都基本体现了这一指导思想.删除了“数学思想和方法是数学知识在更高层次上的抽象和概括”的表述,只是为了与《考试说明》前一段“对数学基础知识的考查”和后一段“对数学能力的考查”的表述相协调,并不意味着否认数学思想和方法是数学知识在更高层次上的抽象和概括.数学思想方法属于方法范畴,但更多地带有思想、观点的属性,属于较高层次的提炼概括.在高考考查中,共识的数学思想有函数与方程思想,数形结合思想,分类与整合思想,化归与转化思想,特殊与一般思想,有限与无限思想,或然与必然思想;基本数学方法有待定系数法,换元法,配方法,割补法,反证法,数学归纳法等,它们是数学通法的主体;数学逻辑方法或思维方法有分析与综合,归纳与演绎,比较与类比,具体与抽象等,它们都是数学考查中理解、思考、分析与解决问题的普通方法.
建议:在系统复习基础的时候,学生仅仅有知识的积累还不够,还要注意思想的领会和方法的归纳,特别是化归与转化的思想和分析与综合的方法,研究通性通法.这些思想和方法的获得,又全在于学生对数学知识网络的准确把握与灵活运用.要想方设法让学生熟练地掌握数学思想方法的适用情境,这样才能在陌生的情境中想到它、运用它.
参考题:2012年湖北高考理科第22题.
(Ⅰ)已知函数f(x)=rx-xr+(1-r)(x>0),其中r为有理数,且0<r<1,求f(x)的最小值;
(Ⅱ)试用(Ⅰ)的结果证明如下命题:

(Ⅲ)请将(Ⅱ)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题.
注:当α为正有理数时,有求导公式(xα)′=αxα-1.
本题第(Ⅰ)问,实际上是证明贝努利不等式的一种,而贝努利不等式在课本选修4-5第52页例3后的说明中出现,利用导数求函数的最值也是课本上的常规方法.但较多考生根据求导结果可以得到f′(x)=0,即得出当x=1时,f(x)取最小值,讨论过程错误频现,体现出对基本概念、基本方法并未掌握.
本题第(Ⅱ)问,实际上证明杨不等式的一种,虽然杨不等式在课本上没有直接出现,但是寻找第(Ⅰ)问与第(Ⅱ)问的内在联系,利用第(Ⅰ)问证明第(Ⅱ)问是考生熟悉的方法.但不少考生看不出寻找第(Ⅰ)问与第(Ⅱ)问的内在联系,盲目拼凑出要证的结论,体现出对转化与化归思想并未掌握.
本题第(Ⅲ)问,实际上证明加权均值不等式,而加权均值不等式的特例n个正数的均值不等式在课本选修4-5第53页例4后的“探究”中出现,数学归纳法也是课本上的常规方法.但部分考生完全不能理解题意,生搬硬套写出一般形式,出现明显的“假证”现象,体现出对数学归纳法并未掌握.
四、关于题型示例
《考试说明》的表述是:为让考生对高考试题获得一定的认识,我们从近几年高考数学湖北卷试题和其他省市的高考试题中选择了部分试题编制成题型示例.题型示例中的试题与2013年高考试卷的结构、形式、测试内容、题目排序、题量、难度等均没有任何对应关系.
与2012年相比,《考试说明》对示例试题有些调整,如下表:
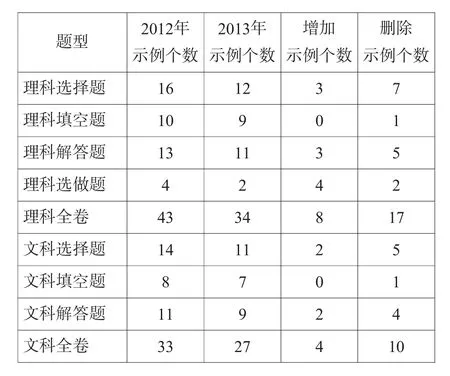
解读:题型示例新增的12个示例均是2012年湖北高考试题,体现了《考试说明》的与时俱进,说明了课程改革与高考改革的一致性.值得商榷的是,题型示例中理科“试题29”和文科“试题4”及“试题26”,都涉及椭圆的准线概念,这与《课程标准》的教学要求和《考试说明》的考查要求并不一致.
建议:需要强调的是,题型示例中的试题与2013年高考试卷的结构、形式、测试内容、题目排序、题量、难度等均没有任何对应关系,只是为让考生对高考试题获得一定的认识.值得注意的是,题型示例中每道试题后面的“说明”,它指出了该题考查的知识点和难易程度.另外要注意,题型示例中解答题每道试题后面的“答案”,它体现了通性通法和常规方法.
在复习备考过程中,我们要学习研究《考试说明》,明确2013年湖北高考在知识能力和思想方法考查方面的基本要求,准确把握湖北高考命题的方向和特点,做到科学备考.
