博观而约取，厚积而薄发——以e2－1为定值的圆锥曲线高考试题赏析

☉

物之生也，若骤若驰，无动而不变，无时而不移——《庄子·秋水》.数学问题千变万化，特别是历年的高考数学试题更是灵活多变，让很多学生望而生畏，在教学中我们如果能依据知识的特点，结合学生的具体实际，从系统的高度去剖析高考试题，寻找问题的本质，触类旁通，总结其内在的共性问题进行有效教学，对优化学生思维品质，减轻学生的学习负担，提高教学质量都是十分有益的.在近几年全国各地的圆锥曲线高考试题中就不断涌现出许多以k·1k2=e2-1为载体的精彩试题，是我们教学研究的重要素材，有必要引导学生去探究.

（

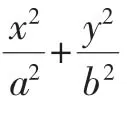
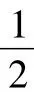
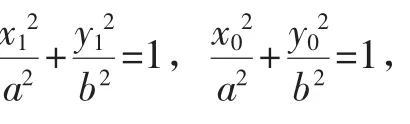
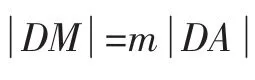
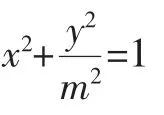
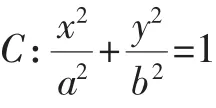
a＞b＞

0）相交于

A

、

B

两点，

P

为椭圆上任意一点，若线段

AB

被直线

OP

平分，设直线

AB

与直线

OP

的斜率分别为

k

1

与

k

2

，则

k

·

1

k

2

=e

2

-1.

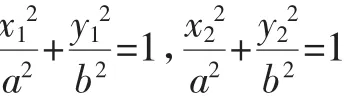
把①②代入③得：k·1k2=e2-1.

（1）求椭圆C的方程；

（2）求△APB面积取最大值时直线l的方程.

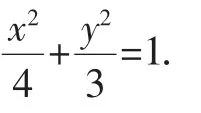
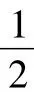
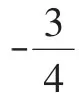
利用导数知识易求得当m=1-时，S△ABP最大，此时直线l的方程为：3x+2y+2-2=0.

证明：设A（x1，y）1，B（x2，y）2，线段AB的中点为M（x0，y）0，

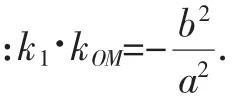
剖析试题共性的特点，一方面能培养学生洞察问题本质的智慧，有利于优化学生的思维品质，有利于遏制“题海战术”轻负高效，另一方面又能让学生从整体上把握知识的内在规律，拥有学习的智慧，有利于拓宽学生的学习视野，有利于激发学生的学习兴趣，有利于培养学生的应变能力，有助于完善学生的知识结构，提高学生的综合分析能力.

1.苏立标.探求以e2-1为定值的圆锥曲线问题［J］.中学数学教学参考，2006（5）.

2.玲珑居士.一道高考解几题的探究背景［J］.中学数学，2004（9）.