上好二轮复习课的几个着眼点——从一节数列复习课谈起
2013-07-25浙江省绍兴市第一中学
☉浙江省绍兴市第一中学 徐 萍
最近,笔者参与了学校组织的某省某重点中学高三数学二轮复习听课活动.听课之后感想很多,根据该省数列高考的重点与难点,笔者仅从一节数列通项的求法的复习课谈起.
一、教学片段

学生思考几分钟后,教师请学生代表回答此题.
生1:我想用递推来求解,但未观察出规律.
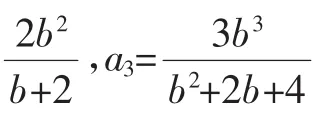

师:这是什么类型?用什么方法?
生(众):an=pan-1+q,用待定系数法an-λ=p(an-1-λ)转化为等比数列.
师:我们回忆一下求递推数列的通项还有什么类型,用什么方法求解.
师:(1)an-an-1=(fn),用累加法;
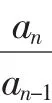
(3)an=pan-1+qn,两边同时除以qn转化为an=pan-1+q;
(4)用an与Sn的关系.
……
二、听课感想
高三二轮复习是在第一轮复习的基础之上,进行知识整合、方法归类、技能提高、思想提升的关键阶段.本节课讲解的是高考的重点与热点内容——数列通项的求法,教学目标明确.学生先练后讲,学生讲思路、讲困惑;教师启发引导,调动学生思考.但教学目标达成与否,效果如何,值得商讨.本节课教师虽然归纳了常见数列通项的求法,但学生是否掌握,掌握得如何,还有待检验.二轮复习课如何才能上得有效、高效是摆在高三数学教师面前的重大课题,值得反复研究,共同探讨.笔者认为要想上好高效的二轮复习课(以本节课为例),可从如下方面着手.
三、上好二轮复习课的几个着眼点
1.着眼于回归基础,构建知识网络
本节课所选例题,综合性较强,难度较大.用到了化归的思想,需要较强的观察问题、分析问题的能力.上课一开始就让学生探究,可能会误伤一部分同学的积极性.为此可设计一串基础题,让学生练习,然后引导学生回顾、提炼、总结归纳求数列通项的方法,形成知识网络.
设计题组为:
(1)数列{an}满足a1=2,an+1=3an,求数列{an}的通项公式.

(3)数列{an}满足a1=2,an+1=2an+3n,求数列{an}的通项公式.
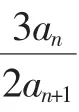
(5)数列{an}满足a1=2,a2=5,an+1=2an+3an-1,求数列{an}的通项公式.
设计意图:通过一组基础题训练,检验学生对基础知识的掌握情况,让学生提炼求数列通项的方法,构建知识网络.同时也为例题的讲解作好铺垫.
由于学生的学习具有遗忘性和缺陷性,二轮复习要注重基础知识的落实,要抓好数学知识的梳理,知识网络的构建,解题思想方法的归类.但是要引导学生自已构建,而不是教师代替学生归纳总结.
2.着眼于展示学生的思维,点拨评价
在课堂教学中要突出学生的主体地位是新课改倡导的理念.实践表明:采用“先练后讲,先思后讲,合作探究”的教学方法,可最大限度地减少教师的讲解时间,增加学生的动脑、动手、动口活动时间,提高教学效率.当发现学生思维有障碍时,要及时点拨,要善于发现学生思维的闪光点,并及时评价,鼓励,增强学生的自信心.因为在第二轮复习过程中,易出现“学习中的高原现象”,为此需要不断鼓励.

相信经过思考,就会有学生找到规律.这样通过老师的点拨,学生不仅学生会了如何观察,同时也能领会特殊到一般的思想.

教师可及时评价:生3同学的回答非常不错,他有多种解决问题的思路,并进行尝试.我们知道数学归纳法是求数列通项的重要方法,它的关键是先归纳猜想出通项,再用数学归纳法证明.要想归纳猜想正确必须做什么?能不能多算几个再归纳猜想呢?同学们可继续算一算a4,a5,再归纳猜想好吗?只要给学生时间,相信学生会解出此题的.
3.着眼于以错纠错,查漏补缺
二轮复习除抓基础知识的熟练掌握、知识网络的构建外,还要针对学生的疑难问题进行补救.学生在解题时,会出现错误,找不到解题思路和方法是很正常的.老师应帮助学生分析找不到思路或解题错误的原因,并加以训练,以达到“举一反三,触类旁通”的目的.
在讲解本例题时,教师会预想到学生碰到的困难.本题学生会遇到的困难为:
(1)分式结构不会变形或不会深入地变形;
(2)不会转换为an=pan-1+q的形式;

(4)利用数学归纳法解题时不会归纳猜想.其中重点和难点是:变形转换为常见数列,为此可设计如下习题进行变式训练:
变式1:在数列{an}中,a1=2,an+1=λan+λn+1+(2-λ)2(nn∈N*),其中λ>0.求数列{an}的通项公式.
设计意图:本题的解法具有多样性,如数学归纳法和递推的方法.用递推法时要引导学生分析思路:为什么要等式的两边同时除以λn+1,同时引导学生观察分析为什么可转化为等差数列,具体解法如下:
解法1:a2=2λ+λ2+(2-λ)2=λ2+22,
a3=λ(λ2+22)+λ3+(2-λ)22=2λ3+23,
a4=λ(2λ3+23)+λ4+(2-λ)23=3λ4+24.
由此可猜想出数列{an}的通项公式为an=(n-1)λn+2n.(用数学归纳法证明略)
解法2:由an+1=λan+λn+1+(2-λ)2(nn∈N*),λ>0,
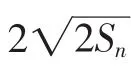
设计意图:遇到an与Sn的问题,学生大多想到消去Sn,但此题用此法行不通.为此要消去an,利用本题可纠正学生的思维定势,引导学生合理分析.当消去an时,还需要学生观察分析等式的特点,进行合理的变形.解题简要过程如下:当n≥2时,an+2=Sn-Sn-1+2=2,则Sn-2+2=Sn-1,()2(以下过程略).
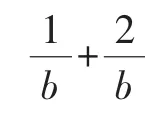

查漏补缺不仅要补大漏洞(如本题中的观察能力和转化能力),而且也不能放过小漏洞(如本题中将b分为b=2或b≠2进行分类讨论).二轮复习要注重细节,不轻易放过任何一个问题.只有将学生的缺漏补好,学生才会进步,才有提高.
4.着眼于变式探究,养成反思习惯,提升能力
讲完例题后,教师要引导学生养成反思的习惯.反思可以使知识形成网络,可以使方法得以内化,可以使缺陷得以补救,可以找到努力的方向和前进的动力,能力才能得以提升.
讲解完此题后,可以让学生思考:此题还有别的解法吗?可引导学生探究.
解法3:构造等比数列法.

解法4:迭代法.

设计意图:引导学生探究方法的多样性,可开拓学生视野,拓展思维,培养求异思维,构建知识与方法体系,提升解题能力.
探究完方法的多样性后,可构建新的情境,让学生学会将此方法进行迁移.如可作如下探索(可作为课堂练习或课后作业):

求数列{an}的通项公式.
设计意图:巩固观察变形能力,提升转化意识.简解如下.

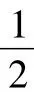
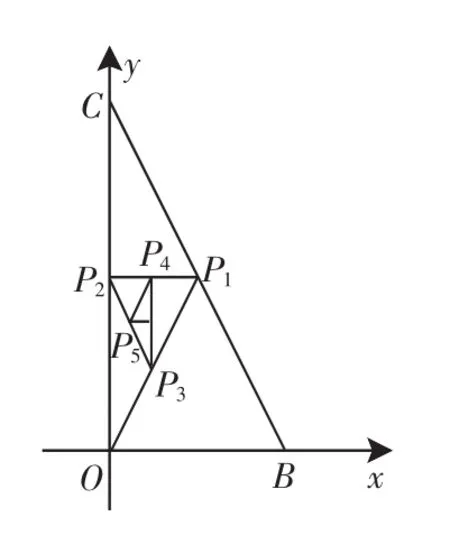
(1)求a1,a2,a3及an;

设计意图:转换新的情境,让学生学会思考、学会方法的选择,提升学生运用所学知识解决问题的能力.具体解法略.
总之,高三数学二轮复习的目的是:对高中数学知识系统梳理、形成知识网络;对一轮复习中存在的问题进行一定的补偿矫正;对主干知识进行重点突破;提升综合应用能力、应试水平.复习策略是:以学生为主体,让学生在课堂上尽情展示,成为课堂的主角.教师着重对学生进行有效的学法指导:教给学生反思学习的方法,形成反思习惯;教给学生自已查漏补缺、梳理知识、形成知识网络的方法;指导学生学会审题,利用好自己的“错误”;重视解题规范的培养,摆脱“会而不对,对而不全”的现象.
