例说根的判别式在压轴题中的隐形应用

☉江苏省南京市金陵中学河西分校 李玉荣

根的判别式Δ=b2-4ac是一元二次方程的一个重要知识点，其显性应用不言而喻.值得关注的是，有些非一元二次方程的问题，正面求解比较困难，但细究问题实质，却与一元二次方程有关联，通过转化、构造与之相关的一元二次方程，再借助根的判别式促成问题的解决，此方法简明精巧，功能独特，体现了其隐形应用价值，本文采撷几道中考压轴题，剖析解法，以飨读者.

例1（2012年山东临沂）已知，在矩形ABCD中，AB=a，BC=b，动点M从点A出发沿边AD向点D运动.

（1）如图1，当b=2a，点M运动到边AD的中点时，请证明∠BMC=90°.

（2）如图2，当b＞2a时，点M在运动的过程中，是否存在∠BMC=90°，若存在，请给出证明；若不存在，请说明理由.

（3）如图3，当b＜2a时，（2）中的结论是否仍然成立？请说明理由.

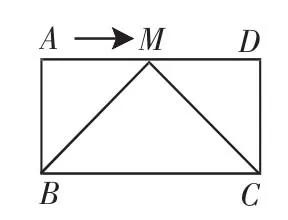
图1

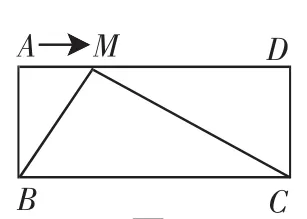
图2

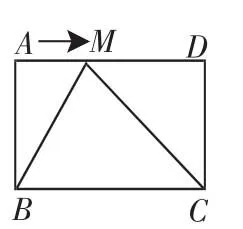
图3

解：（1）略.

（2）存在，理由如下.

若∠BMC=90°，则∠AMB=∠BMC=90°.

又因为∠AMB+∠ABM=90°，所以∠ABM=∠DMC.

又因为∠A=∠D=90°，所以△ABM∽△DMC.

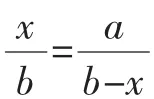
因为b＞2a，a＞0，b＞0，所以Δ=b2-4a2＞0，

所以方程有两个不相等的实数根.

又因为两根之积等于a2＞0，所以两根同号.

又因为两根之和等于b＞0，所以两根为正，符合题意.

所以当b＞2a时，存在∠BMC=90°.

（3）不成立，理由如下.

若∠BMC=90°，由（2）可知x2-bx+a2=0.

因为b＜2a，a＞0，b＞0，所以Δ=b2-4a2＜0，所以方程没有实数根.

所以当b＜2a时，不存在∠BMC=90°，即（2）中的结论不成立.

评注：第（2）小题探究是否存在点M，使∠BMC=90°，关键是设AM=x，根据相似三角形的对应边成比例，可得方程x2-bx+a2=0，由b＞2a，a＞0，b＞0，即可判定Δ=b2-4a2＞0，从而确定结果，第（3）小题也随之获解.

例2 （2012年湖北宜昌）如图4，在直角梯形ABCD中，AD∥BC，∠ABC=90°.点E为底边AD上一点，将△ABE沿直线BE折叠，点A落在梯形对角线BD上的点G处，EG的延长线交直线BC于点F.

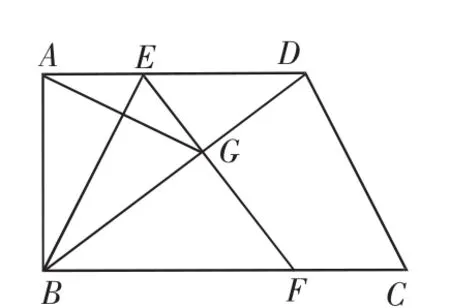
图4

（1）点E可以是AD的中点吗？为什么？

（2）求证：△ABG∽△BFE.

（3）设AD=a，AB=b，BC=c.

①当四边形EFCD为平行四边形时，求a，b，c应满足的关系；

②在①的条件下，当b=2时，a的值是唯一的，求∠C的度数.

解：（1）、（2）略.

（3）①因为四边形EFCD为平行四边形，

所以EF∥DC.

因为由折叠知，∠DAB=∠EGB=90°，

所以∠DAB=∠BDC=90°.

又因为AD∥BC，所以∠ADB=∠DBC，

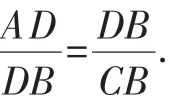
②由①和b=2得关于a的一元二次方程a2-ac+4=0.

由题意，a的值是唯一的，即方程有两相等的实数根，所以Δ=0，即c2-16=0.

因为c＞0，所以c=4.由a2-4a+4=0，得a=2.

由①△ABD∽△DCB和a=b=2，得△ABD和△DCB都是等腰直角三角形，所以∠C=45°.

评注：第②小题把b=2代入①所得a2+b2=ac，构造出关于a的一元二次方程a2-ac+4=0，根据a是唯一的，可以利用Δ=c2-16=0，求出c=4，再代入方程求出a=2，然后由①△ABD∽△DCB和a=b=2，得△ABD和△DCB都是等腰直角三角形，求得∠C=45°.

例3（2012年湖北十堰）抛物线y=-x2+bx+c经过点A、B、C，已知A（-1，0），C（0，3）.

（1）求抛物线的解析式；

（2）如图5，P为线段BC上一点，过点P作y轴的平行线，交抛物线于点D，当△BDC的面积最大时，求点P的坐标；

（3）如图6，抛物线的顶点为E，EF⊥x轴于F点，M（m，0）是x轴上一动点，N是线段EF上一点，若∠MNC=90°，请求出实数m的变化范围，并说明理由.

图5

图6

解：（1）抛物线解析式为y=-x2+2x+3.（2）略.

（3）由（1）得y=-x2+2x+3=-（x-1）2+4，所以E（1，4），所以OF=1，EF=4，OC=3.

过C作CH⊥EF于H点，则CH=EH=1.

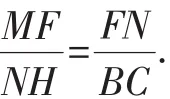
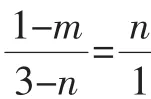
因为关于n的方程有解，所以Δ=（-3）2-4（-m+1）≥0，

当M在EF右侧时，如图8，在Rt△CHE中，CH=EH=1，∠CEH=45°，即∠CEF=45°.

作EM⊥CE交x轴于点M，则∠FEM=45°.

因为FM=EF=4，所以OM=5，即N为点E时，OM=5，所以m≤5.

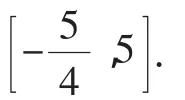
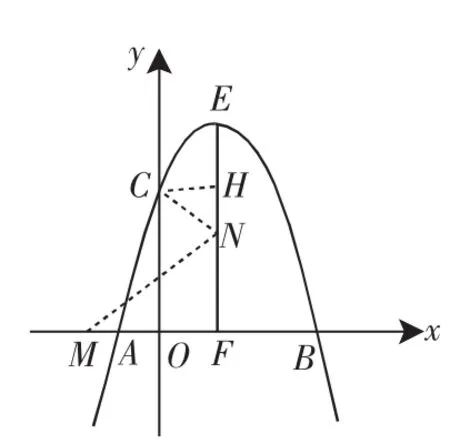
图7

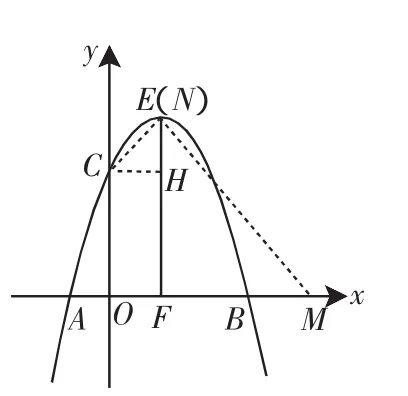
图8

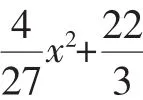
（1）求直线y=kx的解析式和线段OA的长度.

（2）点P为抛物线第一象限内的动点，过点P作直线PM，交x轴于点M（点M、O不重合），交直线OA于点Q，再过点Q作直线PM的垂线，交y轴于点N.试探究：线段QM与线段QN的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由.

（3）如图10，若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点O、A不重合），点D（m，0）是x轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD.继续探究：m在什么范围时，符合条件的E点的个数分别是1个、2个？

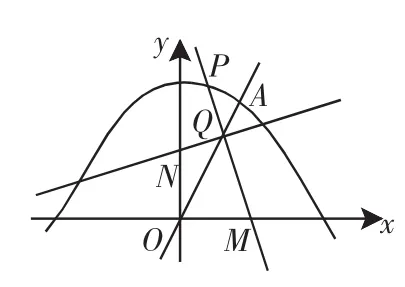
图9

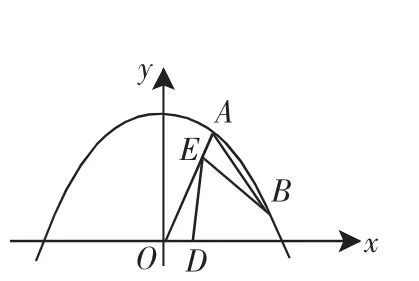
图10

（3）延长AB交x轴于点F，过点A作AR⊥x轴于点R.

如图11，因为∠AOD=∠BAE，所以AF=OF.设F（x，0），

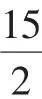
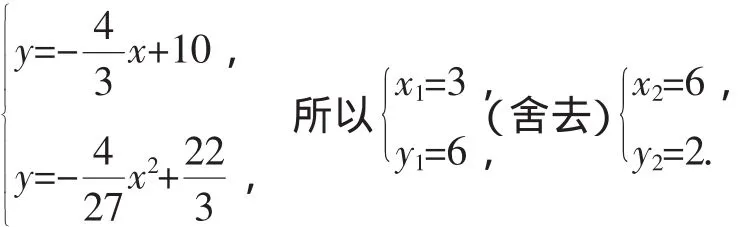
所以B（6，2），所以AB=5.

在△ABE与△OED中，因为∠BAE=∠BED，所以∠ABE+∠AEB=∠DEO+∠AEB，所以∠ABE=∠DEO.

因为∠BAE=∠EOD，所以△ABE∽△OED.

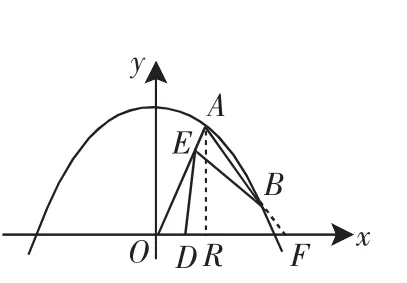
图11

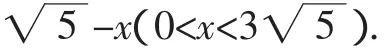
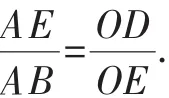
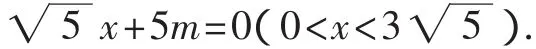
因为△=45-20m≥0，