基于改进粒子群算法的跨组织资源链构建研究

王正成 咸 达

浙江理工大学，杭州，310018

0 引言

跨组织的制造资源集成共享与优化配置能有效解决组织间资源占有不平衡、组织资源重复投资等问题，并成为提升制造企业核心竞争力的关键。当前多数跨组织协同制造中的资源集成共享研究侧重于产品形成过程中单个或部分环节上的资源集成共享，未能在全局上实现资源的优化配置，且聚焦于跨组织协同制造中资源集成共享的个别或部分独立问题的解决，未能形成系统性的综合解决方案，最终使得跨组织协同制造中资源集成共享的效率与效果不佳。另外在跨组织制造资源集成共享与优化配置的过程中，如何使各个制造任务在时间、成本、服务、质量等准则下实现全局优化配置，并构建跨组织制造资源链是制造企业的关键问题之一，该问题是动态模糊多目标决策NP问题，当前大多数文献从不同的角度对该问题进行求解。如Sawik［1］研究了在供应商选择和订单分配的协同制造环境下，考虑供应链中断和延迟的风险，通过该场景分析提出一种混合整数规划的方法，以合并风险。齐二石等［2］研究了复杂零件协同制造的资源优化配置问题，以加工时间、运输费用和加工质量为目标建立数学模型，并利用遗传算法求解。Vanteddu［3］根据供应商选择问题，主要考虑了库存成本和周期时间，并将一个“逆反应系数”加入到该问题模型中。孙忠良等［4］针对制造资源配置评价问题，建立了成本收益数据包络分析数学模型，并提出了资源的优化配置策略。董景峰等［5］以质量、成本、交货期和交货提前期为评估指标，建立了数学模型并利用蚁群算法求解此问题。苏世彬等［6］针对动态联盟先进制造模式，结合知识管理和模拟退火算法的思路对动态联盟盟员进行选择与淘汰。在实际的跨组织资源链的构建过程中，考虑的因素复杂多样，每个企业的生产能力、服务能力、管理能力、产品质量等不同，在选择的过程中就会导致最优的全局配置不同，而且在求解模型问题的方法上，容易陷入局部最优值且存在收敛速度慢等问题，难以解决大规模全局优化问题。

1 研究思路

本文提出了跨组织资源链概念以及通过该资源链的构建实现跨组织协同制造中资源集成共享与优化配置的思路，如图1所示。

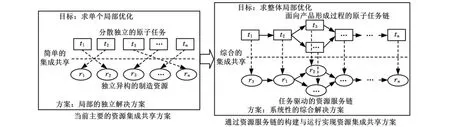
图1 通过资源服务链构建与运行实现资源集成共享

2 数学模型

跨组织制造资源链首先根据产品形成过程分解协同制造总任务，形成时序与约束关联的一系列原子任务链，在此基础上原子任务链驱动制造资源需求形成由跨地域的资源组成的动态、复杂和基于时序的有向网络图，如图2所示。

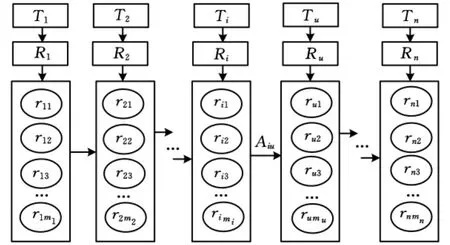
图2 跨组织资源链有向网络结构示意图

该问题可以形式化描述为：L＝ ｛T，R，rij，Aiu｝（i＝1，2，…，n；j＝1，2，…，mi）。T为某制造企业接到订单所形成的协同制造总任务，T＝｛T1，T2，…，Tn｝，n为协同制造总任务经分解形成的原子任务数量，mi为某一原子任务Ti的候选资源服务数量。R为候选资源集合，R＝｛R1，R2，…，Rn｝，T1→R1表示为原子任务T1经检索匹配和选择评价形成满足其时序约束需求的候选资源集R1。候选资源rij表示第i个原子任务选择第j个候选资源服务来完成。Aiu＝ ｛Ciu，Tiu｝表示两个前后有直接关系的原子任务之间的连接，包含连接成本Ciu和连接时间Tiu。

基于上述考虑，把跨组织资源链构建问题转化为时序约束限制的路径寻优问题。在实际的跨组织协同制造中，影响跨组织资源服务链构建的因素很多，如时间、成本、服务能力、质量、生产能力、环境、信誉等，这些因素都会影响全局最优的跨组织制造服务链的构建。由于企业间竞争激烈，内外部环境变化迅速，因此建立一个综合各种因素的复杂数学模型并进行求解非常困难，也无现实必要性。为此本文不失一般性地将问题抽象化，把协同制造组织最为关注的时间、成本、服务能力作为服务链构建的评价指标，由此定义跨组织资源服务链的数学模型如下。

定义决策变量：

跨组织协同制造的时间构成主要是各个原子任务生产制造时间和各个时序原子任务之间的协调连接时间，因此定义时间目标函数为

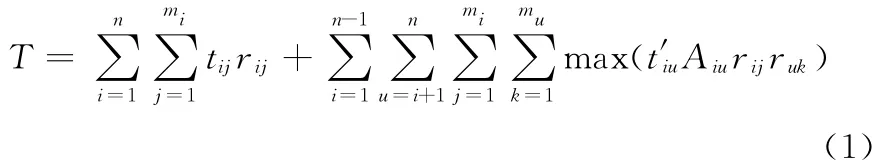
其中，tij表示第i个原子任务在第j个候选资源服务所进行的生产制造时间，t′iu表示从原子任务i转移到原子任务u的连接时间。将跨组织协同制造任务链中每个并行任务转移到下一任务所需要时间的最大值进行累加，符合现实生活对跨组织协同制造过程时间的构成。

同样地，跨组织协同制造资源服务链的制造成本是由原子任务生产制造成本和各个原子任务之间的连接成本组成的。定义成本目标函数为

其中，cij表示第i个原子任务在第j个候选企业所进行的生产制造成本，diu表示从原子任务i转移到原子任务u所需的成本，类似于现实生活中的运输成本。

由于当前候选资源的服务能力frij为效用性指标，而时间、成本都属于定量指标，因此有必要对服务能力指标进行量纲一修正［7］，可采用：fij＝ （frij－fmin）/（fmax－fmin）进行修正。其中fmax、fmin分别表示服务能力指标的最大值和最小值。定义服务能力目标函数为

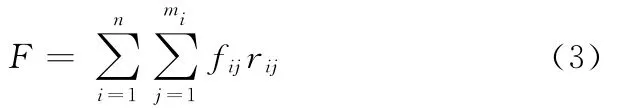
很明显这是一个多目标优化函数的问题，为此引入权重μ，对目标函数进行优化处理：

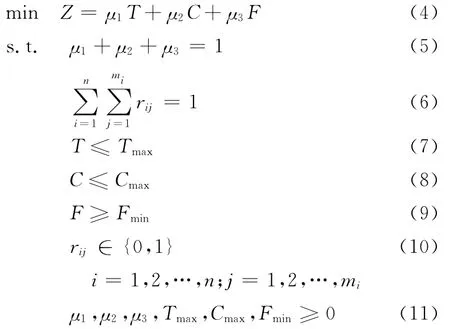
式中，μ1、μ2、μ3分别为时间T、成本C、服务能力F所占的权重比例；Tmax、Cmax分别为完成整个服务链所需要的时间和成本的最大值；Fmin为服务链中所选择的候选企业综合服务能力的最小值。

为了求解该模型，本文采用Michalewicz等［8］提出的一种罚函数法解除约束，其表达式为

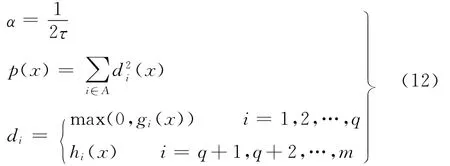
式中，A为起作用的约束集，由所有等式约束和不能满足的不等式约束组成；α为惩罚因子；p（x）为罚函数；τ为可变惩罚因子；gi（x）为不等式约束；hi（x）为等式约束；q为不等式约束个数；m为条件约束个数。

化简后的无约束方程的表达式为

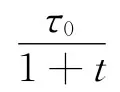
由式（13）可知，在迭代初期，对不可行解惩罚较小，需扩大可行解的搜索，避免陷入局部最优解；后期惩罚力度变大，需限定搜索区域，利于快速寻找全局最优解。

3 构建算法

3.1 二进制粒子群优化算法

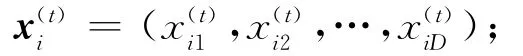
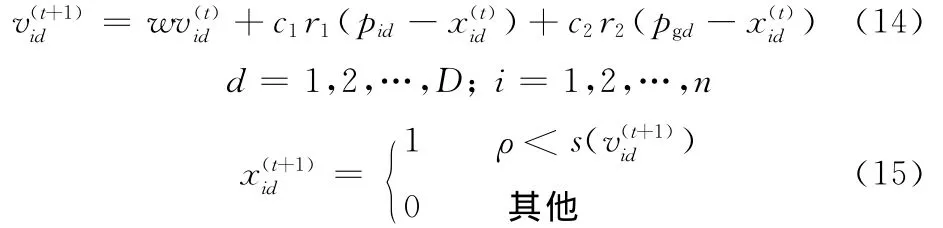
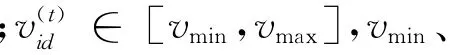
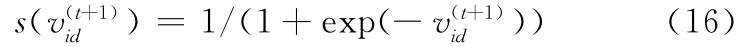
3.2 改进的粒子群优化算法

3.2.1 粒子位置编码

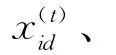
例如，有4个原子任务，原子任务1有2个候选企业，原子任务2有3个候选企业，原子任务3有4个候选企业，原子任务4有2个候选企业，其中原子任务1选择了第1个候选企业，原子任务2选择了第3个候选企业，原子任务3选择了第2个候选企业，原子任务4选择了第1个候选企业，则粒子的编码位置如图3所示。此时粒子的编码位置x＝ ｛1 0 0 0 1 0 1 0 0 1 0｝。

图3 粒子位置编码构造图

3.2.2 粒子的参数设置

粒子i在D维空间进行搜索，相当于粒子在所有的候选企业中搜索最优的解，在BPSO算法中，惯性权重w决定了粒子先前速度对当前速度的影响程度，直接关系到BPSO算法的搜索能力与收敛速度。当惯性权重较大时，有利于全局搜索，且收敛速度快，但不易得到精确解；当惯性权重较小时，有利于局部搜索，但容易陷入局部最优解。本文参照文献［10］对w采用线性递减策略，公式为

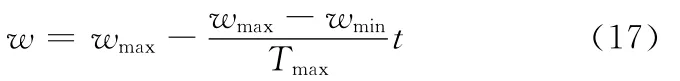
其中，wmax、wmin分别为惯性权重的最大值和最小值，Tmax为最大迭代次数，t为当前迭代次数。将粒子的初始速度设为

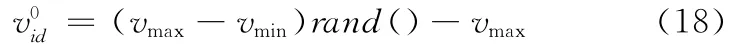
这样在迭代开始时，可以很快地进行全局搜索，定位最优解的大致位置，随着w的减小，粒子速度减小，开始进行局部搜索，寻找最精确的最优解。

如果粒子的速度超出vmax，可能会使粒子飞过最优解；若粒子的速度太小，则导致粒子收敛速度过小，可能被局部最优解所吸引，无法找到最优解，因此对［vmin，vmax］范围外的粒子速度进行修正：

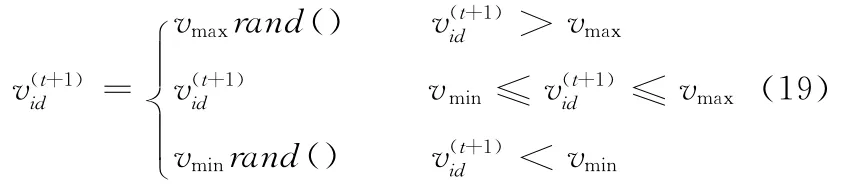
3.2.3 粒子的位置更新

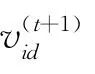
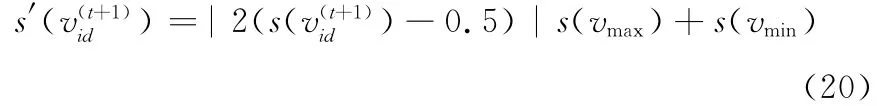
将式（20）进行归一化处理：

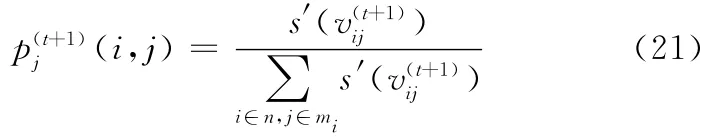
位置的更新公式如下：

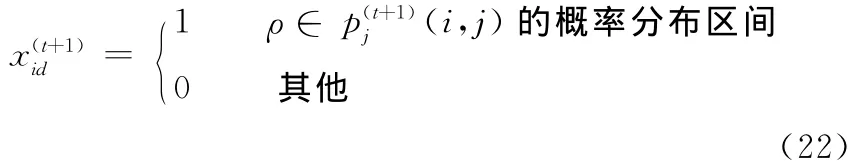
其中，ρ为［0，1］之间的随机数。例如跨组织资源链中原子任务1的候选企业有3个，归一化后的概率分别为0.35、0.25、0.40，产生的随机数为0.72，由于0.72在（0.6，1）之间，因此原子任务1应选择候选企业3，并将候选企业3的位置x13设置为1，x11、x12设置为0。

3.2.4 算法实现

利用改进的粒子群算法求解该模型的伪代码如下：

4 算例仿真

本文假设有一跨组织协同制造链（图4），有5个原子任务，每个原子任务的候选企业个数和每个候选企业的生产制造的时间（单位为天）、成本（单位为千元）、服务能力参数如表1所示，各个原子任务之间的连接成本、时间参数等如表2～表4所示。其中Rij表示原子任务i选择第j个候选企业。

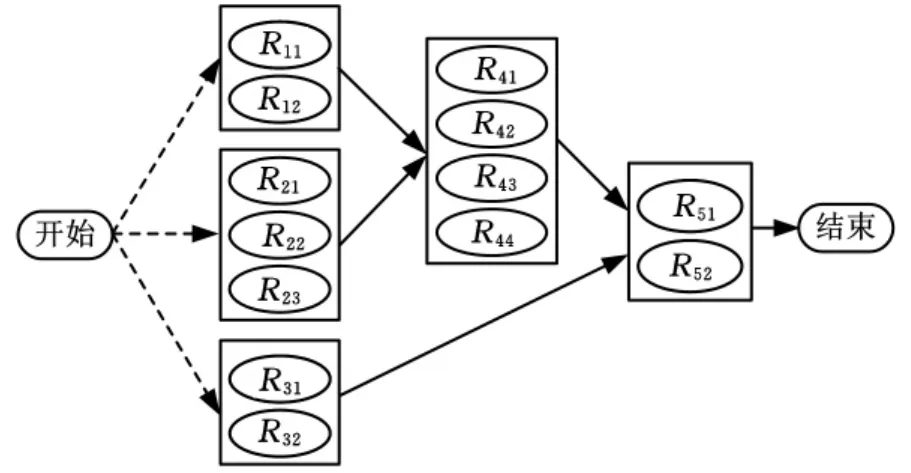
图4 仿真算例跨组织协同制造链网络拓扑结构示意图

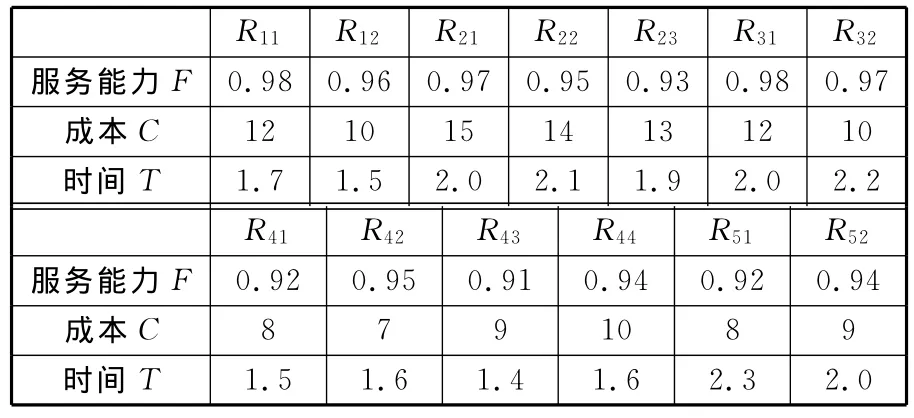
表1 候选企业的服务能力、成本、时间参数表

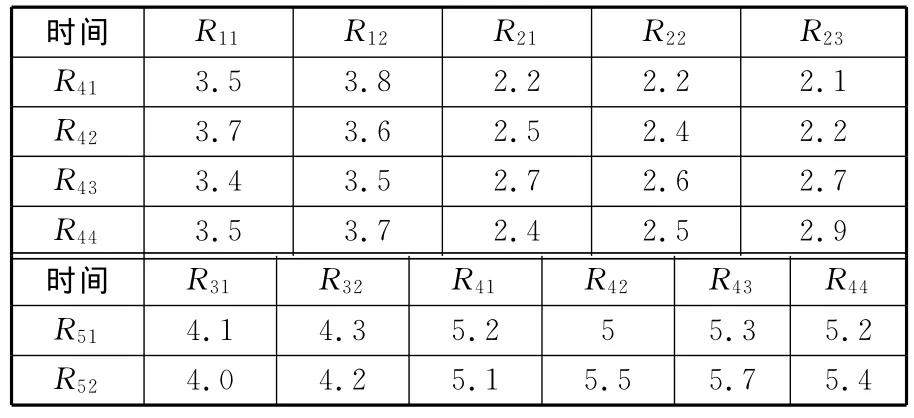
表2 具有时序性的候选企业的连接时间

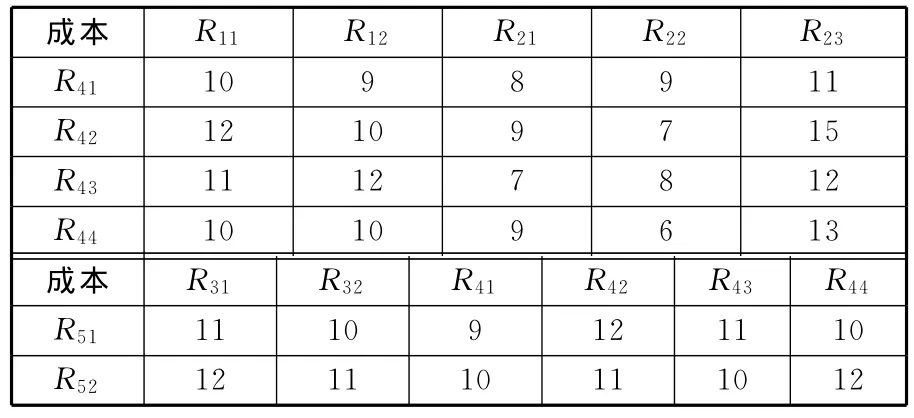
表3 具有时序性的候选企业的连接成本

表4 服务链中最后转移到目的地的参数表

最后通过MATLAB平台进行仿真计算，其中设Cmax＝100千元；Tmax＝23d；Fmin＝4.5；采用改进的粒子群算法（CPSO）进行计算，粒子数为30，迭代次数为200，学习因子c1＝c2＝1.494 45，wmax＝0.9，wmin＝0.4；vmax＝6，vmin＝－6；跨组织协同制造链中评价指标的权重可根据具体问题进行相应的分析，如μ3＝0，则该模型就是基于时间和成本考虑的服务链模型，这里可令μ1＝0.3，μ2＝0.3，μ3＝0.4。最后求解的结果为minZ＝37.476，其中成本为97千元，完成任务所需时间为21.6d，服务能力为4.74。此时粒子的最优位置x＝｛0 1 1 0 0 0 1 1 0 0 0 1 0｝，构建的跨组织协同制造服务链如图5所示。在求解该跨组织协同制造服务链时将改进后的粒子群算法与标准的粒子群算法相比较，如图6所示，可以看到BPSO陷入局部最优值，并且收敛速度较慢，而改进后的粒子群算法收敛速度较快，到达最优值的迭代次数少，该结果表明改进后的粒子群算法能够获得最优值并具有非常快的收敛速度。

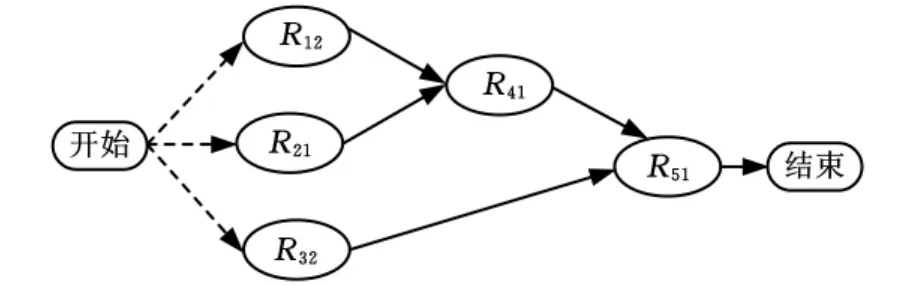
图5 最优的跨组织资源服务链构造图

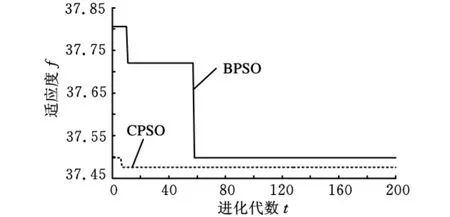
图6 算法仿真比较示意图

5 结束语

本文通过对跨组织协同制造资源服务链的研究，构建了以时间、成本和服务能力为评价指标体系的数学模型，通过罚函数法将约束问题转变成无约束优化问题，并利用改进的粒子群算法进行求解，提出了粒子的编码方法，并对粒子的速度进行处理，归一化后的概率可以决定粒子的位置，直接对候选资源的选择进行判定。该算法具有收敛速度快、全局优化能力强、不易陷入局部最优的优点。最后通过仿真算例验证了算法的高效性，为解决跨组织协同制造资源服务链的研究问题提供了一种切实可行的方法。

［1］Sawik T.Selection of a Dynamic Supply Portfolio in Make－to－order Environment with Risks［J］.Computers and Operations Research，2011，4（38）：782－796.

［2］齐二石，李辉，刘亮.基于遗传算法的虚拟企业协同资源优化问题研究［J］.中国管理科学，2011，19（1）：77－83.

Qi Ershi，Li Hui，Liu liang.Research on Collaborative Resource Optimization of Virtual Enterprises Based on Genetic Algorithm［J］.Chinese Journal of Management Science，2011，19（1）：77－83.

［3］Vanteddu G.Supply Chain Focus Dependent Supplier Selection Problem［J］.International Journal of Production Economics，2011，129（1）：204－216.

［4］孙忠良，吴文武，洪军，等.基于数据包络分析的网络化制造联盟企业制造资源配置评价研究［J］.计算机集成制造系统，2008，14（5）：962－969.

Sun Zhongliang，Wu Wenwu，Hong Jun，et al.Resource Allocation Evaluation of Networked Manufacturing Extended Enterprise Based on DEA［J］.Computer Integrated Manufacturing Systems，2008，14（5）：962－969.

［5］董景峰，王刚，吕民，等.基于改进蚁群算法的多供应商选择问题求解［J］.计算机集成制造系统，2007，13（8）：1639－1644.

Dong Jingfeng， Wang Gang，Lü Min，et al.Multi－supplier Selection Problem Solution Based on Improved Ant Colony Algorithm［J］.Computer Integrated Manufacturing Systems，2007，13（8）：1639－1644.

［6］苏世彬，黄瑞华.基于模拟退火算法的动态联盟盟员的动态选择［J］.中国管理科学，2005，13（1）：90－94.

Su Shibin，Huang Ruihua.Members Dynamic Selection Based on Simulated Annealing Algorithm in Virtual Enterprise［J］.Chinese Journal of Management Science，2005，13（1）：90－94.

［7］王正成，谢先文.基于FAHP和改进蚁群算法的网络化制造资源链构建研究［J］.中国机械工程，2012，23（12）：1487－1492.

Wang Zhengcheng，Xie Xianwen.Resource Service Chain Construction for Networked Manufacturing Based on FAHP and Improved Ant Colony Algorithm［J］.China Mechanical Engineering，2012，23（12）：1487－1492.

［8］Michalewicz Z，Schoenauer M.Evolutionary Algorithms for Constrained Parameter Optimization Problems［J］.Evolutionary Computation Journal，2010，4（1）：1－32.

［9］Kennedy J，Eberhart R C.A Discrete Binary Version of the Particle Swarm Algorithm［C］//Proceeding of the World Multiconference on Systemics，Cybernetics and Informatics.Piscataway：IEEE Service Center，1997：4104－4109.

［10］王正成，潘晓弘，潘旭伟.基于蚁群算法的网络化制造资源服务链构建［J］.计算机集成制造系统，2010，16（1）：174－181.

Wang Zhengcheng，Pan Xiaohong，Pan Xuwei.Resource Service Chain Construction for Networked Manufacturing Based on Ant Colony Algorithm［J］.Computer Integrated Manufacturing Systems，2010，16（1）：174－181.