磨削参数对ELID内圆磨削轴承外圈的影响

李秦峰 任成祖 张开飞

天津大学天津市先进制造技术与装备重点实验室，天津，300072

0 引言

作为一个精密的机械元件，滚动轴承的振动和噪声与整个机械系统的性能有直接的关系，其中轴承外圈沟道的波纹度是影响轴承振动和噪声的一个主要因素。波纹度的产生很大程度上是由磨削过程中机床所受到的振动干扰造成的［1］。在传统的轴承工业中，套圈内表面经常采用研磨和抛光工艺来满足精度要求，然而这些方法将增加设备投资且延长加工时间［2］。在线电解修整（ELID）磨削技术是近几年来金属结合剂超硬磨料修整技术的一项新成就，具有加工精度高、效率高以及适应加工材料范围广等特点，被广泛应用于各种金属和非金属材料的磨削加工中［3］。更重要的是，这项技术被成功地应用到内圆表面的超精密加工中，能够很好地解决内圆磨削中由于磨削条件差而导致的砂轮极易阻塞等问题［4－6］。然而，在ELID内圆磨削方式下，很少有学者研究磨削深度和砂轮进给速度这两个磨削参数对磨削质量的影响，并且也很少有人分析和比较这两个参数对磨削过程影响的程度。因此，本文在大量试验的基础上，研究了磨削深度和砂轮进给速度对材料去除率以及磨削后表面波纹度的影响，从氧化膜状态、振动功率以及材料去除机理等方面进行了理论分析，并根据试验结果提出了实际ELID内圆磨削中磨削参数的选择建议。

1 试验设备及方法

图1 试验系统示意图

本试验建立在数控改造后进给精度为1μm的磨床上。如图1所示，连接ELID脉冲电源正极的铸铁基CBN砂轮安装在机床的水平轴上。轴承外圈安装在电磁无心夹具上，在ELID磨削过程中，轴承外圈通过碳刷与脉冲电源的负极相连。磨削过程中的振动信号由安装在电磁无心夹具绝缘支撑上的加速度传感器获取，输出范围为±5V的电压信号，修整电流由霍尔电流传感器测量得到。上述两个实时信号均通过采集卡采集，并在工控机中显示和记录。试验装置及设备见图2及表1。

图2 试验系统实物图

表1 试验设备及条件

工件表面波纹度产生的原因很多，其中最主要的原因是磨削过程中的振动。本文所研究的波纹度的范围为每圈50至150个波［7］，并且试验过程的工件转速固定在2r/s，因此在本试验中，最有可能导致波纹度产生的振动干扰信号的频率范围为100～300 Hz［8］。磨削过程采集得到的振动信号经过100～300Hz频率范围的滤波后，采用下式可计算得到平均振动功率W：

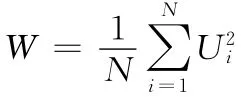
式中，N为振动信号采样点的总个数；U为代表振动信号的电压值。

2 试验结果及讨论

2.1 单因素试验条件下的磨削深度和砂轮进给速度对ELID内圆磨削的影响

在超精密磨削的常用加工参数范围内［3－4］，工件转速和砂轮进给速度分别设定为120r/min和50mm/min保持不变，在工件上做磨削深度分别为1μm、2μm、3μm 和4μm 的普通内圆磨削和ELID内圆磨削试验。每组试验重复三次以减小误差。图3所示为对应于普通磨削和ELID磨削方式下，采用不同的磨削深度得到的振动功率，可以明显看出，在两种磨削方式下，振动功率均随着磨削深度的增大而增大，但是ELID内圆磨削时的振动功率较小。图4所示为两种磨削方式下采用不同磨削深度加工得到的波纹度。从试验结果可以看出，在超精密磨削参数范围内，磨削深度对ELID内圆磨削与普通内圆磨削的影响规律基本一致，只是当磨削深度小于或等于3μm时，ELID磨削得到的波纹度明显优于普通磨削，当磨削深度为4μm时，由于砂轮表面氧化膜磨损严重，导致两种磨削方式下波纹度相差不大。上述试验结果表明，不论是ELID内圆磨削还是普通内圆磨削，随着磨削深度的增大，波纹度都不断增大，但ELID磨削得到的波纹度较小。

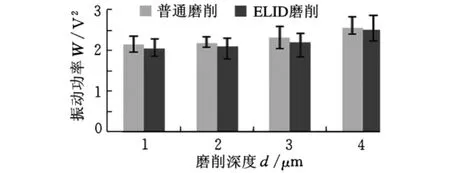
图3 磨削深度对磨削过程中振动功率的影响

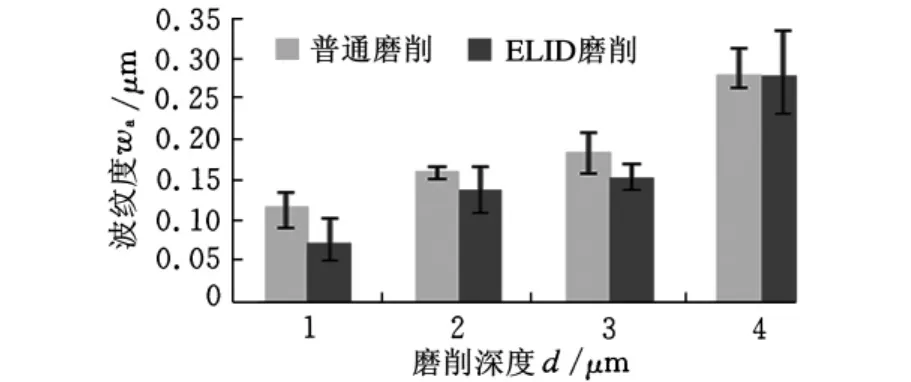
图4 磨削深度对表面波纹度的影响

同样在超精密磨削的参数范围内，工件转速和磨削深度分别设定为120r/min和1μm不变，在工件上做砂轮进给速度为50mm/min、100mm/min、150mm/min和200mm/min的磨削试验，每组试验重复三次。由图5可以看出，在普通磨削和ELID磨削两种内圆磨削方式下，磨削过程中的振动功率随砂轮进给速度增大而不断增大。图6所示为采用不同砂轮进给速度得到的工件表面波纹度，可以看出，虽然两种磨削方式下波纹度均是随着砂轮进给速度增大而增大的，但相对于普通内圆磨削来说，ELID磨削得到的波纹度随着磨削深度增大而增大的幅度较小，并且最终得到的波纹度也大于普通磨削。

从试验结果可以看出，随着磨削深度或砂轮进给速度的增大，波纹度的增大趋势与振动功率的增大趋势非常相似，即磨削过程中的振动信号在一定程度上能够预测加工后工件表面波纹度的大小。图7为简化的砂轮与工件相互作用系统原理图，假设磨削时振动信号为V，则有

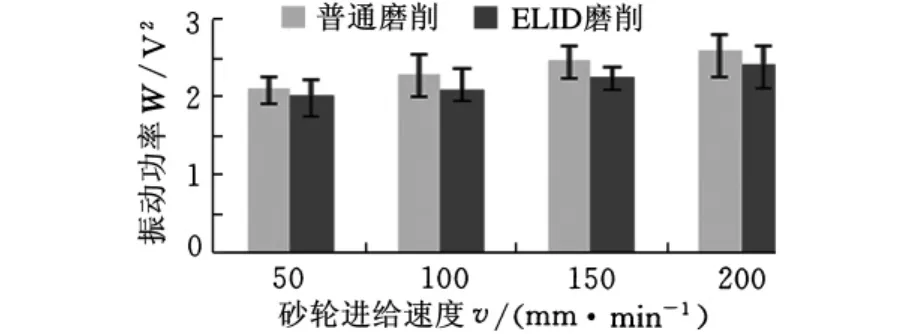
图5 砂轮进给速度对磨削过程中振动功率的影响

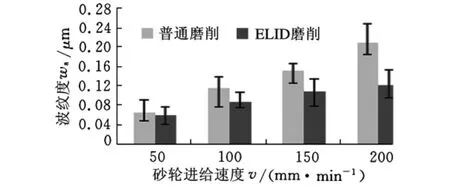
图6 砂轮进给速度对表面波纹度的影响

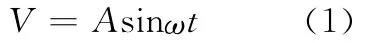
式中，A为振动幅值；ω为振动频率。

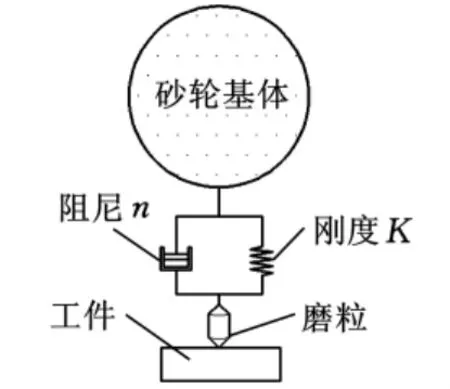
图7 砂轮与工件相互作用原理图

在此振动干扰的作用下，砂轮与工件表面产生相对位移y，即工件表面形成的波纹度幅值。可以将砂轮系统简化为一个二阶系统：

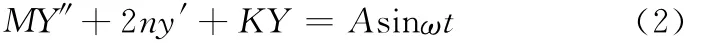
式中，M为砂轮系统质量；n为砂轮系统阻尼系数；K为砂轮系统刚度。

则可得到式（2）稳态解的波纹度幅值Y为

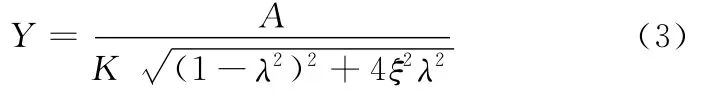
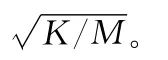
由式（3）可以看出，工件表面产生的波纹度幅值Y与砂轮系统的阻尼比ξ成反比，由于ELID磨削时砂轮表面形成了一层富有弹性的氧化膜，其阻尼系数远大于普通磨削时砂轮与工件直接接触的情况，因此，ELID磨削能够得到较好的表面波纹度。并且式（3）中工件表面波纹度幅值Y与振动干扰的幅值A成正比，进而从理论上解释了根据磨削过程中振动的大小能够有效预测工件表面波纹度的大小。

2.2 不同磨削参数组合下的ELID磨削表现

之前的单因素试验充分说明了在ELID内圆磨削中，随着磨削深度或砂轮进给速度的增大，表面波纹度均不断变差。但是磨削过程是建立在这两个参数共同作用的基础上的，两者对工件表面质量的影响程度也是有区别的，因此有必要研究实际ELID内圆磨削过程中这两个参数究竟是谁起到支配性作用。

试验步骤如下：在常用的超精密磨削参数范围内，砂轮转速设为30 000 r/min，工件转速为120r/min，占空比为50%，电源电压为60V。在不改变其他参数的情况下，分别在轴承外圈内表面上进行三组不同磨削参数组合的试验，第一组采用1μm的磨削深度和200mm/min的砂轮进给速度；第二组采用2μm的磨削深度和100 mm/min的砂轮进给速度；第三组采用4μm的磨削深度和50mm/min的砂轮进给速度。在这三组试验中，磨削深度不断增大而砂轮进给速度不断减小，并且保证三组磨削参数的理论材料去除率相同。每组试验重复三次且每次磨削前保证磨削条件和状态相同。

图8所示为不同磨削参数组合下的修整电流，可以看出三组试验中的修整电流的修整频率不断增大，并且修整电流也不断变大，其中第三组试验中的修整电流最大时已经接近0.3A，远远超过第一组和第二组的电流大小。图9所示为对应三组不同磨削参数组合得到的平均振动功率，可以看出，振动功率值不断增大。图10所示为对应于不同磨削参数组合的波纹度，可以看出，波纹度不断增大。图11显示了三组试验后轴承工件的实际材料去除量，其变化趋势与波纹度的变化趋势一致，也是逐渐增大。

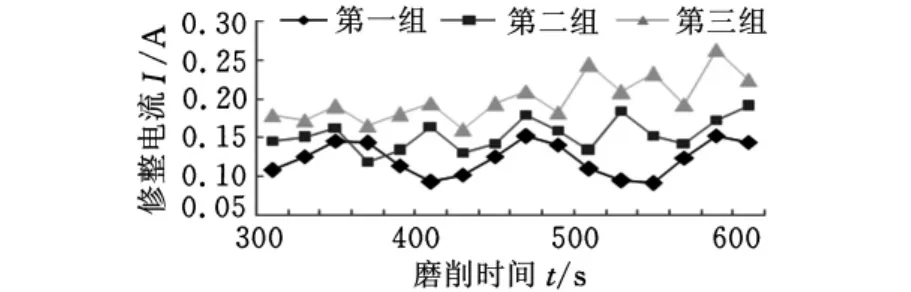
图8 三组磨削参数组合下的修整电流

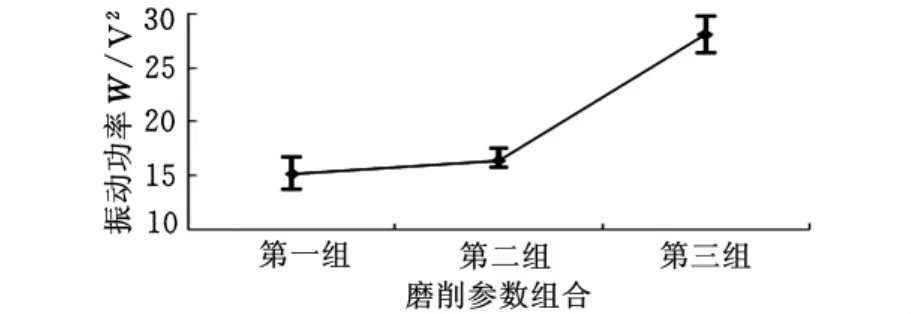
图9 三组磨削参数组合下的振动功率

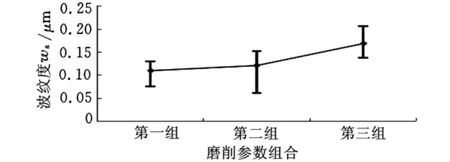
图10 三组磨削参数组合下的波纹度

图11 三组磨削参数组合下的材料去除量

根据之前单因素试验的结果，增大磨削深度或砂轮进给速度均会使波纹度增大，即减小磨削深度或砂轮进给速度均会使波纹度减小。但是，上述三组磨削参数组合的试验研究表明，波纹度及材料去除率均随着磨削深度增大而增大，并不随砂轮进给速度减小而减小。明显可以得出在常用的超精密内圆磨削的参数范围内，磨削深度对ELID内圆磨削有着更重要的影响的结论。

ELID磨削过程中的在线电解修整作用在砂轮表面形成了一层氧化膜，该氧化膜存在于金属结合剂基体与被磨削工件之间，可以容纳、承托一定数量的因电解而脱落的磨料，使氧化膜成为一种含有微细磨料并具有良好柔韧性的研磨膜，因此ELID磨削的材料去除实际上是一种磨、研、抛相结合的复合加工方式，而氧化膜的状态决定了材料的主要去除方式。当采用较大的砂轮进给速度和较小的磨削深度的参数组合时，修整电流和振动功率均保持在一个较低的水平，这也意味着砂轮表面氧化膜的磨损程度比较低，砂轮表面不断电解生成的新氧化膜能够充分修补已经磨损掉的氧化膜，并使其维持在一个比较厚的状态。并且当氧化膜的厚度达到一定程度时，使得参与磨削的磨粒大部分甚至全部处于氧化膜的包裹之中，此时ELID磨削的材料去除主要是以微细超硬的磨粒对工件表面研磨抛光的方式进行的，从而获得较高的表面质量和较低的材料去除率。当磨削试验采用较小的砂轮进给速度和较大的磨削深度时，修整电流较大，同时振动功率也显著增大，表明氧化膜磨损剧烈并变得很薄，已经不能在磨削过程中很好地起到对振动干扰的阻尼作用，并且此时参与磨削的磨粒大部分都由氧化膜下层较硬的金属结合剂把持。此时砂轮的主要材料去除方式是微细超硬磨料的微量磨削，研磨抛光作用并不占主导地位，因此最终得到较差的表面质量和较高的材料去除率。

综上所述，在实际的ELID磨削过程中，可以先采用较大的磨削深度来实现较高的材料去除率，以消除上道工序中的加工痕迹和变质层，加工一段时间后再采用较小的磨削深度，最终实现对工件表面的研磨抛光并获得较好的表面质量。

3 结论

（1）ELID磨削过程中的振动功率相对于普通磨削较小。

（2）磨削过程中振动信号的大小能够有效地预测磨削后工件表面的波纹度。

（3）在ELID内圆磨削条件下，磨削深度和砂轮进给速度的增大均会引起波纹度变大，但磨削深度要比砂轮进给速度对磨削表面波纹度以及材料去除的影响更显著。

［1］Inasaki I，Karpuschewski B，Lee H S.Grinding Chatter－ Origin and Suppression ［J］.CIRP Annals－Manufacturing Technology，2001，50（2）：515－534.

［2］夏新涛，马伟.滚动轴承制造工艺学［M］.北京：机械工业出版社，2007.

［3］Ohmori H，Nakagawa T.Mirror Surface Grinding of Silicon Wafers with Electrolytic In－process Dressing［J］.Annals of the CIRP，1990，39（1）：329－332.

［4］Qian Jun，Li Wei，Ohmori H.Precision Internal Grinding with a Metal－bonded Diamond Grinding Wheel［J］.Journal of Materials Processing Technology，2000，105（1/2）：80－86.

［5］Qian Jun，Ohmoria H，Lin Weimin.Internal Mirror Grinding with a Metal/Metal－Resin Bonded Abrasive Wheel［J］.International Journal of Machine Tools ＆ Manufacture，2001，41：193－208.

［6］杨黎健，任成祖，靳新民.轴承套圈内圆ELID磨削试验［J］.中国机械工程，2011，22（2）：212－214.

Yang Lijian，Ren Chengzu，Jin Xinmin.Internal Cylindrical ELID Grinding Experiment of Bearing Rings［J］.China Mechanical Engineering，2011，22（2）：212－214.

［7］全国滚动轴承标准化技术委员会.滚动轴承零件圆度和波纹度误差测量及评定方法［S］.北京：中国标准出版社，2004.

［8］马伏波.表面波纹度的研究［J］.煤矿机械，2008，29（10）：89－90.

Ma Fubo.Study of Surface Waveness［J］.Coal Mine Machinery，2008，29（10）：89－90.