环状可展机构运动学分析方法及应用研究

韩莹莹 袁 茹 郑钰祺

西北工业大学，西安，710072

0 引言

可展机构具有展开后面积大、收拢时占用空间小且便于收放和运输等特点，在航天、航空、建筑等领域的应用广泛。为了满足收放空间和形状要求，这种机构的结构设计和运动分析研究受到国内外学者的普遍重视，特别是对空间过约束单自由度可展机构的研究已成为目前机构学领域的研究热点之一。

Gan等［1－2］分析并制作了能紧密收拢的多杆环状可展机构模型，采用预估校正的方法求得机构在展开过程中夹角的关系，并用奇异值分解法分析了机构的奇异性。Chen等［3］研究了Bennett机构的几何特性并设计制作了能够紧密收拢的Bennett机构的另一种形式的模型。在此基础上Chen等［4－5］又进一步研究了特殊线面对称 Bricard机构的分叉点和三面对称Bricard机构的运动特性。杨毅等［6－7］设计了一种新型六面体可展机构和一种新型四棱锥单元机构。罗尧治等［8］结合四面体旋转环机构和三向对称六连杆机构的基本原理，设计了一种向外翻转开启式可展机构，并详细阐述了该可展机构的形式和设计原理。

现有研究主要集中在可展机构的几何构型方面，而对可展机构单元本身的设计及其展开运动的研究不多，目前对于可展机构的运动分析，比较常用的一种方法是采用商业软件进行仿真，对于可展桁架组合成的可展机构，一般采用几何约束建立约束方程分析其运动；对于复杂的可展机构，采用影响系数法分析其运动。本文采用D－H传递矩阵法建立可展机构的运动约束方程，并设计了四杆全铰链可展机构，该机构是一类满足收拢紧密且能展开成平面模型的单自由度过约束环状可展机构。

1 线性方程组的 Moore＿Penrose广义逆解法

设A∈Cm×n，对矩阵A进行奇异值分解可得

其中，U是m×m阶的正交矩阵，S是m×n阶的广义对角阵，V是n×n阶的正交矩阵。由式（1）求得矩阵A的Moore－Penrose广义逆为A＋＝VS＋UT，式中

其中，σ1≥σ2≥…≥σr＞0，且矩阵A的秩为r，求解线性方程组Ax＝b，当系数矩阵A是非奇异方阵时方程组的唯一解为x＝A－1b，而当系数矩阵A是奇异阵或长方阵时需采用广义逆来求解该方程组。① 当rank（A）＝rank（A∶b）时，方程组相容，方程的极小范数解与通解分别为

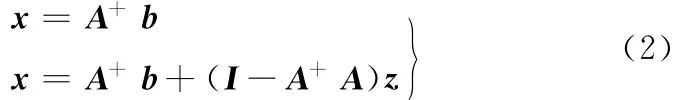
式中，z为任意n维向量；I为n阶单位矩阵。

②当rank（A）≠rank（A∶b）时，方程组不相容，方程组的最小二乘解及最小二乘通解分别为

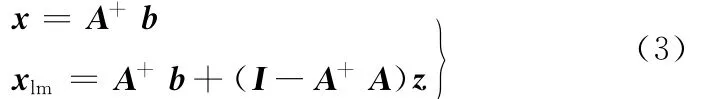
2 多杆闭环连杆机构的运动方程

由n个连杆组成的闭环机构能够运动的充分必要条件是所有连杆的变换矩阵依次相乘的结果为单位矩阵［8］，即

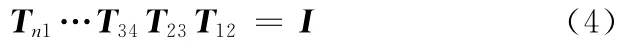
其中，变换矩阵Ti－1，i是杆i－1上的坐标系Oi－1Xi－1Yi－1Zi－1与杆i上的坐标系OiXiYiZi间的变换矩阵。如图1所示，每个铰链上固定一坐标系，对于铰链i，Zi轴沿该铰链的轴线向上，铰链i的轴线与铰链i＋1的轴线的公垂线即为Xi轴，方向由Zi指向Zi＋1，Xi轴与铰链i轴线的交点为坐标系OiXiYiZi的原点Oi，Yi轴由右手螺旋法则确定，杆长ai－1，i是由被连接的两铰链轴线Zi－1和Zi的公垂线决定的；两轴间的扭角αi－1，i是由轴线Zi－1绕公垂线Xi－1转至轴线Zi转过的角度，依据右手螺旋法则确定其方向，两连杆间的夹角θi为Xi－1轴绕Zi轴转到Xi轴的角度，其方向依据右手螺旋法则确定，Xi－1轴沿Zi轴到Xi轴的距离为相邻两杆间的偏置。

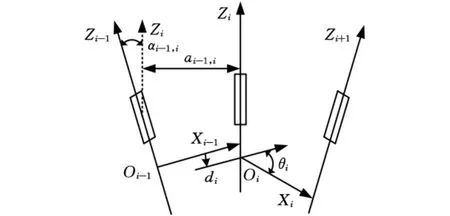
图1 由铰链连接的连杆之间的参数

坐标系Oi－1Xi－1Yi－1Zi－1与 坐 标 系OiXiYiZi之间的变换矩阵为

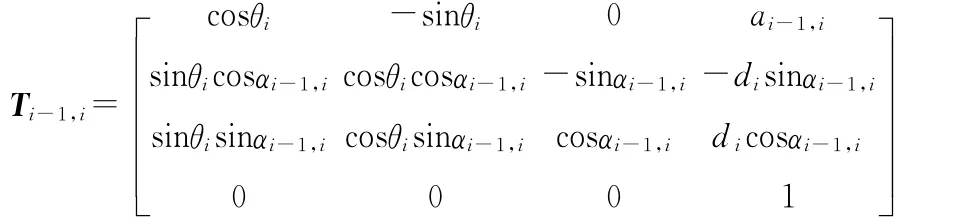
其中变换矩阵可分解成两矩阵之积，即

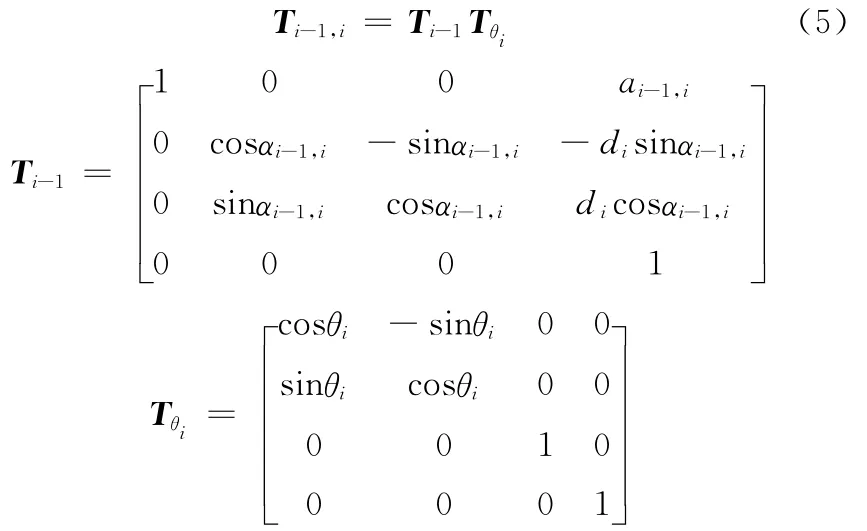
由式（5）知变换矩阵T只依赖于4个参数α、a、θ、d，所以杆系需要用这样的4个参数来描述，其中杆长和扭角两个参数描述连杆本身，他们是固定不变的；而偏置和转角两个参数描述相邻两杆的连接关系。对于转动副连接的杆系，转角是变量，而偏置是固定不变的，故在杆运动过程中Ti－1是固定不变的，而Tθi是变化的。

当运动过程中夹角有微小变化时，则有

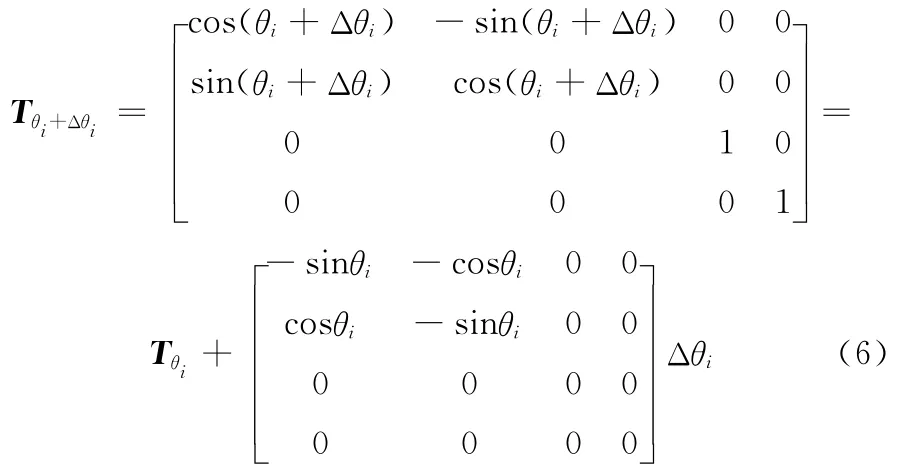
假设转角增量为Δθia，将式（6）代入式（4）并合并同类项可得

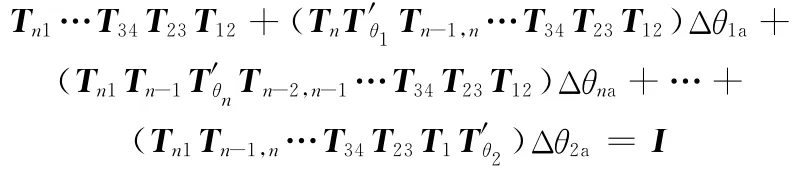
式中，I为4阶单位矩阵。

令

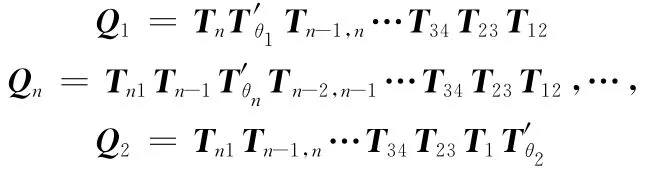
可推导得

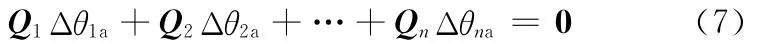
其中，0为4阶零矩阵，Qi的形式为

将式（8）代入式（7）可得如下方程组：

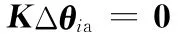
其中，Δθia＝ ［Δθ1aΔθ2a… Δθna］，雅可比矩阵K的表达式为

机构自由度大于或等于1时机构才能运动，故矩阵K为欠秩矩阵，对矩阵K进行奇异值分解，同式（1），有

显然该方程组是相容的，结合式（2）并将正交矩阵VK的最后一列代入其中，可求得线性方程组KΔθia＝0的解。估计值Δθb与Δθia成一定比例，将θib＝θi＋Δθib代入式（4）可得

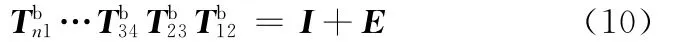
若有θn＝θi＋Δθib＋Δθic满足下式：

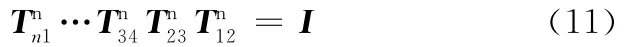
则称Δθic为校正值，展开式（10），并将式（11）代入可得

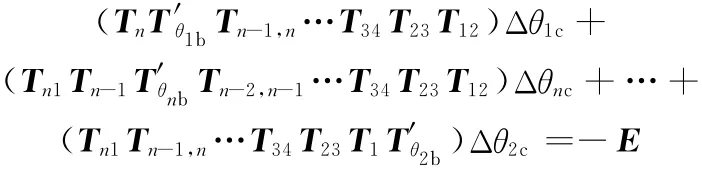
整理得

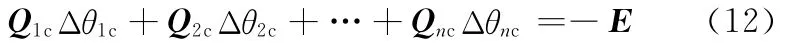
且Qic和E的形式为

将式（12）写成方程组的形式：

其中，Kb为12×n的矩阵，Δθic为n×1的向量，Eb为12×1的向量，由式（2）与式（3）可知，不管方程组（13）相容与否，其最小二乘通解或相容时的通解为Δθic＝b＋（I－b）z，这里I为n阶单位矩阵，z为任意的n维向量，z取为零向量，求得的Δθic即为校正值，从而可得θi＋1＝θi＋Δθib＋Δθic＝θi＋Δθi，将已知的夹角作为初始角度，这样不断迭代循环，直到夹角达到需求的角度从而可求出各杆之间夹角的关系。

3 算例

以四杆环状可展机构为例进行运动分析。图2、图3分别为四杆环状可展机构的展开图与收拢图，将坐标系原点O取在点A，Y轴固定在边AB上，X轴与Y轴垂直并固定在杆面ABEF上，由右手螺旋法则确定Z轴的方向。该机构是由截面为三角形的完全相同的杆经铰链内外交互链接而组成的，则同一个轴线上两条公垂线的垂点重合。图2中机构展开时轴线Z1与Z2的公垂线为U1U2，轴线Z2与Z3的公垂线为U2U3，由于4个构件完全相同，可知夹角θ3与θ1的收拢角与展开角相同，夹角θ4与θ2的收拢角与展开角相同，且图中各点在坐标系OXYZ中的坐标可由机构的几何条件确定，则各个可展角θid与收拢角θif可由机构的几何尺寸计算出。

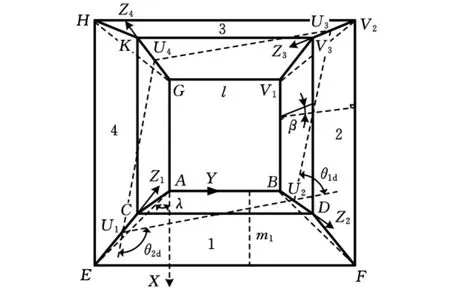
图2 机构展开图

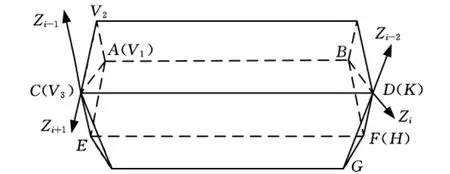
图3 机构收拢图

图2所示构件的截面夹角β变化时，机构的收拢角与展开角变化情况如图4所示，机构由收拢状态到完全展开过程中，夹角θ1由θ1f变为θ1d，夹角θ2由θ2f变为θ2d。

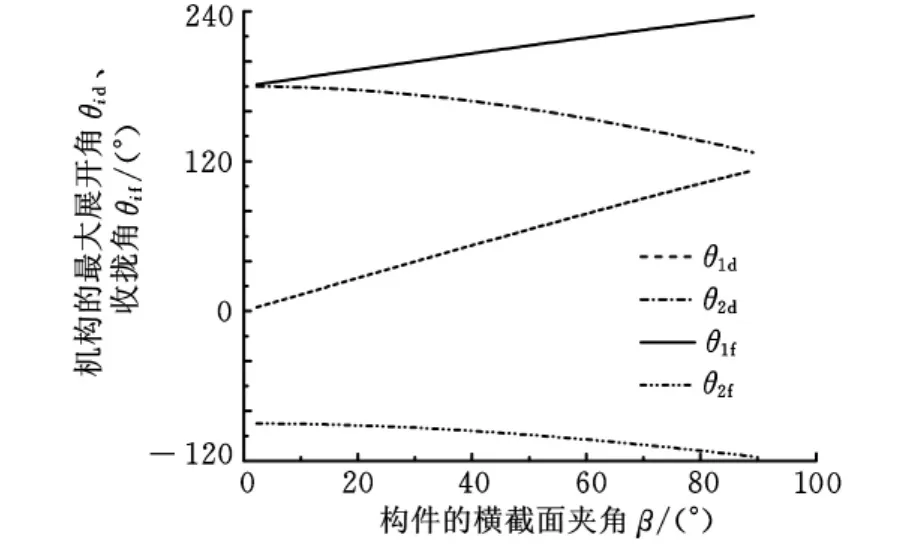
图4 夹角对机构收拢角与展开角的影响

取β＝60°时，由图4知夹角θ1在展开运动过程中是不断减小的，夹角θ2在展开运动过程中是不断增大的，故在循环过程中Δθ1＜0，Δθ2＞0总是成立的。用MATLAB编程计算可得运动过程中各个夹角的关系，如图5所示。

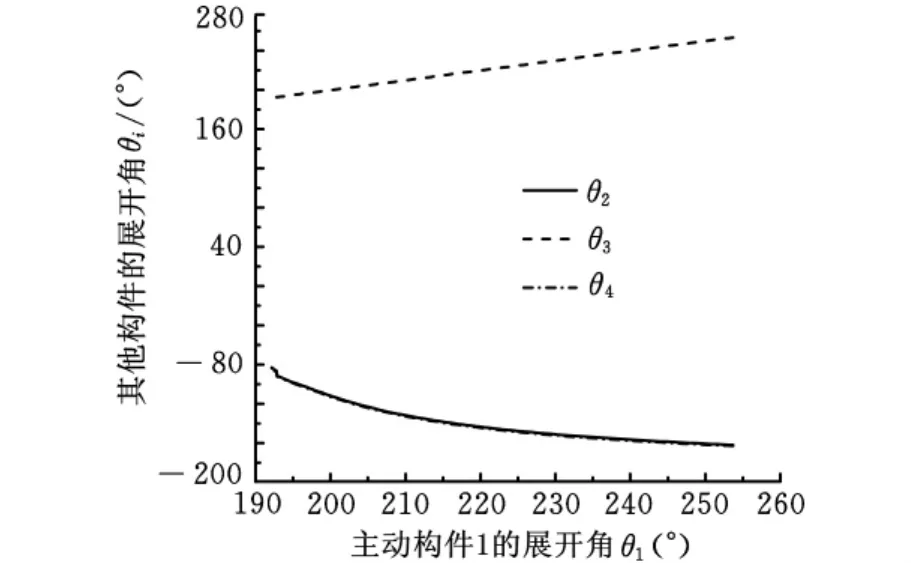
图5 机构展开过程中各个夹角的关系

4 结论

（1）分析了截面夹角β对四杆环状可展机构夹角θ在收拢状态与完全展开状态时的影响，如图4所示，随着β的增大，θ1d、θ1f增大，而θ2d、θ2f减小。

（2）由图4可知，当截面三角形底角β取允许范围内的任意值时，四杆环状可展机构由收拢状态到完全展开相同时间内夹角θ1与夹角θ2的变化范围不同，由此可知机构在展开过程中，其原型机构相邻两杆的加速度不同。

（3）将广义逆理论与空间连杆机构分析的标准方法相结合并采用预估校正循环迭代求得四杆环状可展机构在展开过程中各夹角的变化关系，如图5所示，从图中可知，在运动过程中始终有θ1＝θ3，θ2＝θ4，由此可知四杆环状可展机构在运动过程中始终有两个对称平面。

［1］Gan W W，Pellegrino S.A Numerical Approach to the Kinematic Analysis of Deployable Structures Forming a Closed Loop［D］.Cambridge：University of Cambridge，2006.

［2］Gan W W，Pellegrino S.Kinematic Bifurcations of Closed－loop Deployable Frames［C］//Proceedings of the 5th International Conference on Computation of Shell and SpatialStructures.Salzburg，2005：1－4.

［3］Chen Y，You Z.Square Deployable Frames for Space Applications［J］.Aerospace Engineering，2006，3（3）：347－354.

［4］Chen Y ，You Z，Tibor T.Threefold－symmetric Bricard Linkages for Deployable Structures［J］.International Journal of Solids and Structures，2005，42：2287－2301.

［5］Chen Y，Chai W H.Bifurcation of a Special Line and Plane Symmetric Bricard Linkage［J］.Mechanism and Machine Theory，2011，46：515－533.

［6］杨毅，丁希仑.基于空间多面体向心机构的伸展臂设计研究［J］.机械工程学报，2011，47（5）：26－34.

Yang Yi，Ding Xilun.Design and Analysis of Mast Based on Spatial Polyhedral Linkages Mechanism along Radial Axes［J］.Journal of Mechanical Engineering，2011，47（5）：26－34.

［7］杨毅，丁希仑.四棱锥单元平板式可展开收拢机构的运动特性分析［J］.航空学报，2010，31（6）：1257－1265.

Yang Yi，Ding Xilun .Kinematic Analysis of a Plane Deployable Mechanism Assembled by Four Pyramid Cells［J］.Acta Aeronautica et Astronautica Sinica，2010，31（6）：1257－1265.

［8］罗尧治，刘晶晶.基于环形连杆机构原理的可展结构设计［J］.工程设计学报，2006，13（3）：145－149.

Luo Yaozhi，Liu Jingjing .Design of Retractable Structure Based on Closed－loop Linkages［J］.Journal of Engineering Design，2006，13（3）：145－149.