缓冲材料试验台架热－水－力耦合数值模拟研究

乔 兰，曹胜飞，，陈 亮，刘月妙，谢敬礼

（1.北京科技大学土木与环境工程学院，北京 100083；2.核工业北京地质研究院，北京 100029）

高放射性废物是一种放射性强、毒性大、核素半衰期长并且发热的特殊废物，需要把它们与人类生存环境长期、可靠地永久隔离，使其在进入生物圈之前衰变到人类可接受的水平。对于高放废物的最终处置，目前公认的安全可靠，且技术上可行的方法为深地质处置，即把高放废物埋在距离地表500～1000m的地质体中，使之永久与人类的生存环境隔离，埋藏高放废物的地下工程即称为“高放废物处置库”［1－2］。高放废物处置库采用的是“多重屏障系统”设计思路，即把废物贮存在废物罐中，外面包裹缓冲材料，再向外为围岩。一般把废物体、废物罐和缓冲回填材料称为工程屏障，把周围的地质体称为天然屏障。由于地下结构开挖扰动、高放废物衰变放热、地下水渗流等作用的影响，缓冲材料在地质处置库中处于典型的热－水－力多场耦合环境。

为了揭示处置库环境热－水－力－化学多场耦合作用下缓冲回填材料行为变化的规律，国内外学者进行了大量的试验和理论研究。ZHANG Chunliang［3］利用瑞士的 Mont Terri地下实验室对Opalinus硬泥岩现场加热试验，对其受热所产生的热－水－力全程进行了模拟，深入阐述了硬泥岩在THM耦合作用下的变化特征。LI Xiangling［4］在HADES的众多现场试验中，对Boom Clay和工程屏障体系进行热－水－力性状的研究。西班牙ENRESA负责在Grimsel地下试验室实施的FEBEX试验［5－8］，研究了高放废物处置库近场所发生的THM过程，获得了大量的试验数据。刘月妙等［9］在考虑地应力、地温梯度、水力、高放废物释热和缓冲回填材料膨胀力条件下，分别模拟高放废物处置库热－力耦合、水－力耦合和热－水－力耦合条件下的温度场、应力场合应变场的变化规律，预测高放废物处置库的长期稳定性。叶为民等［10］研究了我国高庙子膨润土作为缓冲回填材料在多场耦合条件下的行为特征，建立了适合描述缓冲回填材料在热－吸力等多场耦合条件下的本构关系。

基于热－水－力多场耦合理论，针对缓冲材料试验台架，本文采用LAGAMINE数值软件对高压实高庙子膨润土在多场耦合条件下的长期性能进行了数值模拟分析，研究了温度、饱和度、吸力和膨胀力随时间的变化规律，为高放废物地质处置库的建设提供参数和借鉴。

1 热－水－力多场耦合数学模型

为了开展膨润土在多场耦合条件下的长期性能研究，本研究建立了系统的孔隙介质多场耦合数值模型。该数学模型考虑了THM条件下的耦合现象，包括热的传播（热传导和热对流）、水流场、蒸气扩散和冷凝、膨润土在非饱和条件下的力学特性等。

1.1 水、热扩散模型

膨润土由固体颗粒、液态水和气体三相组成，在高放废物深地质处置条件下，膨润土的整体平衡是一个复杂的多场耦合现象。在本数学模型中，假设不同物质质量守恒，因此在总体平衡方程中不存在物质之间的相互转化，描述系统流动体系的变量包括液态水压、气压和温度。

1.1.1 水的扩散

在缓冲材料中，水分为液态水和水蒸气，其中达西定律被用于描述液态水的流动。

式中：pw是液态水压，g是重力加速度，μw是液态水的动力粘滞系数，kint是固有渗透系数，kr，w是相对渗透系数。

水蒸气的流动传播服从菲克定律，见式（2）。

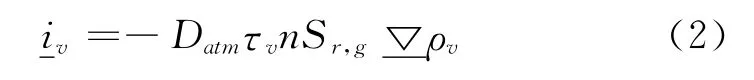
式中：Datm是摩尔扩散系数，τv是孔隙介质的折曲率，Sr，g是气体的饱和度。

1.1.2 热的传播

在本研究模型中，采用唯一的温度变量，假设非饱和土中所有的物质均处于等温状态。热的传播主要与三种物理现象有关：热传导、热对流、蒸气化现象，如式（3）所示。

式中：Γ是介质的热传导系数；cp，α是α介质的比热；L是潜热。在本研究中，为了简化，不考虑温度对热传导系数的影响。

1.2 力学模型

在缓冲材料中，饱和度和吸力变化明显，大量的研究表明，吸力对土体的力学特性有显著地影响。本文采用巴塞罗那基本模型（BBM 模型）［11］，该模型可以较好的反映吸力对力学特性的影响。

1.2.1 屈服面

BBM模型是在剑桥模型的基础上发展起来的，为了考虑饱和度对土体力学特性的影响，吸力被作为一个独立的变量引入到模型中。因此，模型的塑性屈服面可以在（p，q，s）三维空间中进行描述，其主要包括以下内容。

在（p，q）平面内，对于给定的吸力值，塑性屈服面可以写成如下的形式：

式中：p是平均净应力，q是偏应力，M是临界状态线斜率，ps是土体的张拉强度，p0是土体在吸力为s时的预固结压力。

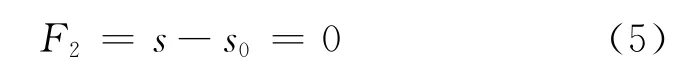
式中：s是吸力，s0是SI屈服面的硬化参数，代表历史上土体承受的最大吸力值。

1.2.2 硬化准则

该模型中，塑性屈服面的硬化演变取决于总体的塑性体积应变增量，由硬化参数和s0控制，如式（6）、式（7）所示。

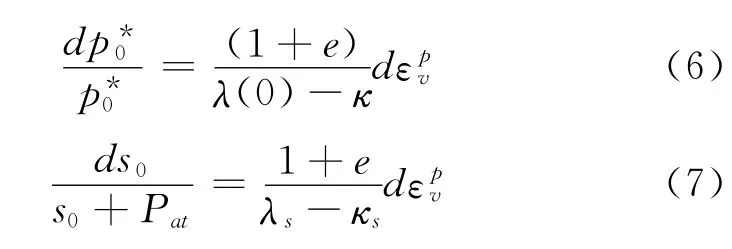
式中：e是土体的孔隙比，Pat是大气压，λs和κs分别是弹性和塑性刚度参数。

2 缓冲材料热－水－力耦合试验台架模拟和数值分析

2.1 缓冲材料试验台架系统

试验台架系统由进水系统、试验腔体、加热系统和数据采集系统组成。试验材料为内蒙古高庙子膨润土，传感器包括温度、温湿度、土压力、孔隙水压力传感器。简化如图1所示。试验中，加热器由室温逐渐加热至90℃并恒定运行，进水压力维持在0.05MPa。

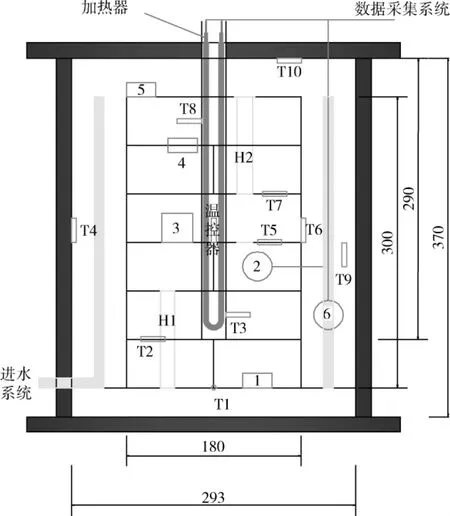
图1 试验结构剖面图

2.2 边界条件

考虑到试验台架是标准的轴对称结构，作为近似简化，取纵向截面的一半进行数值模拟，计算域尺寸如图2所示，该模型有1447个单元，4161个节点。

系统初始温度为20℃室温，膨润土初始饱和度为48%，孔隙比为0.57。根据高庙子膨润土的土水特征曲线，初始吸力确定为80MPa。为了得到更好的数值收敛性，气压在计算中被设定为常数。

关于边界条件，计算域的周边位移固定，试验台架与周围环境的热对流现象，由边界热交换单元来模拟。模拟过程分两部分进行。

2.1 两组血浆NT-proBNP水平比较 病例组患儿的NT-proBNP水平在治疗3 d、治疗7d 、治疗14 d时均显著低于组内治疗前(F=176.405，P<0.05)，病例组患儿的NT-proBNP水平在治疗前、治疗3 d、治疗7 d、治疗14 d时均显著高于对照组(F=286.557，P<0.05)。见表1。

1）第一步，在10小时内，计算域与加热器接触边界温度从室温（20℃）上升至预定加热温度90℃，同时外侧水压从初始吸力值上升到0.05MPa。

2）随后3年内，边界条件保持稳定，模拟膨润土内部的物理力学变化过程。

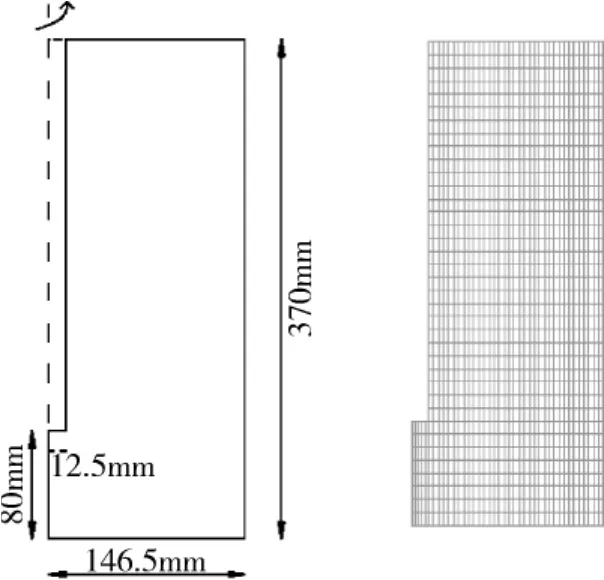
图2 几何和网格划分图

2.3 参数确定

水、热特征参数基于CHEN Bao的试验成果［12］，通过对试验数据拟合，高庙子膨润土吸力与饱和度的关系可以由式（8）进行描述。

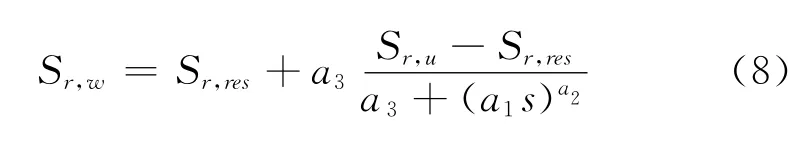
式中：Sr，u是土体的最大饱和度，Sr，res代表在吸力控制下土体可以达到的最小饱和度。根据试验结果，Sr，u和Sr，res数值确定为1.0和0.1，通过对试验结果的拟合，式中参数a1＝3.5×10－6Pa－1，a2＝0.8，a3＝90。

根据YE Weimin的试验结果［13］，高庙子膨润土的固有渗透系数kint＝2.0×10－21m2，相对渗透系数曲线如式（9）所示。

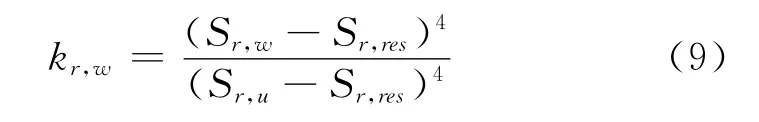
在热传导试验中，对不同饱和度的膨润土试样进行热传导系数的测量，根据试验结果，可采用如下线性关系来反映热传导系数随饱和度的变化。

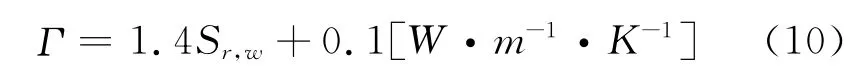
土体其他水、热参数如表1所示。

Cui开展了不同吸力和温度条件下高庙子膨润土的相关力学试验［15］。根据λ（s）随吸力的变化规律，参数γ和β得到了确定。表2汇总了高庙子膨润土的主要力学参数。

2.4 数值模拟结果及分析

依据构建的热－水－力多场耦合数学模型，采用LAGAMINE多场耦合软件，完成了缓冲材料试验台架热－水－力多场耦合数值模拟。

试验台架中部水平方向温度随时间的变化趋势如图3所示。由图中可以发现，在试验过程中温度不断升高，并且距离加热器越远，加热器的干燥作用越小，升温幅度趋于平缓。另外，数值结果表明热边界单元可以很好的模拟在热对流作用下试验设备外部温度不断升高的现象。

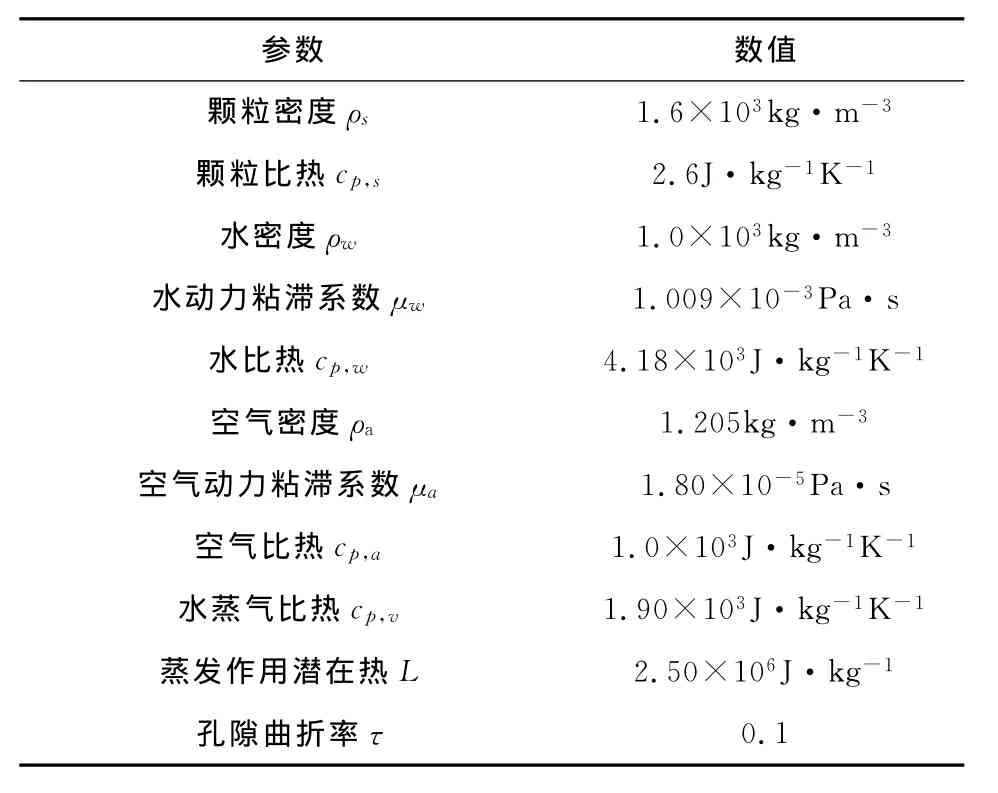
表1 高庙子膨润土基本物理参数［14］

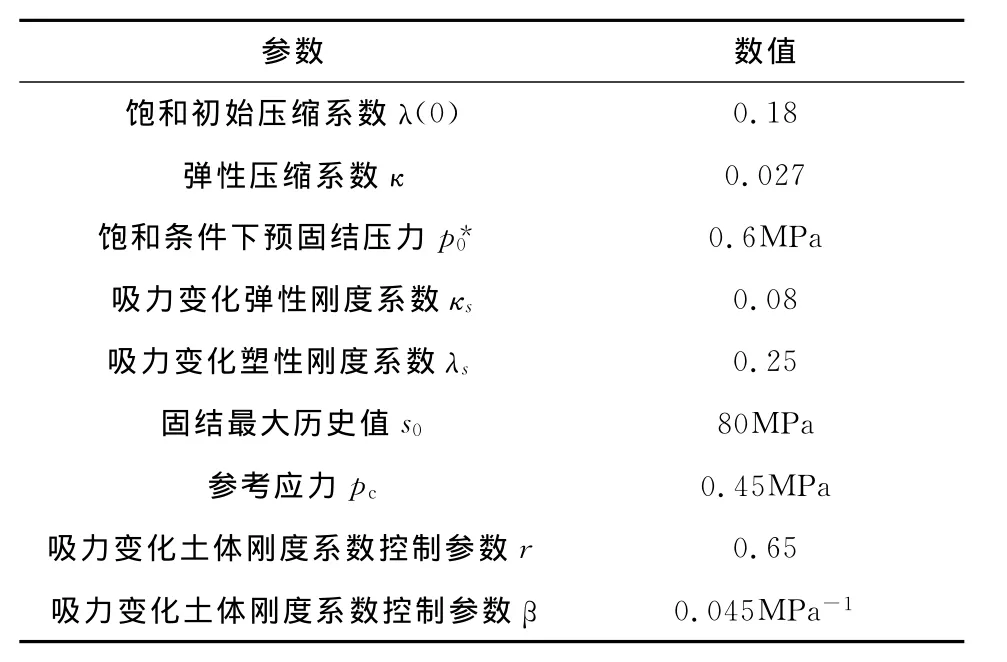
表2 高庙子膨润土力学参数［14］

图3 水平向温度分布随时间变化趋势图

在水平方向上，吸力分布随时间的变化趋势如图4所示。由图4可以看出，随着膨润土的饱和，吸力值逐渐降低，且距离加热器越近，降低的趋势越明显，特别是在加热器附近区域，在试验前期阶段，吸力值大于初始吸力值，意味着在这一区域存在着先干燥再饱和的过程。

这一现象可以通过图5更直观的反映出来。如图5所示，在加热器附近的A点，吸力值首先增加，然后逐渐减小。此干燥－饱和过程可以通过水蒸气蒸发引起的干燥作用和水的渗透导致的饱和作用的相互关系来解释。在试验初期，随着温度的升高，靠近加热器的水分蒸发，并通过水蒸气扩散向外侧传播。而由于极低的渗透系数，水的渗透作用相对较弱，因此整体上表现出干燥现象。随着试验的进行，裂隙水通过渗透作用逐步抵达这一区域并起主导作用，因此随后表现出饱和现象。

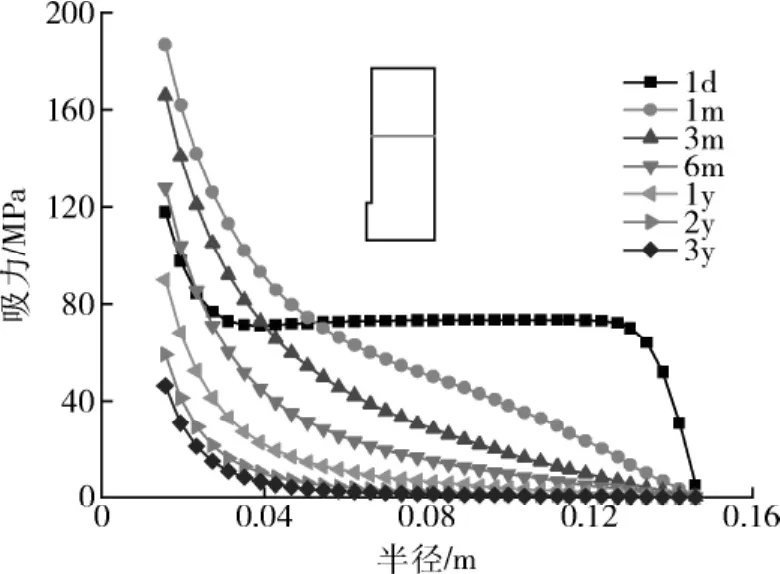
图4 水平向吸力分布随时间变化趋势图

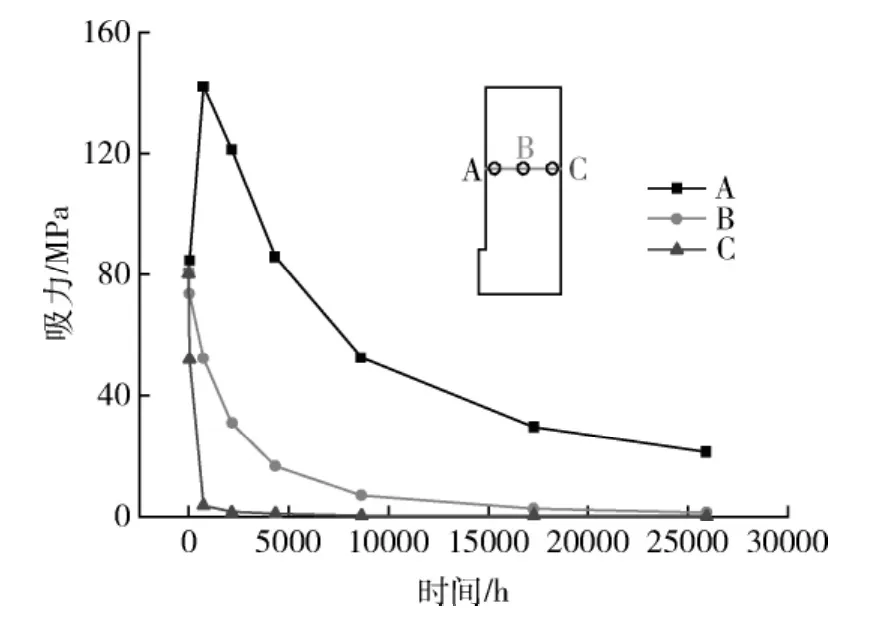
图5 特征点吸力分布随时间变化趋势图

水平方向上A、B、C三点处的膨胀力随时间的变化趋势如图6所示。由图6可以看出，在试验初期膨胀力增加很快，随后趋势逐渐减弱。且靠近进水管C点处，由于饱和度较大，产生的膨胀力最大，三年后，膨胀力大概为2.5MPa左右。考虑到饱和过程尚未结束，膨胀力上升曲线并未变得平缓，故该数值尚未达到膨胀力的最大值。

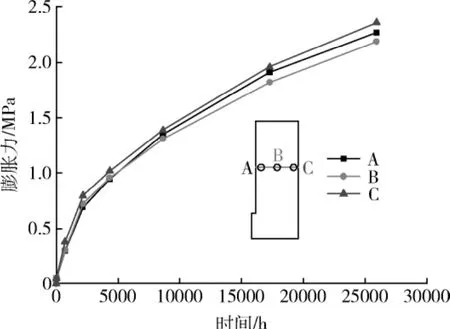
图6 特征点膨胀力随时间变化趋势图

3 结论

通过对缓冲材料中型试验台架模拟结果的定性分析，可以认为本数值计算方法可以很好地描述高庙子膨润土的热－水－力多场耦合特性。模拟结果得出以下结论。

1）温度场随时间变化逐渐升高，且随着距离加热器越远，升温趋势逐渐变缓。

2）随着膨润土的饱和，土中吸力不断降低，但是在试验前期阶段，由于加热水蒸气蒸发引起的干燥作用和水的渗透导致的饱和作用的相互影响，靠近加热器的区域存在一个先干燥后饱和的过程。

3）在水的渗透作用下，高庙子膨润土随时间逐渐饱和。不过由于其极低的渗透系数，三年后膨润土块依然没有完全饱和。三年后，膨胀力大约达到2.5MPa，膨胀力上升曲线并未变得平缓，故该数值尚未达到膨胀力的最大值。

这里需要说明的是，由于缺乏足够的试验数据，本研究仅进行了定性分析。因此，本数值模拟分析只可以被作为对提出的数值计算模型的初步验证。随着试验的进行，将会展开进一步的数值研究。

［1］王驹，陈伟明，苏锐，等.高放废物地质处置及其若干科学问题［J］.岩石力学与工程学报，2006，25（4）：801-812.

［2］潘自强，钱七虎.高放废物地质处置战略研究［M］.北京：原子能出版社，2009.

［3］ZHANG Chunliang，Rothfuchs Tilmann，Wieczorek Klaus，et al.Monitoring and modeling of responese of the Opalinus clay to heating［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（4）：659-669.

［4］Li Xiangling，Bernier Frederic，Bel Johan.The Belgian HLW repository design and associated R＆D on the THM behavior of the host rock and EBS［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（4）：681-692.

［5］A.Lloret，M.V.Villar.Advances on the knowledge of the thermo-hydro-mechanical behaviour of heavily compacted“FEBEX”bentonite［J］.Physics and Chemistry of the Earth，2007，32，701-715.

［6］J.Samper，Liange Zheng，Luis Montenegro，et al.Coupled thermo-hydro-mechanical models of compacted bentonite after FEBEX in situ test［J］.Applied Geochemistry，2008，23，1186-1201.

［7］E.E.Alonso，J.Alcoverro，F.Coste，et al.The FEBEX benchmark test：case definition and comparison of modeling approaches［J］.International Journal of Rock Mechanics ＆Mining Sciences，2005，42，611-638.

［8］M.Victoria Villar，Antonio Lloret.Dismantling of the first section of the FEBEX in situ test：THM laboratory tests on the bentonite blocks retrieved［J］.Physics and Chemistry of the Earth，2007，32，716-729.

［9］刘月妙，王驹，蔡美峰，等.高放废物处置库近场热－水－力耦合长期稳定性分析［C］.第二届废物地下处置学术研讨会论文集，2008.

［10］叶为民，万敏，陈宝，等.非饱和膨润土水－力学性状的温度效应研究进展［C］.第二届废物地下处置学术研讨会论文集，2008.

［11］Alonso.E.E，Gens.A，Josa.A.A constitutive model for partially saturated soils［J］.Geotechnique，1990，40（3）：405-430.

［12］CHEN Bao，QIAN Lixin，YE Weimin，et al.Soil-water characteristic curve of Gaomiaozi bentonite［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（4）：788-793.

［13］Ye W M，Cui Y J，Qian L X，Chen Bao.An experimental study of the water transfer through confined compacted GMZ bentonite［J］.Engineering Geology，2009b，108（3/4）：169-176.

［14］Liang Chen，Ju Wang，Yuemiao Liu，et al.Numerical thermohydro-mechanical modeling of compacted bentonite in Chinamock-up test for deep geological disposal［J］.Journal of Rock Mechanics and Geotechnical Engineering，2012，4（2）：183-192.

［15］Cui yujun，Tang Anhminh，Qian Lixin，et al.Thermalmechanical behavior of compacted GMZ bentonite［J］.Soil and Foundations，2011，51（6）：1065-1974.