采选冶联合企业技术指标整体动态优化的方法
2013-07-25刘保顺王向前
刘保顺,王向前
(1.北京科技大学金属矿山高效开采与安全重点实验室,北京 100083;2.北京科技大学土木与环境工程学院,北京 100083)
根据钢铁协会对重点大中型钢铁企业统计[1],2012年一季度,全行业净利润亏损10.34亿元,由钢铁生产主业亏损变为行业亏损,亏损面达到33%;而亏损企业亏损额达到90.98亿元,同比增加31.4倍。钢铁企业亏损的原因主要有:一方面钢材需求减弱,钢材价格下降;另一方面,由于铁矿石、煤炭、电力等价格的上升,导致钢铁生产成本增大。在此形势下,钢铁企业更要精打细算,做好“过冬”的准备。
对采选冶联合企业而言,由于公司缺少系统的核算,企业的生产技术指标,如边界品位、工业品位、精矿品位、入炉品位等,一般是根据经验而定的。炼铁厂希望精矿品位越高越好,但矿山担心亏损,不愿提高精矿品位;而精矿品位又受制于前序工艺地质、采矿的约束。显然,只有兼顾矿山和炼铁效益,才能使企业获得最佳效益。
1 系统整体优化的流程
采选冶联合企业中,许多技术指标间相互关联。调整某一指标时,与之相关联的其它指标发生相应的改变,优化中要建立反映这种动态关系的数学模型。企业制订生产技术指标时,必须从企业全局出发,统筹兼顾。例如降低圈定矿体的品位指标,有利的是矿体储量增加,采出矿石量增加;不利的是矿体平均品位下降,采出品位下降,选比上升。同样,提高精矿品位,有利的是能提高烧结矿(或球团矿)品位,从而提高入炉品位,降低焦比,进而降低生铁成本;但不利的是资源回收率降低,选矿成本增加。显然,只有兼顾矿山和炼铁效益,才能使企业获得最佳效益[2]。图1是系统整体优化的整体流程图。

图1 系统整体优化框图
2 动态数学模型的建立
2.1 储量模型的建立
当调整边界品位和工业品位指标时,需要重新圈定矿体,以估算新品位指标下矿体的储量和地质平均品位。当边界品位和工业品位指标的组合方案较多时,即使是借助于Surpac、3DMine等矿业软件,重新建立实体模型和块体模型,其工作量也会大到难以承受的地步。为此,可通过数理统计的方法加以实现[3-4]。具体方法如下。
2.1.1 以积分法求储量系数
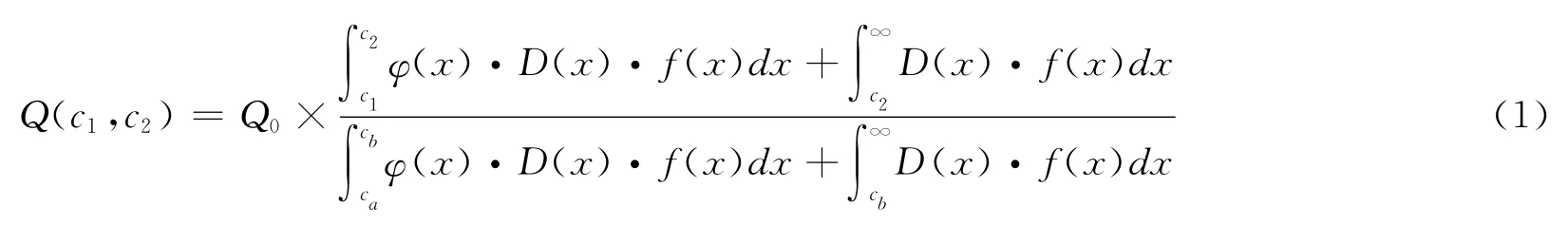
式中:Q(c1,c2)为边界品位c1,工业品位c2时,矿体储量(Q0=1时,该式可称为储量系数);φ(x)为介于边界品位和工业品位的非经济储量的样品,进入经济储量的概率,见式(2);D(x)为以样品品位x为自变量求矿石体重的函数;f(x)为样品概率密度函数,由样品品位分布统计求得;c1,c2为新品位指标下的边界品位和工业品位;ca,cb为原来品位指标下的边界品位和工业品位;Q0为边界品位和工业品位分别是ca,cb时,用其他储量计算方法求得的矿体的储量。
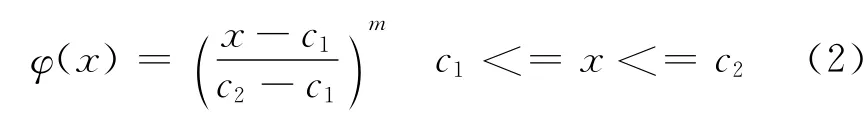
式中:m为随矿床地质条件而定,对具体矿山可通过参数估值求得。
2.1.2 以积分法求矿体地质平均品位

式中:C(c1,c2)为边界品位为c1,工业品位为c2时的矿石平均品位;其他符号同前。
2.1.3 通过回归分析建立求储量和平均品位的数学模型
使用式(1)、式(3),求得多组不同品位指标下的储量和平均品位,然后以边界品位和工业品位为自变量,分别以储量和平均品位为因变量,建立回归方程。这样当取不同的边界品位和工业品位时,可求得相应指标下的矿体储量和地质平均品位。
2.2 建立损失率和贫化率的数学模型
圈定矿体的品位指标发生变化后,矿体形态发生变化。对于某些采矿工艺,损失率与贫化率存在相关关系。调整贫化率时,损失率会发生相应的改变,此情况下,建立以贫化率求损失率的数学模型。根据储量模型和损失率与贫化率模型,可以计算得到不同品位指标下,采出矿石量和采出品位。
2.3 建立选矿数学模型
使用选厂正常生产下近几个月的日报,建立入选品位与选比、精矿品位的数学模型,入选品位和选比一般呈反相关关系。
通过选矿模型分别计算出不同入选品位、入选矿石量下的精矿量和精矿品位。
2.4 烧结矿、球团矿技术经济模型
边界品位和工业品位改变后,引起自产精矿的产量、成分和成本的变化。在不改变其其它配料的情况下,烧结的成本、成分和产量也要发生变化[5]。
2.4.1 烧结矿的产量
基于烧结过程中的物料平衡,列出方程式(4),用于计算烧结矿的产量。

式中:Q为烧结矿产量;∑K为铁矿粉和各种含铁原料的干重;∑F为石灰石、白云石等熔剂的用量;C为焦粉、无烟煤粉等燃料;S为以上三种原料中的烧损;Y为烧结过程中氧的变化。
2.4.2 石灰石用量
在设定烧结矿碱度情况下,式(4)∑F可通过碱度平衡求得。如求石灰石用量,根据设定的烧结矿碱度,由式(5)计算。

式中:F为石灰石消耗量;R为烧结矿碱度;∑SiO2为各种原料、燃料带来的SiO2;∑CaO为各种原料、燃料带来的CaO;(CaO)F为石灰石中有效CaO。
2.4.3 烧结过程中氧的变化量
根据烧结用铁矿粉种类和工艺的不同,氧的变化量Y可能是负值,也可能是正值。负值表示烧结过程中三价铁升高,为氧化反应;正值时为还原反应。由式(6)计算。

式中:Y为烧结过程中氧的变化;∑FeO为铁矿粉和熔剂、燃料带来的FeO;Q为烧结矿产量;(FeO)为设定的烧结矿中FeO的含量。
2.4.4 烧结矿的经济模型
基于其生产成本构成,用式(7)建立烧结矿的经济模型。
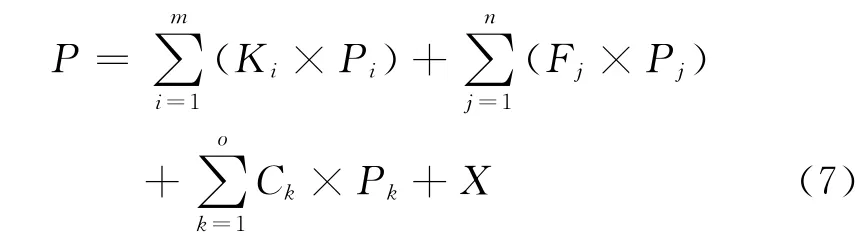
式中:P为烧结矿的成本;Ki为第i种含铁料的单耗;Pi为第i种含铁料的单价;Fi为第j种熔剂的单耗;Pj为第j种熔剂的单价;Ck为第k种燃料的单耗;Pk为第k种燃料的单价;X为单位烧结矿的加工费。
烧结矿的含铁品位首先决定于配料中铁矿粉的品位。在碱度(CaO/SiO2)不变的条件下,铁矿粉品位愈高,烧结矿的品位也愈高。
2.4.5 球团矿的经济模型
球团矿的配料,除使用膨润土而不用燃料外,其余与烧结矿基本上都相同,故其技术经济模型的建立过程与烧结矿基本相同。
2.5 炼铁数学模型
炼铁界有一个传统的说法:入炉矿含铁品位升高1%,焦比降低2%,高炉利用系数提高3%。它反映了炼铁的基本规律,但不够精确。通过建立高炉的技术经济模型,可更加准确地反映出入炉品位、生铁产量、生铁成分、生铁成本、燃料比、冶炼强度、熟料率、喷吹率、渣铁比等的动态关系[5]。
2.5.1 炼铁技术模型
根据铁平衡原理,在已知含铁原料供应量条件下,通过式(8),求出生铁的产量。

式中:∑If为铁矿、燃料带来的Fe;Tf为生铁中含Fe;Zf为炉渣中含Fe;Df为炉尘中含Fe;Lf为铁的机械损失。
根据能量平衡,列出方程式(9)。

式中:Qr为碳素在风口前燃烧放热;Qf为高温热风带来的热能;qh为还原反应吸热;qt为高温铁水带出热能;qy为高温液态炉渣带出热能;qm为炉顶煤气带出热能;qs为冷却水带走和炉壳散热。
将式(8)、式(9)两个方程式联合求解,可计算出生铁产量和焦比。
2.5.2 炼铁经济模型

式中:CHM为生铁成本;∑K为含铁原料的单耗;j1为含铁原料的单价;∑R为燃料的单耗;j2为燃料的单价;J为每吨生铁的加工费。
2.6 地采选冶综合技术经济模型
所谓综合技术经济模型,就是通过计算机编程,构建上述技术经济模型及其它的地质、采矿、选矿、烧结、球团、炼铁等环节的技术经济指标间动态的关联关系。当边界品位、工业品位等取不同方案时,通过该模型,可求得不同方案下的目标值及其它技术经济指标。
3 多目标综合评价
在决策生产技术指标时,既要考虑经济效益,如生铁成本,也要考虑资源效益,如精矿金属量。企业可根据实际的情况,设置寻优范围和约束条件。如设置边界品位和工业品位都从18%到25%,步长1%;设置的约束条件有:选矿生产能力、高炉炉渣碱度、烧结矿(球团矿)产量、生铁产量等。
在进行多方案决策时,会出现生铁成本低(高)的方案,精矿金属量高(低)的情况,既决策目标的峰值出现在不同的方案中,可通过模糊综合评判法解决此问题[3]。
4 结论
多年来,通过在首钢、酒钢等企业开展生产技术指标优化的研究,证明以上方法是切实可行的。采选冶联合企业在优化各生产技术指标时,应遵循以下原则:不能从某一部门的局部利益上做出决策,而是要从企业全局算经济账;通过分析各技术指标间的相关关系,建立它们间的数学模型;优化中既要考虑经济效益,也要考虑资源效益,从多目标考虑对问题进行决策。
[1]中国钢铁工业协会.一季度钢铁业再现全行业亏损,预计上半年会好转[N].证券时报,2012-4-18.
[2]石云良,麦笑宇,曹佳宏,等.铁精矿品位的多目标优化[J].矿冶工程,2003,23(2):46-48.
[3]刘保顺,李克庆,袁怀雨.矿产经济学[M].北京:冶金工业出版社,2009.
[4]李克庆,牛京考,袁怀雨,等.白云鄂博铁矿磁铁矿石品位指标的优化[J].北京科技大学学报,2007,29(3):333-337.
[5]贺友多.炼铁学[M].北京:冶金工业出版社,1994.
