改进的灰色预测模型在煤矿成本预测中的应用
2013-07-25侯运炳汪健民石森森李照栋
侯运炳,汪健民,2,张 晓,石森森,李照栋
(1.中国矿业大学 (北京)资源与安全工程学院,北京 100083;2.潞安集团王庄煤矿,山西 长治 046031)
先进、合理的成本控制目标是有效指导企业成本控制的导向和衡量其效果优劣的准绳。在煤矿成本管理的过程中,不仅要对煤矿企业的成本进行分析,更需要在此基础上对煤矿企业的成本变动情况做出科学、合理的预测。因此,科学预测、进而指导煤矿企业正确决策是有效实施成本控制、提升企业市场竞争力的重要环节[1]。
由我国学者邓聚龙提出的基于灰色理论的GM(1,1)模型是煤矿企业成本预测中较为有效地方法,但是传统的GM(1,1)模型的预测结果是一条光滑的指数曲线,难以反映出序列的随即变动性[2]。GM(1,l)模型在处理单调非负数据序列时效果很好,预测精度较高,对负数序列需要进行处理(即通过平移变换使序列的元素为正),对于振荡数据序列,其预测效果则不好,这是因为经过GM(l,l)模型算出的序列具有单调性,还原回去的序列也具有单调性[3]。
本文在以上研究的基础上对传统的灰色系统模型通过加速平移变换和几何平均变换而进行了改进,将随机振荡序列变为适合建立GM(1,l)模型的序列模式,然后再建立GM(1,l)模型,以提高模型的模拟和预测精度,弥补了数据不足、震荡幅度大的缺点,大大提高了预测效果。
1 GM(1,1)模型
单序列一阶线性灰色模型GM(1,1)的微分方程
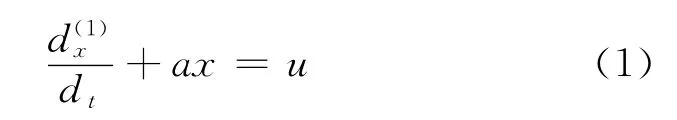
式中,a为响应系数,u为控制项,它们均为特定系数。
为了确定上述系数,首先对原始时间序列x(0)(k)采用累加法生成新的时间序列x(1)(k),并对其进行如下处理:
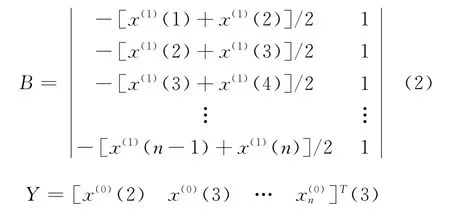
其中
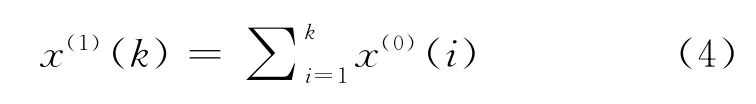
x(0)(k)为原始时间序列,k=1,2,3,…,n。则有:
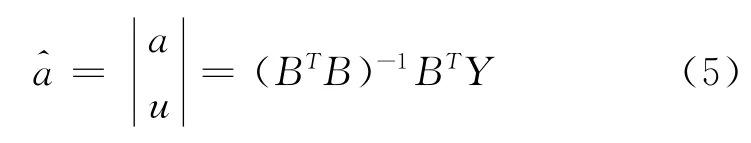
确定了系数之后,可以求的微分方程(1)的解(也称为时间相应函数(t)。
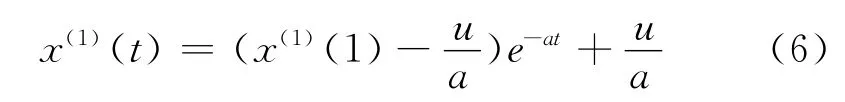
式(6)即为经过一次累加生成的预测模型,为了得到最后的结果,还需做一次累减生成,求出原始数列的预测值:
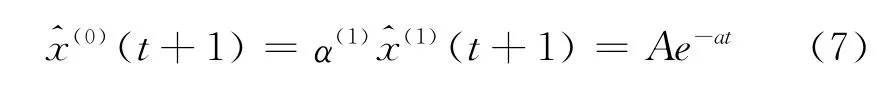
式中
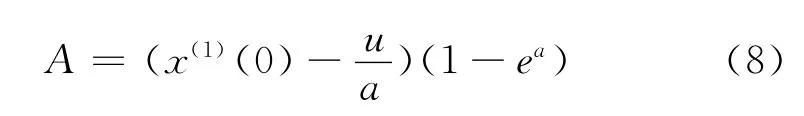
当灰色预测完成以后,我们要通过对其进行精度的检验,以确定其模拟预测的可靠性。一般进行精度检验主要有残差值检验、相对误差检验、平均相对误差检验、平均精度检验。
2 GM(1,1)模型的改进
对原始数列进行变换。
2.1 加速平移变换
设原始数据序列为x={x(1),x(2),…x(n)},记T=M-m,则称变换
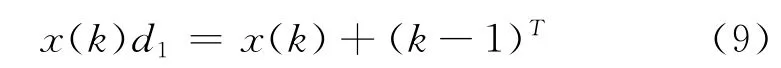
k=1,2,…,n为加速平移变换,记为D1,其中
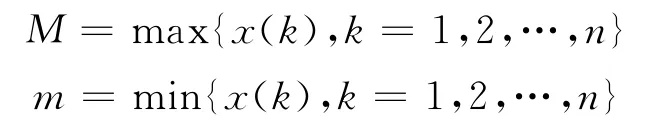
任意的数据序列x经过加速平移变换后为一次单调序列,xD1为单调递增序列。
2.2 几何平均变换
设原始数据序列为
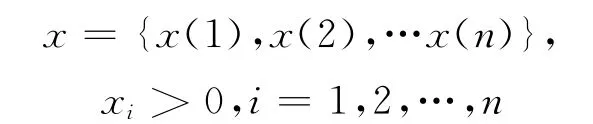
则称变换
k=0,1,2,…,n为几何平均变换,记为D2。
任意的数据序列x经过几何平均变换后,可使其随机性减弱,而经过几何平均变换后的序列保持了原有序列的单调性[3]。
2.3 分析
任意的原始数据序列x经过加速平移变换都可以变成一个单调递增序列xD1,在经过几何平均变换后不仅减弱其随机波动性,大幅度提高了数据序列的适应性,而且还可以保证数据序列xD1的单调性。因此,在原始数据序列进行处理之后所建立的GM(1,1)模型,可以很大程度上提高预测的准确度[4]。
3 构建模型
1)原始数据序列x(0)={x(0)(1),x(0)(2),…,x(0)(n)}为随机波动序列。
2)对x(0)进行加速平移变换得到序列x(1)={x(1)(1),x(1)(2),…,x(1)(n)}。
其中
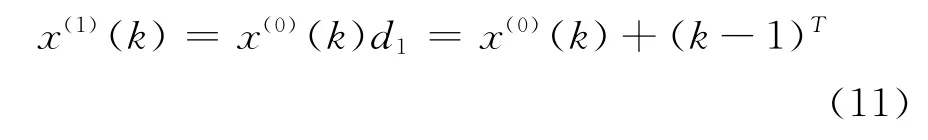
3)再对x1进行几何平均变换,得到序列Y(0)={y(0)(1),y(0)(2),…,y(0)(n)}。
其中,
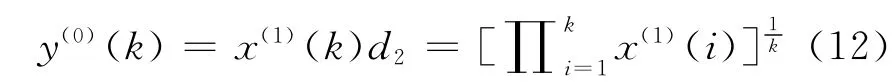
4)累加法生成新的时间序列Y(1)
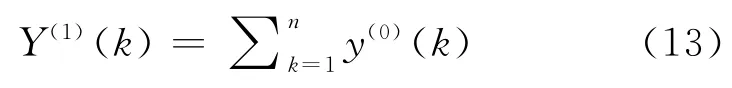
5)确定系数(matlab计算)
用最小二乘法可以的到微分方程的系数:
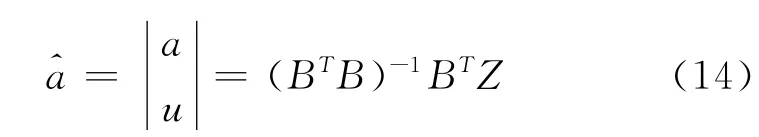
其中:
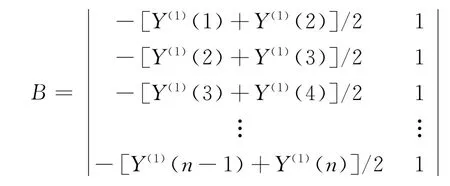
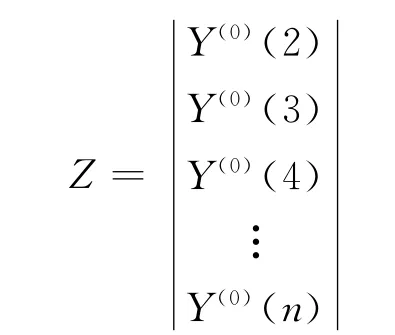
6)灰色预测模型
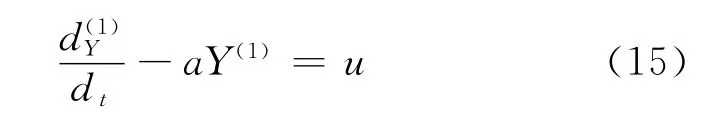
累加时间数列预测模型:
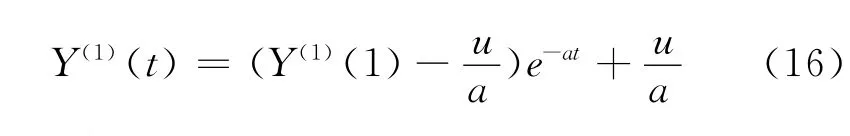
时间响应序列为:
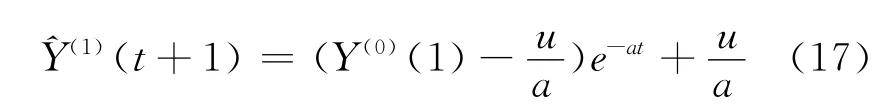
将做一次累减生成,将其还原成预测模型:
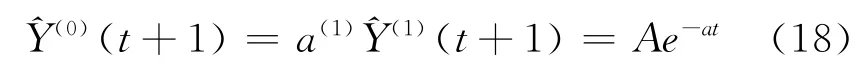
其中:
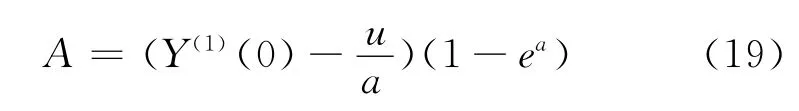
7)还原
进一步还原得到最终的预测模型:
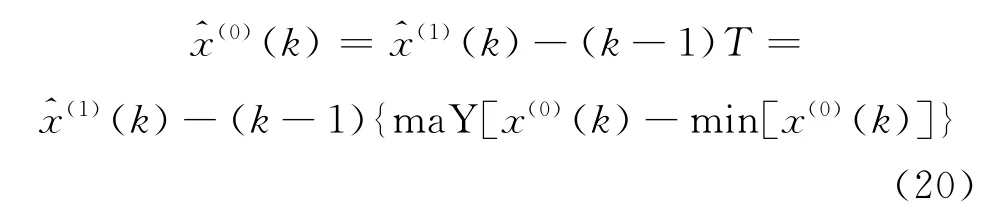
8)精度检验
对预测的结果应用残差值和相对误差来判断此模型的预测精度。
4 在煤矿成本预测中的应用
4.1 资料收集
某矿2003~2011年吨煤成本数据见表1。
考虑到通货膨胀造成的物价上涨、国家工资调整等外界因素的影响,以2003年的生产资料价格水平为基数,按照物价指数等对原数据进行调整,得到可用于预测的数据[5]。
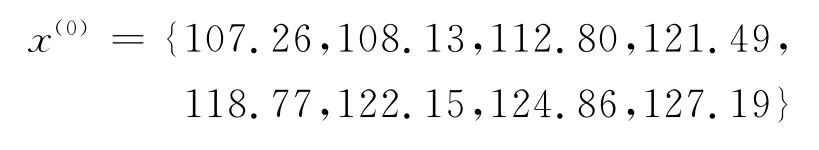

表1 煤矿2003~2011年单位成本动态变化表/(元/t)
4.2 数据处理
对原始数据序列x(0)进行加速平移变换,得到序列x(1);再对x(1)进行几何平均变换,得到序列Y(0);累加法生成新的时间序列Y(1)。
4.3 建立模型
1)确定系数(matlab计算)
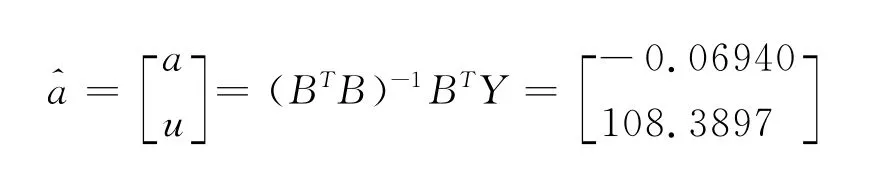
2)利用GM(1,1)模型,得出

3)还原

进一步还原得到最终的预测模型:
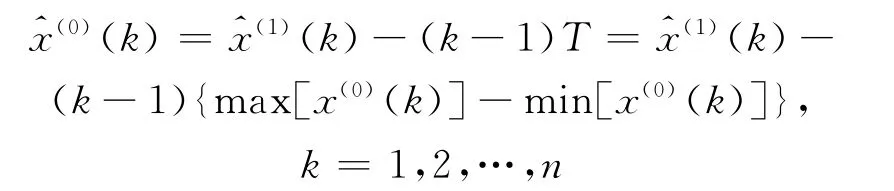

4.4 精度检验
对预测的结果应用残差值和相对误差来判断此模型的预测精度。
4.5 两预测模型的比较分析
将由原始数据序列直接建立的GM(1,1)模型与改进以后生成的新的数据序列建立的GM(1,1)模型的预测结果进行比较,比较结果见表2。由表2可以看出,改进后的模型使得平均相对误差大大下降,通过绘制出两种预测方法的拟合曲线(图1)可以看出,改进后的GM(1,1)模型预测结果更加接近原始序列的水平,大大提高了预测精度。
为了进一步验证该方法,将改进的灰色预测模型其应用于其他矿的原煤成本预测,同样得到很好的效果。但限于篇幅,在这里就不一一列举。
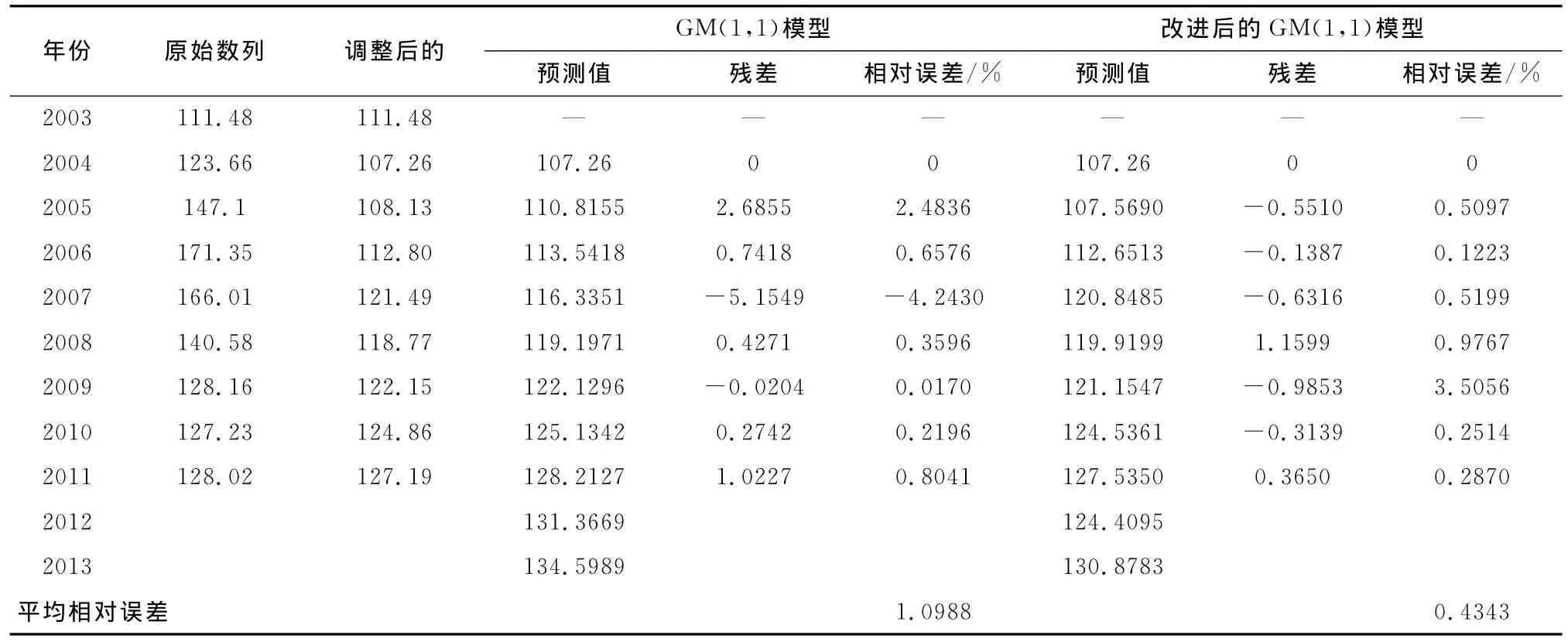
表2 模型预测值及误差分析
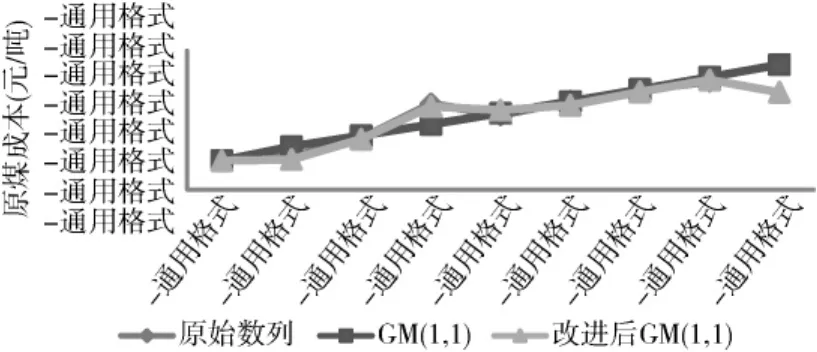
图1 预测的拟合曲线图
5 结论
1)由于煤炭行业的发展的初始阶段,没有很好的成本管理体系,造成很多数据的缺失。通过对原始数列进行变换有效地弱化了原始数列的波动性,并将其转化为递增序列,为GM(1,1)模型的建立奠定了良好的基础。
2)煤炭成本预测是基于随机振荡序列的灰色预测,适宜采用改进的GM(1,1)模型,以提高其预测精度。随着成本管理越来越被重视,该方法可以被煤炭企业应用于煤炭成本预测,进而改善煤矿的成本管理工作。
3)从预测结果可以看出,在今后的一段时期内煤炭的成本稳中有升。随着经济的发展,煤炭行业的生产运营成本也在逐步提高,煤炭企业要在激烈的市场竞争中保持优势,必须对企业进行有效的成本管理。
[1]林万祥.成本论[M].北京:中国财政经济出版社,2001.
[2]邓聚龙.灰色理论基础[M].武汉:华中科技大学出版社,2002.
[3]钱吴永,党耀国.基于振荡序列的 GM(1,1)模型[J].系统工程理论与实践,2009,29(3):149-154.
[4]赵宇哲,武春友.灰色振荡序列GM(1,1)模型及在城市用水中的应用[J].运筹与管理,2010(19):155-166.
[5]杨米会,郭道燕.灰色预测模型在煤矿成本预测中的应用[J].价值工程,2012(2):128-129.
