Stiefel流形上的梯度算法及其在特征提取中的应用

章建军*① 曹 杰② 王源源①



Stiefel流形上的梯度算法及其在特征提取中的应用

章建军曹 杰王源源

(南京航空航天大学电子信息工程学院 南京 210016)(南京航空航天大学无人机研究院 南京 210016)

为了提高系统特征提取算法的计算效率、减少占用的存储空间和简化程序设计，该文基于Riemann流形上优化算法的几何框架，提出了改进的Stiefel流形上的梯度下降算法。根据不同要求采用不同的测地线计算公式，并使用多项式逼近测地线方程，同时采用了秦九韶-Horner多项式算法及线搜索、变步长的方法。以主分量分析问题为例，详细讨论了Stiefel流形上的梯度算法在其中的应用。理论分析和实验结果均表明，此方法可以在确保迭代矩阵列向量单位正交性的同时获得更好的计算效率和收敛速度，并且更容易实现。

Stiefel流形；特征提取；梯度算法；测地线；主分量分析

1 引言

系统特征信息分析方法包括主分量分析(Principal Component Analysis, PCA)、次分量分析(Minor Component Analysis, MCA)和独立分量分析(Independent Component Analysis, ICA)等，其广泛应用于数据压缩、波达方向估计、信号滤波等信号处理领域。近十年来，众多专家学者提出了各种算法。然而，现行的各种算法大都是基于欧氏空间的，这些学习算法并没有充分利用约束集为Stiefel流形这一事实，因而也就不能充分利用Stiefel流形的几何性质。另外，这类算法往往需要进行特征分解，而特征分解运算量大，算法复杂，工程难以实现。

本文首先详细讨论了Riemann流形上梯度算法，重点讨论了Stiefel流形上的梯度算法。其次，对测地线公式作了深入分析与比较，为了能够在工程实际中应用，作了较大改进，提出了改进的梯度下降算法M-GDM(Modified Gradient Descent Method)。最后，以主分量分析问题为例，详细讨论如何在Stiefel流形上应用梯度下降算法。

2 Riemann流形上的梯度算法

作为求解非线性最优化问题的新方法，基于流形的几何优化算法核心思想是把约束集视为高维空间中的曲面，也就是(微分)流形。当在流形上指定了一个Riemann度量(也就是在流形的每一点的切空间上指定一个对称、正定的2阶协变张量)后，成为Riemann流形。

测地线是Riemann几何中非常重要的概念，定义如下：

一方面，由于Riemann流形本质上是一种弯曲的空间，所以迭代估计应该沿着流形的测地线进行；另一方面，维Euclidean空间是一种曲率处处恒为0的特殊的Riemann流形，所以无约束最优化和约束最优化都可以统一成Riemann流形上的最优化。然而由于Euclidean空间中的直线就是测地线，所以无约束优化的搜索方向可以沿着空间中任何方向，而约束最优化的搜索方向则应沿着Riemann流形上测地线所对应的切方向。据此，可以解决梯度算法中的一个关键问题搜索方向，并可以得出Riemann流形上无约束优化和约束优化的梯度类算法的统一框架。

(2) 计算负梯度方向对应的测地线。因为Euclidean空间中测地线就是直线，所以对于无约束最优化，就是。然而对于约束最优化，则应先计算，然后把投影到流形在点处的切空间上。

在一定条件下，可以证明上面的梯度算法是收敛的。证明过程较长，可以参阅文献[8]。

3 Stiefel流形及其测地线方程

值得指出的是，Stiefel流形是紧致的，即参数的取值范围是一个有限闭集。关于这一点，可以简单的说明一下，设有，则有

(3)

Riemann流形上梯度下降算法的另一个核心问题测地线的计算。在微分流形与Riemann几何中测地线方程的推导往往采用内蕴的方式，测地线对应一组微分方程组的解，直接求解并应用到实际中有很大困难。然而Stiefel流形上的测地线却有相对简单的表达式，文献[10]给出了Stiefel流形上测地线的一种计算公式，以定理表述如下：

(5)

(7)

文献[11]同时也给出了相应的测地线逼近公式，但是需要矩阵求逆和矩阵乘方。

测地线计算公式(4)需要QR分解及矩阵指数运算，测地线计算公式(6)需要矩阵求逆及矩阵乘方运算，这两种方法不仅计算量大，而且占用较大的存储空间、编程复杂。为了减小计算量，同时简化程序设计，必须简化测地线的计算方法(当然必须尽可能地满足单位列正交性的约束条件，这是在流形上进行优化的根本目的)。

鉴于此，本文对上面两种算法中的矩阵指数运算作近似。考虑矩阵指数函数的Taylor展开式：

由于流形上指数映射往往限于局部，取值往往比较小(比如取0.01)，又由于Stiefel流形为紧致的，所以最终切向量中的元素取值较小，和中各个元素相乘后，再进行矩阵乘法运算，最终的矩阵元素取值就更小，略去这些项，误差会非常小，对正交性约束影响也自然非常小。

以上定性分析了误差较小的原因，下面进行定量分析，给出误差一个较好的上界。设截取项，表示矩阵范数，并令，则有

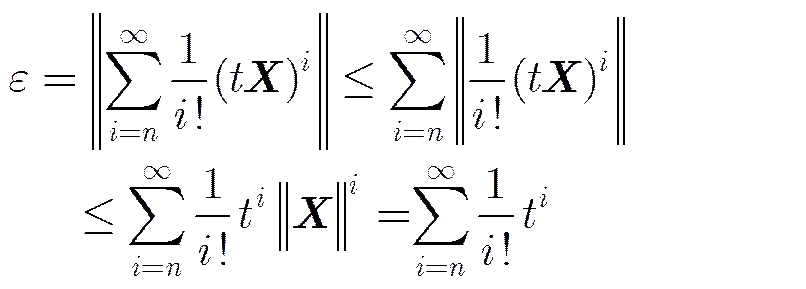
(10)

为了进一步减少计算量，对多项式运算采用秦九韶-Horner算法，即：

梯度算法的第3个关键问题是迭代步长的选取。迭代步长的选取本质上是一种“线搜索”或“1维搜索”技术，为了使算法具有更好的性能，应区分批处理和在线处理这两种不同的情形，并采用不用的策略，而以往大多数算法都忽略了这一重要问题。

对于批处理情形，此时相关矩阵已经比较好地估计出来(用时间平均取代统计平均)，一定程度上，此时已经是确定性的最优化问题，所以采用不精确线搜索技术Armijo准则。欧氏空间中，Armijo准则是指对于给定，令步长因子，其中为满足下列不等式的最小非负整数：

在一些信号处理领域，为了能够实时处理，必须采用在线处理的方式，由于此时相关矩阵的估计仅仅采用当前时刻的采样值，所以相关矩阵是非常不精确的和随机的。为了减小稳态误差、提高性能，应采用变步长的方法。变步长的方法较多，本文采用比较简单的变步长公式，其它的变步长方法可以参考自适应滤波相关的文献等。

4 Stiefel流形上的特征提取

定理2设Stiefel流形上1阶连续可微函数为,为Stiefel流形上的点。当把Stiefel流形嵌入到Euclidean空间后，在Euclidean空间中的梯度为，投影到流形上点处的切空间得，则和有关系：。

据此，由Riemann流形上梯度算法的一般框架，可以得出Stiefel流形上梯度算法的一般步骤：

必须指出的是，测地线计算公式的选择很重要，当待求的主分量数目较少时，应选用式(4)，否则应选用式(6)。

下面以PCA问题为例，讨论如何在Stiefel流形上应用梯度下降算法。PCA问题可以等价为Stiefel流形上非线性约束最优化问题：

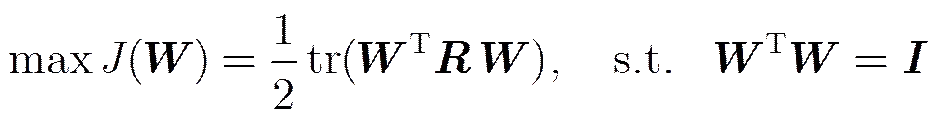
(16)

至于MCA和ICA等问题，只要知道代价函数，很容易依次类推。

5 数值仿真与结论

记文献[11,16]提出的算法为E-GDM(Exponential Gradient Descent Method)。

实验1 比较正交性。求5维随机向量的第1，第2主分量，分别设为和。理论上，和应相互正交，即。但是，采用多项式近似后，必然有误差，即，直接取绝对值作为正交性误差的度量，即。实验时随机选取的5 维随机向量的协方差矩阵为：

多项式取7项，步长参数取0.01，迭代100次，结果如图1。

从实验可以看出，用多项式近似和使用指数映射(exp)其性能是非常接近的，对正交性约束的影响极小，可以认为正交性得以保持。

实验2 比较运行时间。由于matalb中QR分解算法是用内嵌汇编实现的，为了便于比较，故使用C语言编程实现两种算法。多项式取7项，向量维数从40取到100，每次取10000个采样数据，E-GDM算法与M-GDM算法占用的时间比如图2。

可以看出时间比基本稳定在15左右，然而本文的算法简单、占用存储空间也小。

从实验可以看出，由于改进的算法采用了“线搜索”技术，收敛速度更快，不仅迭代步数变小，而且误差也更小。

6 结束语

如文中所指出，如果在高维数据(设为)中仅仅提取少量主分量(设为)，则应选用测地线计算公式(4)；当提取的主分量数接近或者当时，则应选用第2个测地线计算公式(6)。在独立分量分析问题中，几乎总是使用计算公式(6)。总而言之，应具体问题具体对待。

在Riemann流形(包括Stiefel流形)上发展其它类型的优化算法，并将其应用到信号处理中，以提高算法的效率，不仅是重要的思路，也是一个值得研究的方向。

图1 正交性误差比较

图2 E-GDM和M-GDM占用的时间比

图3 收敛速度性能曲线

[1] Kong X Y, Hu C H, and Han C Z. A dual purpose principal and minor subspace gradient flow[J]., 2012, 60(1): 197-201.

[2] Eldar Y C and Oppenheim A V. MMSE whitening and subspace whitening[J]., 2003, 49(7): 1846-1851.

[3] Chang D X, Feng D Z, and Zheng W X. A fast recursive total least squares algorithm for adaptive IIR filtering[J]., 2005, 53(3): 957-965.

[4] Ouyang S and Bao Z. Fast principal component extraction by a weighted information criterion[J]., 2002, 50(8): 1994-2002.

[5] Moller R and Konies A. Coupled principal component analysis[J].2004, 15(1): 214-222.

[6] Rapcsak T. On minimization on Stiefel manifold[J]., 2002, 143(2): 365-376.

[7] Jurgen J. Riemannian Geometry and Geometric Analysis[M]. Berlin Heidelberg, NY, US, Springer, 2005: 13-20.

[8] Ferrira O P and Oliveira P R. Sub gradient algorithm on Riemannian manifolds[J]., 1998, 97(1): 93-104.

[9] Yang Y. Global convergent optimization algorithm on Riemannian manifold: uniform framework for unconstrained and constrained optimization[J]., 2007, 132(2): 245-265.

[10] Edelman A, Arias T, and Smith S. The geometry of algorithm with orthogonality constraints[J]., 1998, 20(2): 302-353.

[11] Nishimor Y and Akaho S. Learning algorithm utilizing quasi- geodesic flows on the Stiefel manifold[J]., 2005, 67: 106-135.

[12] 徐树方, 钱江. 矩阵计算六讲[M]. 北京: 高等教育出版社, 2011: 70-71.

Xu Shu-fang and Qian Jiang. Six Lectures on Matrix Computation[M]. Beijing: Higher Education Press, 2011: 70-71.

[13] 黄建国, 孙连山, 叶中行. 黎曼流形上带Armijo准则步长准则优化算法[J]. 上海交通大学学报, 2002, 36(2): 267-271.

Huang J G, Sun L S, and Ye Z X. Optimization algorithm with Armijo rule on Riemann manifold[J]., 2002, 36(2): 267-271.

[14] 张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 2012: 199-200.

Zhang X D. Modern Signal Processing[M]. Beijing: Tsinghua University Press, 2012: 199-200.

[15] Yang H H. Series updating rule for blind separation derived from scoring[J]., 1999, 47: 2279-2285.

[16] 段玲, 黄建国. 主成分分析的一个黎曼几何随机算法[J]. 上海交通大学学报, 2004, 38(1): 71-74.

Duan L and Huang J G. A Riemannian geometry underlying stochastic algorithm for adaptive principal component analysis[J]., 2004, 38(1): 71-74.

Gradient Algorithm on Stiefel Manifold and Application in Feature Extraction

Zhang Jian-junCao JieWang Yuan-yuan

(College of Electronic and Information Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing210016, China)(Unmanned Aerial Vehicle Research Department, Nanjing University of Aeronautics and Astronautics, Nanjing210016, China)

To improve the computational efficiency of system feature extraction, reduce the occupied memory space, and simplify the program design, a modified gradient descent method on Stiefel manifold is proposed based on the optimization algorithm of geometry frame on the Riemann manifold. Different geodesic calculation formulas are used for different scenarios. A polynomial is also used to lie close to the geodesic equations. JiuZhaoQin-Horner polynomial algorithm and the strategies of line-searching technique and change of the step size of iteration are also adopted. The gradient descent algorithm on Stiefel manifold applied in Principal Component Analysis (PCA) is discussed in detail as an example of system feature extraction. Theoretical analysis and simulation experiments show that the new method can achieve superior performance in both the convergence rate and calculation efficiency while ensuring the unitary column orthogonality. In addition, it is easier to implement by software or hardware.

Stiefel manifold; Feature extraction; Gradient algorithm; Geodesic; Principal component analysis

TP391

A

2095-283X(2013)03-0309-05

10.3724/SP.J.1300.2013.13048

2013-05-22收到，2013-08-30改回；2013-09-03网络优先出版

国家自然科学基金(61106018)资助课题

章建军 hblyup@163.com

章建军(1988-)，男，江苏南京，硕士研究生，主要研究方向为优化算法与盲信号处理。

E-mail: hblyup@163.com

曹 杰(1963-)，男，研究员，研究方向为信号处理、数字图像处理。

王源源(1988-)，女，江苏镇江，硕士研究生，主要研究方向为数据压缩。