极化敏感阵列斜投影滤波性能分析

田 静* 廖桂生 杨志伟



极化敏感阵列斜投影滤波性能分析

田 静廖桂生 杨志伟

(西安电子科技大学雷达信号处理重点实验室 西安 710071)

该文研究了极化敏感阵列采用斜投影滤波和正交投影滤波的输出信干噪比(SINR)特性。推导获得了斜投影滤波与正交投影滤波在理想情况和存在阵列误差时的输出SINR计算式：理想情况下输出SINR是信噪比(SNR)、目标与干扰的空域和极化域匹配系数的函数；存在阵列误差情况时输出SINR受信噪比，干噪比(INR)、目标与干扰的空域-极化域匹配系数及误差扰动量共同影响。分析表明，相比正交投影滤波而言，斜投影滤波的输出SINR没有改善，也不能提高误差稳健性，它们均低于最优输出SINR；正交投影与斜投影输出SINR相同的成因并不一样，正交投影滤波改变了目标的幅相特性，滤波后目标有损失；斜投影滤波改变了输出噪声的空域-极化域特性，放大了输出噪声的功率。最后通过仿真实验验证了理论分析的正确性。

极化敏感阵列；斜投影滤波；正交投影滤波；阵列误差

1 引言

极化敏感阵列不仅可以实现空域-极化域联合滤波，改善传统空域滤波的效果，而且可以获取更完整的目标信息，因此受到了越来越多的重视。上世纪80年代，R. T. Compton最早研究了简单极化敏感阵列的滤波性能。文献[4,5]分别讨论了完全极化干扰与相关极化干扰情况下极化敏感阵列的滤波性能。文献[6]进一步分析了阵列误差对极化敏感阵列滤波性能的影响。遗憾的是，这些研究直接利用传统滤波方法处理极化敏感阵列信号，滤波后目标信号的幅相特性和矢量性被破坏，从而限制了其在相参系统和极化目标识别等方面的应用。

文献[7,8]提出利用斜投影实现极化敏感阵列的滤波，并指出斜投影滤波在完全抑制掉干扰的同时不会改变目标的矢量性，在矢量信号处理方面具有强大的应用潜力。文献[9]将斜投影应用到移动通信的极化滤波上，在保持目标幅相特性的同时完全抑制掉了共信道干扰。文献[10,11] 在干扰信息未知的情况下利用斜投影方法实现了极化敏感阵列滤波，提高了其滤波精度。文献[12,13]将斜投影应用于多维域联合滤波中，进一步扩展了斜投影的应用范围。但目前并没有关于极化敏感阵列斜投影滤波性能的完整分析结果发表，对于斜投影是否可以提高滤波性能、在误差情况下的性能损失情况尚未见报道。

本文重点对比分析了极化敏感阵列斜投影滤波与正交投影滤波输出SINR (Signal-to-Interference- and-Noise Ratio)性能，在极化敏感阵列信号接收模型基础上，推导获得斜投影滤波与正交投影滤波在理想情况和存在阵列误差时的输出SINR计算式，理想情况下输出SINR是信噪比、目标与干扰的空域-极化域匹配系数的函数，存在阵列误差情况时输出SINR受信噪比(SINR)、干噪比(Interference-to- Noise Ratio, INR)、目标与干扰的空域-极化域匹配系数及误差扰动量共同影响。相比正交投影滤波而言，斜投影滤波的输出SINR没有改善，它们均低于最大SINR准则获得的输出SINR。进一步分析表明，正交投影与斜投影输出SINR相同的成因并不一样，正交投影滤波改变了目标的幅相特性，滤波后目标有损失；斜投影滤波改变了输出噪声的空域-极化域特性，放大了输出噪声的功率。最后通过仿真实验验证了理论分析的正确性。

2 接收信号模型

极化敏感阵列由在空间按照一定方式放置的多个极化敏感阵元构成，它能同时获取电磁波的极化信息和空间信息。本文以个正交偶极子天线组成的均匀线阵为例给出极化敏感阵列的接收信号模型，阵列结构如图1所示。正交偶极子天线分别沿轴和轴方向放置，各阵元沿轴均匀排列，间距为。

不失一般性，假定有1个目标和1个干扰从远场入射到极化敏感阵列上，目标方向为，干扰方向为。则第组天线接收信号为：

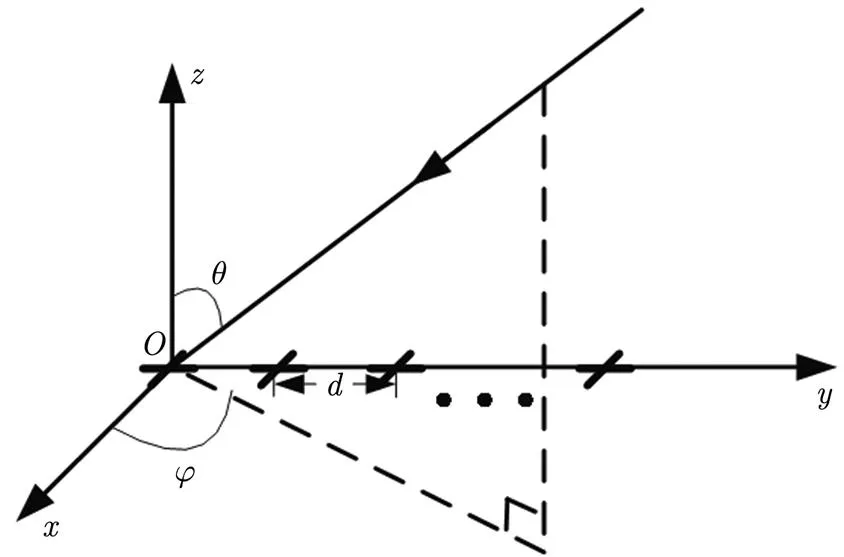
图1 极化敏感阵列

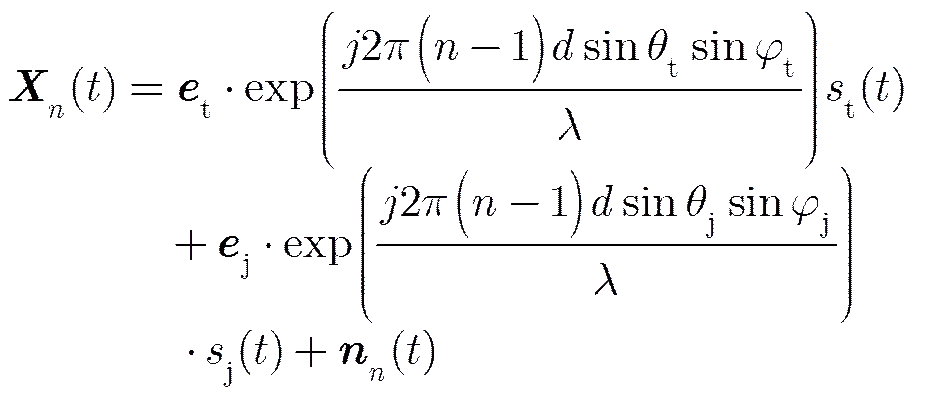
其中

和

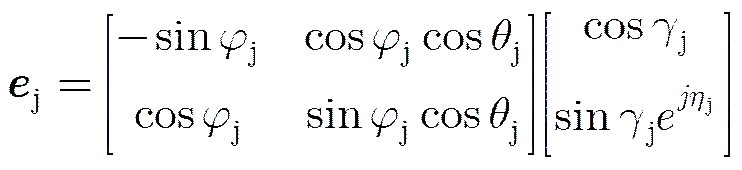
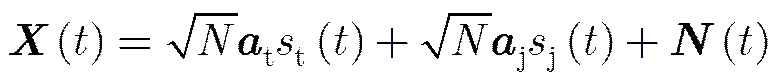
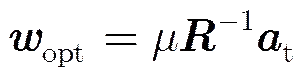
式中为任意非零常数，为噪声协方差矩阵与干扰协方差矩阵之和，分别表示噪声功率和干扰功率。此时阵列输出最优为：

(4)

由矩阵求逆引理得，式(4)可展开为如下形式：

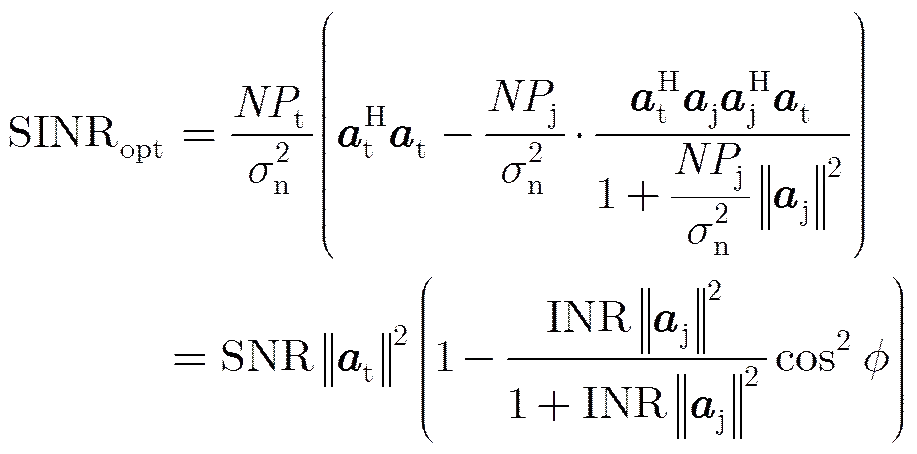
3 理想情况下滤波性能分析

干扰信息已知和未知时均可实现斜投影极化滤波，但正交投影滤波需要知道目标与干扰的空域-极化域联合导向矢量，因此需要提前估计目标与干扰的方位角与极化状态，具体的估计方法详见文献[14]，为统一对比两种投影算法的性能，这里我们假设目标与干扰的方向与极化状态已经精确得到。下面利用第2节建立的极化敏感阵列接收信号模型分析斜投影滤波与正交投影滤波对目标、干扰及噪声的幅相特性和功率的影响。

3.1 斜投影滤波

极化敏感阵列斜投影滤波的处理器结构如图2所示，其中斜投影矩阵是利用目标与干扰的空域-极化域联合导向矢量构造的。这里以式(2)给出的目标与干扰导向矢量构造如下斜投影矩阵：

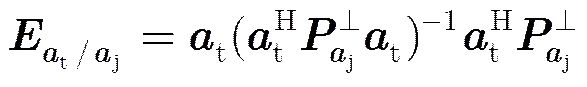
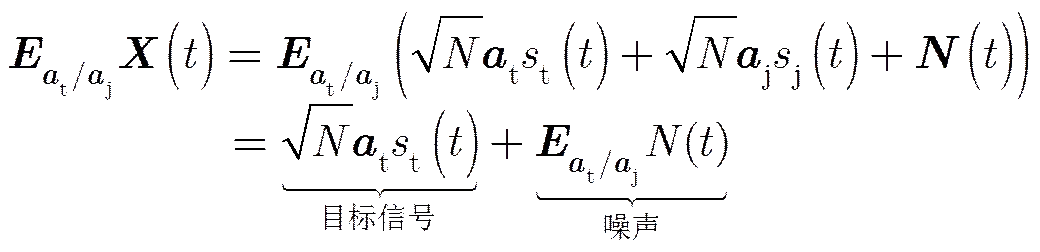
我们发现接收信号通过斜投影矩阵后干扰被完全滤除而目标幅相特性仍保持不变，此时对输出信号进行空域匹配滤波 (如图(2)所示，其中)，便可得到矢量信号的两个正交分量。

图 2 极化敏感阵列斜投影滤波处理器结构

Fig. 2 The architecture of oblique projection filtering on polarization sensitive array

为直观了解斜投影滤波对噪声的影响，对式(6)进行奇异值分解：

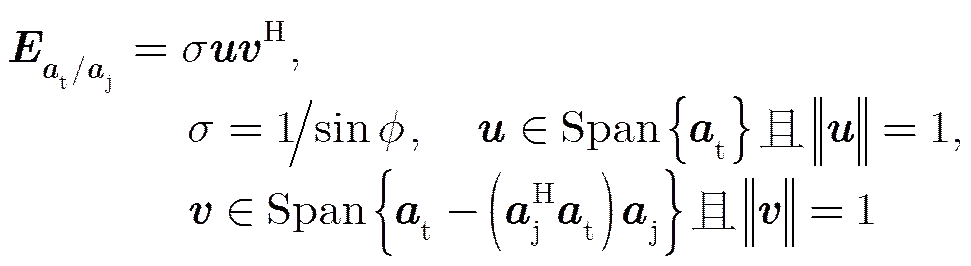
由上式可看出干扰信号正交补空间与目标信号空间的交空间构成了斜投影矩阵所在的空间，而正交投影矩阵所在的空间为干扰信号的正交补空间，这是斜投影矩阵与正交投影矩阵的根本区别。

将式(8)代入式(7)中，输出信号可表示为：

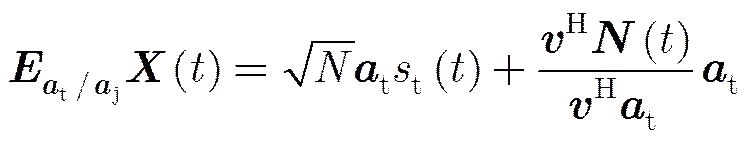
斜投影滤波后噪声在空域由白噪声变为低维色噪声，并且由部分极化波变为完全极化波，即噪声特性发生了改变。由于它与目标具有相同的导向矢量，因此两者在空域不可区分。此时目标与输出噪声的功率直接由式(9)计算得到：

（10）

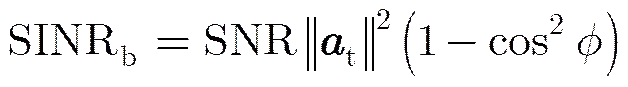
最后考虑斜投影滤波的一种特殊情况，当目标信号空间与干扰信号空间正交时，式(6)变为如下形式：

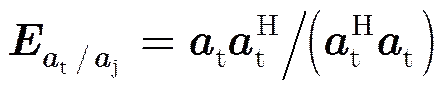
3.2 正交投影滤波

正交投影滤波的基本思想是在完全消除干扰的条件下使得输出信噪比最大，可描述为如下优化问题：

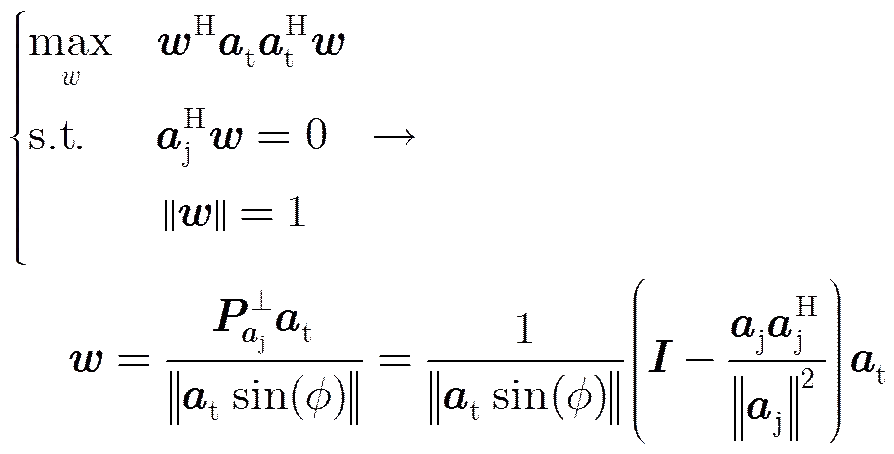
联合式(2)与式(13)可得信号经过正交投影滤波后变为：

（14）

正交投影滤波也可完全滤除掉干扰，但滤波后目标幅度也出现了损失，损失量的大小与目标和干扰导向矢量夹角余弦有关。此时目标和输出噪声的功率由式(14)计算得到：

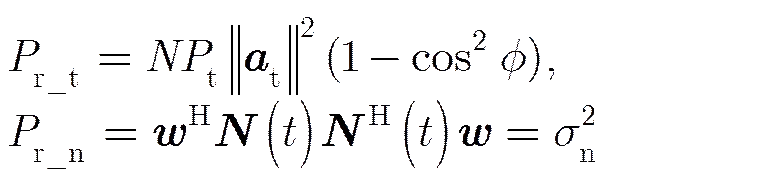
(16)

由式(15)可看出，正交投影滤波未改变噪声的功率但目标功率损失了倍。

前面的分析已指出正交投影滤波与斜投影滤波均可完全滤除干扰，但是正交投影滤波会产生目标损失；斜投影滤波则保持了目标的幅相特性与极化特性，在信号匹配和极化识别等应用方面，斜投影优于正交投影。然而对比式(11)和式(16)我们发现，相对正交投影滤波而言，斜投影滤波的输出并没有改善(文献[17]在对比普通阵列斜投影滤波和正交投影滤波时也得到了类似的结论)，且改变了滤波后的噪声特性。因此，在目标能量检测应用方面，正交投影滤波优于斜投影滤波。对比式(5)和式(16)看到斜投影滤波与正交投影滤波并不是最优滤波，干噪比较低时斜投影滤波与正交投影滤波的干扰抑制性能低于最优输出，干噪比较高时斜投影滤波与正交投影滤波的输出近似等于最优输出。

4 误差情况下滤波性能分析

实际工程中，幅相误差、位置误差及耦合误差会不可避免地存在于极化敏感阵列中。因此，有必要分析存在上述误差时两种投影滤波方法的稳健性。针对幅相误差和位置误差，首先给出存在误差时导向矢量的自相关矩阵，然后利用该自相关矩阵推导两种投影滤波方法的输出，并进行对比分析。由于耦合误差使得导向矢量变得复杂，缺少规律性，本文采用数值仿真实验分析其对两种投影滤波方法输出的影响。

4.1 阵列误差模型

(1) 幅相误差

极化敏感阵列中存在幅相误差时，接收信号的导向矢量可表示如下：

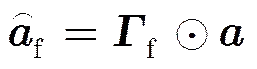
幅相误差下导向矢量自相关矩阵为：

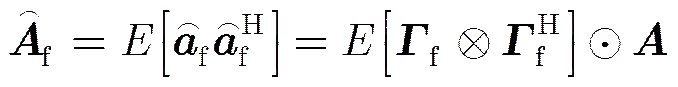
(19)

其中

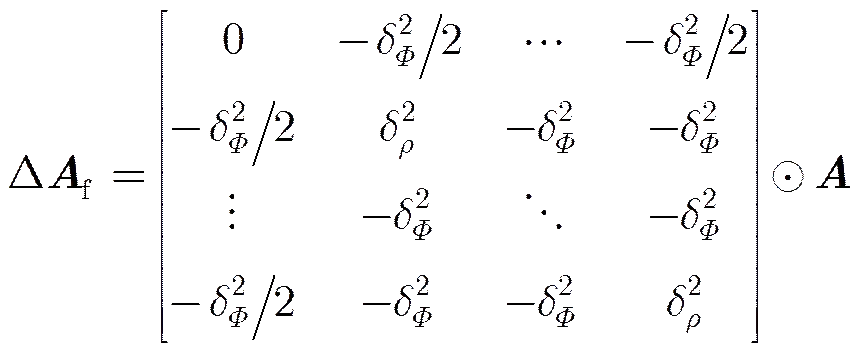
(2)位置误差

本文以一台1.2 kW某型号无人机用永磁无刷直流舵电机为例，阐述了传统作圆求点制电枢冲片梯形槽法；然后对比理想梯形槽找出差异，经分析差异对电机槽满率、热负荷、磁密、负载效率等性能的影响，得出以下结论：

位置误差下导向矢量自相关矩阵为：

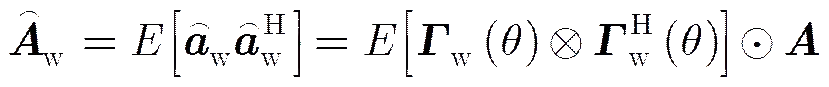
(22)

其中

(3)耦合误差

文献[6]指出极化敏感阵列中的互耦误差可表示为阵元极化互耦误差与阵列孔径互耦误差的Kronecker积。对于均匀线阵，假设仅有相邻偶极子之间存在互耦影响时，带有耦合误差的导向矢量可表示如下：

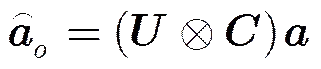
式中

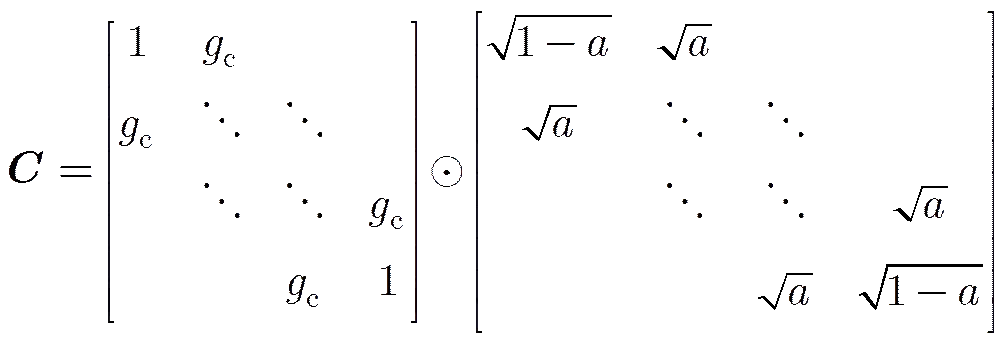
带有耦合误差的导向矢量式(20)表达式较为复杂，很难得到类似于式(17)的自相关矩。这里利用数值仿真实验对比存在耦合误差时两种投影滤波方法的输出。

4.2 滤波性能分析

幅相误差下的导向矢量自相关矩阵式(19)与位置误差下的导向矢量自相关矩阵式(22)均可表示为理想情况下的自相关矩阵与扰动矩阵之和。为避免重复性分析，下面采用统一的误差形式表示幅相误差和位置误差，并以阵列误差代指幅相误差或位置误差：

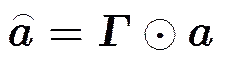
(25)

阵列误差下的接收信号可表示为：

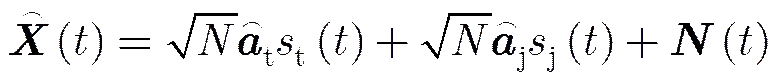
(1)斜投影滤波

联合式(8)与式(26)进行斜投影滤波后输出信号为：

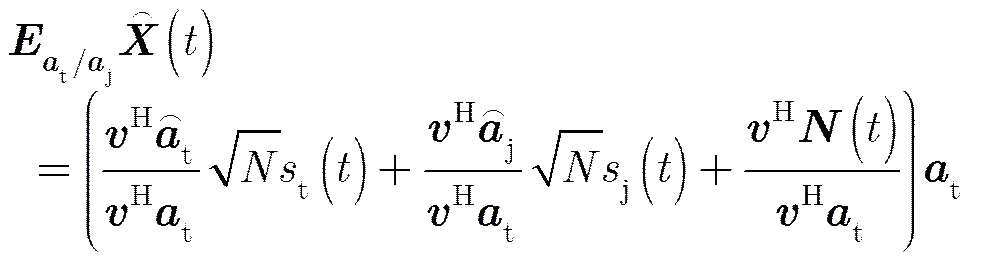
由于存在阵列误差斜投影滤波后存在残余干扰并且目标的幅度与相位均受误差影响产生扰动，而输出噪声特性与理想情况是一致的。滤波后目标，剩余干扰及噪声具有相同的空域-极化域导向矢量，因此滤波后3种信号在空域不可区分。

由式(25)和式(27)推得斜投影滤波后目标，剩余干扰及噪声的功率分别为：

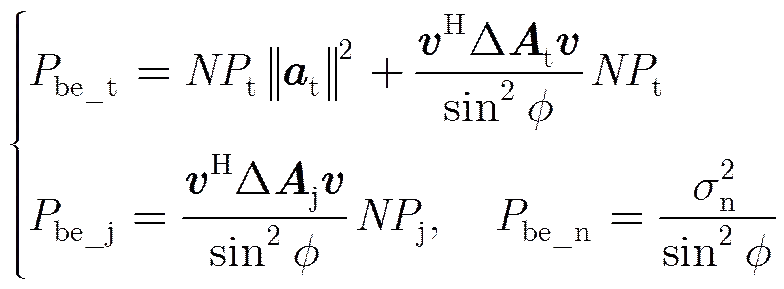
(29)

(2) 正交投影滤波

联合式(13)与式(26)进行正交投影滤波后输出信号为：

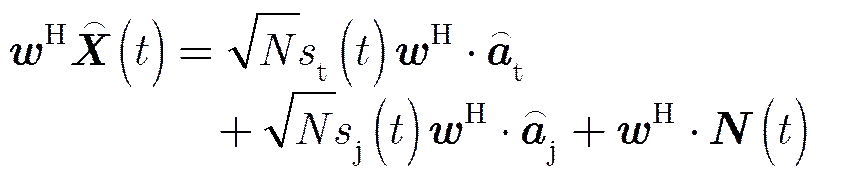
由于存在阵列误差正交投影滤波后仍存在残余干扰，目标的相位受误差影响产生扰动并且幅度的损失情况也与阵列误差有关。

由式(8)，式(25)和式(30)推得正交投影滤波后目标，剩余干扰及噪声的功率分别为：

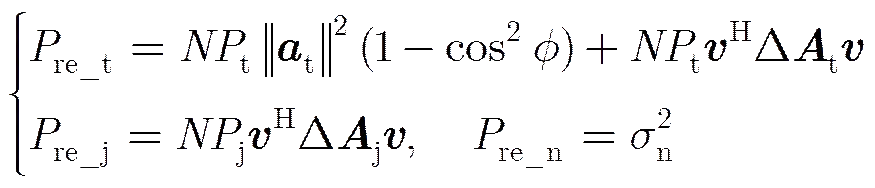
(32)

阵列误差情况下斜投影滤波与正交投影滤波的滤波性能相对于理想情况有一定损失，两种滤波方法不能完全抑制掉干扰并且斜投影滤波不再具有保持目标幅相特性的特点。比较式(29)和式(32)发现斜投影滤波与子空间投影滤波输出依旧相等，因此两者具有相同的阵列误差稳健性。

5 仿真实验

为验证理论分析的正确性，以图1的阵列结构进行仿真实验，实验中设定阵元数，阵元间距，单个接收通道的噪声方差，信噪比及干噪比，目标与干扰的方位角，极化角。

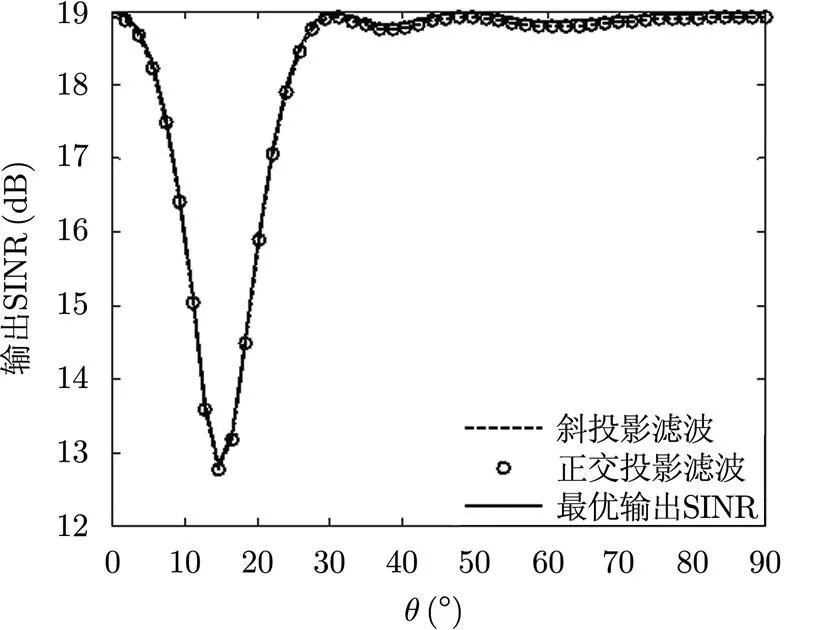
图3 输出SINR随干扰俯仰角变化曲线

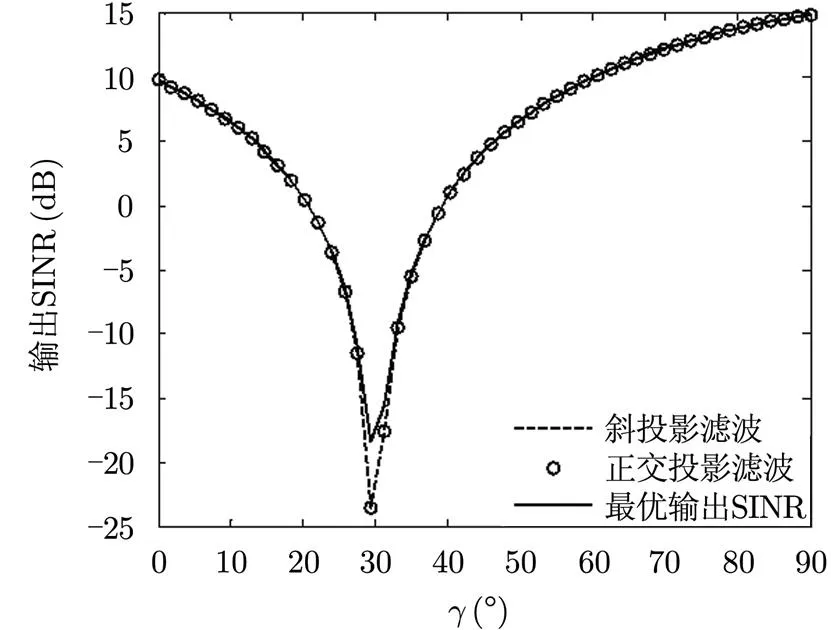
图4 输出SINR随干扰极化状态角变化曲线

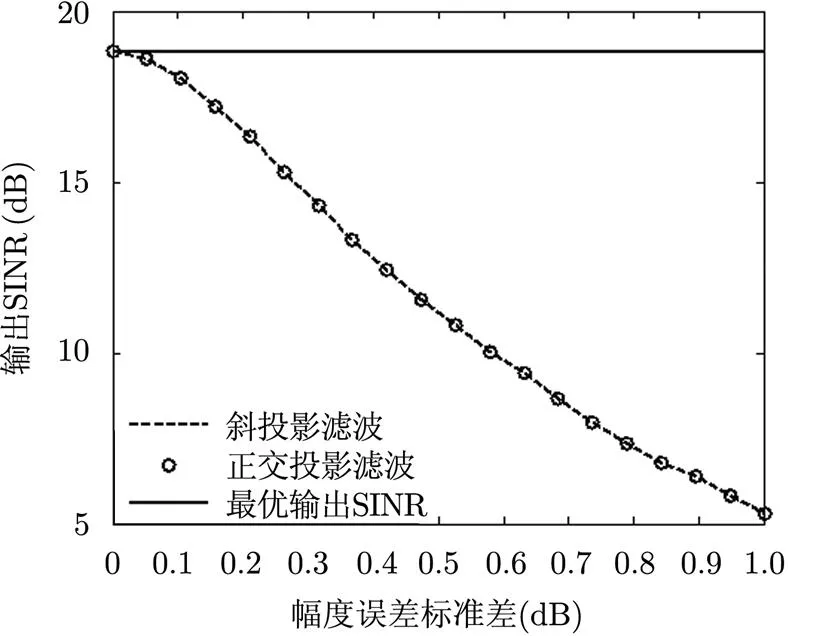
图5 输出SINR随幅度误差变化曲线

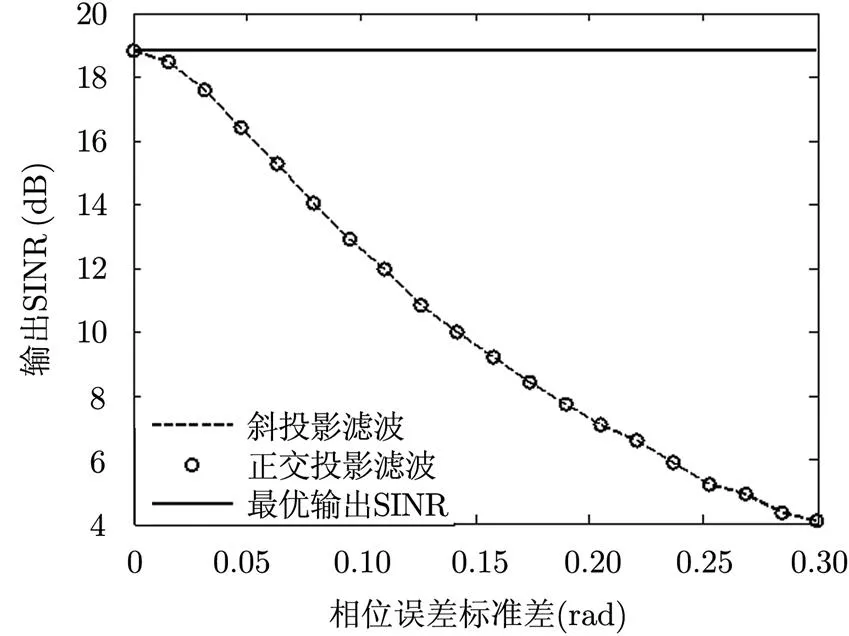
图6 输出SINR随相位误差变化曲线

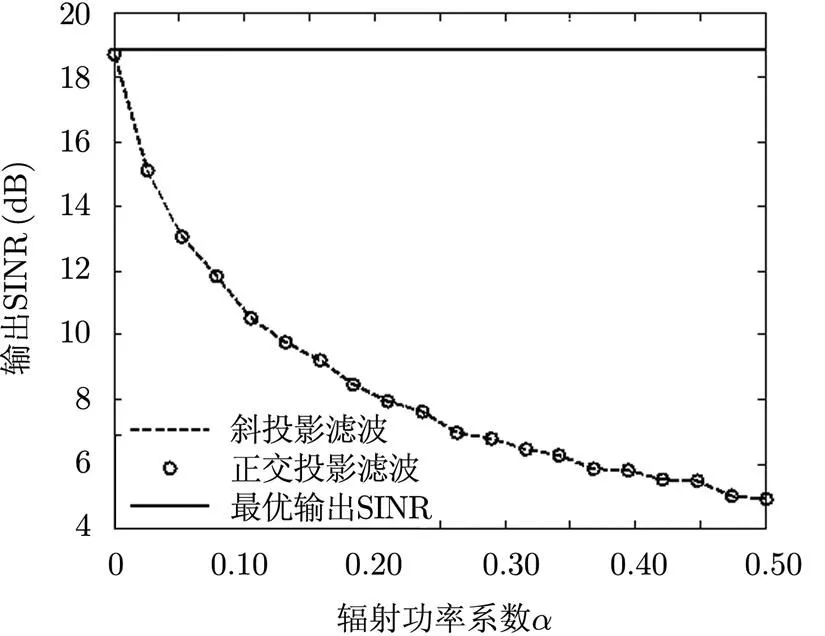
图7 输出SINR随耦合误差变化曲线

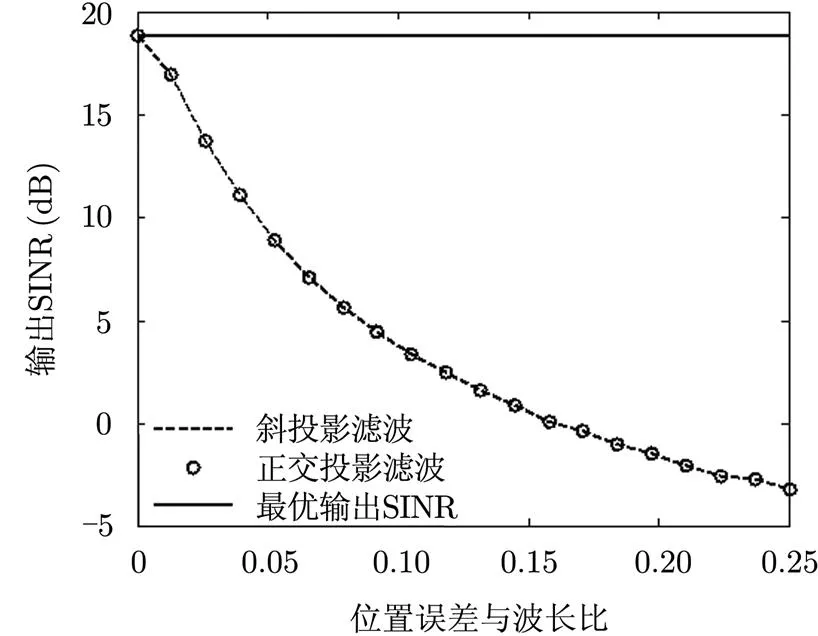
图8 输出SINR随位置误差变化曲线

6 结论

本文针对极化敏感阵列对比分析了斜投影和正交投影滤波性能。首先推导获得理想情况下斜投影与正交投影滤波输出的计算式，结果表明斜投影与正交投影的滤波效果有很大差异斜投影滤波放大了噪声功率而正交投影滤波则造成目标功率损失，但是斜投影与正交投影滤波却具有相同的输出。其次通过建立存在阵列误差时斜投影与正交投影滤波模型，进一步分析了误差情况下斜投影与正交投影的滤波效果，结果表明斜投影与正交投影滤波具有相同的误差稳健性。仿真结果验证了理论分析的正确性。

[1] Compton R T, Jr. On the performance of a polarization sensitive adaptive array[J]., 1981, 29(5): 718-725.

[2] Compton R T, Jr. The tri-pole antenna: an adaptive array with full polarization flexibility[J]., 1981, 29(6): 944-952.

[3] Compton R T, Jr. The performance of a tri-pole adaptive array against cross-polarized jamming[J]., 1983, 31(4): 682-685.

[4] 徐振海, 王雪松, 肖顺平, 等. 极化敏感阵列滤波性能分析: 完全极化情形[J]. 电子学报, 2004, 32(8): 1310-1313.

Xu Zhen-hai, Wang Xue-song, Xiao Shun-ping,.. Filtering performance of polarization sensitive array: completely polarized case[J]., 2004, 32(8): 1310-1313.

[5] 徐振海, 王雪松, 肖顺平, 等. 极化敏感阵列滤波性能分析: 相关干扰情形[J]. 通信学报, 2004, 25(10): 8-15.

Xu Zhen-hai, Wang Xue-song, Xiao Shun-ping,.. Filtering performance of polarization sensitive array: correlated interference case[J]., 2004, 25(10): 8-15.

[6] 刘勇, 徐振海, 肖顺平. 阵列互耦对极化敏感阵列滤波性能的影响[J]. 电子学报, 2006, 34(12): 2303-2306.

Liu Yong, Xu Zhen-hai, and Xiao Shun-ping. The effect of array mutual coupling on filtering performance of polarization sensitive array[J]., 2006, 34(12): 2303-2306.

[7] Mao X.-P, Liu A.-J, and Hou H.-J,.. Oblique projection polarization filtering for interference suppression in high-frequency surface wave radar[J].,&, 2012, 6(2): 71-80.

[8] 毛兴鹏, 刘爱军, 邓维波, 等. 斜投影极化滤波器[J]. 电子学报, 2010, 38(9): 2003-2008.

Mao Xing-peng, Liu Ai-jun, Deng Wei-bo,.. An oblique projecting polarization filter[J]., 2010, 38(9): 2003-2008.

[9] Cao Bin, Yu Jia, Wang Ye,.. Enabling polarization filtering in wireless communications: models, algorithms, and characteristics[J]., 2013, 7(3): 247-254.

[10] 张钦宇, 曹斌, 王健, 等. 基于斜投影的极化滤波技术[J]. 中国科学: 信息科学, 2010, 40(1): 91-100.

Zhang Qin-yu, Cao Bin, Wang Jian,.. Polarization filtering technique based on oblique projection[J]., 2010, 40(1): 91-100.

[11] Cao Bin, Zhang Qin-yu, Liang Dong,.. Blind adaptive polarization filtering based on oblique projection[C]. IEEE International Conference on Communications (ICC), Cape Town, South Africa, May 2010: 1-5.

[12] Hong Hong, Mao Xing-peng, Hu Cui,.. A multi-domain collaborative filter for HFSWR based on oblique projection[C]. IEEE Radar Conference (RADAR),Atlanta, GA, May 2012: 0907-0912.

[13] 刘爱军, 宋立众, 王季刚, 等. 斜投影三维极化滤波[J]. 哈尔滨工业大学学报, 2012, 44(3): 75-80.

Liu Ai-jun, Song Li-zhong, Wang Ji-gang,.. Three- dimensions polarization filtering based on oblique projection[J]., 2012, 44(3): 75-80.

[14] 庄钊文. 极化敏感阵列信号处理[M]. 北京: 国防工业出版社, 2006: 204-209.

Zhuang Zhao-wen. Signal Processing of Polarization Sensitive Array[M]. Beijing: National Deference Industry Press, 2006: 204-209.

[15] Behrens R T and Scharf L L. Signal processing applications of oblique projection operators[J]., 1994, 42(6): 1413-1424.

[16] 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004: 687-696.

Zhang Xian-da. Matrix Analysis and Applications[M]. Beijing: Tsinghua University Press, 2004: 687-696.

[17] Hellbourg G, Weber R, Capdessus C,.. Oblique projection beamforming for RFI mitigation in radio astronomy[C]. IEEE Statistical Signal Processing Workshop (SSP), Ann Arbor, MI, Aug. 2012: 93-96.

[18] Weiss A J and Friedlander B. Array shape calibration using sources in unknown locations—a maximum likelihood approach[J].,, 1989, 37(12): 1958-1966.

Performance Analysis of Oblique Projection Filtering Based on Polarization Sensitive Array

Tian Jing Liao Gui-sheng Yang Zhi-wei

(National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China)

The output Signal-to-Interference-and-Noise Ratio (SINR) of oblique projection and orthogonal projection filtering based on a polarization sensitive array is investigated. The output SINR formulae of the oblique projection and orthogonal projection filtering under both the ideal and array error conditions are derived. Under ideal conditions, the output SINR is a function of the spatial and polarized matching coefficient between the signal and interference whereas, under the array error condition, it is a function of the Interference-to-Noise Ratio (INR) and the perturbation momentum. The oblique projection filtering obtains the same output SINR as the orthogonal projection filtering under both conditions, but the output SINR of the maximum SINR principle filtering is the best. Further analysis shows that the oblique projection distorts the spatial and polarized properties of noise filtering while maintaining the amplitude and phase properties of the output signal, which are distorted in orthogonal filtering. The simulation results attest the reasonability of the analysis in this paper.

Polarization sensitive array; Oblique projection filtering; Orthogonal projection filtering; Array errors

TN911.7

A

2095-283X(2013)03-0284-08

10.3724/SP.J.1300.2013.13043

2013-04-23收到，2013-06-20改回；2013-06-28网络优先出版

国家自然科学基金(60901066), 预研基金(9140xxx0104)和中央高校基本科研业务费专项资金(K5051302007)资助课题

田静 j_jtian@126.com

田 静(1988-)，女，籍贯山东，西安电子科技大学硕士研究生，研究方向为极化敏感阵列信号处理。

E-mail: j_jtian @126.com.cn

廖桂生(1963-)，男，生于广西桂林。现为西安电子科技大学雷达信号处理重点实验室教授，博士生导师，教育部长江学者特聘教授和创新团队学术带头人，中国电子学会高级会员，IEEE会员。主持和承担了国防973项目课题、国家“863”高技术项目、国防科技预研、国家自然科学基金等科研任务，其中获省部级科技进步奖一等奖1项、二等奖2项、三等奖1项。1999年获教育部跨世纪优秀人才基金，2004年入选国家人事部颁发的首批“新世纪百千万人才工程国家级人选”，2008年获国家杰出青年科学基金。在国内外发表学术论文160余篇。现主要从事雷达探测系统信号处理、空时自适应处理、天基预警和阵列信号处理等研究。

E-mail: gsliao@xidian.edu.cn

杨志伟(1980-)，男，博士，生于四川南充。现为西安电子科技大学雷达信号处理国防科技重点实验室副教授，中国电子学会会员。主持了国家自然科学基金、国防预研基金、博士点基金和中央高校基本科研业务费等科研任务。主要从事阵列信号处理、空时极化自适应处理、地面运动目标检测和天基预警领域研究。

E-mail: yangzw@mail.xidian.edu.cn