A Novel Phase Compensation Method for ISAR Imaging in Wideband Radar

Chen Zeng-ping Zhang Wei-cheng Lin Qian-qiang*



A Novel Phase Compensation Method for ISAR Imaging in Wideband Radar

Chen Zeng-ping Zhang Wei-cheng Lin Qian-qiang

(ATR Key Lab, National University of Defense Technology, Changsha 410073, China)

This paper is proposed to eliminate the negative influence of the Rotational Phase Component (RPC) on the performance of the Doppler Centroid Tracking (DCT) phase compensation method. Firstly, the coherent property between adjacent echo pulses sampled directly in Intermediate Frequency (IF) is analyzed in the paper. Then a coherent phase compensation method is developed to improve the Translational Phase Component (TPC) estimation accuracy of DCT. Compared to the Modified DCT (MDCT) algorithm, the proposed method achieves better phase compensation performance. Experimental results prove the effectiveness and efficiency of the proposed strategy.

Wideband radar; Phase compensation; Direct Intermediate Frequency (IF) sampling; Curve fitting

1 Introduction

Inverse Synthetic Aperture Radar (ISAR) can obtain the 2-D images of moving targets (such as aircraft, ship, satellite,.), and improve the target recognition performance. Generally, ISAR aims at non-cooperative targets, this puts forward high request to motion compensation. The non- cooperative motion of radar target can be decomposed into rotational component and translational component. The rotational component is beneficial to ISAR imaging while the effects of translational component is just the opposite. Among them, the proceeding of eliminate the influence of translational component on echo envelope is called envelop alignment, and proceeding of eliminate the influence of rotational component on echo phase is called phase compensation. ISAR imaging raises a high demand on the latter. Therefore, improving precision of phase compensation plays an important role in improving the quality of ISAR imaging. Centring on this, domestic and foreign scholars carried out many related researches for a long time and achieved a lot of fruits. All of them can be classified into two kinds: one is parameterization method and the other is non-parameterization method. Among these numerous methods, Doppler Centroid Tracking (DCT) algorithm is adopted widely. DCT algorithm is the optimal one based on maximum likelihood criterion and can reduce the tracking loss induced by scintillation and obscuring while tracking the whole object instead of whichever scattering point. Also, it has fast calculation speed and is beneficial to real-time imaging. How- ever, the DCT algorithm has poor Translational Phase Component (TPC) estimation accuracy because of the Rotational Phase Component (RPC). The Modified DCT (MDCT) algorithm eliminates the negative influence of the RPC on the estimation accuracy of the TPC by circular shifting, windowing and iteration steps. Generally speaking, we need 8 to 10 times of iteration before obtaining good compensation performance. Consequently, the heavy computation load induced by times of iteration makes the MDCT method hard to be applied in engineering.

With the development of Analog-to-Digital Converter (ADC), direct Intermediate Frequency (IF) sampling for wideband radar comes true and is used widely in applications. Compared to STRETCH processing, direct IF sampling raises a high demand on sampling frequency. But it also brings obvious advantages. One of them is coherent property of echo pulses. Coherent property between echo pulses plays an important role in ISAR imaging. In this paper, we explore improving the translational component estimation accuracy of DCT with simpler operation by adopting the coherent property.

The remainder of this paper is organized as follows. In Section 2, the DCT algorithm is briefly introduced, as well as its limitation. Further, we analysis the coherent property of echo signal sampled directly in IF, and place an emphasis on the novel phase compensation method in Section 3. Experimental verification and conclusions are respectively given in Sections 4 and 5.

2 DCT Algorithm and Its Limitation

DCT algorithm is the embodiment of target centroid tracking method proposed firstly by Prichet. It tracks the target centroid and force the average Doppler to be zero. Its concrete implementation steps can be described as follows: After envelope alignment, calculate the weighted mean of adjacent echoes phase difference complex exponential function on weighted amplitude. In other words, obtain the Doppler centroid phase difference complex exponential functionas follows:

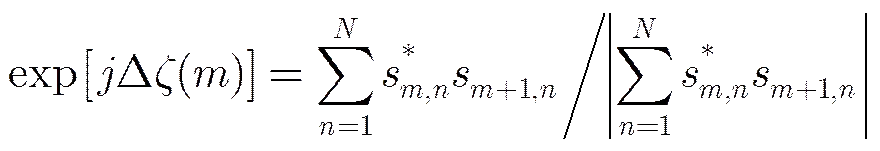
where=1, 2, … is the frame serial number,andare the sub-echoes of range bin n in the adjacent echoes (Frameand Frame+1),stands for the phase difference of adjacent echoes. This is the Doppler phase induced by envelope motion. Obtain the adjacent envelopes phase difference successively and establish Doppler centroid phase difference function. Calibrating the phase of all range bins using this function, we can complete the phase compensation. But the rotational component of target motion may reduce the translational phase estimation accuracy of DCT method. Ref. [4] proposed the MDCT algorithm which solves this problem based on circle shift operation. Unfortunately, the multiple iterations induce heavy computation load. To solve this problem, we improve the estimation accuracy of DCT method by adopting the coherent property of echo pulses.

3 Phase Compensation Method Based on the Coherent Property of Echo Pulses

3.1 Phase property of STRETCH method

It is assumed that the carrier frequency is,is the pulse duration,is time variable, andis the chirp rate. The amplitude of the Linear Frequency Modulation (LFM) signal is set to 1 for the convenience of analyzing. For STRETCH processing, the digital echo signals can be express in frequency domain as:

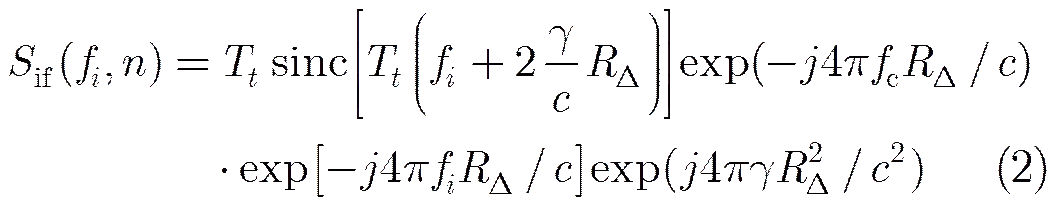
whereis the velocity of light,,is the distance between the target and radar, andis the reference distance. The second exponential term is Residual Video Phase (RVP) term, and the third exponential term is the envelop “sideling” term when. This two exponential phase term can be eliminated by phase compensation at the envelope peak point when. The first phase term is the echo pulse phase brought by translational motion:

(3)

As is shown in Eq. (3), the phase of STRETCH processing echo pulse is related to the radial distanceand the reference distance.is closely related to the time-delay of the narrowband echo, which is not precise enough. So the phase term in Eq. (3) can not be obtained precisely and finally induced the incoherence of STRETCH processing echo returns. Fig. 1 shows the phase difference curves of adjacent echo pulses in STRETCH processing by using DCT method in a phased array radar. As shown in Fig. 1, the phase difference curve has tough undulation and cannot reflect the motion state of the target. This is due to the coherence destroying in STRETCH processing.

3.2 Coherent property of direct IF sampling

As is known to all, most of modern radars use the phase and frequency information instead of amplitude only for their main function. The radar coherent property plays a more and more important role in the system performance. Coherent radar sets higher requirements on radar frequency source. The frequency and phase stability of frequency source is the precondition of coherence in coherent radar. Based on the coherence mentioned above, we can ensure the coherent property of echo pulses sampling directly in IF by proper design of system parameters.

Fig. 1 Phase difference curves of adjacent echo pulses achieving by STRETCH processing

As for the coherent pulse compression radar, in order to keep the coherent property of echo pulses sampled directly in IF, there are some constraints to the sampling frequency. We usually adopt pulse train sampling or pulse sampling in the present existing direct IF sampling systems. Compar- atively, pulse train sampling is more suitable for keeping coherence of echo pulses. In Ref. [13], two conditions for keeping coherence in pulsed radar are summarized:

(1) band-pass signal non-aliasing sampling rule

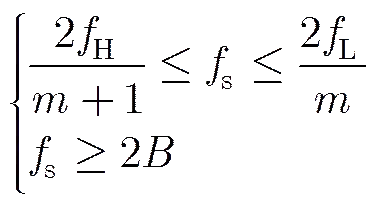
(2) coherent requirement of adjacent pulses

Then we’ll proof the coherent property of echo signals sampled directly in IF bellow. The LFM signal used by radar can be expressed as

(5)

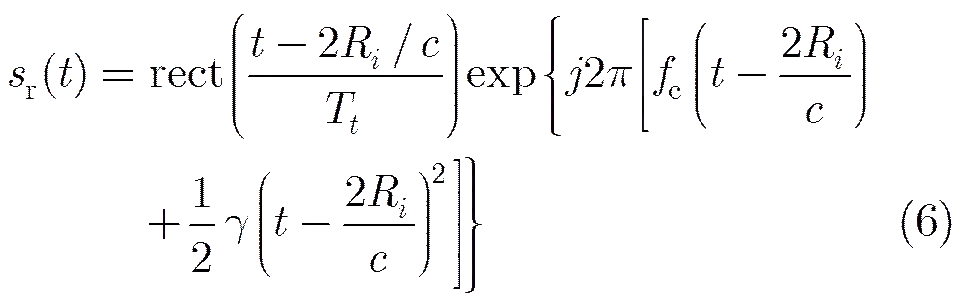
After mixing process, the echo returns are converted down to IF signal, which can be express as

(7)

According to the stationary phase principle, we obtain the frequency domain expression offrom Eq. (8).

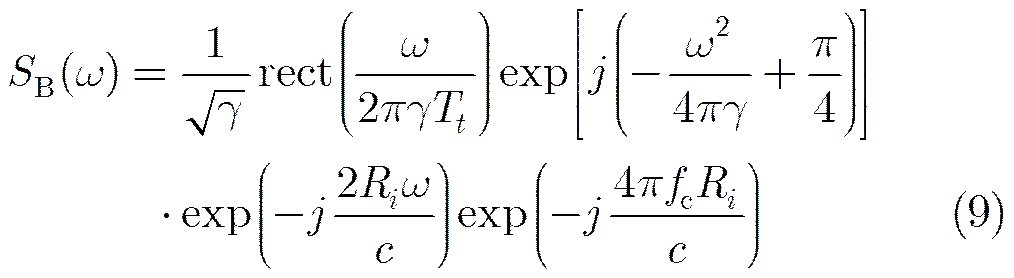
Then the matched filter of signal expressed by Eq. (9) can be written as

(10)

So the output signal of the matched filter can be expressed as

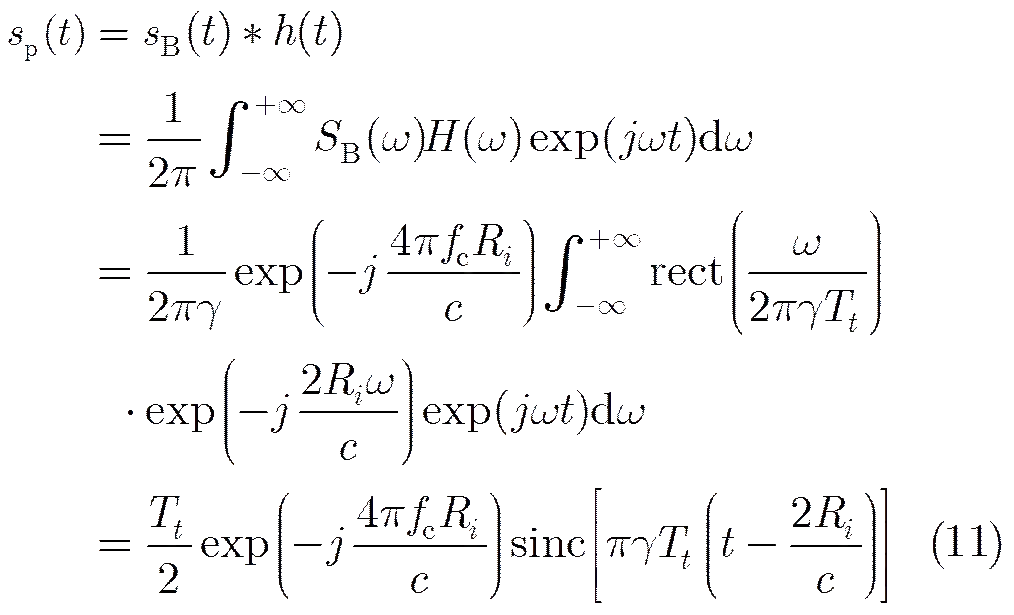
We can see from Eq. (9) that, the phase of signal after matched filtering is

(12)

Eq. (11) shows that, for the 1-D range profile of matched filtering after direct IF sampling, phase compensation means to eliminate the exponential term written aswhich truly reflects the phase variation induced by transla- tional motion of the target. The exponential term’s variation between pulses reflects the phase shift induced by target motion. Even though there may be accelerated motion during observation, the phase transformation curve induced by motion should be continuous and smooth because of the inertial. The non-ideal factors such as system distortion and radio propagation path just superimpose little ripple on the smooth curve.

Fig. 2 shows that the phase difference curve of adjacent echo returns sampled directly in IF is continuous and approximate smooth. The little ripple is induced by the non-ideal factors such as system distortion and radio propagation path. Also we can find from the figure that the phase difference has an increasing trend. This indicates the accelerated motion of the target.

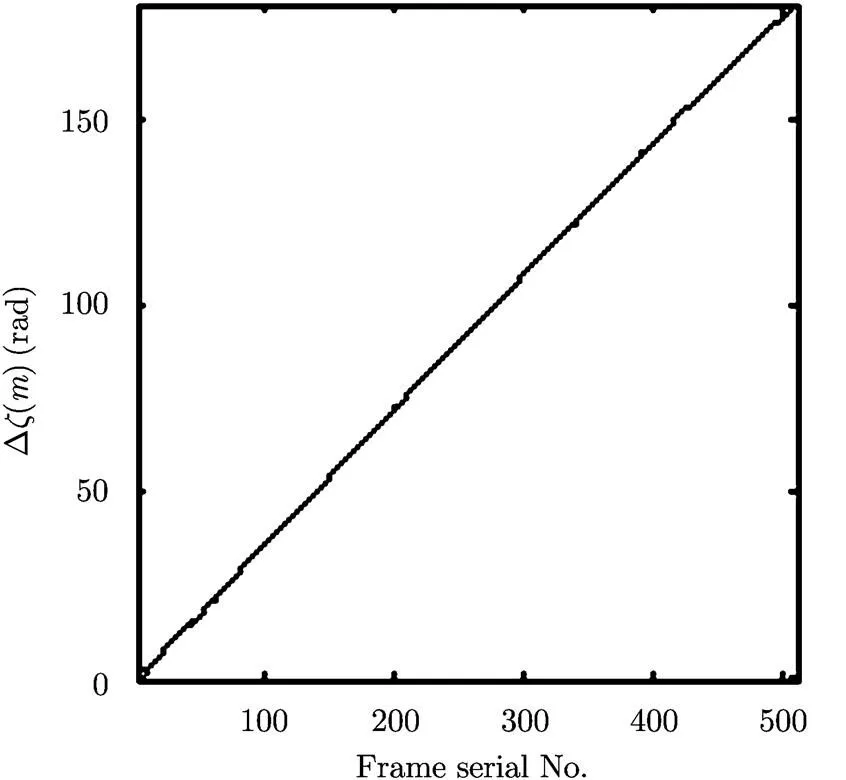
Fig. 2 Phase difference curves of adjacent echo pulses achieving by direct IF sampling

3.3 Coherent phase compensation method

Based on the coherent property of direct IF sampling, we can smooth the phase difference curve using the least squares curve fitting method, and eliminate the phase error. Then we achieve the accurate phase difference curve and can improve the phase compensation effect.

The concrete steps of the algorithm are shown bellow:

Step 1 Estimate the Doppler centroid phase difference complex exponential function shown in Eq. (1) using DCT method, so we can obtain the phase difference curve of adjacent echo returns (curve of);

Step 2 Do the curve fitting using the least squares curve fitting method, then we achieve the accurate phase difference function;

Step 3 Reconstruct the phase compensation exponential functionusing. Socan be express as

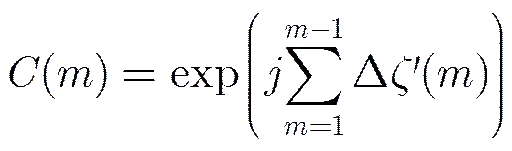
Step 4 Implement the phase compensation by multiplying the 1-D range profile data with the corresponding.

Seen form the steps above, the algorithm proposed in this paper is on the basis of DCT method, and improves the translational phase estimation accuracy using one-time curve fitting. It resolves the heavy computation load problem in Ref. [4] and is fit for engineering application.

4 Experimental Verification and Analysis

In order to verify the algorithm analyzed above, we compare it with unmodified DCT method and MDCT method in this section. Aircraft echo data sampled by an experimental phased array radar is adopted. Fig. 3 shows the difference between pre- and post curve fitting. This figure indicates that there are errors between the phase estimated by DCT method and that induced by target motion. The difference, which is just the negative influences of the RPC and other system factors on the TPC estimation accuracy, is lies within the scope of ±0.6 rad. ISAR imaging is processed after phase compensation using the phase difference function achieved by the least squares curve fitting method. It is important to choose a proper polynomial order when using curve fitting in Step 2 of the algorithm. Experimental shows that, in order to reflect the actual phase change induced by motion of the space or air targets as much as possible, the polynomial order should be set to 3.

Fig. 4(a) shows the ISAR image obtained using unmodified DCT method, while Fig. 4(b) are the ISAR image obtained by adopting the MDCT method and Fig. 4(c) via the novel phase compen- sation algorithm proposed in this paper. It is seen from the figure that, the imaging focus effect of Fig.4(c) is better than that of Fig. 4(a). So, the method proposed in this paper is effective and feasible.

The performance of phase compensation directly affects the quality of ISAR image which can be quantitatively evaluated by image entropy. Therefore, image entropy is adopted for the performance evaluation of phase compensation in this section. With the same other algorithms (such as distortion compensation, envelope alignment, image reconstruction,.), the better phase compensation performance, the higher image quality and lower image entropy. On the other hand, the worse phase compensation performance, the lower image quality and higher image entropy.

We accomplished the phase compensation for the aircraft echo returns mentioned above by using unmodified DCT method, MDCT algorithm and the strategy proposed in this paper respectively. Then the ISAR image entropies are obtained and shown in Tab. 1.

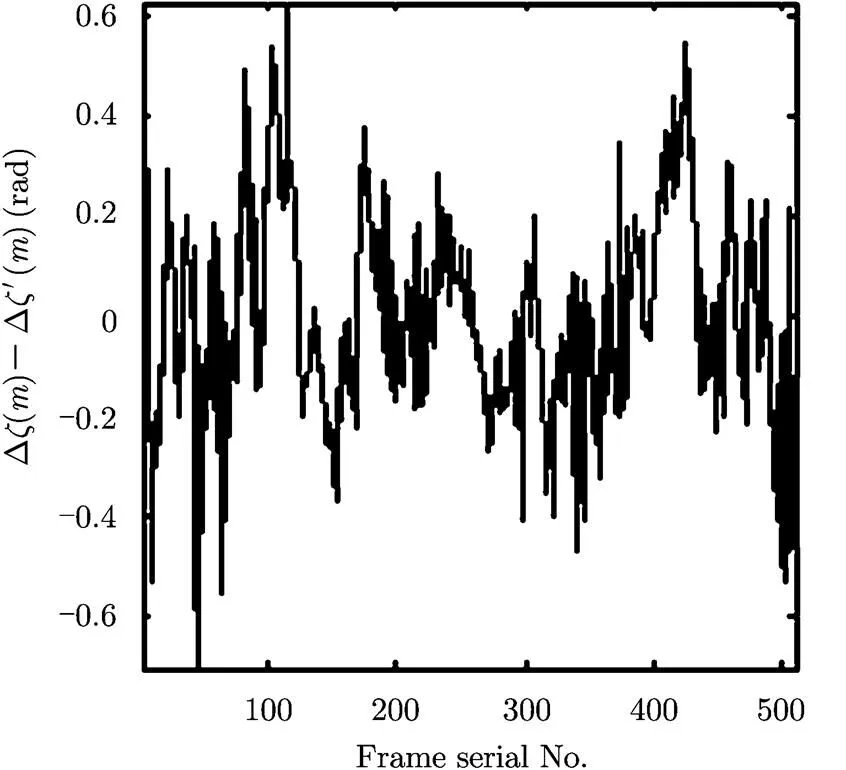
Fig. 3 Difference between pre- and post fitting

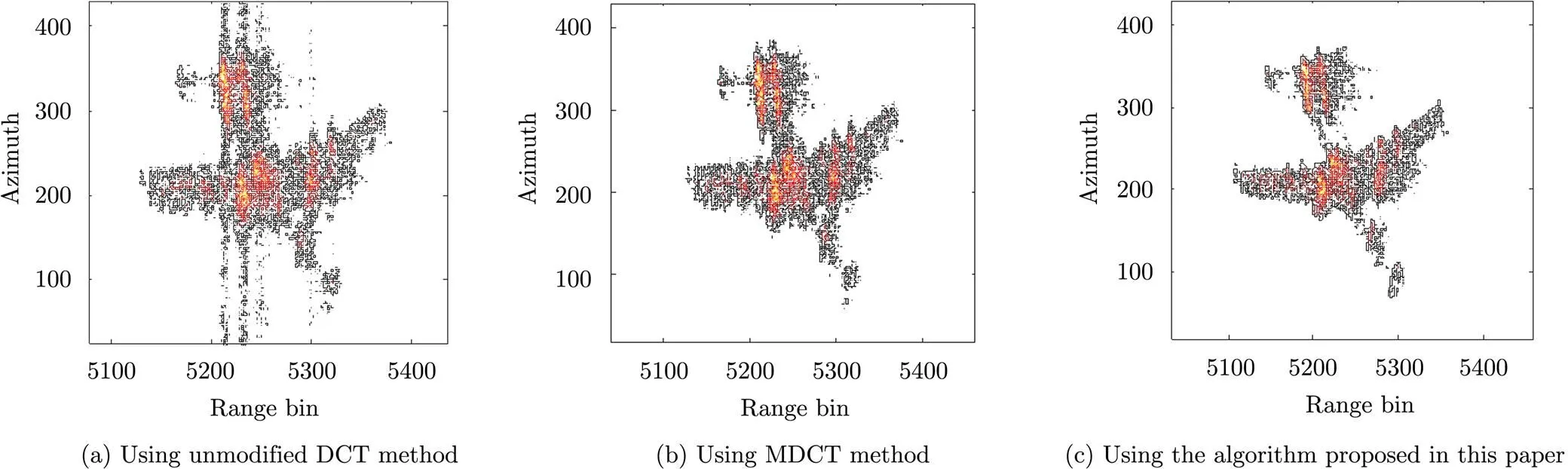
Fig. 4 ISAR imaging results of three methods

Tab. 1 Entropies of the three ISAR images obtained by using three phase compensation methods respectively

In a word, compared with the MDCT method, our method improves the unmodified DCT method and achieves better performance of phase compen- sation.

5 Conclusion

The coherence plays a more and more important role in radar system performance. Employing the coherent property of echo pulses, we can make better phase compensation in ISAR imaging. In this paper, the coherent property of echo pulses sampled directly in IF is obtained by analyzing, and a novel phase compensation algorithm is proposed to improve the translational phase estimation accuracy in DCT method, and then improve the quality of ISAR image. Experimental results prove the effectiveness and efficiency of the proposed strategy.

[1] Kaya A and Kartal M. Point scatterer model for RCS prediction using ISAR measurements[C]. Proceedings of 4th International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 2009: 422-425.

[2] Cao Min. Research on high resolution radar imaging technology for space targets[D]. [Ph.D. dissertation], National University of Defence Technology, 2008: 7-10.

曹敏. 空间目标高分辨雷达成像技术研究[D]. [博士论文], 国防科技大学, 2008: 7-10.

[3] Ye Chun-mao, Xu Jia, Peng Ying-ning,.. Performance analysis of Doppler centroid tracking for ISAR autofocusing[J]., 2009, 37(6): 1324-1328.

叶春茂, 许稼, 彭应宁, 等. 逆合成孔径雷达多普勒质心跟踪法性能分析[J]. 电子学报, 2009, 37(6): 1324-1328.

[4] Zhu Zhao-da, Qiu Xiao-hui, and She Zhi-shun. ISAR motion compensation using modified Doppler centroid tracking method[J]., 1997, 25(3): 65-69.

朱兆达, 邱晓晖, 佘志舜. 用改进的多普勒中心跟踪法进行ISAR运动补偿[J]. 电子学报, 1997, 25(3): 65-69.

[5] Ye Chun-mao, Ning Xia, Yang Jian,.. Parallel implementation of a block-wise phase gradient autofocusing method[J].(), 2012, 52(5): 612-615.

叶春茂, 宁夏, 杨健, 等. 一种分块相位梯度自聚焦算法的并行实现[J]. 清华大学学报(自然科学版), 2012, 52(5): 612-615.

[6] Krichene H A, Pekala M J, Sharp M D,.. Compressive sensing and stretch processing[C]. Proceedings of 2011 IEEE Radar Conference (RADAR), Kansas, 2011: 362-367.

[7] Lina Yeh, Kainam Thomas Wong, and Hasan Saeed Mir. Viable/inviable polynomial-phase modulations for “stretch processing”[J]., 2012, 48(1): 923-926.

[8] Lin Qian-qiang, Tang Peng-fei, and Chen Zeng-ping. Design and implementation of direct IF sampling and high-speed storage system for wideband radar[J]., 2012, 1(3): 283-291.

林钱强, 唐鹏飞, 陈曾平. 宽带雷达中频直接采样与高速存储系统设计与实现[J]. 雷达学报, 2012, 1(3): 283-291.

[9] Bao Zheng, Xing Meng-dao, and Wang Tong. Radar Imaging Technology[M]. Beijing: Publishing House of Electronics Industry, 2005: 24-26.

保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 24-26.

[10] Pricket M J and Chen C C. Principle of inverse synthetic aperture radar (ISAR) imaging[C]. IEEE EASCON Record, Virginia, 1980: 340-345.

[11] Yi Wen. Radar Receiver Technology[M]. Beijing: Publishing House of Electronics Industry, 2005: 131-136.

弋稳. 雷达接收机技术[M]. 北京: 电子工业出版社, 2005: 131-136.

[12] Cai Fei, Fan Hong-qi, Lin Hua,.. IF receiving method for pulsed coherent radar[J].&, 2011, 26(4): 457-462.

蔡飞, 范红旗, 林华, 等. 相参脉冲雷达中频直接接收方式研究[J]. 数据采集与处理, 2011, 26(4): 457-462.

[13] Ma Bo-tao, Fan Hong-qi, and Fu Qiang. IF sampling conditions for coherent pulse radar[J].&, 2009, 24(1): 114-118.

马博韬, 范红旗, 付强. 相参脉冲雷达中频采样条件研究[J]. 数据采集与处理, 2009, 24(1): 114-118.

[14] Pi Yi-Ming, Yang Jian-yu, Fu Yu-sheng,.. SAR Imaging Theory[M]. Chengdu: University of Electronic Science and Technology Press, 2007: 27-32.

皮亦鸣, 杨建宇, 付毓生, 等. 合成孔径雷达成像原理[M]. 成都: 电子科技大学出版社, 2007: 27-32.

[15] Li Xi, Liu Guo-sui, and Ni Jin-lin. Auto-focusing of ISAR images based on entropy minimization[J]., 1999, 35(4): 1240-1252.

[16] Jeong H R, Kim H T, and Kim K T. Application of subarray averaging and entropy minimization algorithm to stepped- frequency ISAR autofocus[J]., 2008, 56(4): 1144-1154.

[17] Cao Pan, Xing Meng-dao, Sun Guang-cai,.. Minimum entropy via subspace for ISAR autofocus[J]., 2010, 7(1): 205-209.

宽带雷达ISAR成像相位补偿新方法

陈曾平 张炜承 林钱强

(国防科技大学ATR国防科技重点实验室 长沙 410073)

为了消除目标强散射中心的转动相位分量对传统多普勒中心跟踪(DCT)相位补偿方法性能的影响，该文提出了一种新的相位补偿方法。该方法通过分析得出中频直接采样回波信号脉间相参的特点，并利用相参性改进DCT相位补偿方法对平动相位分量估计的精度，从而提高相位补偿效果，改善ISAR成像的质量。相对于MDCT法，该方法能够达到更好的相位补偿效果。实测数据验证了该方法是一种可行、高效的相位补偿方法。

宽带雷达；相位补偿；中频直接采样；曲线拟合

TN95

A

2095-283X(2013)01-0023-07

Lin Qian-qiang.E-mail: Even_qqlin@163.com.

CLC index: TN95

10.3724/SP.J.1300.2013.13023

Manuscript received March 13, 2013; revised March 18, 2013.

Published online March 27, 2013.

Supported by the National Government Foundation of China.

Chen Zeng-ping (1967-) was born in Fuqing, Fujian province. He received the Ph.D. degree from National University of Defense Technology (NUDT) in 1994. Currently, he is a professor of NUDT and the vice director of ATR National Defense Science and Technology Key Lab. His research interests are radar signal processing and automatic target recognition. E-mail: atrchen@sina.com

Zhang Wei-cheng (1982-) was born in Changsha, Hunan province. He is pursuing the Ph.D. degree in ATR Key Laboratory of National University of Defense Technology. His research interests are radar imaging and signal processing.E-mail: zhangweicheng_iet@163.com

Lin Qian-qiang (1983-) was born in Putian, Fujian province. He is pursuing the Ph.D. degree in ATR Key Laboratory of National University of Defense Technology. His research interests are radar data acquisition and signal processing.E-mail: Even_qqlin@163.com