基于导航信号的BiSAR成像技术

2013-07-25田卫明

雷达学报 2013年1期

田卫明* 曾涛胡程

基于导航信号的BiSAR成像技术

田卫明曾涛胡程

(北京理工大学信息与电子学院北京 100081)

该文研究了导航卫星照射的BiSAR系统的成像处理技术，针对导航信号BiSAR成像所存在的特殊问题，利用直达波信号提取距离徙动参数并在方位时域实现了距离徙动的校正，通过多普勒补偿的方法解决了导航信号对多普勒敏感的问题，利用对直达波信号的相位历程进行高阶多项式拟合实现了对多普勒相位历程的精确近似，方位向通过去斜处理实现方位向聚焦。仿真数据和实测数据的成像处理结果验证了该算法的正确性。

双基地合成孔径雷达；导航信号；直达波；成像

1 引言

基于星载照射源的双基地合成孔径雷达(Bistatic Synthetic Aperture Radar, BiSAR)能够在不增加卫星设备的条件下以无源方式进行遥感成像，利用导航卫星和通信卫星作为照射源还实现了利用非雷达卫星信号进行BiSAR成像，可以实现对观测区域的长时间观测，相关的研究工作具有重要的理论意义和应用前景。本文研究的导航卫星照射的BiSAR系统除具备BiSAR系统的特性外，导航卫星在轨道高度、信号形式上与雷达遥感卫星存在明显差异，主要表现在以下几个方面：(1)信号形式的改变；(2)2维频谱表达式无法获得；(3)长合成孔径时间，大距离徙动；(4)导航信号的脉冲压缩对多普勒敏感；(5)多普勒相位高阶误差显著。

针对导航信号进行BiSAR成像的特殊问题，本文研究了适用于导航信号的BiSAR系统成像方法：该方法通过距离和方位的级联处理实现2维成像处理，避免了在2维频域进行操作，同时考虑到导航信号的特殊性采用了多普勒相位补偿、高阶徙动校正和多普勒相位历程高阶近似的方法有效解决了导航信号进行BiSAR成像所带来的特殊问题，通过对仿真数据和实测数据的处理验证了该算法的可行性。

2 基于导航信号的BiSAR信号模型

利用导航卫星作为照射源，在飞机、山顶或飞艇平台上搭载接收机就可以组成BiSAR系统，根据接收机是否运动又可以分为星-机模式和星-地模式，系统示意图如图1所示。导航卫星照射的BiSAR系统属于非合作BiSAR系统，为了实现卫星与接收机间的时频同步，接收机一般具备直达波信号接收通道用于接收直达波信号实现时频同步，如图1中的虚线所示。

2.1信号模型

卫星导航系统采用原子钟提供频率基准，具有极高的频率准确度，可以认为导航卫星的发射信号为准严格意义上的周期信号，导航信号的基带调制信号为周期性的伪随机序列，信号中同时调制了导航电文数据，典型导航卫星的发射信号表达式如式(1)所示：

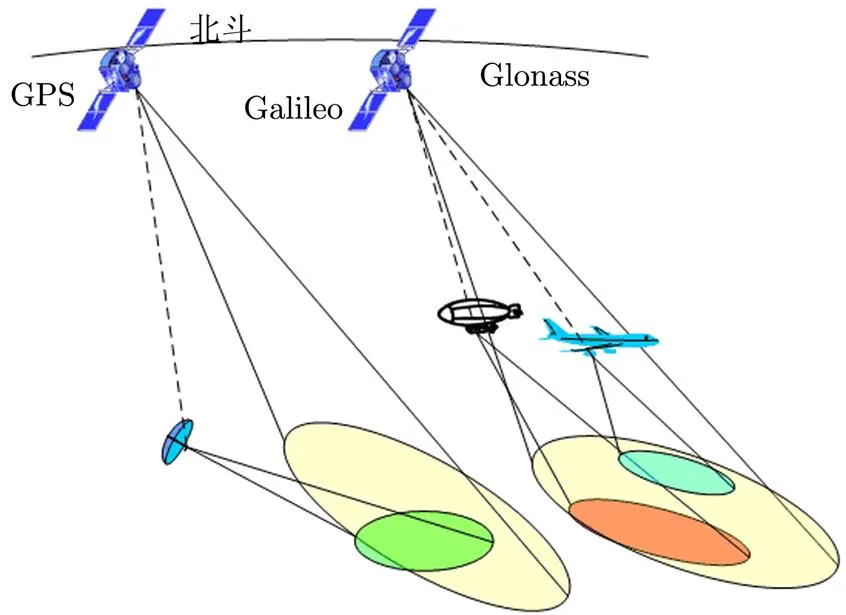
图1 基于导航卫星照射的BiSAR系统

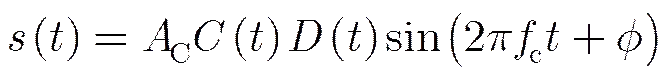
(2)

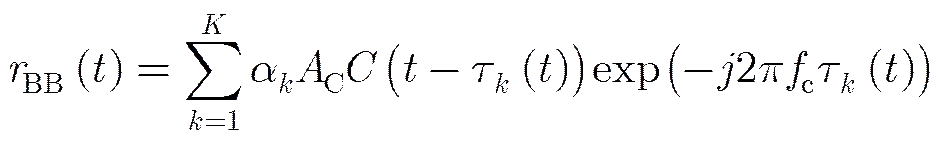
2.2 2维分块

导航信号为连续波信号，而SAR成像处理一般为2维信号，因此首先需要将1维原始信号划分为2维时域信号，理论上连续波信号可以以任意时间间隔作为等效脉冲重复间隔来划分快慢时间，但实际操作时还需要考虑分块长度对距离向脉冲压缩的峰值旁瓣比、距离模糊、多普勒混叠和成像处理效果等各方面的影响。连续波信号的占空比为1，划分脉冲重复间隔后等效脉冲重复频率和等效脉冲宽度将互为倒数关系，即

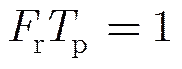
此外等效脉冲重复间隔还将影响距离向脉冲压缩输出，图2(a)和图2(b)显示了GPS信号在不同相关时间时所对应的相关输出特性，图2(a)中相关时间为1 ms，峰值旁瓣比为24 dB，图2(b)中相关时间为0.1 ms，峰值旁瓣比为14 dB，通过比较可以发现相关时间每降低一个数量级，峰值旁瓣比将恶化10 dB，而SAR成像处理要求峰值旁瓣比优于20 dB，根据GPS信号中C/A码的周期自相关特性可知等效脉冲宽度必须在0.7 ms以上，GPS信号中C/A码的重复周期为1 ms，因此将1 ms作为等效脉冲重复间隔进行2维分块处理是合理的划分方式，此时等效于脉冲重复频率为1000 Hz，能够保证多普勒信号频谱不产生混叠。

经过快慢时间划分后1维离散信号可以变为2维矩阵，2维分块后回波信号表达式变为

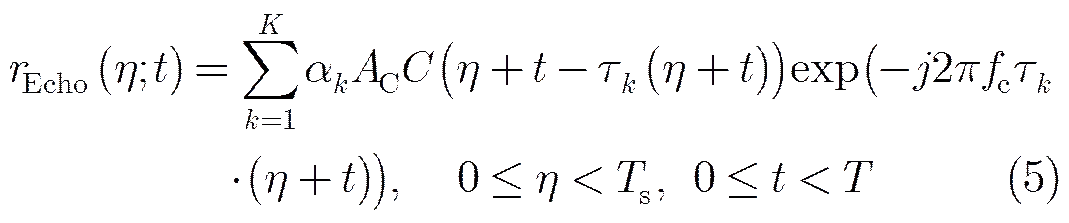
图2GPS信号C/A码相关时间对副瓣的影响

Fig. 2 Impacts of correlation time for side-lobes of GPS signal C/A code

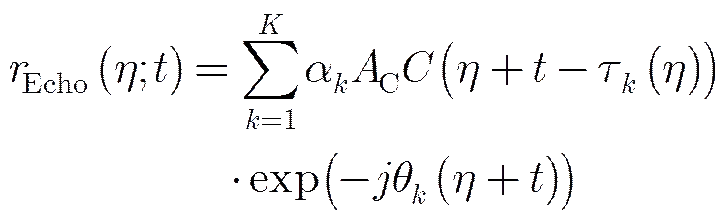
3 导航卫星照射的BiSAR成像算法

针对利用导航信号进行BiSAR成像存在的特殊问题，本节提出了一种导航信号的BiSAR成像处理方法，该方法中通过多普勒中心频率相位补偿解决了导航信号对多普勒敏感的问题，利用直达波信号提取距离徙动信息和多普勒相位历程，通过双基地的几何关系实现回波信号距离徙动和多普勒相位历程，通过对多普勒相位进行高阶近似解决了长合成孔径时间的聚焦问题，通过对仿真数据和实测实验数据的处理，验证了该算法的正确性。

3.1 距离徙动和多普勒参数估计

在基于星载照射源的BiSAR系统中，直达波信号非常适用于估计BiSAR的成像参数，接收系统采用直达波和回波信号同时接收的双通道接收系统，两个接收通道共用同1个本振信号保证了两个通道间信号相位的相参性和时频同步误差的一致性，从而为直达波信号辅助回波信号成像奠定了基础。

补偿了直达波信号的时间和频率误差后，可以从直达波信号中提取多普勒参数和距离徙动参数，在导航卫星照射的BiSAR系统中，根据双基地的几何关系可以得到直达波多普勒参数和距离徙动参数与回波信号的相互关系，获得回波信号的多普勒参数和距离徙动参数，用于回波信号的聚焦成像处理。

3.2多普勒相位补偿

回波信号的多普勒中心频率决定了方位向匹配滤波器的中心位置，对方位向分辨率的改善没有贡献，由于相位编码信号存在对多普勒敏感的问题，当2维分块后的多普勒相位在一条距离线中存在显著变化时就必须加以补偿，式(6)中的多普勒相位仍然可以用多项式来近似，如式(7)所示：

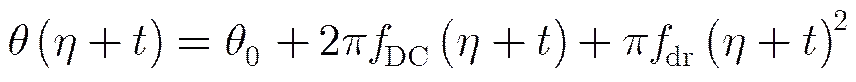
从匹配滤波角度出发，当一条距离线内最大相位变化量小于/4时对脉冲压缩的影响可以忽略，即式(8)和式(9)需要满足式(10)和式(11)的条件：

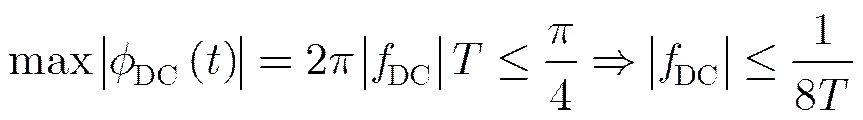
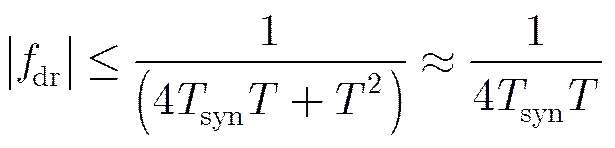
导航卫星照射的BiSAR系统的合成孔径时间在百秒量级，静止接收时回波信号的多普勒调频率绝对值在0.7 Hz/s以下，在基于GPS卫星照射的BiSAR实验中合成孔径时间为300 s，等效脉宽为1 ms，代入式(12)可得对应的多普勒调频率应当小于0.83 Hz/s，因此只需补偿多普勒中心频率引入的线性相位项即可，补偿相位表达式为

(13)

式(7)经过相位补偿后的剩余相位变为式(14)

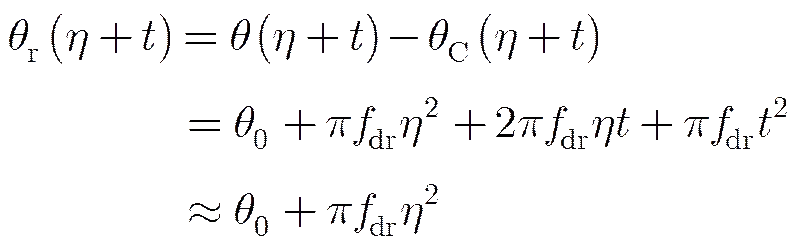
回波信号中不同目标的多普勒中心频率存在微小差异，补偿后存在一定的剩余线性相位，设回波信号中第个目标对应的多普勒中心频率为，用于补偿多普勒中心频率为，补偿后的剩余相位表达式为

(15)

为保证式(15)中的剩余线性相位不影响距离压缩，等效脉宽内需要满足式(16)：

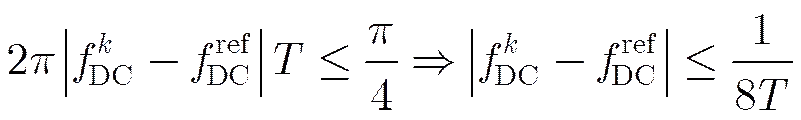
当=1 ms时不同目标的多普勒中心频率差小于125 Hz即可，该条件在一般的场景条件下能够满足，相位补偿后回波信号的表达式分别为

回波信号经多普勒中心频率补偿后可近似认为多普勒相位在一条距离线中的相位不再变化。

3.3距离压缩与徙动校正

导航信号的距离压缩仍然通过匹配滤波来实现，与线性调频信号脉冲压缩所使用的确定距离参考函数不同，式(17)中2维分块处理后每条距离线对应的伪随机码起始码相位不同，因此距离参考函数必须随慢时间更新，根据相位补偿后回波信号的表达式(17)可知每条距离线的表达式为

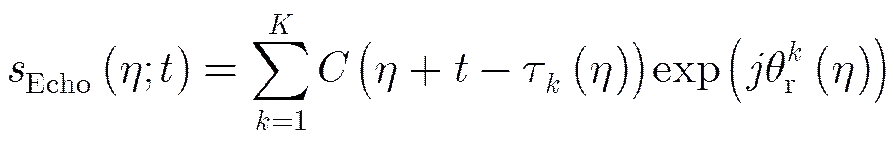
(19)

导航卫星照射的BiSAR系统，长合成孔径时间条件下距离徙动的高阶分量显著，因此距离徙动校正必须对距离弯曲和距离走动同时予以校正。利用直达波信号斜距历史得到回波信号的距离徙动参数后，就可以利用该参数对回波信号进行距离徙动校正，在距离参考函数中增加用于距离徙动校正的线性相位因子，距离压缩和距离徙动校正后的信号表达式变为式(20)：

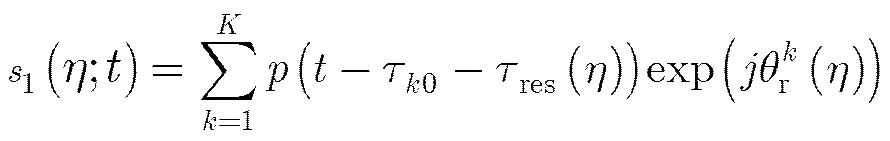
3.4 方位向处理

在导航卫星照射的BiSAR系统中，当接收机静止接收时只有卫星与场景间的相对运动会产生斜距历程，接收机至场景只在双基地距离和中引入固定距离，斜距历程的表达式为式(21)：

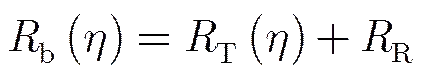
(22)

GPS卫星照射的BiSAR系统在长合成孔径时间和大前斜条件下工作，多普勒相位历程中的高阶相位表现明显，因此对多普勒相位历程必须进行更高阶的近似，图3是仿真得到的不同阶次的近似误差，从中可见4阶相位近似能够满足成像处理要求。

当多普勒相位历程在4阶相位的近似条件下将回波信号的多普勒相位历程使用式(23)来表示：

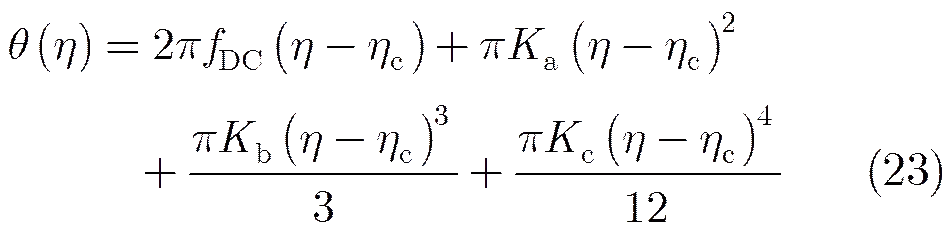
式(23)中为多普勒中心频率，, 和分别对应了多普勒线性调频率，2次调频率和3次调频率，为目标对应的孔径中心时刻，在静止接收机接收和小场景条件下，场景内各散射点的多普勒相位历程近似满足平移不变性，因此式(23)仍假定不同目标的多普勒相位历程具有平移不变性。当方位向聚焦采用deramping方式实现时，一般选择场景中心处目标回波信号的相位历程作为去斜参考相位，在多普勒相位满足平移不变性的条件下去斜参考相位表达式可以表示为

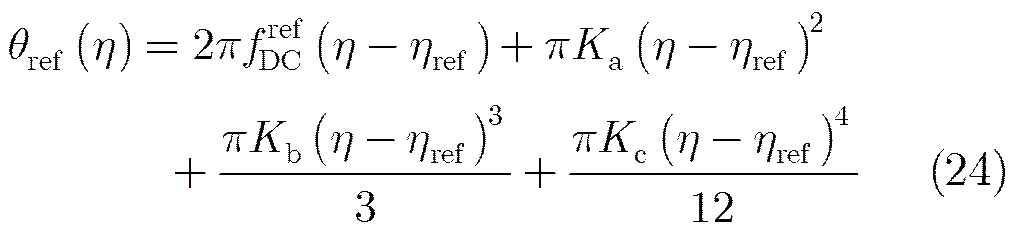
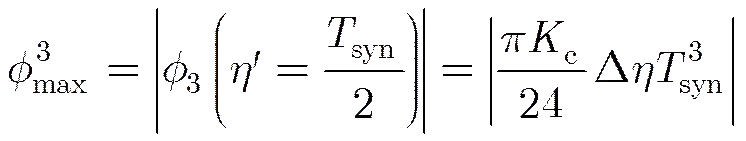
式(26)中的3次相位误差仅由多普勒相位历程中的4次相位经去斜处理后引入，式(27)的2次相位误差则由多普勒相位历史中的4次相位和3次相位共同产生，从成像处理角度看，/4的2次相位误差和/8的3次相位误差是可以接受的误差上限，即最大的3次相位误差和2次相位误差满足：

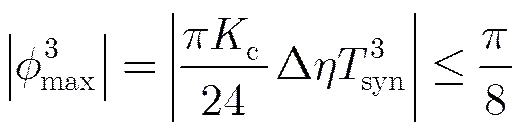
(29)

根据式(28)和式(29)，当已知回波信号的子孔径处理时间、多普勒2次调频率和3次调频率时就可以确定最大的，式(29)中，因此式(29)的限制条件可以近似为

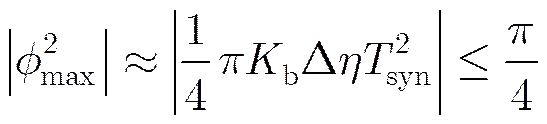
(31)

使用GPS卫星作为照射源进行BiSAR成像时波束在地面移动速度约为1 km/s，合成孔径时间为300 s，将多普勒2次调频率和3次调频率代入到式(31)中可以得到1次成像能够处理的最长时间间隔，从实测数据的处理结果可知多普勒2次调频在Hz/s量级，多普勒3次调频在Hz/s量级，图4为多普勒2次调频和3次调频对要求，从中可见多普勒3次调频对的约束较强，当多普勒3次调频率为Hz/s时有效成像时间间隔约为2 s，对应方位向的场景宽度为2 km左右，能够满足实验条件下的成像处理要求，而对于更大范围的成像处理则需要进行分块处理。

4 仿真数据和实测数据的成像处理结果

为了验证算法的可行性，这里分别对模拟回波数据和GPS卫星照射的BiSAR实验中获得的实测数据进行了成像处理。模拟回波数据采用了真实的GPS卫星轨道参数来产生回波信号和直达波信号，直达波和回波接收机的配置情况与实验情况一致，对实验中获取的GPS卫星照射的BiSAR实验对直达波信号和回波信号进行了成像处理。直达波信号的信噪比高，信号形式简单，可以看做孤立点目标的回波信号，直达波信号的成像处理结果即为GPS信号的点扩展函数，图5(a)和图5(b)分别显示了直达波信号方位向和距离向的压缩结果，由于多普勒相位历程中多普勒线性调频对应的2次相位是主要部分，因此方位向压缩结果近似为sinc函数的形状，距离向副瓣结构由伪随机码的自相关函数决定，与sinc函数具有明显的差异。

实验过程中在场景中放置了角反射器形成强散射点用于对分辨率进行评估，某次实验的成像结果和场景光学照片如图6所示，图7是对方位向分辨率的分析结果，其中两个角反射器峰值距离14 m，方位向3 dB主瓣宽度为4.8 m，方位向分辨率与理论分析结果一致。

图4 多普勒2次调频和3次调频对的要求

Fig. 4 Requirement offor Doppler quadratic and cubic FM rate

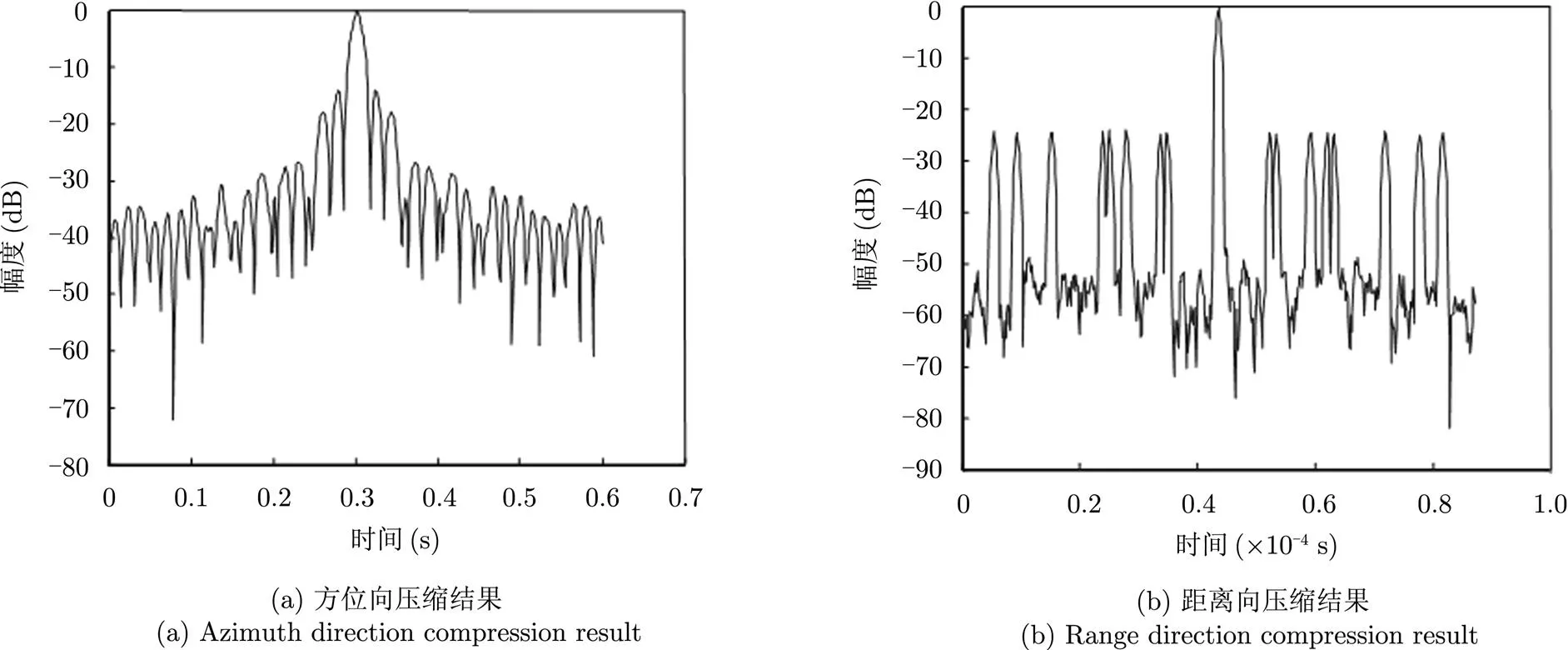
图5 GPS直达波信号方位向和距离向的压缩结果

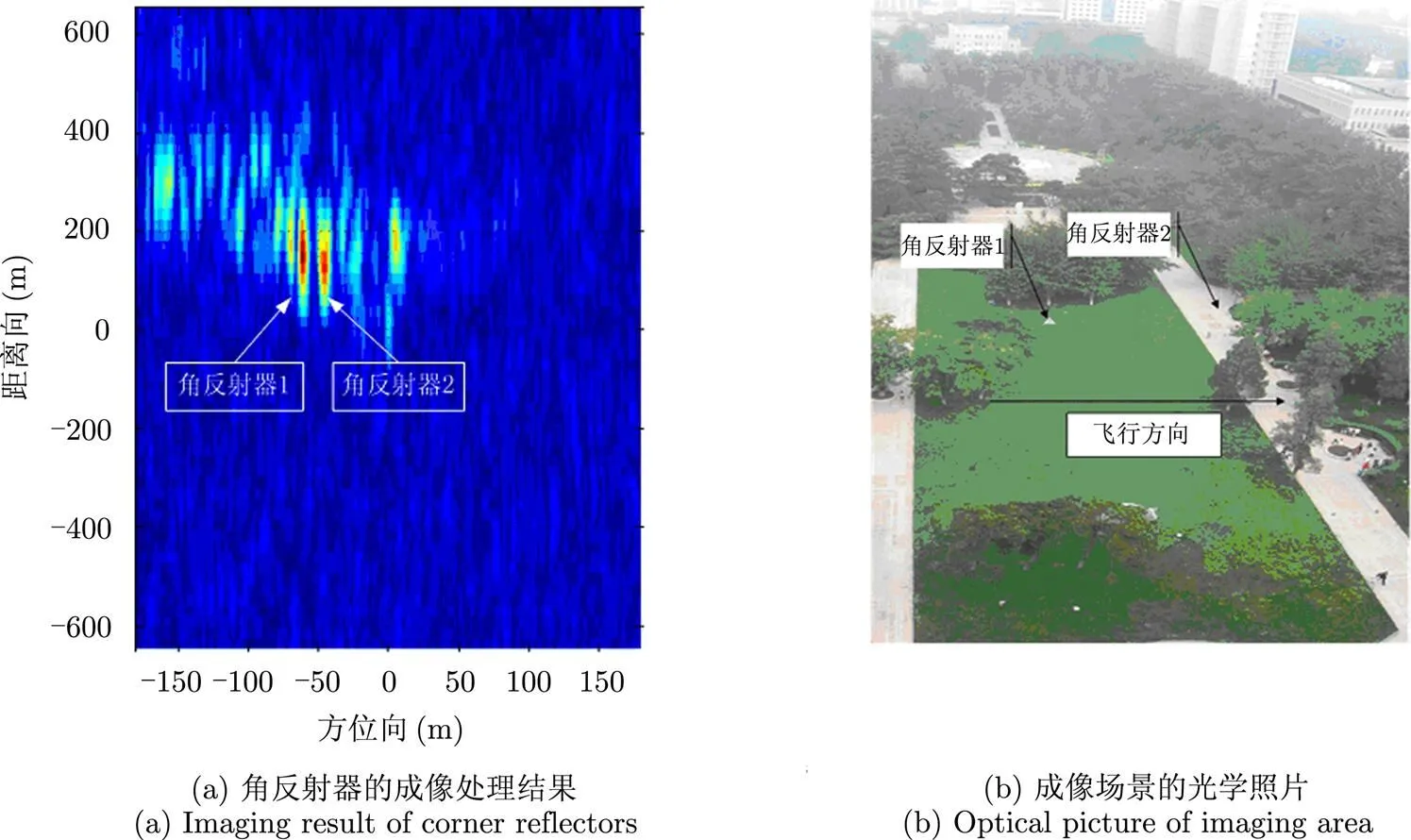
图6 实测数据的成像处理结果与场景光学照片

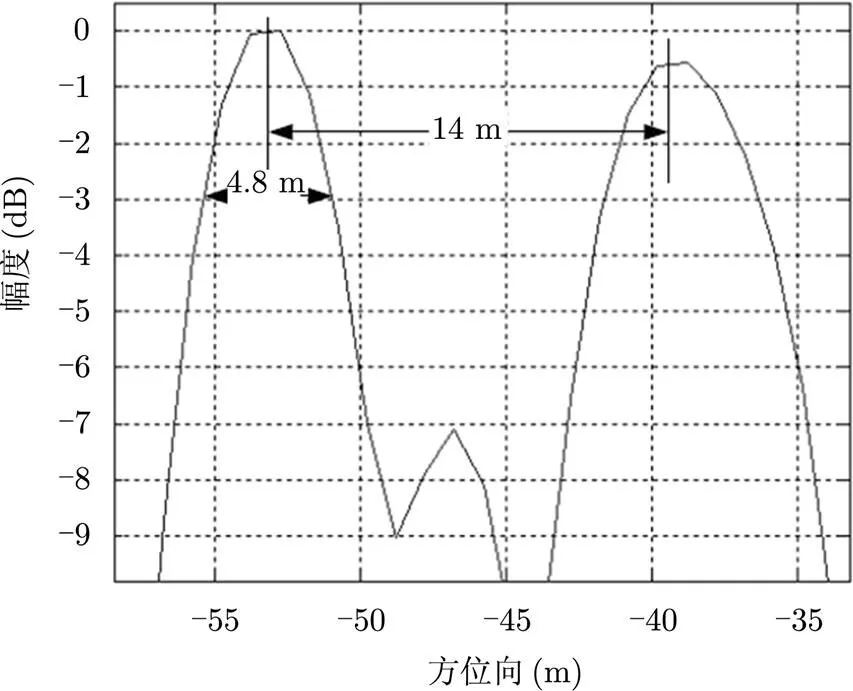
图7 实测数据的方位向分辨率分析

5 小结

本文研究了导航卫星照射的BiSAR系统的成像算法，提出了适用于导航信号BiSAR成像的成像算法，该算法中通过补偿多普勒相位解决了导航信号对多普勒敏感的问题，在距离徙动校正时考虑了斜距模型中的高阶项，并对高阶徙动分量进行校正解决了原有算法中距离走动校正精度不足的问题，在方位向deramping处理时通过对多普勒相位历程进行高阶近似解决了菲涅尔近似误差较大的问题，通过对仿真数据和实测数据的处理结果验证了该算法的可行性。

[1] Homer J, Kubik K, Mojarrabi B,.. Passive bistatic radar sensing with LEOS based transmitters[C]. Toronto: IGARSS, 2002, 1: 438-440.

[2] Walterscheid I, Espeter T, Gierull C,.. Results and analysis of hybrid bistatic SAR experiments with spaceborne, airborne and stationary sensors[C]. 2009 IEEE International Geoscience and Remote Sensing Symposium, IGARSS, Cape Town, 2009, 2: 238-241.

[3] Keydel W. Perspectives and visions for future SAR systems [J].-,, 2003, 150(3): 97-103.

[4] Cherniakov M, Saini R, Zuo R,.. Space surface Bistatic SAR with space-borne non-cooperative transmitters[C]. European Radar Conference, France, 2005: 9-12.

[5] Antoniou M, Saini R, and Cherniakov M. Results of a space-surface bistatic SAR image formation algorithm[J]., 2007, 45(11): 3359-3371.

[6] Tian Weiming, Hu Shanqing, and Zeng Tao. A frequency synchronization scheme based on PLL for BiSAR and experiment result[C]. International Conference on Signal Processing Proceedings, 2008: 2425-2428.

[7] Elliott D Kaplan and Christopher J Hegarty. Understanding GPS Principles and Applications[M]. 2nd Edition, New York: ARTECH HOUSE, INC., 2006.

[8] Ender J, Brenner A, and Loffeld O. Bi-static SAR processing and experiments[J]., 2006, 44(10): 2710-2717.

[9] Lopez-Dekker P, Mallorqui J J, Serra-Morales P,.. Phase and temporal synchronization in bistatic SAR systems using sources of opportunity[C]. 2007 IEEE International Geoscience and Remote Sensing Symposium, IGARSS, Barcelona, 2007, 1: 97-100.

[10] ICD-GPS-200C. 13th, Oct, 1993. http://www.navcen.uscg.gov/ pubs/gps/icd200/icd200cw1234.pdf.

[11] 林茂庸, 柯有安. 雷达信号理论[M]. 北京: 国防工业出版社, 1984: 153.

Lin Mao-yong and Ke You-an. Radar Signal Theory[M]. Beijing: National Defence Industry Press, 1984: 153.

[12] 张澄波. 综合孔径雷达: 原理, 系统分析与应用[M]. 北京: 科学出版社, 1989: 163-178.

Zhang Cheng-bo. Synthetic Aperture Radar: Principle, System Analysis and Application[M]. Beijing: Science Press, 1989: 163-178.

Imaging Algorithm for Bistatic SAR Based on GNSS Signal

Tian Wei-ming Zeng Tao Hu Cheng

(School of Information and Electronics, Beijing Institute of Technology, Beijing 100081, China)

In this paper, an imaging processing method for Bistatic Synthetic Aperture Radar (BiSAR) utilizing navigation satellites is investigated. Considering the special problems regarding the use of Global Navigation Satellite System (GNSS) signals to form SAR images, direct signals are used to estimate range migration parameters, and range migration is corrected in the azimuth time domain. The Doppler sensitivity of phase-coded signals was solved by Doppler compensation. By fitting the Doppler phase history with a high-order polynomial, the Doppler phase history is accurately approximated and the azimuth compression is implemented by de-chirp processing. By performing simulations and experimental data processing, the proposed method is verified.

Bistatic Synthetic Aperture Radar (BiSAR); Global Navigation Satellite System (GNSS) signal; Direct signal; Imaging

TN95

2095-283X(2013)01-0039-07

10.3724/SP.J.1300.2013.20092

田卫明(1983-)，男，河南焦作人，2010年获北京理工大学工学博士学位，北京理工大学讲师，主要研究方向为双基地SAR系统与信号处理、高分辨SAR系统。E-mail: tianwei6779@163.com