微多普勒理论在海面目标检测中的应用及展望

陈小龙 关 键* 何 友



微多普勒理论在海面目标检测中的应用及展望

陈小龙 关 键何 友

(海军航空工程学院电子信息工程系 烟台 264001)

微动特性是目标物理特性之一，微动目标的雷达特征包含了对目标形状、结构和运动的精细刻画，同时微多普勒反映了信号的非平稳特性，因此，在高海况条件下采用微多普勒理论分析海杂波及检测海面目标具有很大的优越性。该文首先从微多普勒机理和特点出发，对动态海面散射杂波建模和海杂波多普勒特性分析方法等相关研究进行归纳与分析，表明微多普勒理论应用的必要性；然后，从海面微动目标回波建模和微动特征分析与检测方法等方面重点介绍了微多普勒理论在海面目标检测领域的应用和主要技术途径；最后，针对现有研究中存在的问题，阐述了有待于进一步研究的方向。

微动；微多普勒；海杂波；目标检测

1 引言

海杂波中微弱目标尤其是“低(低掠射角)、慢(静止或慢速运动)、小(目标尺寸小)”目标的检测技术始终是雷达信号处理领域的难题，不仅具有重要的理论意义，而且在军用和民用领域均占有非常重要的地位，如海面目标的检测、船舶的安全航行、浮冰规避和海洋环境的监测等。传统的基于统计理论的目标检测方法将海杂波视为随机过程，但目标模型和杂波模型均呈多样化发展趋势，尤其是杂波分布模型，在复杂环境中往往不成立或不完全成立，这就使经典目标检测方法由于模型失配而不能取得预期的检测结果。Haykin等人从混沌和分形角度出发，采用关联维数和盒维数等特征量从海杂波中检测微弱目标，但当信杂比持续降低时，检测结果却不尽人意，而且也很难实现对运动目标的检测。

研究表明，强海杂波背景下，杂波幅度概率密度函数表现出较长的“拖尾”现象，并且此时的多普勒谱展宽，体现出明显的时变和非平稳特性，它的统计特性和多普勒频率随时间变化，因此海杂波的频谱是时间和频率两个变量的函数，应从时间和频率两方面对海杂波数据进行分析和处理。同时，海上目标随海面颠簸导致姿态变化，引起雷达回波功率调制效应，不仅存在平动，舰船还绕参考点作三轴转动，导致散射点的多普勒频率随时间非线性变化。因此，新的检测算法应能较好地处理时变、非平稳和非线性信号，同时反映信号的精细特征。

在这种情况下，人们开始从其它方向寻找解决该问题的有效途径。近年来，微多普勒理论的研究已成为信号处理领域的一个新的技术热点。微多普勒反映了多普勒的变化特性，目标的几何结构和精细运动对雷达回波的综合调制特征则体现在目标的微动特征上，从而为雷达目标检测和特征提取提供了新的途径。目标距离的周期性将引起目标多普勒频率的周期性，多普勒谱出现展宽，目标姿态变化将对回波产生调制特性，反映出目标的瞬时速度变化特性，而海面目标，如舰船目标，其回波多普勒谱实质是平动和微动共同作用的结果。因此，微多普勒非常适于分析海杂波的非平稳特性以及海面目标回波信号。目前，虽然微多普勒的理论研究及应用处在起步阶段，仍有很多问题亟待解决，但已成为国内外的一大热点研究内容。本文从微多普勒效应的概念出发，首先介绍了海杂波多普勒建模及特性分析方法的国内外研究现状，在此基础上结合海面目标电磁散射特性和运动模型，对目标微动特征提取与检测方法进行总结和阐述，尤其对目前研究过程中出现的新方法进行了详细介绍，最后，针对现有研究中存在的问题，展望了微多普勒理论在对海雷达回波信号分析中的发展趋势，指出了进一步的研究方向。

2 微多普勒研究概述

微动最早出现在相干激光雷达中，美国海军研究实验室(Naval Research Laboratory)的Victor C. Chen最早提出了微动(Micro-motion)和微多普勒(Micro-Doppler)的概念并将其引入到雷达观测中，将目标或目标部件除质心平动以外的振动、转动和加速运动等微小运动统称为微动，而由目标微动所引起的多普勒频移称为微多普勒。国防科技大学的陈行勇等人又在此定义的基础上，将微动推广为“目标或目标组成部分在径向相对雷达的小幅非匀速运动或运动分量(相对于目标与雷达的径向距离)”。从多普勒效应来看，若点目标在雷达径向存在非匀速运动，则其多普勒随时间变化，表现为频谱展宽；同时，目标往往存在复杂的非刚体运动形式，各质元的相对运动也会使其回波频谱出现旁瓣或展宽，称为微多普勒效应(Micro-Doppler effect)。微多普勒反映了频率的瞬时特性，描述了微动引起的瞬时多普勒变化特性，因此微多普勒具有时变性，即频率随时间变化。自然界中普遍存在着微动现象， 如行人手臂和四肢的摆动，人体的心跳和呼吸时胸腔的运动，电动机，履带车、装甲车和汽车车轮，直升机旋翼，弹道导弹弹头的颤动(进动和章动)，船舶的颠簸和摆动以及天线的转动等。微动目标的雷达回波特征反映了目标的精细特征，如结构特性、电磁散射特性和运动特征等，因此，对于空间、空中、地面目标、海面舰船的探测和识别具有重要的意义。

目前，国外以美国海军研究实验室、加拿大防御技术研究中心、美国Texas大学、新加坡南洋理工大学为主的研究机构和院校对雷达目标微多普勒开展了较为系统的研究，逐渐形成了从目标调制模型、特征分析与提取到方法验证、实验测量的研究体系。在工程应用上，微多普勒测量雷达系统由单一的多普勒测量功能发展到同时具有高多普勒分辨率和高距离分辨率的测量能力，美国在此方面的研究水平一直处于国际领先地位。2000年，Philip Gatt等人成功研制双脉冲连续波激光雷达，成功探测地面和空中目标的微多普勒信号，将其用于特征提取和目标识别以及战场态势评估。2001年，美国Georgia技术研究院采用连续波雷达观测车辆目标的微动特征并进行特征提取，已应用于汽车安全预警系统的研发中；2002年，美国研制的THAAD GBR X波段雷达能够精确测量弹道导弹弹头的微动特征，并对真假弹头进行识别；2007年，美国Texas大学研制了X波段3个发射频率的多频连续波体制的微动测量雷达系统，能够在测量微多普勒的同时测距，采集并分析了行人、车辆和动物在不同机动情况下，多角度的微多普勒特征，其结果可用于目标自动检测和识别。鉴于有限的微波波段资源和昂贵的实验设备，2011年，英国伦敦大学的Alessio Balleri等人采用频率捷变超声雷达采集微多普勒特征，降低了试验成本，但受声信号在大气中极易衰减的限制，仅能用于近程探测，如室内和机场旅客的监视等。

在国内，国防科技大学、空军工程大学、中国航天二院二十三所和西安电子科技大学等多家科研机构均在微多普勒方面开展了一定的研究，在此方面有了一定的研究基础，但有关微多普勒理论和技术的研究尚未成熟，研究内容主要集中在微多普勒效应的应用研究，包括微多普勒特征建模、微动特征提取、微动目标雷达SAR和ISAR成像等方面；研究对象包括高速运动目标，如地面车辆如坦克、装甲车、导弹发射架等振动目标、海面角反射器、直升飞机为代表的旋翼目标、弹道导弹为代表的进动和章动目标以及行人等非刚体微动目标等。由此可见微多普勒已成为国内外的一大热点研究内容。

3 海杂波多普勒研究现状

由于海杂波对来自海面或接近海面的目标(包括低空掠海飞行的飞机、小型军舰、航海浮标以及漂浮在海上的冰块)的雷达回波的可检测性形成严重制约，因此对海杂波的研究不仅具有理论上的重要性，而且具有实践上的重要性。海杂波谱是海表面单个距离门内连续相干时间序列信号自相关函数的傅里叶变换，通常称为功率谱。由于海表面是运动的，海杂波谱将产生多普勒频移，所以也称为多普勒谱。海杂波谱是雷达相参处理、多普勒域杂波抑制和动目标检测的基础。下面分别从动态海面散射杂波建模、多普勒谱特性以及在海杂波中微弱目标检测中的应用等方面作回顾和总结。

3.1 动态海面散射杂波建模

由于海杂波谱与海表面的运动和海面的扰动状态密切相关，海面复杂的运动引起散射的电磁波产生多普勒频移、展宽、强度变化等特性，因此海杂波多普勒谱研究与海面的散射机理密不可分。近年来，人们对动态粗糙海面散射模型以及多普勒理论进行了广泛而深入的研究，在诸如雷达目标成像、海洋环境监测、电波传播、遥感、海面目标检测与跟踪等领域中都有极其重要的意义。目前随机粗糙面散射理论大致上可分为两大类：第1类是数值方法，该方法虽然计算精度高，但计算复杂、耗时；第2类是近似的可数值求解的方法，较为经典的有适用于大尺度随机起伏的Kirchhoff近似法、小尺度起伏的微扰法以及独立叠加这两种起伏的双尺度方法。第2类方法可以定量地解释粗糙面产生散射的物理现象，但是其适用范围、理论基础以及实际应用中的一些问题，如低掠入射情况和高海情等情况，仍然有待于进一步研究。另外，文献[24]将分形几何用于自然粗糙面的模拟，利用随时间变化的带限分形模型来模拟海面，研究了具有自仿射分形特征的1维、2维随机粗糙面的散射，但分形模型未考虑实际粗糙面的谱分布，需要选择合适的尺度描述海面起伏的剧烈程度，也不能反映海杂波多普勒的变化情况。

海浪由大尺度重力波和小尺度张力波组成，可将海面简化为仅含有两种尺度粗糙度的表面，即大尺度粗糙面和小尺度粗糙面，根据这一特性，提出了粗糙面电磁散射的双尺度模型。然而，双尺度法依赖粗糙面的划分方式，且该模型基于海面散射回波信号是非时变的，即频率不随时间发生变化。 近年来，更多的研究表明，在高分辨率雷达对海观测中，当以低掠射角照射粗糙海面或高海况时，海面回波强度会明显增强，相应的杂波幅度概率密度函数表现出较长的“拖尾”现象，海面出现白浪等破碎波，雷达回波表现为海尖峰；文献[26]指出此时的多普勒谱包括由“慢变信号”引起的Bragg散射，以及“快变信号”产生的非Bragg散射，非Bragg散射导致Bragg谱展宽，海面散射回波信号由非时变向时变转变。海尖峰是海杂波信号非平稳特性的一个重要体现，它表现为随机分布在不同距离、不同角度上的零星的运动或者静止目标，但与一般目标不同，它们具有较为强烈的回波起伏特性。由于海尖峰出现时间较短，使得海杂波由稳态向非稳态，非时变向时变转换，体现出微多普勒特性，雷达有可能将海尖峰判断为一个具有一定速度的机动目标，进而导致虚警概率的增加。因此，采用微多普勒理论对它进行深入研究，分析其对海杂波的影响是非常必要的。现有文献多是对海尖峰的定性描述和研究，对其进行的系统分析还很欠缺。M. Greco等人对海尖峰的统计特性进行了分析，认为幅度门限、最小间隔时间和最小尖峰宽度是描述海尖峰的3个重要因素，给出了海尖峰的判定方法，但是3个因素的确定仅通过统计分析得到，具有不确定性。图1(a)给出了IPIX雷达19931107_135603数据在HH极化方式下的海尖峰判定情况，图中红色实线表示判别为海尖峰的海杂波数据，其它的蓝色虚线背景表示非海尖峰的海杂波数据。为了方便分析海尖峰特性，将海尖峰和背景海杂波分离，分析两者的时频分布，如图1(b)和图1(c)所示，可以明显看出海尖峰幅度高于背景海杂波幅度，且频率分布不同，具有时变特性。

3.2海杂波多普勒特性分析

海杂波的多普勒谱特征反映了海面本身的动态特性，一方面依赖于雷达工作参数，另一方面和引起散射现象的海洋环境参数密切相关，主要包括极化、频率、雷达相对风向的观测角度、擦地角、海况、波浪速度及波浪类型等。众多学者从雷达实测数据分析和随机粗糙面散射理论两方面对海杂波多普勒谱特性进行了大量的研究。然而，前者仅通过大量的数据统计得出经验模型，未从理论上对多普勒谱频移及展宽机理进行分析；后者针对的是特定背景或环境，粗略的假设与实际海面不符，不能很好地反映真实海面的时变性和非平稳特征，而且所提出的越来越复杂的建模方法带来的是实时性的急剧降低或者缺乏可实现性。对于“慢变信号”引起的Bragg散射，通过传统的Fourier变换(Fourier Transform, FT)得到海面散射回波的时频分析，能够给出特定时间和特定频率范围的能量分布；对于“快变信号”产生的非Bragg散射，回波信号频率随时间发生变化，若仍采用Fourier变换不能很好地反映和提取频率的变化信息。

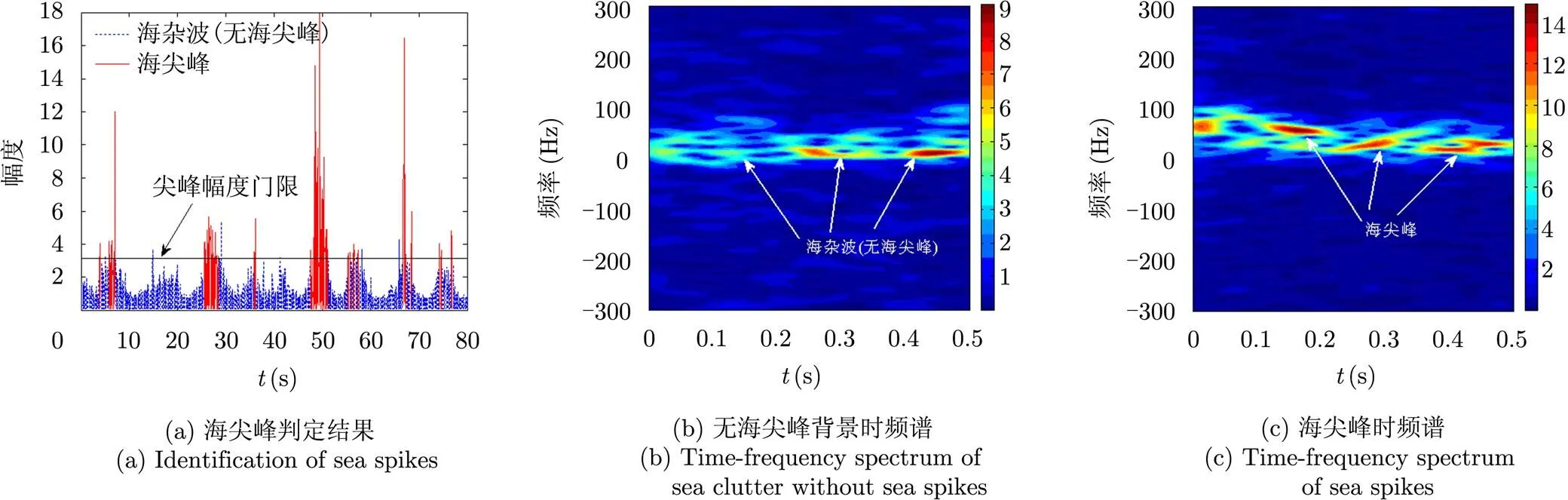
图1 IPIX雷达数据海尖峰判别及时频分析(19931107_135603)

时频分析方法是研究时变、非平稳信号的有力工具，作为时间和频率的2维函数，时频分布给出了特定时间和特定频率范围的能量分布，也描述了非平稳信号的频率随时间变化的过程，适于分析海杂波的多普勒特性并应用到弱目标检测中。主要方法包括基于FT的谱相减法、基于短时Fourier变换(Short Time Fourier Transform, STFT)和Wigner- Vill变换(Wigner-Vill Distribution, WVD)的峰值估计法、平滑伪WVD法(Smoothed Pseudo WVD Distribution, SPWVD)、小波变换(Wavelet Transform, WT)和自适应chirplet分解法等，各种方法的基本原理和性能比较如表1所示。然而，由于海杂波信号往往表现为非高斯、非平稳、时变、多分量信号，经典的时频变换方法和滤波方法有很大的局限性。尤其是高海况时，海面起伏变得剧烈、粗糙，海杂波的幅度和多普勒均随时间变化，“快变信号”产生非Bragg谱使得多普勒的中心频率偏移或展宽，降低了雷达目标的检测性能。近年来，人们开始研究新的变换方法研究海杂波特性，并用于弱目标检测。

表1基于经典时频分析的海杂波的多普勒分析方法比较

Tab. 1 Comparison of Doppler analysis methods of sea clutter based on classical time-frequency representation

分数阶Fourier变换(FRactional Fourier Transform, FRFT)作为一种统一的时频变换，将信号分解在一组正交的Chirp基上，更适于分析或处理时变的非平稳信号，能够反映多普勒的变化规律。与常用二次型时频分布不同的是FRFT采用单一变量表示时频信息，降低了运算量，又是一种线性变换，没有交叉项干扰。文献[4,23]采用FRFT积累动目标回波信号能量，用于解决海杂波中背景下的目标检测问题，结果表明，在FRFT域能够很好地反映海杂波的时变特性。图2给出了IPIX雷达19931107_135603纯海杂波数据的FRFT谱分布，可见，海杂波在FRFT域幅值起伏变化剧烈，频率较高，在变换阶数=1(频域)周围能量分布相对集中，但海杂波也具有微弱变化的加速度，能够很好地体现和描述较高海况情况下海杂波中的非Bragg散射回波特性。FRFT算法从不同程度上对非平稳信号的时变性给予了恰当的描述，弥补了Fourier分解的不足，但仍属于全局分析的范畴，究其原因在于基函数决定了对信号的分析能力。1998年，Huang等人提出了一种基于经验的模式分解算法(Empirical Mode Decomposition, EMD)和基于Hilbert变换的时频谱图，即Hilbert-Huang变换(Hilbert-Huang Transformation, HHT)，具有优秀的时频分辨性能。EMD是基于数据时域局部特征的，它能将复杂信号分解成若干个具有不同频率的固有模态函数(Intrinsic Mode Function, IMF)，得到由信号瞬时频率和瞬时幅值构成的完整时频谱，从而使瞬时频率具有实际的物理意义。由于分解是基于信号时域局部特征的，因此分解是自适应的，特别适合分析非平稳、非线性随机过程。文献[36,37]采用HHT分析雷达目标和海杂波信号，进行了初步探讨。采用EMD方法，对海杂波幅值信号进行筛选，可获得其IMF, IPIX雷达的19931118_023604和19931118_162658纯海杂波幅值经过EMD分解后得到的IMF如图3所示，()表示原始海杂波的幅值信号，(),,()表示海杂波的各个IMF, IMF成份的频率从()到()依次降低，故利用EMD可在时域内将信号按频率高低进行分解，由于IMF每一时刻仅包含单一频率成份，因此，通过Hilbert变换可以得出各IMF分量的时频图，定量地描述时间与频率的关系。而STFT和WT等方法只能定性地描述时间和频率的关系，而不能定量、精确地描述时间与频率的关系。

4 海面微动目标回波信号建模及检测研究现状

海面目标特性分析与建模是目标检测的一项重要内容，不过与海杂波特性分析相比，基于雷达实测回波数据的目标特性研究相对较少，原因在于，实际雷达观测条件下难以获得只有目标信号的回波数据。目前应用较多的目标模型是起伏模型，包括Swerling起伏模型 (也称为Rayleigh起伏)、Rice起伏模型、起伏模型、对数正态起伏模型以及Nakagami起伏模型等。然而，起伏模型仅从统计角度对目标的幅度起伏特征进行建模，不能反映海面目标随海面颠簸导致的姿态变化，引起的雷达回波功率的调制效应。因此，众多国内外学者从实际出发，对运动目标及其运动特性进行建模：一是海面运动目标的雷达回波幅度建模，包括运动目标电磁散射特性、回波的幅度调制、本身形状、大小等静态几何参量的确定；二是对海面目标运动特征的建模，即描述目标在海面上的运动方程。

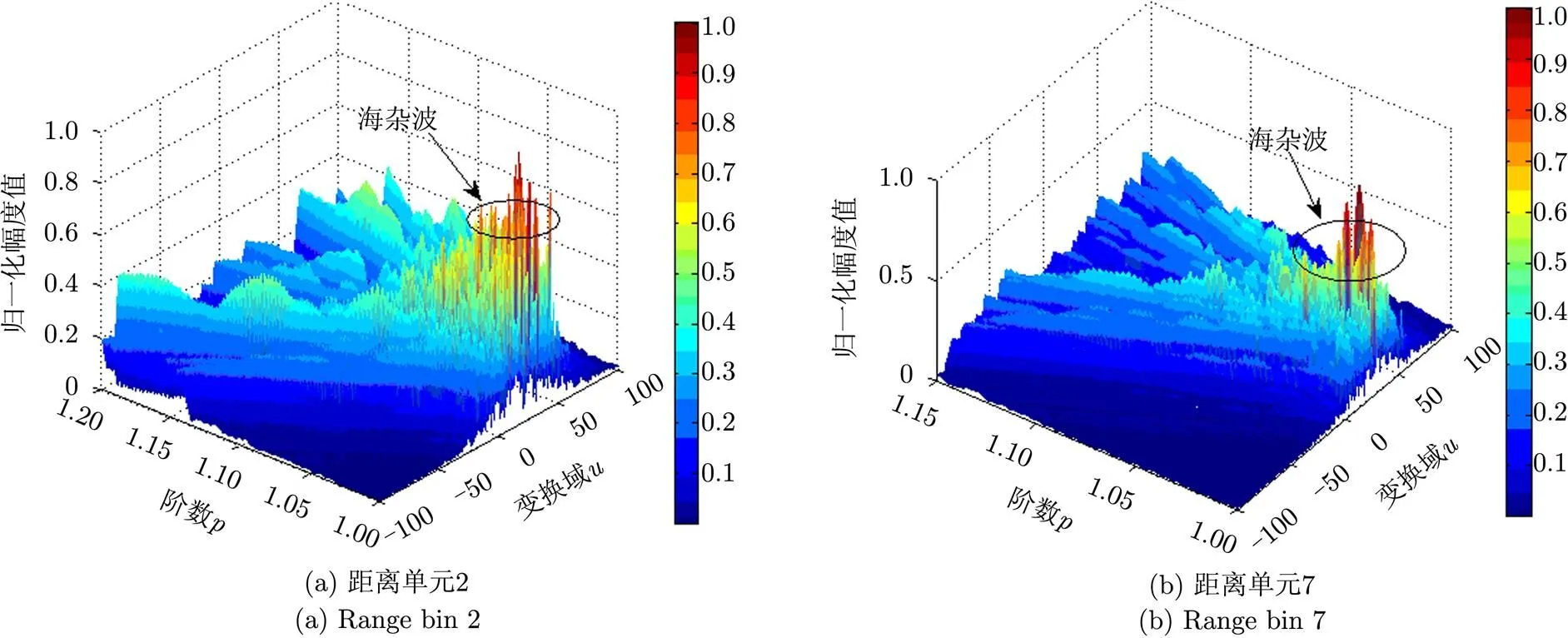
图2 IPIX雷达海杂波数据的FRFT谱(19931107_135603)

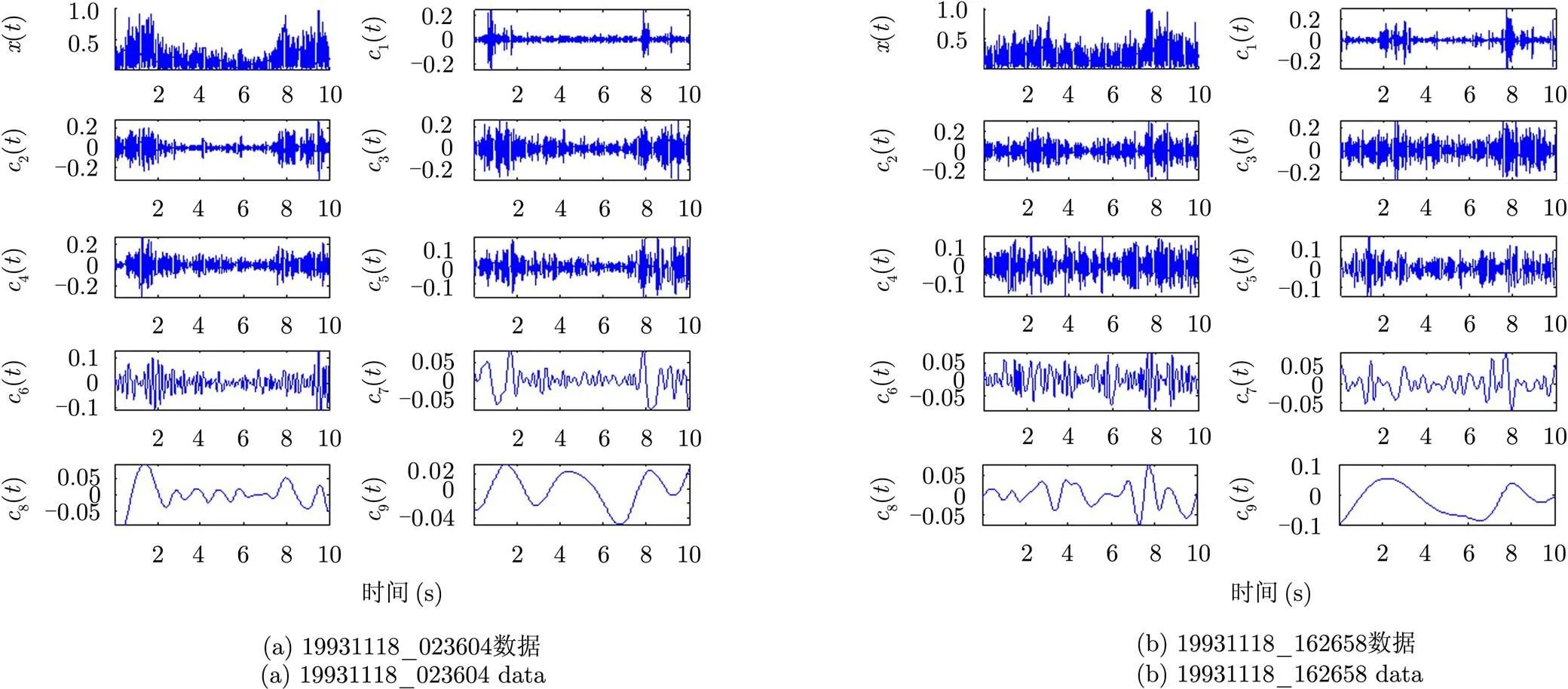
图3 IPIX雷达海杂波数据幅值的IMF

4.1海面微动目标回波信号建模

4.1.1海面目标电磁散射特性建模 对海面目标的电磁散射特性的建模是一项非常复杂的工作。首先，从舰船目标本身考虑，由于其具有很大的电尺寸及复杂的结构，电磁散射机理十分复杂；其次，海表面是时变的，由于其波浪起伏使得海面成为巨大的粗糙表面，时变海面对电磁波的反射也随时间变化；再次，海面舰船目标同海面之间的电磁耦合十分复杂，加之海面与舰船之间的相互作用使得舰船在海面的姿态不断变化，因而海面舰船目标的电磁散射计算问题变得更为复杂。Victor C. Chen研究了微动目标的雷达后向散射特性，指出目标微动对电磁波具有回波功率调制特征，可根据微动目标的RCS时间序列反演微动规律，提取目标微动信息，从而为研究微动目标的回波功率调制特性奠定了理论基础。2010年，Ángel F等人首次基于ISAR图像和微动特征分析刚体和非刚体运动目标的雷达后向散射特性，并通过仿真的舰船、直升机和人体验证算法，能够提取目标的微多普勒信息。由此可见，通过计算微动目标的电磁散射特性，研究目标复杂运动对雷达回波的RCS调制作用，能够进一步揭示目标姿态变化引起的散射强度变化特性，从而更好地分析和提取微动特征。

4.1.2海面目标运动建模 在海面目标运动建模方面，国内外许多学者从多种角度进行了研究，运动模型也经历了由简单到复杂，由单散射目标到多散射目标，由刚体到非刚体，由平动到转动，由周期运动到非周期运动，由时域到频域再到变换域等几个主要研究阶段。传统的对海面运动目标的建模仅认为目标在3维空间中平动，即舰船在运动过程中，坐标系的各坐标轴永远相互平行，表现为匀速运动、匀加速运动和变加速运动等，根据Weierstrass近似原理，其回波信号可由足够阶次的多项式相位信号近似表示，而运动状态比较复杂的目标在一段短的时间范围内，常可用线性调频(Linear Frequency Modulation, LFM)信号作为其一阶近似。基于此模型，文献[45]研究了两种海杂波背景下的微弱匀加速运动目标的检测方法，在最大程度保留目标信号能量的同时尽量地抑制海杂波，达到低信杂比下有效地检测出海面运动目标的效果，但算法的通用性不强。由于舰船随海面波动而产生颠簸，一方面，在高海况条件下，海杂波的存在降低了回波信号的信杂比；另一方面，舰船姿态变化复杂，不仅存在平动，舰船还绕参考点作3轴转动以及天线的转动，导致散射点的多普勒频率随时间非线性变化。引起的姿态变化包括舰船以其前进方向为轴作滚动，以在水平面内与前进方向垂直的方向为轴作俯仰运动，在由船身确定的平面内以塔台的方向为轴作偏航运动等3种运动形式，如图4所示。根据微多普勒的定义，海面舰船目标的微动表现为平动中的非匀速运动、3轴转动以及天线的转动。由此可见，传统的海面目标平动模型在复杂的海洋环境和日益提高的目标检测要求下，越来越显得捉襟见肘，主要体现为目标模型难以描述转动运动形式以及对目标运动状态的时变性、周期性考虑不足等。

目前，对舰船目标的3轴转动的研究主要集中于ISAR舰船成像方面，对于岸基高分辨雷达观测海面舰船却少有报道。ISAR对舰船成像依靠舰船与雷达视线之间的相对转动，它由舰船航行和海浪作用下舰船自身摇摆产生的转动组成。只有首先了解舰船运动的特点，才能更有效地设计出合适的ISAR成像技术和算法。邢孟道等人对外场舰船目标进行了ISAR成像试验，分析表明由于海水波动等原因，使舰船作3维运动，散射点子回波为调幅-调频信号(Amplitude Modulation-Frequency Modulation, AM-FM)，在一定程度上，可近似为调幅-线性调频(AM-LFM)信号，或者近似分段的AM-LFM信号，则对舰船目标的瞬时成像问题转化为噪声和杂波背景下的多分量AM-LFM信号瞬时参数估计问题。针对多分量的AM-FM信号给信号的参数估计带来的极大困难，人们相继提出了基于自适应Chirplet分解、匹配傅里叶变换(Matching Fourier Transform, MFT和Chirp傅里叶变换(Chirp Fourier Transform, CFT)的舰船目标ISAR成像方法。然而，已有的文献并未详细推导舰船的3维转动与AM-FM信号参数的对应关系，也没有考虑复杂运动情况下的微动特征，难以对时变的多普勒分量进行分析和提取。

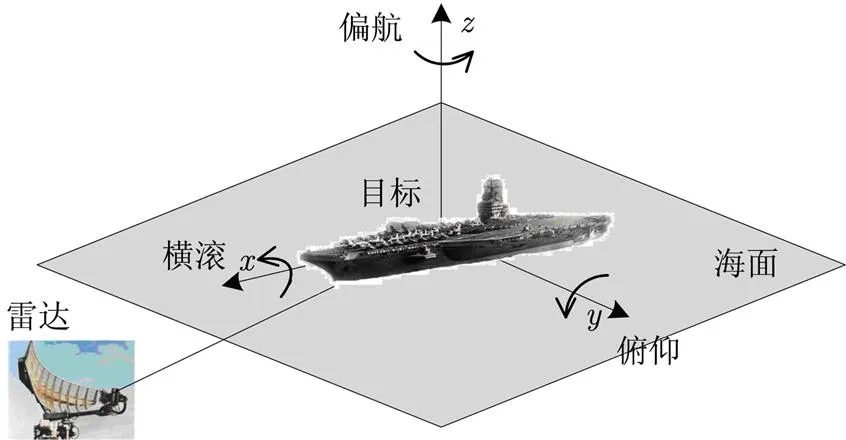
图4 雷达观测海面目标几何关系图

4.2目标微动特征分析与检测方法

微动本质上是一种非匀速运动或周期运动，微动目标雷达回波受到调制，其多普勒随时间非线性变化，称为一类频率调制的时变信号。微多普勒信号具有非线性和非平稳的特点，同时微动目标回波一般为多分量信号，因此，微动目标雷达特征分析和提取以非平稳、时变信号、多分量信号处理技术为主要工具。

4.2.1基于Fourier变换的频谱分析方法 基于FT的频谱分析方法是最早用于微多普勒信号分析的工具，人们相继提出了利用多普勒谱宽和多普勒谱峰值比的振动振幅和相位估计方法、包络检测法、多谐波微多普勒信号分析方法以及循环平稳特征调制相位信号参数估计方法等，并应用于医学成像、高速公路上车辆检测、进动弹头回波分析以及噪声抑制等方面。然而，频谱分析方法为一种全域变换，缺乏时间局域性，不能有效处理时变的非平稳微多普勒信号。

4.2.2经典时频分析方法 时频分析方法被广泛用于微多普勒的特性分析以及微动特征提取与参数估计。第一类为线性时频表示，如STFT, WT和Gabor变换等，线性时频分布无交叉项，但受不确定原理的制约，时频分辨率较低；另一类为非线性时频表示，主要包括Cohen类时频分布，如WVD等。目前，基于Cohen类方法分析微多普勒信号存在以下不足：(1)非线性频率调制信号或多元信号的时频分布中存在交叉项影响；(2)典型的微动目标雷达回波模型为多分量正弦调频信号(Sinusoidal Frequency-Modulated, SFM)，其相位是无限阶可导的，因此采用WVD处理SFM信号不能得到理想的时频聚集性；(3)通常微动信号是微弱的调频信号，而Cohen类方法对信杂比要求较高，从而影响参数估计的准确性。

微多普勒信号的特点要求信号分析方法应具有低交叉项、高时频分辨率和大动态范围的特点，以便更好地揭示目标微多普勒特征。从本质上说，微多普勒是由于目标运动引起的多普勒频移，因此，微多普勒信号处理也即对调频信号的处理。在这种情况下，国内外学者开始从其它方向寻找解决该问题的有效途径。

4.2.3相位匹配分析方法 相位匹配处理方法是根据微多普勒信号的形式，设计与其相对应的指数基函数，并将微多普勒信号在此基函数上进行分解。根据不同基函数形式可设计出不同的基函数分解方法，例如MFT、自适应Chirplet分解法(线性调频小波基函数分解法)和正弦调频基函数分解法等。MFT使用的变换因子是一组正交函数集，故不存在多分量信号交叉项的影响。Chirplet分解与时频变换、FT等方法相比，能够方便地实现信号在二阶相位上的分解与重构。正弦调频基函数分解法采用调频基函数提取振动或旋转频率以及微多普勒成分的相位信息，不需要信号成分的个数，但需已知微多普勒信号的最大瞬时频移。Victor C. Chen指出独立成分分析(Independent Component Analysis, ICA)技术更适合分析具有空间局域性的微多普勒谱图特征，他提出了时空联合独立成分分析(Spatial-temporal ICA)，将2维空间ICA推广至3维时间-空间域，可将微多普勒谱分解为对应信号不同微动特征的基函数的线性组合。由于微动信号在一定程度上可近似为AM-LFM信号，而FRFT对LFM有良好的能量聚集性和检测性能，同时根据分段信号长度自适应地选择FRFT的长度，可近似得到阶段的微动信号，达到分析和提取微多普勒信号的目的。目前，少有文献将FRFT作为微多普勒信号分析的工具，主要受限于FRFT缺少时域定位的功能。为此，陶然等人在FRFT中加入滑动的短时窗函数，得到短时FRFT(Short-Time FRFT, STFRFT)，通过窗函数的滑动完成整个时间上的信号局部性质分析，可得到在任意时刻的该段信号的频率变化，极大地扩展了FRFT的应用范围。随着国内外学者对FRFT理论的研究不断深入，这种新的时频分析工具必定成为分析微多普勒信号的理想手段。

4.2.4参数模型分析方法 信号时频处理方法可分为非参数模型法和参数模型法两大类。上述方法均为非参数模型法，其作为微多普勒特征分析工具具有不可比拟的优势，但估计性能受时频分辨率的限制。而对目标微动特征进行参数化估计，在建立目标微动参数估计模型的基础上，仅需要求解最优模型参数，便能较好地分析和提取微动特征。目前，基于参数模型的微多普勒信号分析的研究尚处于起步阶段，研究的方法主要有时变参数模型法和基于稀疏表示的参数估计模型法。时变参数模型法是近年来应用于非平稳随机信号分析与处理的一种新方法，其优点在于将非平稳时变问题转化为平稳的线性时不变问题，进一步提高了参数估计的精确度，其中具有代表性的是时变自回归(Time- Varying AutoRegression, TVAR)模型法。研究表明，单分量AM-FM信号可由一阶TVAR模型表示，多分量AM-FM信号可由高阶TVAR建模，因此，TVAR模型适用于对微动目标回波进行参数化建模和估计。基于时频分析的参数估计方法可以看作将信号在时频基函数上的分解，如果信号的特性与分解的基函数相匹配，就可以采用某几个基函数的组合来表示原始信号，即信号可以被稀疏表示。基于时频分析的方法的基本思想是将信号在一组完备的时频基上展开，而如果将能够很好地刻画信号局部时频结构的时频原子构成的过完备字典替代完备基函数，使得信号的自适应表示称为可能，则参数估计问题转化为信号的稀疏表示问题，并且对频率具有超分辨能力，从而更有利于获得目标精细特征。目标雷达回波可视为少数强散射中心回波的叠加，回波具有稀疏特性，因此，采用稀疏表示的方法分析微动信号，并进行参数估计是非常适合的。

5 研究展望

由国内外研究现状可知，微多普勒理论在精细雷达特征信号处理中具有良好的表现，可以很好地刻画信号本身的频率变化。微动目标的RCS调制从功率上描述了微动目标雷达特征，表征了目标姿态的变化。海面目标的非匀速平动和3轴转动导致散射点的多普勒频率随时间非线性变化，因此，海面目标的微动特征能够反映目标的雷达回波调制特性、几何结构和运动特征，同时展示了时间、空间、频率3维特征空间的变化特性。这些均为微多普勒理论在对海雷达回波信号分析中的应用提供了很好的基础与借鉴。从现有研究状况分析，未来研究中需要进一步解决的问题包括以下几个方面。

5.1海杂波建模及特性分析方面

随着高分辨力雷达的发展，对海面微弱目标的检测与识别成为可能。但在低掠射角及高海况的条件下，“快变信号”(海尖峰)导致海面起伏变剧烈、粗糙，其产生的非Bragg谱导致多普勒的中心频率频移或展宽，海面回波信号表现出时变特性。此时，海面回波信号已不能采用传统的双尺度模型建模。经典时频变换方法和滤波方法有很大的局限性，很少考虑各个因素之间的相互作用(包括雷达的工作状态(入射角、发射频率、极化、分辨率等)，以及背景状况(如海况，风速、风向等))，也没有揭示出海杂波产生的物理机制。目前尚未有学者从微多普勒的角度对海杂波进行建模和特性分析，而海杂波的“三非”特性(非线性、非平稳、非高斯)，与微动信号特征存在相似性，但也有不同。采用微动信号分析方法对海杂波建模，能够更好地揭示海杂波的起伏特性及频率特征，充分掌握海杂波的特征信息，一方面，从海表面运动特性的角度出发，研究白浪、破碎波的姿态变化对雷达回波信号的调制作用(RCS调制和相位调制)；另一方面，根据海尖峰的微动特性，建立相应的微多普勒谱模型，并研究微多普勒谱的偏移和展宽特性，从而为海杂波抑制和微弱目标检测提供必要的先验信息。

5.2海面微动目标回波建模及特性分析方面

舰船等微动目标在海面上将产生由转动引起的姿态变化包括偏航、滚动和俯仰3种周期运动，这3种转动之间可能同时存在，而且，由于受非线性策动力和非线性阻尼力的作用，3维转动都呈现出随机性和多倍周期的特点，海面的波动起伏以及海面反射引起的多径效应，使得舰船姿态变化较为复杂。此时，需要分别研究海面刚体目标和非刚体目标的运动特征，由简单到复杂，由一维到多维，由仅考虑目标到同时考虑目标和海面起伏，建立海面微动目标回波模型。对微动特征的提取和识别是建立在微动的散射中心和微动物体本身一致的假设基础上的，然而，随着观测角度的变化，微动散射中心也随之变化，频率变化不满足正弦调频的形式，以上这些因素都会对海面微动目标的建模造成困难，有待于进一步研究。同时，在微动目标特性分析方面，应分别从理论模型和实测数据两方面分析海杂波和微动目标的微多普勒特性，寻找回波信号的微多普勒区域，从时域、极化域、变换域和稀疏域多个角度进行分析，扩展数据的利用维度，判定信号是否具有微动特性，目的在于充分掌握海杂波及海面目标的微动特征信息，为后续的微动目标检测、特征提取与参数估计打下基础。

5.3微多普勒信号特征分析和检测方面

目前，国内外对雷达目标微动特征的分析和研究还主要集中在点目标微多普勒方面，在对微动引起的雷达信号调制效应分析方面，如电磁波、RCS、时域、变换域和极化域调制等，还未见系统的阐述。通过建立完善的雷达目标微动特征体系，将会为雷达目标的检测和识别提供新的途径。微多普勒是估计目标微动参数的前提，关键在于瞬时频率的高精度估计和提取。微动特征的提取集中于微动参数估计，并未考虑微动目标姿态变化对回波产生的影响，联合微动参数估计和散射强度变化引起的周期性调制效应等，可揭示更加丰富的目标微动特征信息。目前，国内外对微多普勒信号的分析方法主要应用了非平稳信号处理方法如时频分析等，而在时频分辨率、多分量信号分析、对信噪比的要求以及鲁棒性等方面，经典的时频分析方法有待改进。FRFT, HHT及其改进方法和基于参数模型的微多普勒信号分析方法(时变参数模型法和稀疏表示法)为微动目标的精细描述提供了新的途径，但其理论体系仍还不够完善，在参数估计精度及算法计算量方面还存在不足。另外，由于舰船目标的转动速度比较慢，要观测到精细的微多普勒信息需要较长的积累时间，而长时间里会产生较大的高阶相位项。并且在长相参积累时间内也常会出现跨距离单元的问题，导致目标信号能量无法有效积累。因此，多目标、长时间积累、距离徙动条件下微动特征增强与提取方法仍需进一步研究。

6 结束语

本文着眼于微多普勒理论在非平稳信号处理领域中的应用，回顾了微多普勒的研究发展历程，总结了动态海面散射杂波建模方法和海杂波多普勒特性分析方法，重点介绍了微多普勒在海面微动目标检测中的应用现状、主要技术途径、发展前景以及当前存在的问题。通过对其发展历程和应用场景的回顾与总结，可以发现微多普勒理论已在海杂波建模和目标检测领域中发挥着重要作用，是继多普勒理论后又一重要的信号分析方法。微多普勒拓展了信号利用的维度，可提取更多有用的信息，因此还可以用于目标识别和成像等领域。可以预期，微多普勒技术的成熟和发展将弥补已有方法的不足，能够进一步提升雷达目标探测和识别能力。

[1] Ward K D and Watts S. Use of sea clutter models in radar design and development[J].,&, 2010, 4(2): 146-157.

[2] Haykin S, Bakker R, and Currie B W. Uncovering nonlinear dynamics: the case study of sea clutter[J]., 2002, 90(5): 860-881.

[3] Greco M, Stinco P, and Gini F. Identification and analysis of sea radar clutter spikes[J].,&, 2010, 4(2): 239-250.

[4] Guan Jian, Chen Xiao-long, and He You. Adaptive fractional Fourier transform-based detection algorithm for moving target in heavy sea clutter[J].,&, 2012, 6(5): 389-401.

[5] Chen V C, Li Fa-yin, Ho Shen-shyang,.. Micro-Doppler effect in radar: phenomenon, model, and simulation study[J]., 2006, 42(1): 2-21.

[6] Chen V C, Li F, Ho S S,.. Analysis of micro-Doppler signatures[J].-,, 2003, 150(4): 271-276.

[7] Renhorn I, Karlsson C, and Letalick D. Coherent laser radar for vibrometry: robust design and adaptive signal processing[C]. Proceedings of SPIE, 1995, 2472: 23-30.

[8] 陈行勇. 微动目标雷达特征提取技术研究[D]. [博士论文], 国防科学技术大学, 2006: 20-22.

Chen Xing-yong. Research on radar signature extraction from target with micro-motions[D]. [Ph.D. dissertation], National University of Defense Technology, 2006: 20-22.

[9] Thayaparan T, Abrol S, Riseborough E,.. Analysis of radar micro-Doppler signatures from experimental helicopter and human data[J].,&, 2007, 1(4): 289-299.

[10] Cai Cheng-jie, Liu Wei-xian, Jeffrey Shiang Fu,.. Radar micro-Doppler signature analysis with HHT[J]., 2010, 46(2): 929-938.

[11] Philip Gatt, Henderson S W, Thomson J A,.. Micro- Doppler lidar signals and noise mechanisms: theory and experiment[C]. Proceedings of SPIE, 2000, 4035: 422-435.

[12] Gene Greneker, Jon Geisheimer, and David Asbell. Extraction of micro-Doppler data from vehicle targets at X-band frequencies[C]. Proceedings of SPIE, 2001, 4374: 1-9.

[13] Lemnios W Z and Grometstein A A. Overview of the Lincoln Laboratory ballistic missile defense program[J]., 2002, 3(1): 9-32.

[14] Anderson M G and Rogers R L. Micro-Doppler analysis of multiple frequency continuous wave radar signatures[C]. Proceedings of SPIE, 2007, 6547: 65470A.

[15] Alessio Balleri, Karl Woodbridge, and Kevin Chetty. Frequency-agile non-coherent ultrasound radar for collection of micro-Doppler signatures[C]. IEEE Radar Conference, Washington D.C., USA, May 2011: 23-27.

[16] 庄钊文, 刘永祥, 黎湘. 目标微动特性研究进展[J]. 电子学报, 2007, 35(3): 520-525.

Zhuang Zhao-wen, Liu Yong-xiang, and Li Xiang. The achievements of target characteristic with micro-motion[J]., 2007, 35(3): 520-525.

[17] 黄孟俊, 陈建军, 赵宏钟, 等. 海面角反射器干扰微多普勒建模与仿真[J]. 系统工程与电子技术, 2012, 34(9): 1781-1787.

Huang Meng-jun, Chen Jian-jun, Zhao Hong-zhong,.. Micro-Doppler modeling and simulating of corner reflector in sea surface[J]., 2012, 34(9): 1781-1787.

[18] Li Kai-ming, Liang Xian-jiao, Zhang Qun,.. Micro- Doppler signature extraction and ISAR imaging for target with micromotion dynamics[J]., 2011, 8(3): 411-415.

[19] 高红卫, 谢良贵, 文树梁, 等. 基于微多普勒分析的弹道导弹目标进动特性研究[J]. 系统工程与电子技术, 2008, 30(1): 50-52.

Gao Hong-wei, Xie Liang-gui, Wen Shu-liang,.. Research on precession of ballistic missile warhead based on micro- Doppler analysis[J]., 2008, 30(1): 50-52.

[20] Bai Xue-ru, Zhou Feng, Xing Meng-dao,.. High resolution ISAR imaging of targets with rotating parts[J]., 2011, 47(4): 2530-2543.

[21] Jeong-Won Park and Joong-Sun Won. An efficient method of Doppler parameter estimation in the time–frequency domain for a moving object from TerraSAR-X data[J]., 2011, 49(12): 4771-4787.

[22] Zhang Min, Chen Hui, and Yin Hong-cheng. Facet-based investigation on EM scattering from electrically large sea surface with two-Scale profiles: theoretical model[J]., 2011, 49(6): 1967-1975.

[23] 陈小龙, 刘宁波, 宋杰, 等. 海杂波FRFT域分形特征判别及动目标检测方法[J]. 电子与信息学报, 2011, 33(4): 823-830.

Chen Xiao-long, Liu Ning-bo, Song Jie,.. Fractal feature discriminant of sea clutter in FRFT domain and moving target detection algorithm[J].&, 2011, 33(4): 823-830.

[24] Marco Martorella, Fabrizio Berizzi, and Enzo Dalle Mese. On the fractal dimension of sea surface backscattered signal at low grazing angle[J]., 2004, 52(5): 1193-1204.

[25] Walker D. Experimentally motivated model for low grazing angle radar Doppler spectra of the sea surface[J].-, 2000, 147(3): 114-120.

[26] Chen Xiao-long, Wang Guo-qing, Huang Yong,.. Study on the fractional power spectrum of the scattered echoes from 1-D time-varying sea surface[C]. Asia-Pacific Conference on Antennas and Propagation, Singapore, August 2012: 321-322.

[27] Guan Jian, Liu Ning-bo, Huang Yong,.. Fractal Poisson model for target detection within spiky sea clutter[J]., 2013, 10(2): 411-415.

[28] Farina A, Gini F, Greco M V,.. High resolution sea clutter data statistical analysis of recorded live data[J].,, 1997, 144(3): 2808-2811.

[29] Wang Yun-hua, Guo Li-xin, and Wu Zhen-sen. Modified two-scale model for electromagnetic scattering from the non-Gaussian oceanic surface[J]., 2005, 22(11): 2808-2811.

[30] Allan N, Trizna D B, and McLaughlin D J. Numerical comparison of techniques for estimating Doppler velocity time series from coherent sea surface scattering measurements[J].-,, 1998, 145(6): 367-373.

[31] Yasotharan A and Thayaparan T. Time-frequency method for detecting an accelerating target in sea Clutter[J]., 2006, 42(4): 1289-1310.

[32] Hao Yan-ling, Tang Yan-hong, and Zhu Yi. A combined denoising algorithm approach to sea clutter in wave monitoring[C]. 2nd International Symposium on Intelligent Information Technology Application, Shanghai, China, December 2008: 99-103.

[33] Zhang Y, Qian S, and Thayaparan T. Detection of a maneuvering air target in strong sea clutter via joint time-frequency representation[J].,&, 2008, 2(3): 216-222.

[34] 陶然, 邓兵, 王越. 分数阶傅里叶变换及其应用[M]. 北京: 清华大学出版社, 2009, 第2章.

Tao Ran, Deng Bing, and Wang Yue. Fractional Fourier Transform and Its Applications[M]. Beijing: Tsinghua

University Press, 2009, Ch. 2.

[35] Huang N E, Zheng S, Steven R,.. The empirical mode decomposition and the Hilbert spectrum for nonlinear non-stationary time series analysis[J].,&, 1998, 454(1971): 903-995.

[36] 关键, 张建. 基于固有模态能量熵的微弱目标检测算法[J]. 电子与信息学报, 2011, 33(10): 2494-2499.

Guan Jian and Zhang Jian. Weak target detection based on intrinsic mode energy entropy[J].&, 2011, 33(10): 2494-2499.

[37] 张建, 关键, 董云龙, 等. 基于局部Hilbert谱平均带宽的微弱目标检测算法[J]. 电子与信息学报, 2012, 34(1): 121-127.

Zhang Jian, Guan Jian, Dong Yun-long,.. Weak target detection based on the average bandwidth of the partial Hilbert spectrum[J].&, 2012, 34(1): 121-127.

[38] Derakhtian M, Khaliliazad Z, Masnadi Shirazi M A,.. Generalized likelihood ratio test-based multiple-target detection for fluctuating targets with unknown parameters[J].,&, 2011, 5(6): 613-625.

[39] Chen V C. Doppler signatures of radar backscattering from objects with micro-motions[J]., 2008, 2(3): 291-300.

[40] Ángel F García-fernández, Omar A Yeste-Ojeda, and Jesús Grajal. Facet model of moving targets for ISAR imaging and radar back-scattering simulation[J]., 2010, 46(3): 1455-1467.

[41] Guan Jian and Zhang Xiao-li. Subspace detection for range and Doppler distributed targets with Rao and Wald tests[J]., 2011, 91(1): 51-56.

[42] Lei Peng, Sun Jin-ping, Wang Jun,.. Micromotion parameter estimation of free rigid targets based on radar micro-Doppler[J]., 2012, 50(10): 3776-3786.

[43] Chen Xiao-long, Guan Jian, and He You. Sea clutter suppression and moving target detection method based on clutter map cancellation in FRFT domain[C]. CIE International Conference on Radar, Chengdu, China, October 2011: 438-441.

[44] 郭海燕, 董云龙, 关键. 基于分数阶模糊函数的海面运动弱目标检测[J]. 系统工程与电子技术, 2011, 33(6): 1212-1216.

Guo Hai-yan, Dong Yun-long, and Guan Jian. Weak target detection in sea clutter based on fractional ambiguity function[J]., 2011, 33(6): 1212-1216.

[45] 关键, 李宝, 刘加能, 等. 两种海杂波背景下的微弱匀加速运动目标检测方法[J]. 电子与信息学报, 2009, 31(8): 1898-1902.

Guan Jian, Li Bao, Liu Jia-neng,.. Two approaches of detecting weak moving target with constant acceleration in sea clutter[J].&, 2009, 31(8): 1898-1902.

[46] Li Y, Wu R, Xing M D,.. Inverse synthetic aperture radar imaging of ship target with complex motion[J].,&, 2008, 2(6): 395-403.

[47] 邢孟道, 保铮. 外场实测数据的舰船目标ISAR成像[J]. 电子与信息学报, 2001, 23(12): 1271-1277.

Xing Meng-dao and Bao Zheng. ISAR ship imaging of real data[J].&, 2001, 23(12): 1271-1277.

[48] 王勇, 姜义成. 基于自适应Chirplet分解的舰船目标ISAR成像[J]. 电子与信息学报, 2006, 28(6): 982-984.

Wang Yong and Jiang Yi-cheng. The ISAR imaging of ship based on adaptive Chirplet decomposition[J].&, 2006, 28(6): 982-984.

[49] 黄雅静, 曹敏, 付耀文, 等. 基于匹配傅里叶变换的匀加速旋转目标成像[J]. 信号处理, 2009, 25(6): 864-867.

Huang Ya-jing, Cao Min, Fu Yao-wen,.. ISAR imaging of equably accelerative rotating targets based on matching Fourier transform[J]., 2009, 25(6): 864-867.

[50] Wu Liang, Wei Xi-zhang, Yang De-gui,.. ISAR imaging of targets with complex motion based on discrete chirp Fourier transform for cubic chirps[J]., 2012, 50(10): 4201-4212.

[51] Huang S, Lerner R M, and Parker K J. On estimating the amplitude of harmonic vibration from the Doppler spectrum of reflected signals[J]., 1990, 88(6): 2702-2712.

[52] Greneker E F and Sylvester V B. Use of the envelope detection method to detect micro-Doppler[C]. Proceedings of SPIE, 2003, 5077: 167-174.

[53] 苏婷婷, 孔令讲, 杨建宇. 基于多谐波微多普勒信号分析的目标摄动参数提取方法[J]. 电子与信息学报, 2008, 30(11): 2646-2649.

Su Ting-ting, Kong Ling-jiang, and Yang Jian-yu. Target parameters extracted from multi-harmonic micro-Doppler signal analysis[J].&, 2008, 30(11): 2646-2649.

[54] 霍凯, 李康乐, 姜卫东, 等. 基于循环平稳特征的正弦调制相位信号参数估计[J]. 电子与信息学报, 2010, 32(2): 355-359.

Huo Kai, Li Kang-le, Jiang Wei-dong,.. Parameters estimation of signals with sinusoid modulated phase based on cyclostationary character[J].&, 2010, 32(2): 355-359.

[55] 李开明, 李长栋, 李松, 等. 基于Gabor变换的微动目标微多普勒分析与仿真[J]. 空军工程大学学报(自然科学版), 2010, 11(1): 40-43, 94.

Li Kai-ming, Li Chang-dong, Li Song,.. Analysis and simulation for micro-Doppler information of micro-motion target based on Gabor transformation[J].(), 2010, 11(1): 40-43, 94.

[56] 张云, 姜义成. 基于匹配傅里叶变换的舰船目标成像算法[J]. 大连海事大学学报, 2009, 35(1): 47-52.

Zhang Yun and Jiang Yi-cheng. A method of ISAR ship imaging based on match Fourier transform[J]., 2009, 35(1): 47-52.

[57] Pawan Setlur, Moeness Amin, and Fauzia Ahmad. Analysis of micro-Doppler signals using linear FM basis decomposition[C]. Proceedings of SPIE, 2006, 6210: 62100M.

[58] Chen V C. Spatial and temporal independent component analysis of micro-Doppler features[C]. IEEE International Radar Conference, Virginia, USA, May 2005: 348-353.

[59] Tao Ran, Li Yan-lei, and Wang Yue. Short-time fractional Fourier transform and its applications[J]., 2010, 58(5): 2568-2580.

[60] Abramovich Y I, Spencer N K, and Turley M D E. Order estimation and discrimination between stationary and time- varying (TVAR) autoregressive models[J]., 2007, 55(6): 2861-2876.

[61] 李松, 朱丰, 刘昌云, 等. 基于压缩感知的弹道导弹微多普勒提取方法[J]. 电波科学学报, 2011, 26(5): 990-995.

Li Song, Zhu Feng, Liu Chang-yun,.. Extraction of micro-Doppler of ballistic missile based on compressive sensing[J]., 2011, 26(5): 990-995.

[62] Guo Jin-ku, Zou Hong-xing, Yang Xiao-jun,.. Parameter estimation of multicomponent chirp signals via sparse representation[J]., 2011, 47(3): 2261-2268.

[63] Ma Liang, Liu Jin, Wang Tao,.. Micro-Doppler characteristics of sliding-type scattering center on rotationally symmetric target[J]., 2011, 54(9): 1957-1967.

[64] Xu Jia, Yu Ji, Peng Ying-ning,.. Radon-Fourier transform for radar target detection, I: generalized Doppler filter bank[J]., 2011, 47(2): 1186-1202.

Applications and Prospect of Micro-motion Theory in the Detection of Sea Surface Target

Chen Xiao-long Guan Jian He You

(Department of Electronic and Information Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China)

Micro-Doppler signature is one of the physical characteristics of the target. The radar signature of a target with micro-motion can make fine characterizations of the shape, structure, and moving state of target, which reflects the nonstationary property of a radar signal. Hence, it has great superiority in the analysis of sea clutter and target detection in the case of high sea states based on the micro-Doppler theory. In this paper, to show the need for micro-Doppler, the modeling of scattering clutter from time-varying sea surface and analysis methods of sea clutter Doppler are first reviewed based on the principles and characteristics of micro-Doppler. Then, applications and technological approaches of micro-Doppler in sea surface target detection are introduced from the perspective of micro-motion target modeling and detection methods of micro-motion signatures. Finally, future research interests are highlighted based on problems experienced in present studies.

Micro-motion; Micro-Doppler; Sea clutter; Target detection

TN957.51

A

2095-283X(2013)01-0123-12

10.3724/SP.J.1300.2013.20102

陈小龙(1985-)，男，山东省烟台市，2010年获海军航空工程学院信息与通信工程学科硕士学位，现就读于海军航空工程学院，博士研究生，海军航空工程学院研究生三队，主要研究方向为雷达信号处理，海杂波中微弱目标检测。获全军优秀硕士论文奖。E-mail: cxlcxl1209@163.com

关 键(1968-)，男，辽宁省锦州市，2000年获清华大学信息与通信工程学科博士学位，教授，博士生导师，海军航空工程学院电子信息工程系主任，主要研究方向为雷达目标检测与跟踪、侦察图像处理和信息融合。获全国优秀博士学位论文奖，新世纪百千万人才工程国家级人选。E-mail: guanjian96@tsinghua.org.cn

2012-12-17收到，2013-01-04改回；2013-01-09网络优先出版

国家自然科学基金资助项目(61002045, 61179017, 61201445)和“泰山学者”建设工程专项经费资助课题

关键 guanjian96@tsinghua.org.cn