一种基于持续运动模型的星载SAR几何校正方法

仇晓兰*①②③ 韩传钊① 刘佳音②③



一种基于持续运动模型的星载SAR几何校正方法

仇晓兰韩传钊刘佳音

(北京遥感信息研究所 北京 100192)(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)(中国科学院电子学研究所 北京 100190)

几何校正是星载SAR地面处理的重要环节，几何校正精度对SAR图像的应用有着至关重要的影响。该文分析了传统星载SAR几何校正中卫星“停-走”模型近似对几何定位精度的影响，建立了卫星持续运动模型下的距离多普勒方程，并提出了持续运动模型下校正方程的简化求解方法。仿真实验和北京地区实际数据几何校正试验验证了该方法的有效性和正确性。

SAR；几何校正；斜距多普勒模型；“停-走”近似；持续运动模型

1 引言

合成孔径雷达(Synthetic Aperture Radar, SAR)具有全天时、全天候对地观测的能力，而在军事、减灾、测绘等领域有着独特的应用优势。自20世纪50年代合成孔径的概念被提出以来，经过约60年的发展，SAR技术得到了长足的进步，在军事、民用等各个领域发挥着日益重要的作用。星载SAR由于不受国界限制、观测范围广、成像效率高，更成为各国对地观测发展的重点。图像几何校正是星载SAR数据处理的重要环节，只有通过几何校正，将SAR图像的每个像素赋予地理位置信息，SAR图像才能真正成为地理空间信息的载体，支撑后续的应用。SAR图像几何校正的精度对SAR图像应用效益的发挥有着至关重要的影响。

影响SAR几何定位精度的误差源很多，包括轨道位置速度测量误差、SAR系统时间误差、大气传输误差、地面高程误差等，针对这些误差的分析可以参见文献[1-4]。上述误差主要由测轨及SAR系统硬件等器件水平和外部条件决定，地面处理可以通过一些技术(如依赖地面控制点)进行缓解，但需付出较大的人力物力代价，因此通过提高器件水平来获得高几何定位精度成为星载SAR的发展重点之一。

除上述误差源外，另一个引入几何校正误差的环节是地面处理，包括成像处理和几何校正处理。其中，成像处理中非线性变标、模型参数修正等处理会使图像存在一定的可预知的畸变，通常成像算法研究会给出算法引入的畸变，并将畸变模型输入至几何校正系统，从而规避成像算法的影响。星载SAR几何校正方法的研究成果颇多，而针对这些方法引入误差的分析则很少。通常认为基于距离-多普勒模型的SAR图像几何定位方法是精确的，如方程求解正确，将不会引入额外的误差。实际上，上述星载SAR几何校正方法均基于传统的卫星“停-走”近似模型，即认为SAR在发射脉冲到完成该脉冲回波的接收期间是静止的，随后再运动到下一个位置进行下一个脉冲的发射和接收。实际中SAR是持续运动的，基于“停-走”近似的几何校正方法存在一定的误差，尤其在高轨道星载SAR中，该误差将更加明显。

为此，本文主要针对传统星载SAR几何校正方法“停-走”近似模型引入的误差进行详细的分析，提出了一种基于持续运动模型的几何校正方法，最后通过仿真和实际数据的处理实验验证了本文分析的正确性和方法的有效性。本文结构安排如下：第2节回顾了传统“停-走”模型下星载SAR几何校正方程；第3节分析了“停-走”模型近似引入的几何定位误差，并提出一种基于持续运动模型下的几何校正方法；第4节给出了仿真和实验结果；第5节总结全文。

2 “停-走”近似下的星载SAR几何校正模型

SAR具有测距和测多普勒频率的能力，并且能在距离维和多普勒频率维实现高分辨。SAR图像每个像素均蕴含了SAR天线到目标的距离信息和天线与目标之间相对运动的多普勒信息。在SAR“停-走”模型的假设下，SAR图像目标地面位置可由如下3个方程联立来确定：

(1) 距离方程

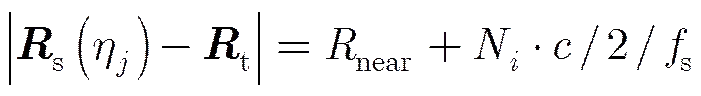
(2) 多普勒方程

(2)

(3) 地球模型方程

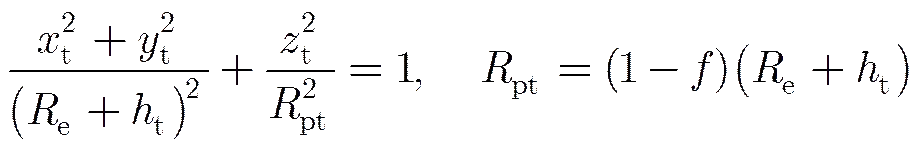
为简化方程形式，上述方程通常在地球固联坐标系下建立。其中：

(4)

(5)

3 持续运动模型下的星载SAR几何校正方法

在真实的持续运动模型下，脉冲的接收时刻滞后于脉冲发射时刻，在该段时间内卫星持续运动，故SAR卫星在脉冲发射时刻和接收时刻位置并不相同。在持续运动模型下，距离方程和多普勒方程应写为如下形式：

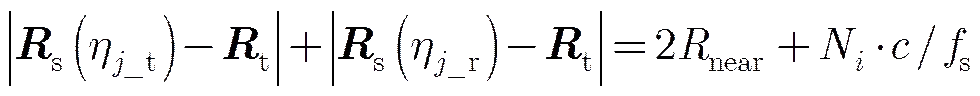
(7)

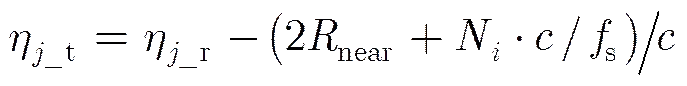
而目标的回波脉冲接收时刻则有：

(9)

于是：

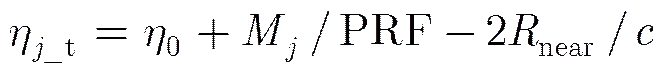
可见脉冲发射时刻与目标所处距离向像素位置无关，而脉冲接收时刻则与目标所处距离向像素位置有关，这与SAR成像的实际物理过程相吻合。

3.1“停-走”近似模型误差分析

基于上述方程，下面对传统“停-走”近似模型引入的几何定位误差进行分析。首先比较距离方程和。由于脉冲收发的时间间隔(2+/)/较短，设＝800 km，则上述时间间隔仅为约5 ms, SAR速度约为7000 m/s，该段时间间隔内卫星运动距离约为35 m。则：

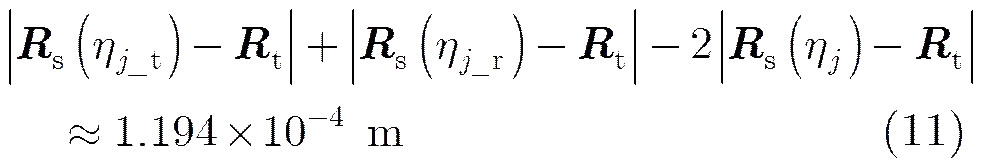
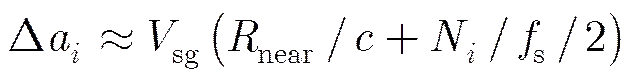
3.2持续运动模型下的几何校正方法

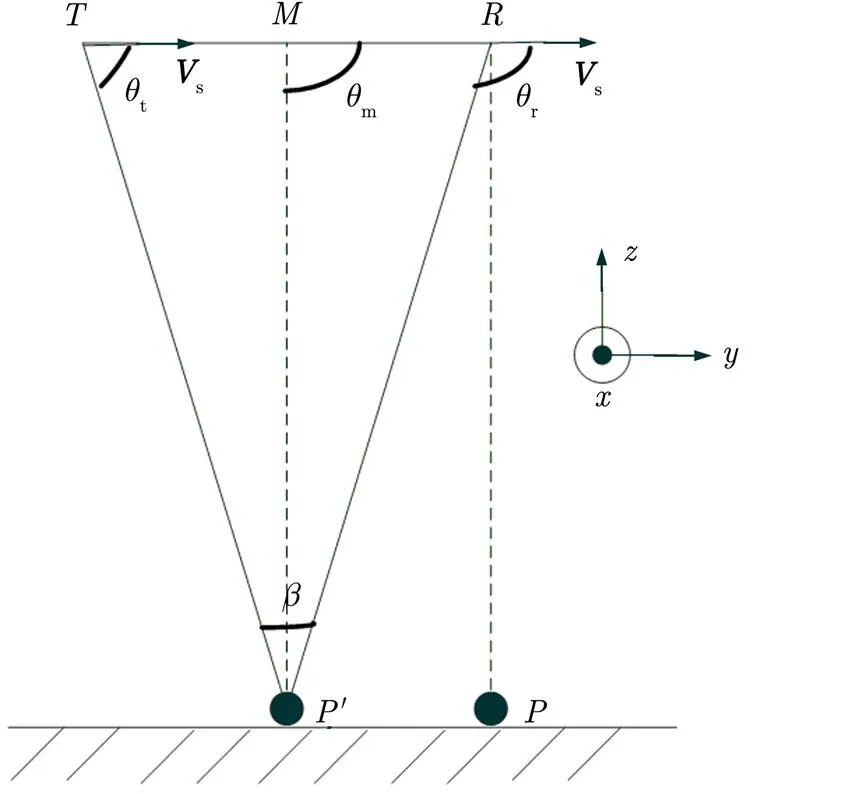
图1 “停-走”模型与持续运动模型多普勒方程求解示意图

由3.1节的分析，“停-走”模型对于距离方程的影响可以忽略，因此将距离方程直接简化成如下形式：

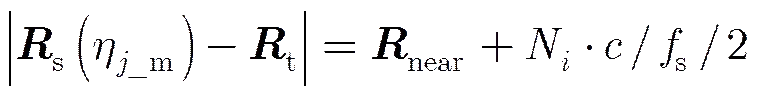
为了沿用传统校正方程的求解方法，将多普勒方程简化成如下形式：

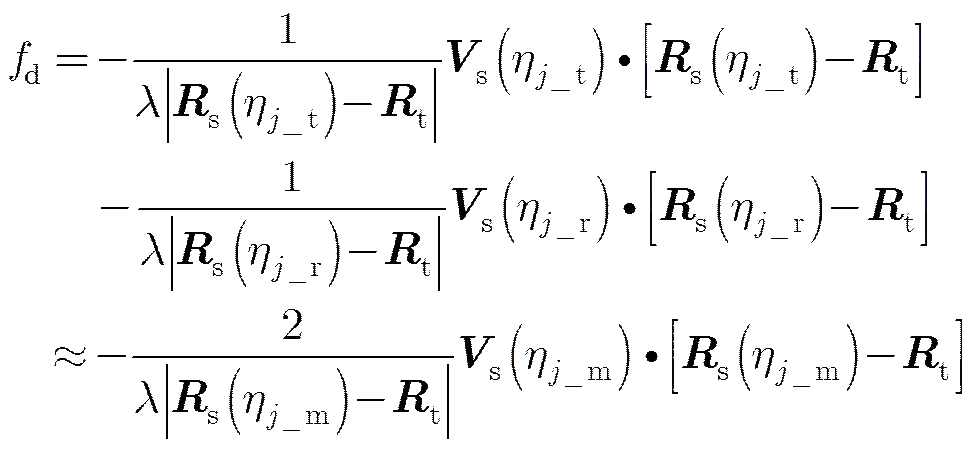
由于脉冲发射和接收之间的时间间隔为毫秒级，因此可以认为在此期间卫星为匀速直线运动，即。则方程式(14)可转换为

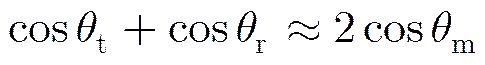
(16)

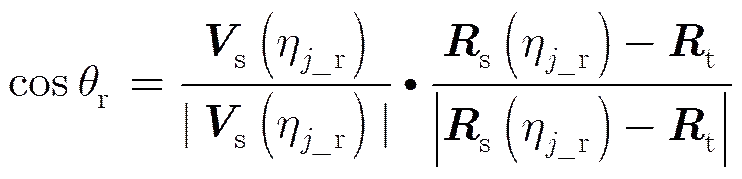
(18)

又

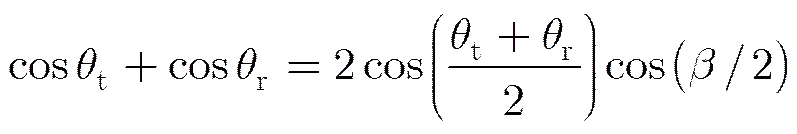
(20)

故

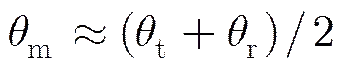
(22)

通过上述简化，星载SAR几何定位仍可沿用传统“停-走”近似模型下的求解方法，仅需将目标对应的方位时刻改变为脉冲收发时刻的中间时刻即可。

凭心而论，侯大同对汤翠的好那可是没说的。九年了，侯大同对汤翠，完全可以说是延续了他在寻找汤莲时的那种不顾一切的热诚，甚至更甚。套用一句时髦的广告词——没有最好，只有更好。洗衣做饭带孩子，就差没有替汤翠生孩子了。汤翠相信，若没有生理差别，侯大同一定愿意替汤翠受一个女人应该受的所有的苦。两口子，光有好肯定不够，汤翠老是觉得侯大同像一个昨天刚认识的陌生人，他身上机关暗道数不尽，你今天发现一个，明天又生出一个，后天，不一定哪儿又冒出一个来。汤翠有时候也想过，要是姐姐活着的话，自己兴许会嫁个同学，或者邻居。好歹，感情有个基础。

4 仿真分析与实验

为了验证上述分析的正确性和校正方法的有效性，下文首先对低轨星载SAR进行仿真实验，接着将该方法用于遥感卫星的实际数据处理，并给出实测结果。

4.1仿真实验

仿真参照RadarSAT-1系统设置参数并进行了适当的调整，如表1所示。

表1仿真参数

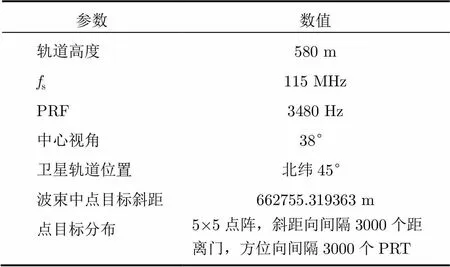
Tab. 1 Simulation parameters

在基于传统“停-走”近似模型下，点目标定位误差如图2所示，采用持续运动模型下简化距离-多普勒方程后，定位误差如图3所示。图2和图3中的像素位置通过对图像升采样64倍后确定，故目标像素位置精度为0.0156个像素。此外，图中目标编号规则为1～5号点为近距目标，对应方位时间依次递增，21～25号点为远距目标，以此类推。

由上述仿真结果可见，在传统的“停-走”模型近似下，SAR图像距离向定位误差几乎为零，沿方位向则存在约7.5个像素左右的误差，由此导致本仿真条件下存在约15 m的定位误差。此外，由图2可见，在传统“停-走”模型近似下，不同距离门的目标方位定位误差还存在约0.3 m变化。这一畸变与式(12)理论计算的结果一致：在本仿真条件下，卫星地速为7045.4 m/s，近距目标和远距目标相差12000个距离采样，因此，根据式(12)计算得到近距目标和远距目标之间方位定位误差差异为0.352 m，与仿真结果基本吻合，从而验证了分析的正确性。采用本文提出的持续运动模型简化方程后，方位向的几何定位误差得到了很好的消除，定位误差在0.2 m以内(见图3)。此外需要说明的是，本仿真结果中同一距离门的目标沿方位向存在0.1个像素以内规律性的几何定位误差，该误差由仿真系统中成像处理器引入，由于误差量级较小，未予以校正。

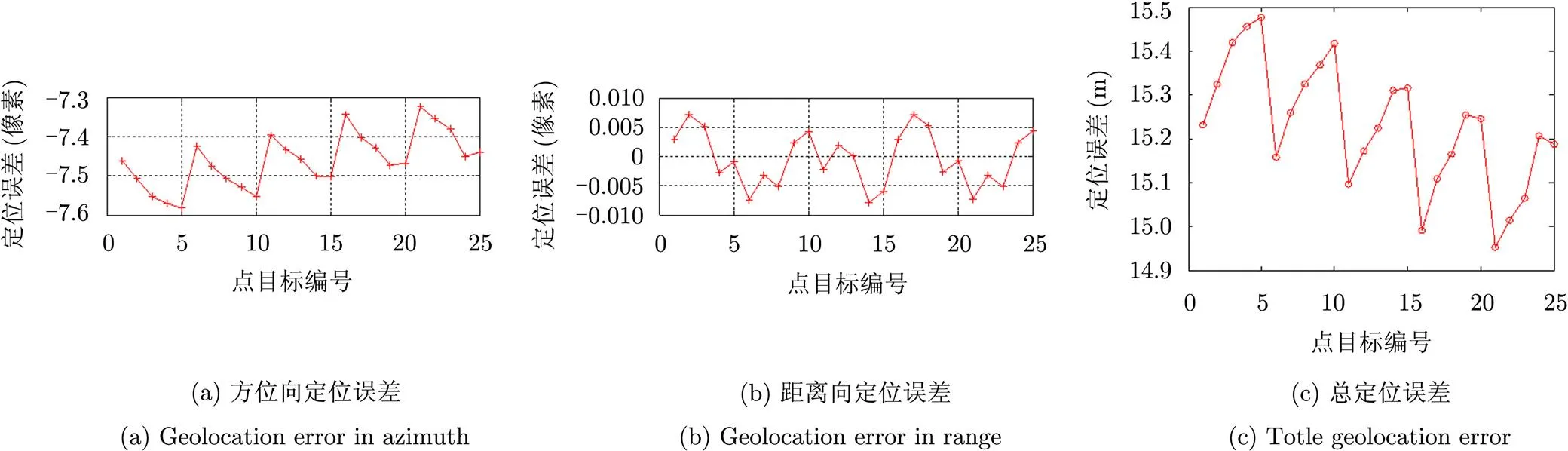
图 2 传统“停-走”近似模型下的定位误差

4.2实际数据几何校正实验

为了验证本文方法的有效性，对RadarSAT-1的两景北京地区SAR图像进行了几何校正实验，并在该地区用差分GPS实测了17个地面检查点进行检验，检验结果如图4、图5所示。采用本文的持续运动模型简化定位方程后，方位向定位误差明显减小，从而使得SAR图像几何定位精度有了显著的提高，证明了方法的有效性。

5 总结

本文针对传统几何校正中采用的“停-走”近似模型，分析了该近似引入的定位误差并给出了理论公式。在此基础上提出了基于持续运动模型的几何校正方程，提高了星载SAR几何定位精度，并通过分析给出了几何校正方程的简化形式，从而可以沿用传统的几何校正方法。仿真和实际数据处理实验验证了分析的正确性和方法的有效性。

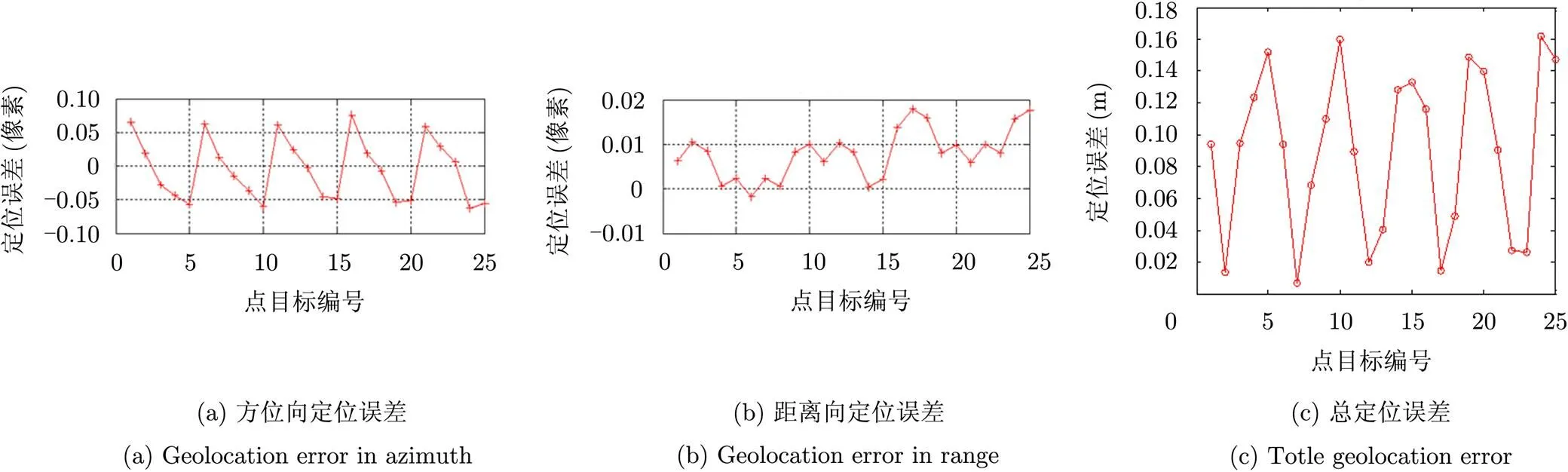
图 3 持续运动简化模型下的定位误差

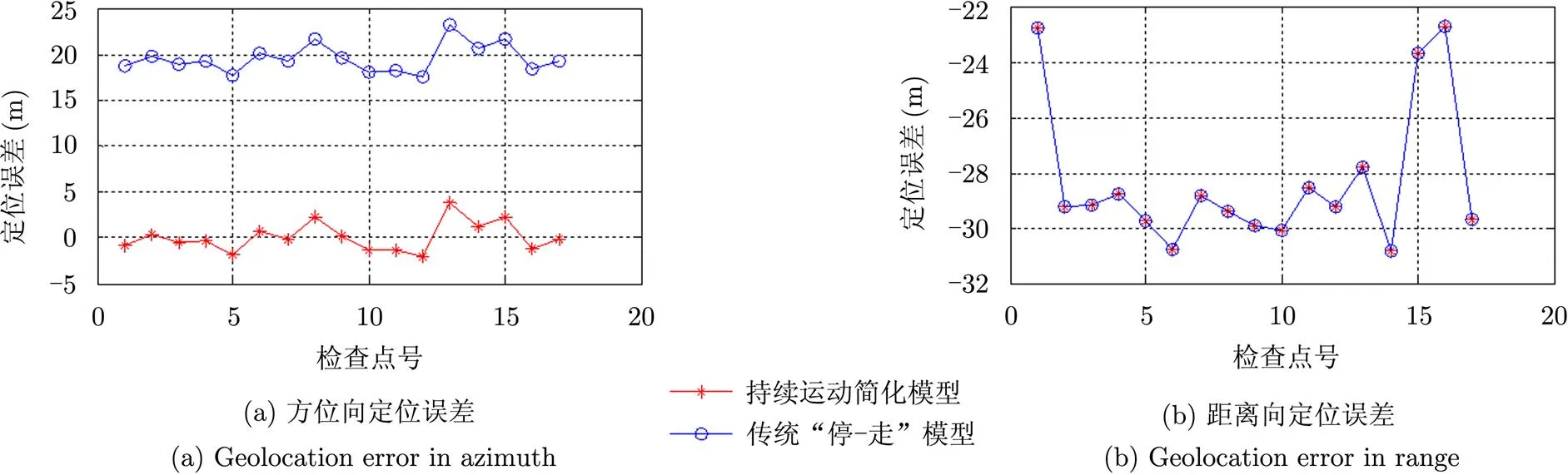
图4 第1景北京图像几何定位结果

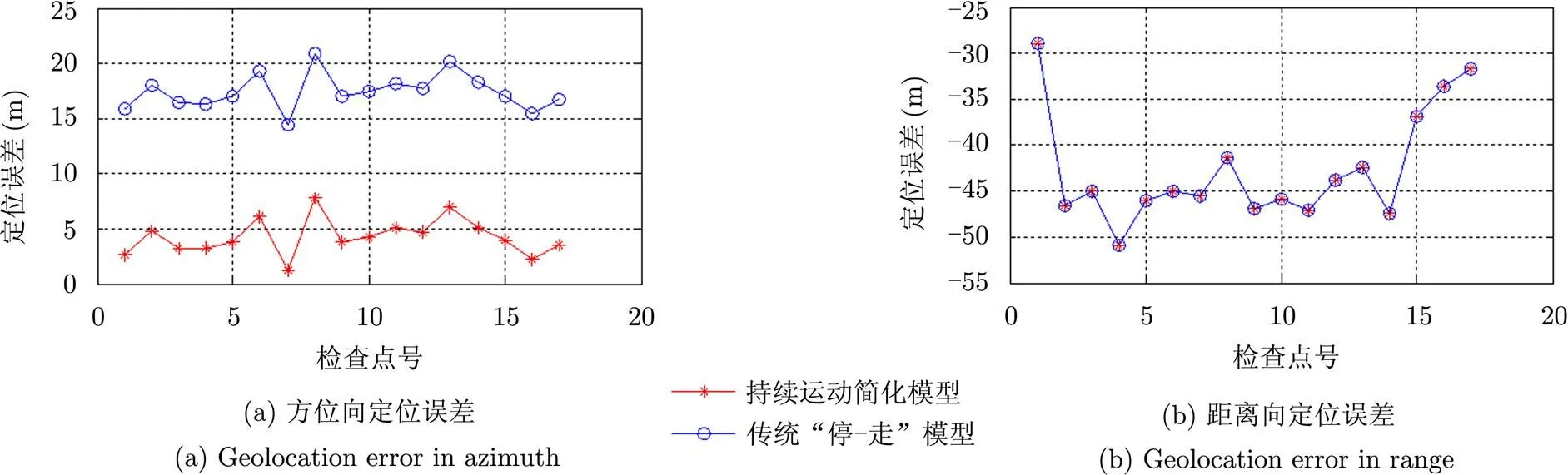
图5 第2景北京图像几何定位结果

[1] Curlander J C. Location of spaceborne SAR imagery[J]., 1982, 20(3): 359-364.

[2] Curlander J C. Utilization of spaceborne SAR data for mapping[J]., 1984, 22(2): 106-112.

[3] 魏钟铨. 合成孔径雷达卫星[M]. 北京: 科学出版社, 2001: 17-22.

Wei Zhong-quan. Synthetic Aperture Radar Satellite[M]. Beijing: Science Press, 2001: 17-22.

[4] 陈元藻. 合成孔径雷达卫星定位误差源分析[J]. 上海航天, 1998, (3): 16-21.

Chen Yuan-zao. Primary analysis of location error sources synthetic aperture radar satellite[J]., 1998, (3): 16-21.

[5] Qiu Xiaolan, Hu Donghui, and Ding Chibiao. An improved NLCS algorithm with capability analysis for one-stationary BiSAR[J]., 2008, 46(10): 3179-3186.

[6] Qiu Xiaolan, Hu Donghui, and Ding Chibiao. Non-linear chirp scaling algorithm for one-stationary bistatic SAR[C]. 1st Asian and Pacific Conference on Synthetic Aperture Radar (APSAR), Nov. 5-9, 2007: 111-114.

[7] 周金萍, 唐伶俐, 李传荣. 星载SAR图像的两种实用化R-D定位模型及其精度比较[J]. 遥感学报, 2001, 5(3): 192-197.

Zhou Jin-ping, Tang Ling-li, and Li Chuan-rong. Development of two practical R-D location model and precision comparison between them[J]., 2001, 5(3): 192-197.

[8] 刘秀芳, 刘佳音, 洪文. SAR图像地理编码处理流程的研究[J]. 遥测遥控, 2005, 26(4): 12-18.

Liu Xiu-fang, Liu Jia-yin, and Hong Wen. Research on the data flow of SAR geocoding[J]., 2005, 26(4): 12-18.

[9] 陈尔学, 李增元. ENVISAT ASAR影像地理定位方法[J]. 中国图象图形学报, 2004, 9(8): 991-995

Chen Er-xue and Li Zeng-yuan. Study on ENVISAT ASAR image geolocation method[J]., 2004, 9(8): 991-995.

[10] Liu Xin, Ma Hongbin, and Sun Weidong. Study on the geolocation algorithm of space-borne SAR image[C]. International Workshop on Intelligent Computing in Pattern Analysis/Synthesis (IWICPAS), Berlin, Germany, 2006: 270-280.

[11] Huang Lijia, Qiu Xiaolan, Hu Donghui,.. Focusing of medium-earth-orbit SAR with advanced nonlinear chirp scaling algorithm[J]., 2011, 49(1): 500-508.

[12] 李军, 邢孟道, 李亚超, 等. 同步轨道SAR参数分析及成像方法[J]. 系统工程与电子技术, 2010, 32(5): 931-936.

Li Jun, Xing Meng-dao, Li Ya-chao,.. Parametric analysis and imaging method of geosynchronous SAR[J]., 2010, 32(5): 931-936.

A Method for Spaceborne SAR Geolocation Based on Continuously Moving Geometry

Qiu Xiao-lanHan Chuan-zhaoLiu Jia-yin

(Beijing Institute of Remote Sensing Information, Beijing 100192, China)(Key Laboratory of Technology on Geo-spatial Information Processing and Application System,Chinese Academy of Sciences, Beijing 100190, China)(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)

Geolocation is a very important step in Synthetic Aperture Radar (SAR) data processing. The precision of geolocation severely affects the applications of SAR images. This paper analyzes the influences on SAR geolocation caused by the traditional “stop-go” approximation, and establishes the range-Doppler equations for the real continuously moving configuration. It also provides a simplified way of solving the equations. Simulations and geolocation experiments on real SAR data of the Beijing area validate the proposed method and show the correctness of the analysis.

Synthetic Aperture Radar (SAR); Geolocation; Range-Doppler model; “stop-go” approximation; Continuously moving configuration

TN959.72

A

2095-283X(2013)01-0054-06

10.3724/SP.J.1300.2013.20072

仇晓兰(1982-)，女，北京市遥感信息研究所在站博士后，中国科学院电子学研究所副研究员，主要研究领域为单/双站SAR成像技术、SAR几何校正技术、InSAR处理技术，出版专著一部，发表论文20余篇。E-mail: xlqiu@mail.ie.ac.cn

韩传钊(1971-)，男，博士，北京市遥感信息研究所研究员，主要研究领域为星载SAR系统技术。

刘佳音(1976-)，女，中国科学院电子学研究所在职博士研究生，主要研究领域为SAR几何定位技术。

2012-09-28收到，2012-11-28改回；2012-12-31网络优先出版

国家自然科学基金(61101200)资助课题

仇晓兰 xlqiu@mail.ie.ac.cn