广义双曲线分布在概化理论偏态数据方差分量估计中的应用

黎光明，张敏强

(1.华南师范大学心理应用研究中心，广州510631；2.广州大学教育学院心理系，广州510006)

0 引言

广义双曲线分布（简称GH分布），是Barndorff-Nielsen(1977)在研究丹麦海岸风积沙砾颗粒大小的分布时首次提出的，GH分布的密度函数(Eberlein&Hammerstein,2003;Mena&Walker,2007)[1，2]如下：

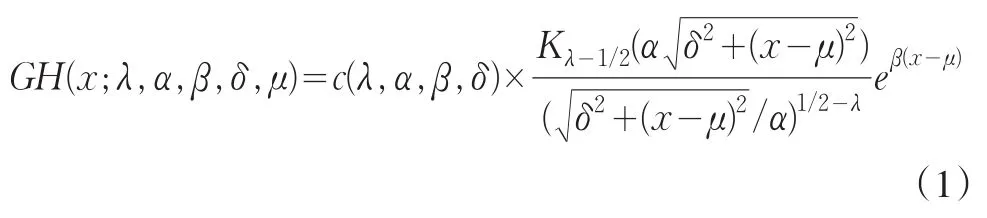
在公式（1）中，各参数的定义域如下：当λ＜0时，δ＞0， ||β ≤α；当 λ=0时，δ＞0， ||β ＜α；当 λ＞0时，δ≥0， ||β＜α。其中，Kv()是具有λ指数校正的Bessel函数，其函数可表达成：

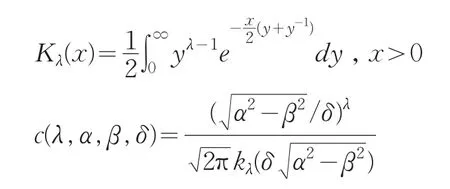
上述GH分布的密度函数也可表达成：

从公式（2）可知，GH分布的性质主要由5个参数决定，α和β分别决定分布的峰度和偏度，μ和δ分别决定密度函数的位置和形状，λ决定分布的尾部厚度[3]。

利用GH分布的性质，可以模拟不同分布的数据，包括偏态分布数据。对于偏态分布数据，在实践中具有常见性，这是因为随着社会的发展，心理与教育测量的应用领域发生了较大变化，被测群体的知识和能力等特质在一定程度上不再服从偏度为0的分布[4]。Othman(1995,p.8)[5]研究表明，许多测验数据的分布呈弱偏态，如CAP(California Assessment Program)和UCSB(University of California Santa Barbara)，这两个测验数据的分布偏度值介于-0.91～+0.85，如表1所示。

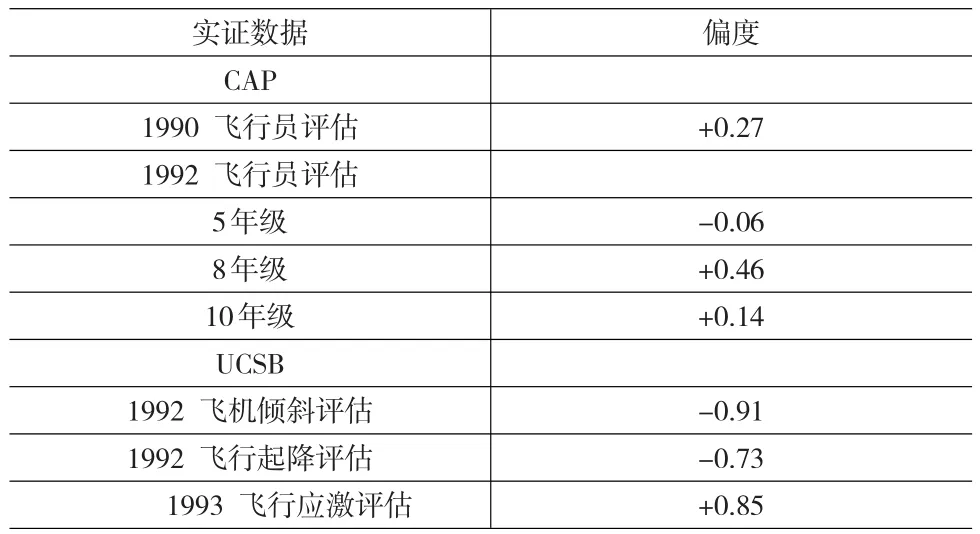
表1 飞行员表现性评价测验分数的偏度

概化理论（Generalizability Theory，GT）是关于行为测量可靠性的统计理论(Shavelson&Webb,1991,p.1)[6]。概化理论结合测量的情境关系(context of measurement situation)对CTT的笼统误差进行探查和分解，辨明不同的误差来源，并且在一定范围内变动测量的情境关系，以考察这种变动引起的误差的相对变化，从而达到对误差方差进行控制(Shavelson&Webb,1991)，因此概化理论又称为方差分量模型(Brennan,2000)[7]。

数据分布对概化理论方差分量估计可能产生影响。特别地，当数据为偏态分布时，适合于正态分布数据的方差分量估计方法不一定适合于偏态分布数据。虽然Othman(1995)已经考虑到数据分布具有（弱）偏态，但是Othman并没有进行偏态分布数据的方差分量估计的研究，显得不足。本文旨在探讨如何利用GH分布性质模拟生成偏态分布数据，其偏度如何影响概化理论的方差分量估计。

1 方法

1.1 数据产生

基于p×i设计概化理论模型，根据GH分布的性质使用蒙特卡洛数据模拟技术产生偏态分布数据。数据模拟所使用的软件为R软件。产生偏态分布数据过程如下：

第一，在R软件中调用Hyperbolic Dist软件包，使用hyperb Change Pars和rhy perb函数生成服从某种偏度的偏态数据。在使用rhyperb函数前，需要先用hyperb Change-Pars对参数进行转换，主要是因为GH分布有不同量纲系统，转换成能够识别的量纲系统是必需的，服从某种偏态的广义双曲线分布数据才能够正常产生(Scott,2009)[8]。

第二，因为仅需要产生服从一定偏度的偏态数据，所以对GH分布的参数进行控制，令 λ=1，μ=0，δ=1，α=3，仅改变 β 值，β 仅选取五个点：-2、-1、0、1、2。编制的程序证明，β具有以0为轴的对称性，即β=-2与β=+2的结果相近，β=-1与β=+1的结果相近，如表2所示。

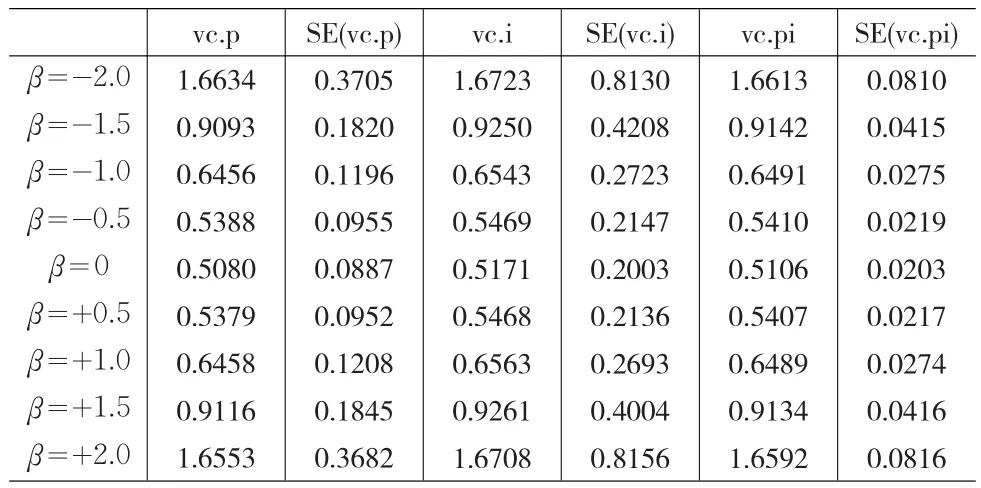
表2 不同偏态分布数据估计的方差分量及其标准误

在表2中，为了保持β值的连续性，β的取值为9个，即 β 为-2.0、-1.5、-1.0、-0.5、0、+0.5、+1.0、+1.5、+2.0。根据表2的数据结果，可得到图1。

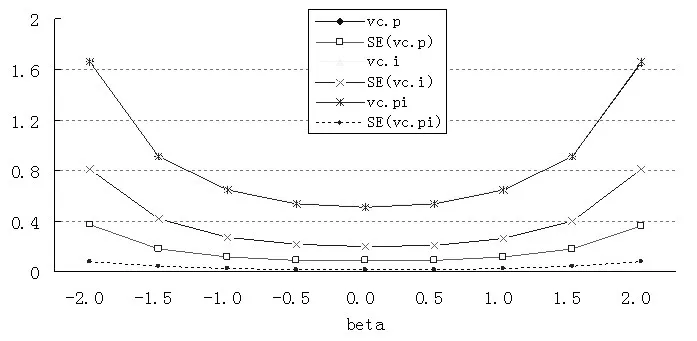
图1 不同偏态数据估计的方差分量及其标准误

从图1可以明显看出，方差分量具有以β=0为轴的对称性，这种对称性非常明显。因此，仅需生成β为-2、-1和0三种偏度的数据，并且令β为-2表示“高偏”，β为-1表示“中偏”，β为0表示“无偏”。

第三，在概化理论p×i设计下，将rhyperb函数生成的某个偏度下的三组偏态分布数据相加，即Xpi=μ+GH(p)+GH(i)+GH(pi)，这样，在概化理论模型下服从某种偏度的GH分布数据就可以产生。

第四，没有公式可以直接计算出偏态分布数据的三个方差分量参数，参考 Tong和 Brennan(2006,2007)[9，10]的做法，模拟5000批次数据，求取5000批次三个方差分量的平均数，用这两个估计值表示三个方差分量参数。

第五，针对某一个偏度值，生成的偏态分布模拟数据为矩阵数据（p×i），模拟次数为1000，这样可产生1000批次100×20的偏态分布模拟矩阵数据。β有三个偏度值（-2、-1和0），可以产生3×1000批次100×20的偏态分布模拟矩阵数据。

1.2 比较标准

1.3 分析工具

分析工具为R软件、WinBUGS软件、R2WinBUGS软件包、Coda软件包和HyperbolicDist软件包。借助这些软件或软件包，自编完成研究程序。

2 结果

2.1 三种偏态分布数据估计的人的方差分量

对β=-2、β=-1和β=0三种偏态分布数据，分别计算Traditional方法、Jackknife方法、Bootstrap方法和MCMC方法估计的人的方差分量，结果如表3所示。

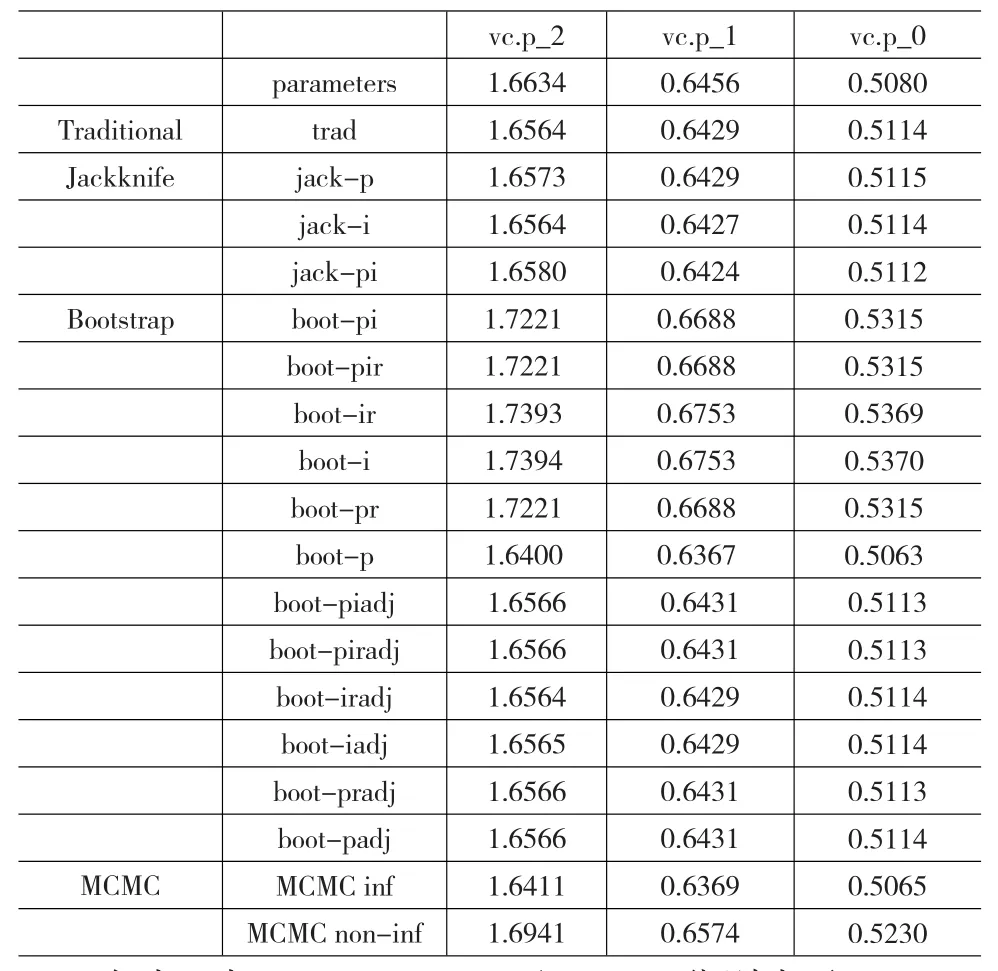
表3 三种偏态分布数据估计的人的方差分量

在表3中，vc.p_2、vc.p_1和vc.p_0分别表示 β=-2、β=-1和β=0偏态分布数据四种方法估计的人的方差分量。trad表示Traditional方法。Jackknife方法估计方差分量及其变异量时，需要考虑再抽样策略，这里仅使用jack-p、jack-i和jack-pi三种策略。Bootstrap方法也需要考虑再抽样策略，所考虑Bootstrap再抽样策略包括boot-p、boot-i、boot-pi、boot-pr、boot-ir和boot-pir。可以对Bootstrap方法进行校正，用后缀adj来表示校正的Bootstrap策略。MCMC inf表示有先验信息的MCMC方法，而MCMC non-inf则表示无先验信息的MCMC方法。的方差分量。其它表示符号及解释同表3。

2.2 三种偏态分布数据估计的题目的方差分量

对β=-2、β=-1和β=0的偏态分布数据，分别计算Traditional方法、Jackknife方法、Bootstrap方法和MCMC方法估计的题目的方差分量，结果如表4所示。

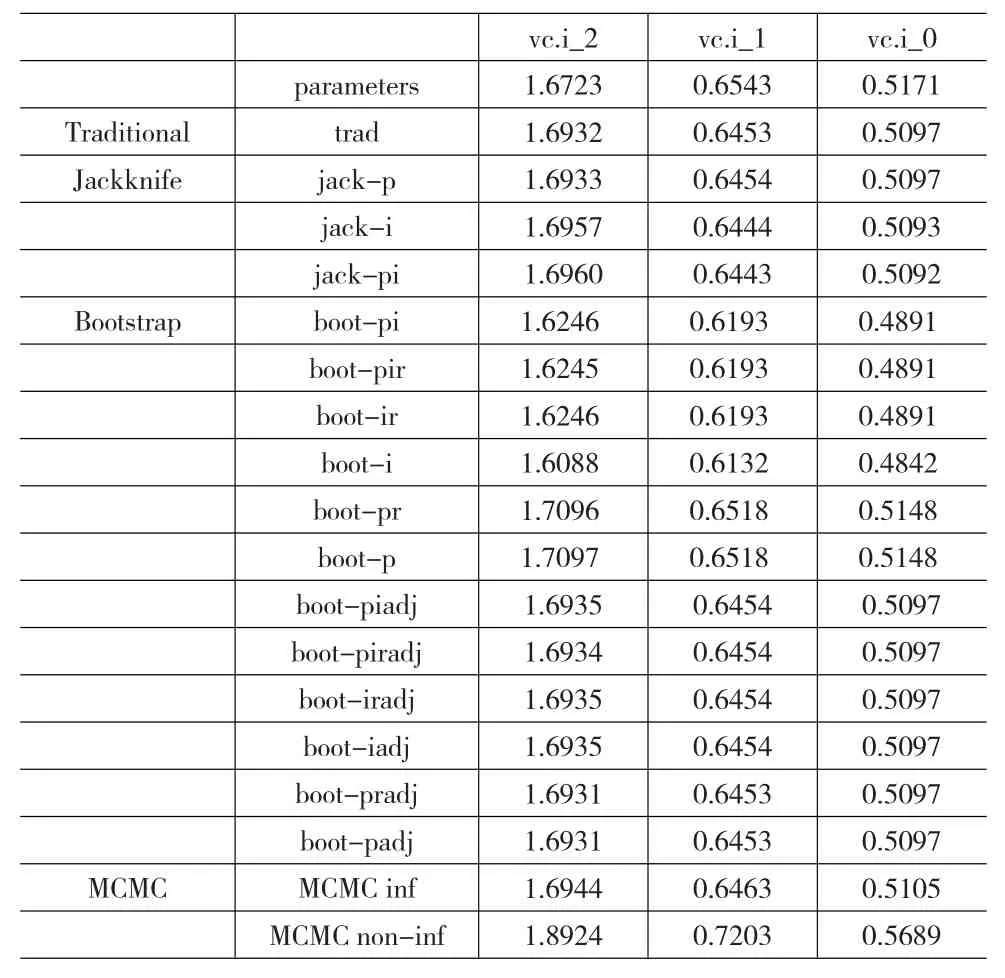
表4 三种偏态分布数据估计的题目的方差分量

在表4中，vc.i_2、vc.i_1和vc.i_0分别表示 β=-2、β=-1和β=0偏态分布数据四种方法估计的题目的方差分量。其它表示符号及解释同表3。

2.3 三种偏态分布数据估计的人与题目交互的方差分量

对β=-2、β=-1和β=0的偏态分布数据，分别计算Traditional方法、Jackknife方法、Bootstrap方法和MCMC方法估计的人与题目交互的方差分量，结果如表5所示。

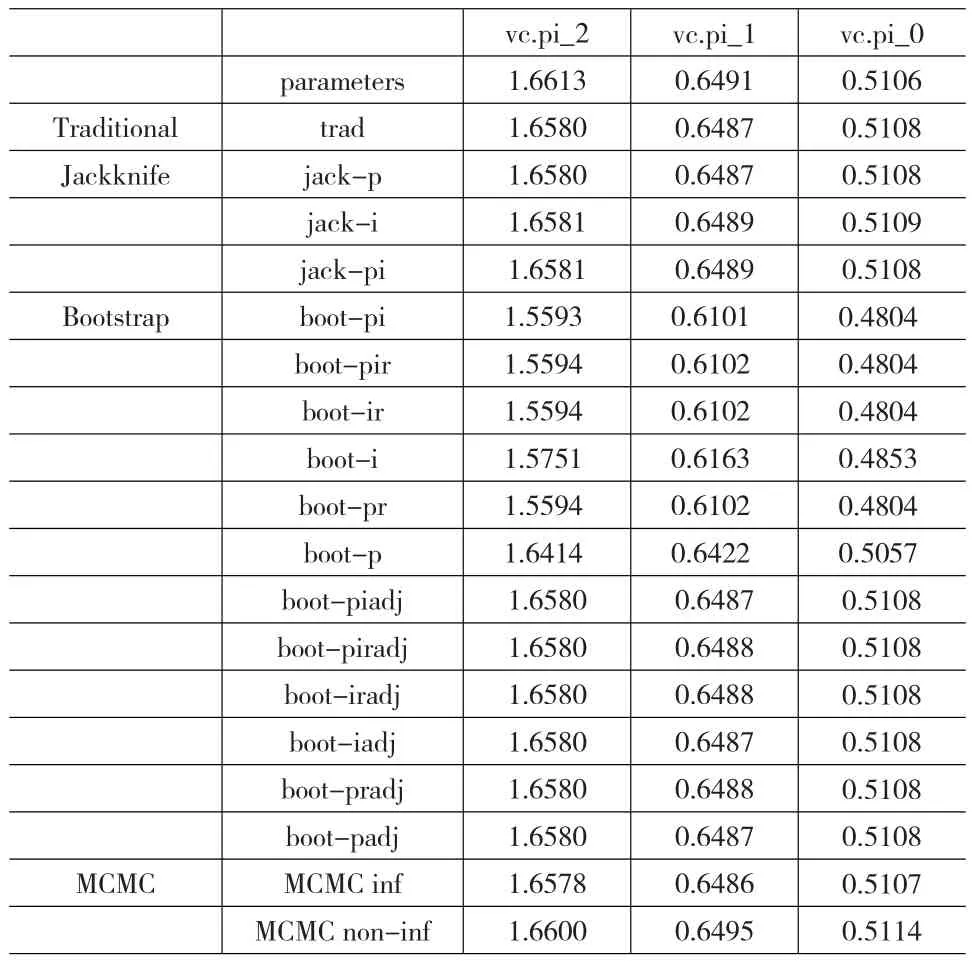
表5 三种偏态分布数据估计的人与题目交互的方差分量

在表5中，vc.pi_2、vc.pi_1和vc.pi_0分别表示β=-2、β=-1和β=0偏态分布数据四种方法估计人与题目交互

3 分析与讨论

3.1 三种偏态分布数据估计的人的方差分量偏差分析

根据表3中每种方法(或策略)估计的方差分量与参数的差值（bias），可以绘出三种不同偏态分布数据四种方法估计的方差分量偏差图，如图2所示。

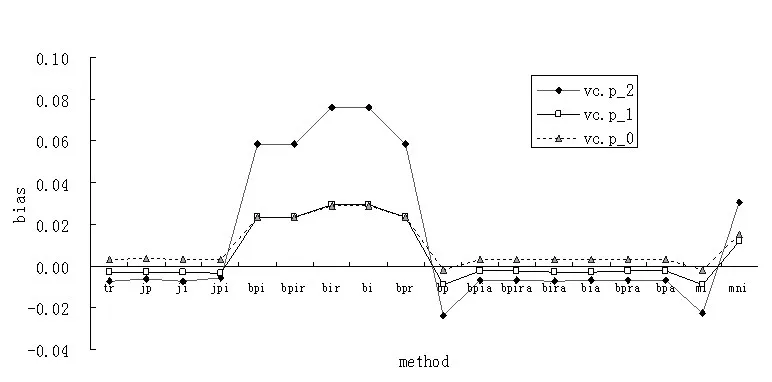
图2 三种偏态分布数据四种方法估计p的方差分量偏差

从图2可以看出，三种偏态分布数据四种方法估计p的方差分量偏差主要体现在未校正的Bootstrap方法和MCMC non-inf上，而Traditional方法、Jackknife方法（包括jack-p、jack-i和jpi）、校正的Bootstrap方法和MCMC inf方法偏差相对较小。特别地，当β=-2.0时，未校正的boot-pi、boot-pir、boot-ir、boot-i、boot-pr、boot-p 对应的绝对 偏 差 分 别 为 0.0587、0.0587、0.0760、0.0759、0.0587、0.0234，偏差相对较大，而校正的boot-pi、boot-pir、boot-ir、boot-i、boot-pr、boot-p 对应的绝对偏差分别为 0.0068、0.0068、0.0069、0.0070、0.0068、0.0068，偏 差 较 小 。 当β=-2、β=-1和β=0时，MCMC inf对应的绝对偏差值分别为0.0223、0.0087、0.0015，MCMC non-inf对应的绝对偏差值分别为0.0307、0.0118、0.0150，前者的偏差小于后者。从图2也可知，随着偏度由高偏趋于低偏过程中，偏差间距有逐渐缩小的趋势，且表现为先快后慢。当β=-2、β=-1和β=0时，各种估计方法的绝对偏差平均值分别为0.2464、0.0963、0.1738。对于三种不同偏态分布数据的vc.p，仅MCMC non-inf方法在个别方差分量估计出现不一致，但从总的趋势看，随着偏度值的减小，方差分量绝对偏差逐渐减小。

3.2 三种偏态分布数据估计的题目的方差分量偏差分析

根据表4中每种方法(或策略)估计的方差分量与参数的差值（bias），可以绘出三种不同偏态分布数据四种方法估计的题目的方差分量偏差图，如图3所示。

从图3可以看出，三种偏态分布数据四种方法估计i的方差分量偏差主要体现在MCMC non-inf上，而Traditional方法、Jackknife方法、Bootstrap方法和MCMC inf方法偏差相对较小。当 β=-2、β=-1和 β=0时，MCMC inf对应的绝对偏差值分别为0.0221、0.0080、0.0066，MCMC non-inf对应的绝对偏差值分别为0.2201、0.0660、0.0518，后者的绝对偏差是前者的9.96倍、8.25倍和7.84倍，可见MCMC inf的偏差是相当大，具有明显的“翘尾”。

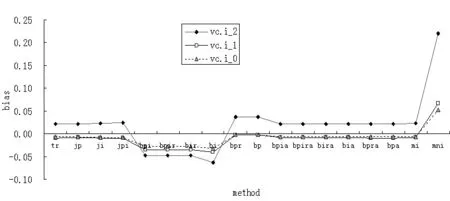
图3 三种偏态分布数据四种方法估计i的方差分量偏差

从图3也可知，当β=-2、β=-1和β=0时，各种估计方法的绝对偏差平均值分别为0.3093、0.1683、0.1512，随着偏度值的减小，方差分量绝对偏差有逐渐减小的趋势。对于三种不同偏态分布数据的vc.i，未出现“倒序”现象，方差分量绝对偏差有逐渐减小的趋势，也是先快后慢。

3.3 三种偏态分布数据估计的人与题目交互的方差分量偏差分析

根据表5中每种方法(或策略)估计的方差分量与参数的差值（bias），可以绘出三种不同偏态分布数据四种方法估计的人与题目交互的方差分量偏差图，如图4所示。

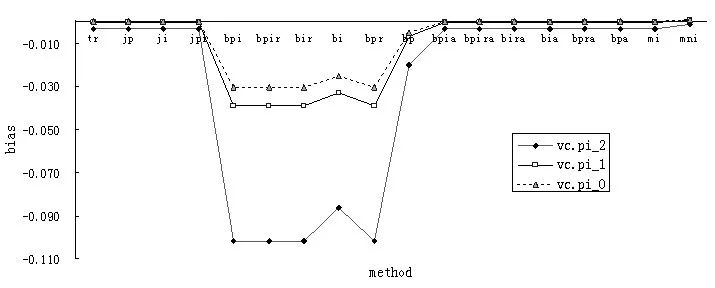
图4 三种偏态分布数据四种方法估计pi的方差分量偏差

从图4可以看出，三种偏态分布数据四种方法估计pi的方差分量偏差主要体现在未校正的Bootstrap方法上，而Traditional方法、Jackknife方法、校正的Bootstrap方法和MCMC方法偏差相对较小。当 β=-2.0时，未校正的boot-pi、boot-pir、boot-ir、boot-i、boot-pr、boot-p 对应的偏差分别为0.1020 、0.1019、0.1019、0.0862、0.1019、0.0199 ，偏差相对较大，而校正的boot-pi、boot-pir、boot-ir、boot-i、boot-pr、boot-p对应的偏差分别为0.0033、0.0033、0.0033、0.0033、0.0033、0.0033，偏差较小。当 β=-1.0 时，未校正的 boot-pi、boot-pir、boot-ir、boot-i、boot-pr、boot-p对应的偏 差 分 别 为 0.0390、0.0389、0.0389 、0.0329、0.0389、0.0069，偏差相对较大，而校正的boot-pi、boot-pir、boot-ir、boot-i、boot-pr、boot-p对应的偏差分别为0.0004、0.0003、0.0003、0.0004、0.0003、0.0004，偏差较小。 β=0 的情况类似。

从图4也可知，当β=-2、β=-1和β=0时，各种估计方法的绝对偏差平均值分别为0.5514、0.1988、0.1480，这表明偏度由大变小过程中，偏差减小的幅度前段速度较快，后段速度却较慢。对于三种不同偏态分布数据的vc.pi，从总的趋势看，随着偏度值的减小，方差分量绝对偏差逐渐减小。

4 结论

（1）利用广义双曲线分布性质可以有效模拟生成概化理论所需要的偏态分布数据。通过HyperbolicDist软件包的hyperbChangePars和rhyperb函数能够模拟生成偏态分布数据，根据估计偏态分布数据的方差分量及方差分量标准误，表明其具有对称性。利用GH分布性质模拟生成偏态分布数据，使得概化理论探讨偏态分布数据的方差分量估计，成为可能。

（2）广义双曲线分布模拟的偏态分布数据对概化理论各种方法估计方差分量有影响。分析三种模拟的偏态分布数据的vc.p、vc.i和vc.pi偏差，发现未校正的Bootstrap方法和MCMC non-inf方法偏差较大，而Traditional方法、Jackknife方法、校正的Bootstrap方法和MCMC inf方法偏差相对较小。从总的趋势看，随着偏度值减小，各种方法估计的方差分量偏差逐渐减小。

[1]Eberlein,E.,Hammerstein,E.A.Generalized Hyperbolic and Inverse Gaussian Distributions:Limiting Cases and Approximation of Process⁃es[M].University of Freiburg[Z].Nr.80,2003.

[2]Mena,R.H.,Walker,S.G.On the Stationary Version of the General⁃ized Hyperbolic ARCH Model.AISM,2007,59.

[3]任军峰.广义双曲线分布族下的金融市场风险度量[D].浙江工商大学硕士学位论文,2007.

[4]焦璨,张敏强,黄庆均,张文怡,黎光明.非正态分布测量数据对克伦巴赫信度α系数的影响[J].应用心理学,2008,14(3).

[5]Othman,A.R.Examining Task Sampling Variability in Science Perfor⁃mance Assessments[C].Unpublished Doctoral Dissertation,University of California,Santa Barbara,1995.

[6]Shavelson,R.J.,Webb,N.M.Generalizability Theory:a Primer[M].Newbury Park,CA:Sage,1991.

[7]Brennan,R.L.(Mis)Conceptions about Generalizability Theory[J].Ed⁃ucational Measurement:Issues and Practice,2000,19(1).

[8]Scott,D.The HyperbolicDist[EB/OL].http://www.r-project.org,2009.

[9]Tong,Y.,Brennan,R.L.Bootstrap Techniques for Estimating in Gener⁃alizability Theory(CASMA Research Report No 15).Iowa City,IA:Center for Advanced Studies in Measurement and Assessment,Uni⁃versity of Iowa[EB/OL].http://www.education.uiowa.edu/casma,2006.

[10]Tong,Y.,Brennan,R.L.Bootstrap Estimates of Standard Errors in Generalizability theory[J].Educational and Psychological Measure⁃ment,2007,67(5).