EM算法在卫星轨道计算中的应用＊

杜 琨，宋迎春，肖琴琴

（中南大学地球科学与信息物理学院，湖南 长沙410083）

0 引 言

利用GPS信号进行导航定位时，需要已知GPS卫星在空间的瞬时位置，卫星星历的精度将直接影响定位的精度和结果，因此，精确计算GPS卫星在空间的瞬时位置是精密定位的前提和基础［1－2]。随着现代测量、导航、气象等领域对卫星星历的精度和实时性的要求越来越高，对利用GPS广播星历和精密星历来准确计算卫星在空间的瞬时位置，变得越来越重要。目前，已有很多文献研究了利用精密星历文件计算任意时刻的卫星空间位置，且取得了很好的效果，然而这些研究工作都是基于数据完全，即星历文件数据准确、信息量较大无缺失数据时进行研究的［3－4]。在实际应用中，精密星历文件并不完全准确，由于卫星遮挡、卫星信号传播限制等多方面的原因，可能造成部分有用信息丢失，导致数据不完全。在这种情况下，如果仍采用常规的计算方法，则可能受到数据不完全的影响。对于信息量不足，通常只能降阶对其拟合或插值，这两种情况都会造成很大的误差，影响拟合或插值的效果。已有研究表明，对于15min历元间隔的精密星历而言，如果要精确至10－8，用8阶朗格朗日内插已足够保证精度，而切比雪夫多项式拟合至少需要12阶才能达到厘米级精度［3]。利用切比雪夫多项式拟合要达到厘米级精度，至少需要12组数据才能对其进行拟合。但由于精密星历是每15min一组，数据量相对较少，所以对于短弧段用切比雪夫多项式拟合不能满足要求。EM算法是一种常用的缺失数据处理方法，目前，已被广泛应用于测量领域。2010年，惠沈盈等把EM算法应用于数据缺失时的动态定位解算［5]，2011年，林东方等又把EM算法应用于数据缺失时的GPS高程拟合［6]，都取得了很好的效果。通过对EM算法的研究，对不完全数据添加与卫星轨道信息相关的“潜在数据”，能大大提高卫星拟合的精度。

1 常用的插值法和拟合法

精密星历文件是以离散的形式、按一定的时间间隔（通常为15min）给出卫星在空间的三维坐标、三维改正速度以及卫星钟改正数等信息。而在GPS事后数据处理中，经常要用到任意时刻的卫星坐标，因此需要对精密星历进行插值或者拟合以获得采样间隔更高的卫星轨道信息。利用精密星历文件计算卫星位置以及运动速度通常采用拉格朗日插值和切比雪夫拟合。

关于拉格朗日插值和切比雪夫拟合的原理已经在大量文献中有过说明，仅以切比雪夫多项式拟合为例。用n阶切比雪夫多项式来逼近时间段［t0，t0＋Δt]中的卫星星历时，先要将变量t∈［t0，t0＋Δt]变换为变量τ∈［－1，1]：

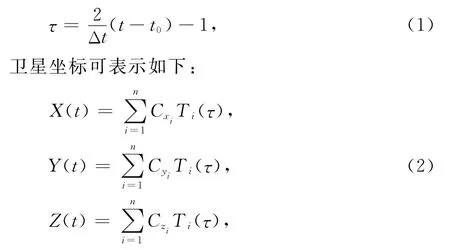
式中：n为多项式的阶数；Cxi，Cyi，Czi为切比雪夫多项式Ti的系数。切比雪夫多项式Ti的递推公式如下：

根据已知的卫星坐标，用最小二乘法拟合出多项式系数Cxi，Cyi，Czi后，就可以计算该时段任意时刻的卫星位置。

2 EM算法及其在卫星轨道计算中的应用

IGS精密星历文件经常因为计算失误、文件传播等原因导致部分数据失真或缺失。在数据缺失或数据量较少的情况下，无法采用高阶的插值法或拟合法。这时，只能降阶对其插值或拟合，从而导致计算精度降低。采用EM算法，添加与卫星轨道信息相关的“潜在数据”，可以有效解决这一问题，大大提高卫星拟合的精度。

2.1 EM算法的原理

EM算法是一种迭代算法。它的每一次迭代由两步组成：E步（求期望）和 M步（极大化）。一般，以P（θ／Y）表示θ的基于观测数据的后验分布密度，称为观测数据后验分布。以P（θ／Y，Z）表示添加数据（缺失数据）Z后得到的关于θ的后验分布密度函数，称为完全数据后验分布。P（Z／θ，Y）表示在给定θ和观测数据Y下潜在数据（缺失数据）Z的条件分布密度函数。我们的目的是计算观测后验分布P（θ／Y）的参数，EM 算法如下进行，记θi为第i＋1次迭代开始时后验参数的估计值，则第i＋1次迭代的两步为：

E步：将P（θ／Y，Z）或logP（θ／Y，Z）关于Z 的条件分布求期望，从而把Z积掉，即

M 步：将Q（θ／θi，Y）极大化，即找一个点θi＋1，使

如此形成了一次迭代θi→θi＋1，θi＋1∈M（θi），这里M（θi）是在整个参数空间Ω 内使得Q（θ／θi，Y）最大的θ的值所组成的集合。将上述E步和M步进行迭代直至‖θi＋1－θi‖或者‖（Q（θi＋1／θi，Y）－Ω（θ／Qi，Y）‖充分小时为止［5－7]。

2.2 EM算法在卫星轨道计算中的应用

以12阶切比雪夫多项式拟合为例。卫星的坐标可以表示为k阶切比雪夫多项式为

则误差方程为

式中：V为误差向量；C为拟合系数；T表示时间参数切比雪夫递推公式；l为观测向量（卫星坐标）。可以表示为

精密星历文件是以离散的形式、按一定的时间间隔（通常为15min）给出卫星在空间的三维坐标、三维改正速度以及卫星钟改正数等信息。在用多项式拟合其函数模型时，可以先对精密星历进行加密，而把加密时刻的数据当成是缺失数据，应用EM算法进行处理，从而提高拟合的精度。假设在上式中ln为缺失数据（加密时刻的卫星坐标数据），已知误差向量V服从高斯正态分布，利用EM算法建立似然函数方程P（θ／Y，Z），

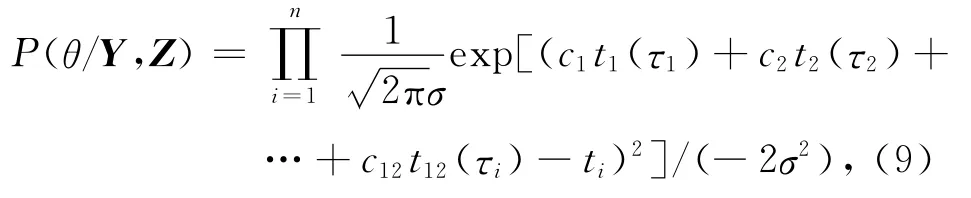
缺失数据ln的条件分布概率密度函数为

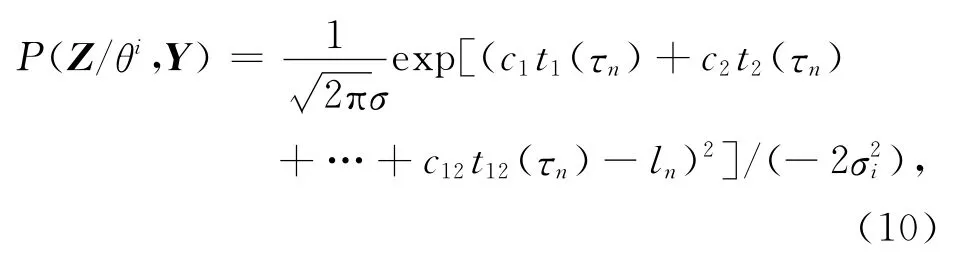
式中，θi为经过i次迭代后的参数值。

则得到EM算法的期望步：

EM 算法的极大化步，将Q（θ／θi，Y）极大化，积分后对各参数求偏导数，计算得到参数θi＋1，将θi＋1代入E步进行迭代，循环直至‖θi＋1θi‖或者‖Q（θi＋1／θi，Y）－Q（θi／θi，Y）‖充分小时为止。

3 算例分析

本例选取的数据是从IGS数据中心下载的2012年1月29日的精密星历。为了使拟合结果达到厘米级精度，这里选取1号卫星0时0分0秒每隔30min共12个历元的X方向的坐标值作为拟合节点的数据，而将15min间隔的数据作为已知数据进行对比。

分别采用12阶切比雪夫多项式拟合、同时假设拟合节点中第五个历元的数据为粗差或者丢失，在这种情况下降阶采用11阶切比雪夫多项式拟合以及采用EM算法处理后，再采用12阶切比雪夫多项式拟合，计算拟合弧段内每15min历元节点的结果如表1所示。

表1 拟合结果精度比较（单位：m）

在缺失数据下，降阶应用11阶拟合与采用EM算法处理后，再采用12阶切比雪夫拟合，其绝对误差曲线如图1所示。

图1 绝对误差曲线

从图1可以看出，由于4号和5号节点间的历元数据缺失，从而导致4号节点的拟合结果产生明显的振荡。而5号节点处于整个拟合弧段的中间，因此拟合结果较好。

4 结 论

由于精密星历是每15min一组，数据量相对较少，所以对于短弧段用切比雪夫多项式拟合不能满足要求。当不能采用12阶切比雪夫多项式拟合时，只能采用降阶拟合的方法，即采用11阶或者更低阶数的切比雪夫多项式来求取任意时刻的卫星空间坐标，此时，可能导致拟合精度无法满足要求，采用EM算法，通过对其添加与计算卫星位置有关的“潜在数据”，能有效解决这一问题，大大提高拟合的精度。由实验结果可以看出，在用切比雪夫多项式拟合内插拟合弧段内任意时刻的卫星位置时，拟合弧段两端节点的拟合效果较差，使用EM算法也出现了同样的问题。在数据缺失的情况下，与缺失数据相邻的节点拟合精度要相对较差。

［1]徐绍铨，张华海，杨志强，等.GPS测量原理及应用［M].武汉：武汉大学出版社，2007：11－86.

［2]李征航，张小红.卫星导航定位新技术及高精度数据处理方法［M].武汉：武汉大学出版社，2009：1－24.

［3]苟长龙.广播星历插值和精密星历外推方法研究［D].长沙：中南大学，2009：18－22.

［4]万亚豪，张书毕，侯东阳.GPS精密星历插值法与拟合法的精度比较［J].全球定位系统，2011，36（2）：1－4.

［5]惠沈盈.观测数据不完全的动态定位算法研究［D].长沙：中南大学，2010：12－14.

［6]林东方，宋迎春，肖琴琴.缺失数据下基于EM算法的GPS高程拟合［J].大地测量与地球动力学，2012，32（2）：1－4.

［7]杨基栋.EM算法理论及其应用［J].安庆师范学院学报·自然科学版，2009：1－5.