相对论框架下时间系统转换及SOFA软件的教学应用*
2013-07-18魏二虎李智强殷志祥
魏二虎,李智强,殷志祥,张 帅
(1.武汉大学测绘学院,湖北 武汉430079;2.武汉大学地球空间环境与大地测量教育部重点实验室,湖北 武汉430079)
0 现 状
在时间系统中,原时跟坐标时是两个不同的概念。原时是一个客观的物理量,可以用精确的计时工具直接测量,与坐标系的选择无关。也就是说,在任何参考系中,观测者的原时都是唯一确定的,如平太阳时、历书时、原子时等。而坐标时只是一个具有数学意义的“坐标量”,是在相对论框架下所导得的,与坐标系的选择密切相关[1]。
随着天文测地精度的提高以及相对论时空坐标理论的发展,对一些空间大地测量学中的基本概念的定义发生了重大变化。IAU2000通过了新的时空参考系和时间尺度,决议建议时空坐标理论必须在完整的后牛顿近似下来考虑。研究相对论框架下各种时间系统定义及转换,为空间大地测量学的研究提供明确的时间概念和理论基础。
将介绍相对论框架下时间系统的定义、用途以及如何利用IERS提供的SOFA天文库对不同时间系统进行转化。
1 相对论框架下的几种时间系统
1.1 地心坐标时(TCG)
地心坐标时(TCG)是原点位于地心的天球坐标系中所使用的第四维坐标——时间坐标,用于讨论绕地球运行的卫星等天体的运动规律、编制相应的星历。根据国际天文联合会(IAU)2000年B1.3决议中定义的地心天球参考系(GCRS)就是采用地心坐标时。它是把地球动力学时从大地水准面通过相对论转换到地心时的类时变量。
1.2 质心坐标时(TCB)
质心坐标时(TCB)是太阳系质心天球坐标系中的第四维坐标。它是用于计算行星绕日运动方程中的时间变量,也是编制行星历表时的独立变量。
1.3 地球时(TT)的定义与实现
地球动力学时(TDT)是建立在国际原子时TAI的基础上的,其秒长与国际原子时相等。1991年,第21届IAU大会决定将地球动力学时(TDT)改称为地球时(TT)。地球时(TT)和国际原子时(TAI)之间的关系式可以表示为:

根据原时τ与地心坐标时(TCG)的关系式[2],以及地球时(TT)与TCG的关系式,在忽略有关O(C-4)的项后,可得在一阶后牛顿精度下原时τ与地球时TT之间的关系为
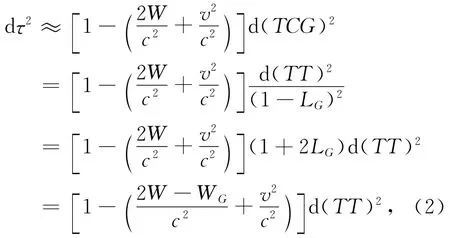
式中:WG为大地水准面上的重力位;W(t,x)在此可以理解为观测者在地球质心参考系中的位函数;V为观测者在非旋转地球质心参考系中的3维速度。对上式线性化并积分后,有

式中:τ0为TT=0时的原时钟读数(钟差);积分项为时钟的相对论效应改正,其中速度项为狭义相对论效应改正,引力为广义相对论效应[3]。
1.4 太阳系质心动力学时(TDB)的定义与实现
太阳系质心动力学时有时也被简称为质心动力学时。这是一种用以解算坐标原点位于太阳系质心的运动方程(如行星运动方程)并编制其星表时所用的时间系统。质心动力学时(TDB)和地球时的(TT)之间没有长期漂移只有周期项变化,即[4]

2 SOFA软件在时间系统转换中的应用
国际天文联合会(IAV)担负着讨论并制定国际上通用的天文标准的任务。常用的天文常数,有关地球自转轴运动的岁差,章动和极移等都是其制定的,并且被作为天文界中的标准。SOFA软件包就是IAU编写的有关天文基础标准的子程序库,旨在为天文计算提供权威有效的算法程序和常数数值。
目前最新版SOFA(截至2012年9月)包括了IAU在2006年公布的岁差模型,目前一共有186个子程序,主要用Fortran语言(F77)编写,每个子程序放在一个*.for的文件中。其主要内容包括两个方面:天文基础标准和基础向量操作。其中前者有131个子程序,可以进行天文历法计算、时间计算、星历表计算、岁差章动计算、恒星空间运动计算和主要星表系统的转换等;后者有55个子程序,主要功能是矢量和矩阵的各类操作。本文中坐标参考系之间转换采用的基础代码来源于该中心[5]。
在SOFA库中,提供20个子程序用于不同时间系统之间的转换。表1示出的是将实用到的一些子程序的说明,其余子程序如表1所示[6]。

表1 实现时间系统转换的一些程序的说明
2.1 TT与TCG之间的转换
TT是在标准的原子钟受到下列相对论效应影响的情况下来定义的,由式(3)可知其受到三部分的影响,分别为[7]:在大地水准面上的地球引力位而产生的广义相对论效应δt1;在地球上的太阳及其他行星的引力位而产生的广义相对论效应δt2;由于地球绕日公转的运动速度Ve而产生的狭义相对论效应δt3.
TCG用于讨论绕地球运行的卫星等天体的运动规律、编制相应的星历的一种时间系统。卫星离地面的高度可达数千至数万千米,由地球引力而产生的广义相对论效应必须根据每个卫星的具体情况分别加以考虑,而不能统一采用大地水准面上的数值δt1.所以在TCG中是不含δt1.由于在地球附近的卫星仍然会受到太阳和其他行星的引力位的作用,也会随着地球一起绕日公转,故TCG中仍含有δt2和δt3项。从上面的讨论可知TCG和TT的差异仅在于是否含δt1项。将广义相对论效应的公式代入后可导出TCG与TT间的关系式为

将 W0=62 636 856.0m2/s2,c=299 792 458 m/s代入后可求得LG=6.969 290 134×10-10,Δt=ti-t0,其中ti为任一时刻,t0为起始时刻1977年1月1日0h,用儒略日表示为JD=2 443 144.5,用简化的儒略日表示则为MJD=43 144.0.规定在起始时刻TCG=TT.式(7)可写为

在SOFA函数库中,可由子程序IAU_TTTCG以及子程序IAU_TCGTT实现TT与TCG之间的转换,其具体调用语句为CALL IAU_TTTCG(TT1,TT2,TCG1,TCG2,J);CALL IAU_TCGTT(TCG1,TCG2,TT1,TT2,J)
语句 CALL IAU_TTTCG(TT1,TT2,TCG1,TCG2,J)中,TT1、TT2为双精度实数输入量,是TT两部分表示,可以有以下4种表示方法.

表2 TT1与TT2的表示方法
输出量为TCG1、TCG2、J,TCG1、TCG2为双精度实数,格式与输入的TT1、TT2相对应;J为整型,其值恒为0,表示转换无异常。
TCG转换为TT类似上述过程。
在研究过程中,为了分析TT与TCG转换过程中SOFA软件的自恰性,同时对上述过程进行了调用。本示例采用武汉2012年9月25日16∶00(UTC)作为起始数据,利用SOFA提供的IAU_CAL2JD、IAU_UTCTAI、IAU_TAITT(程序具体说明参见文献[8])计算TT和TCG,并利用所求结果做差,得到较差项,具体计算结果如表3所示。
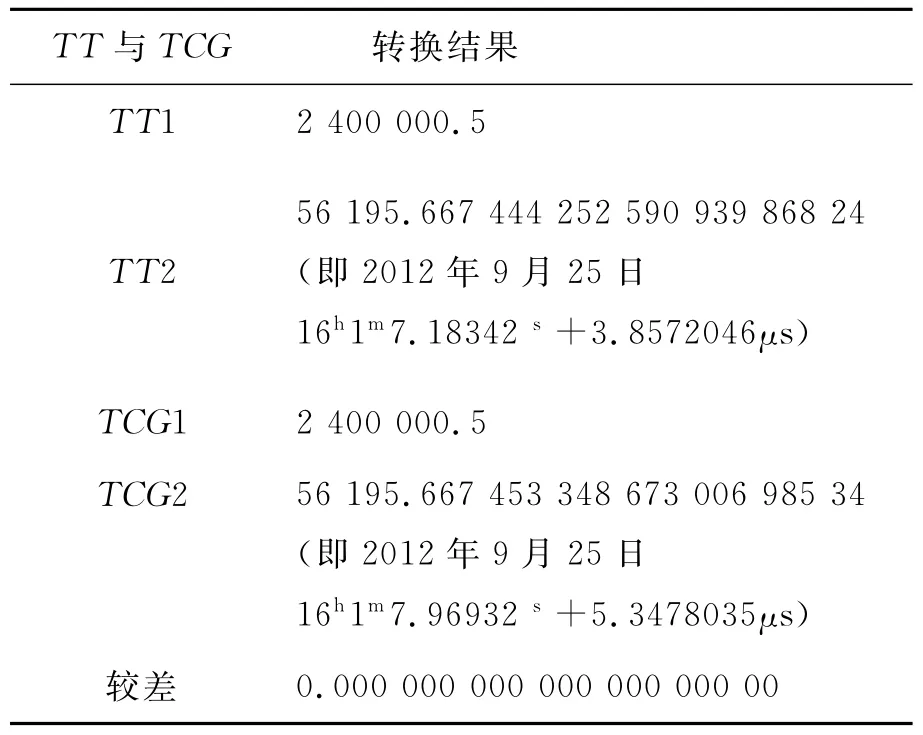
表3 TT与TCG间转换示例结果
2.2 TT与TDB之间的转换
国际原子时(TAI)是地球坐标时,更严格地讲是大地水准面处的时间尺度。考虑到相对论效应对时间尺度的影响,20世纪7年代国际天文学会(IAU)定义了地球力学时TDT和质心力学时TDB.随着天文观测精度的提高以及由于TCB和TDB在实际应用中存在的具体问题,国际天文学会在2006年又重新定义了TDB,明确定义了TDB与TCB之间的线性变换关系,同时为了不让TT与TDB出现很大的差异,规定这两种时间系统不存在长期变化项而只允许存在周期项。也就是说TT和TDB之间是不允许存在系统性的时间尺度比的,而只允许在不同时刻TDT(TT)与TDB间存在微小的周期性的差异,但在一个周期内这两种时间系统的“平均钟速”是相同的。
传统上一般采用解析法将TT转换到TDB:

文献[4]指出,Irwin和Fukushima利用JPL的现代DE405数值历表,采用数值积分方法计算了TT到TDB的转换结果,与上述解析法结果比较,发现解析法结果存在明显系统误差,最大50ns左右。
对于TT与TDB之间的关系,在文献[7]中采用将TT→TCG,然后将TCG转换到TCB,最后把长期项去掉,只留下周期项。得到TT与TDB间关系式如下:

由于TDB中已按IAU的规定去掉了长期项,而光速c为常数,因而TT与TDB间的时间尺度比LB只能隐含到长度中去。也就是说在TT和TDB中的单位长度是不一样的。两者之间有下列关系式为

在SOFA程序库中,采用了Fairhead和Bretagnon给出的解析表达式计算TDB-TT 的值,调用语句:DTR=IAU_DTDB(DATE1,DATE2,UT,ELONG,U,V);ALL IAU_TTTDB(TT1,TT2,DTR,TDB1,TDB2,J);CALL IAU_TDBTT(TDB1,TDB2,DTR,TT1,TT2J).
函数IAU_DTDB(DATE1,DATE2,UT,ELONG,U,V),返回值为TDB与TT 之差,为双精度实数。在参数部分,DATE1/DATE2为儒略时两部分表示,具体表示方法与2.1类似;UT为世界时,其中包含UT1和当前时间在当天的小数表示;ELONG为东经的弧度表示;U 为距旋转轴距离,单位km;V 为距北赤道平面距离,单位km.
在子过程IAU_TTTDB中,前两个参数TT1、TT2为TT的儒略时两部分表示,DTR为前面调用函数返回值,TDB1、TDB2为返回值,结构跟TT类似。
子过程IAU_TDBTT为IAU_TTTDB逆过程,参数结构与IAU_TTTDB类似。
同2.1,为了研究转换过程中的软件自恰性,对TT与TDB转换过程也进行了验证。在此例中,需要说明的有2点:
1)由前述分析可知,在TT与TDB相互转换过程中需要调用函数IAU_DTDB,且函数IAU_DTDB的参数中含有观测者的子午面直角坐标,即ELONG(东经的经纬度弧度表示),U(子午面直角坐标中X),V(子午面直角坐标Y),具体计算参见文献[9]中4.2节。在此例中分别对武汉、伦敦以及纽约进行了计算,由计算结果可得两地的TT一致,但TDB出现了差异,究其原因可参见公式(9),由于TT1、TT2与表3相同,同时TDB1是简化儒略日表示,为避免重复,在本例中对其结果没有予以表示,TDB2的具体数值如表4所示。数据表明由测站位置引起的TDB差异可达到1.26 μs,在实际应用过程中需要注意。

表4 武汉、伦敦及纽约同一时刻TDB2值
2)由计算结果可以发现,较差项始终为零,表明TT与TDB之间的转换自恰性非常好。
2.3 TT和TCB间的转换
2006年IAU做出决议,定义TDB和TCB之间存在如下的线性变换关系:

式中:JDTCB为TCB 儒略日;T0=2 443 144.500 372 5;LB=1.550 519 768×10-8和TDB0=-6.55×10-5s为定义常数。由2.1可知,TCG和TT间也存在一个线性变换关系,对式(6)与式(10)进行运算,可得:

由于SOFA程序库中没有直接实现TT到TCB转换的程序,但可以利用TDB作为中间变量,进而实现所需要的转换,调用语句如下:CALL IAU_TTTDB(TT1,TT2,DTR,TDB1,TDB2,J);CALL IAU _TDBTCB(TDB1,TDB2,TCB1,TCB2,J;CALL IAU_TCBTDB(TCB1,TCB2,TDB1,TDB2,J);CALL IAU_TDBTT(TDB1,TDB2,DTR,TT1,TT2,J).
参数部分与前面类似,格式同前。
分别采用了武汉、伦敦以及纽约三地2012年9月25日16∶00(UTC)进行了实例验证,表5示出的是TCB2的值。

表5 武汉、伦敦及纽约同一时刻TCB2值
与2.2节对应,有两点需要说明:
1)由结果可以看出武汉、伦敦及纽约三地TCB时间也存在差别。
2)示例结果表明对转换过程做逆转换之后得到的结果与初值做较差,其值为零,TT与TCG之间转换的自恰性非常好。
3 结 论
相对论框架下时间系统的定义和转换是空间大地测量里面绕不开的一个问题,面对日益发展的空间大地测量学,如何更精准的定义时间系统以及完成它们之间的转换是一个非常有意义的问题。
系统阐述了相对论框架下一些时间系统的实现及其之间的转换,给出了相应的公式,并利用SOFA程序库给出的子程序对不同时间系统做了相应的转换,其结果在实际操作中得到了验证。
现阶段,随着高精度天文观测的发展,在TT与TDB转换中,以由DE405数值积分得到的时间坐标转换结果比传统的解析法结果更为可靠[10]。另外,不同版本的解析表达式包含不同数量的周期项,这会导致解的非唯一性。解析方法的优点是应用方便,在脉冲星计时观测精度低于100ns的情况下,可以采用解析算法。但随着脉冲星计时观测精度的提高,如目前Parkes 64m射电望远镜对毫秒脉冲星PSR J0437-4715的计时观测精度达到56ns,这要求时间坐标相对论转换计算能达到0.1as精度。因为一般情况下,理论模型误差应该比观测误差小1~2个量级。显然,传统的解析算法不能满足高精度观测的需求[11]。这将有待后续研究。
[1]张捍卫,王志军,杜 兰.完整后牛顿近似下原时与坐标时的转换[J].测绘学院学报,2004,20(2):79-81.
[2]CAPITAINE N,GAMIS D,MCCARTHY D D,et al.IERS technical note(29)[C]//Proceedings of the IERS Workshop or the Implementation of the NEW IAU Resolusion,Paris France,18-19April 2002.
[3]张捍卫,马国强,杜 兰.广义相对论框架中有关时间的定义与应用[J].测绘学院学报,2004,21(3):160-162.
[4]IRWIN A W,FUKUSHIMA T .A numberical time ephemeris of the earth[J].Astron Astrophys,1999(348):642-652.
[5]魏二虎,畅 柳,杨洪州.基于SOFA的ITRS与ICRS相互转换方法研究[J].测绘信息与工程,2012,37(1):31-33.
[6]IERS.IAU information buller[EB/OL].[2004-08-01].http://hpiers.obspm.fr/eoppc/bul/bulb/explanatory.html.
[7]杨挺高,高玉平.脉冲星时间尺度及其TOA预报初步分析[J].时间频率学报,2012,35(1):16-23.
[8]International Astronomical Union.SOFA Time Scale and Calendar Tools[EB/OL].[2012-12-24].http://www.iausofa.org/2012_0301_C/sofa/so fa_ts_c.pdf.
[9]孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社,2005.
[10]黄天依,许邦信.相对论框架里的时间尺度[J].天文学进展,1989,7(1):43-51.
[11]WEI,Erhu,YAN Wei,JIN Shuanggen,et al.Improvement of Earth orientation parameter estimates with Chang′E-1⊿ VLBI observations[J/OL].Geodynamics,2013(64):1-18[2013-04-20].http://www.sciencedirect/science/article/pii/so 264370713000604.
