GH3044的高温低周疲劳性能研究

张仕朝， 于慧臣， 李 影

（1.北京航空材料研究院航空材料检测研究中心，北京100095;2.航空材料检测与评价北京市重点实验室，北京100095;3.先进高温结构材料国防科技重点实验室，北京 100095）

GH3044合金为固溶强化镍基抗氧化合金，在900℃以下具有较高的塑性和中等的热强性，并具有优良的抗氧化性能，适宜制造900℃以下长期工作的航空发动机主燃烧室和加力燃烧室零部件［1］。航空发动机中的热端部件，在实际服役条件下，由于长期承受高温及复杂交变载荷的作用，经常产生高应力（应变）水平的低周疲劳损伤现象。因此，高温应变疲劳所造成的损伤成为影响此类构件使用寿命的一个不容忽视的因素。本工作对GH3044合金在600℃下应变控制模式的低周疲劳性能进行了分析与测试，研究了循环应力-应变响应行为、应变-寿命关系等，探明了该合金在应变控制下的疲劳变形和损伤的一般规律，并采用多种模型对合金的疲劳寿命进行了预测，可为该合金的部件设计、定寿和延寿工作提供参考依据。

1 试验材料

试验用材料为GH3044棒材，材料的密度为8.89×103kg/m3。合金采用电弧炉加真空自耗重溶工艺熔炼，轧制成φ18mm×1000mm的棒材，经固溶（1140℃，保温1h，空冷）热处理后，按图1加工成低周疲劳试样进行试验。合金的化学成分见表1。

表1 GH3044合金的化学成分（质量分数/%）Table 1 Chemical composition of superalloy GH3044（mass fraction/%）

2 试验方法

低周疲劳试验是在岛津EHF-EA10电液伺服疲劳试验机上进行，试验采用轴向全应变控制，引伸计的标距为12mm，引伸计通过石英刀口与试样表面接触测量标距内的应变。加载波形为总角波，应变比（最小应变与最大应变之比）为-1，试验温度为600℃，通过炉内电阻丝辐射加热试样，由分布于标距附近的热电偶控制温度的波动，温度波动控制在±2℃。实验数据的采集由计算机完成，各个试验均进行至试样断裂。试验方法参照 GB/T 15248—2008《金属材料轴向等幅低循环试验方法》［2］中的规定执行。断裂后的试样经超声波清洗后，用扫描电镜JSM 5600LV观察了断口形貌。

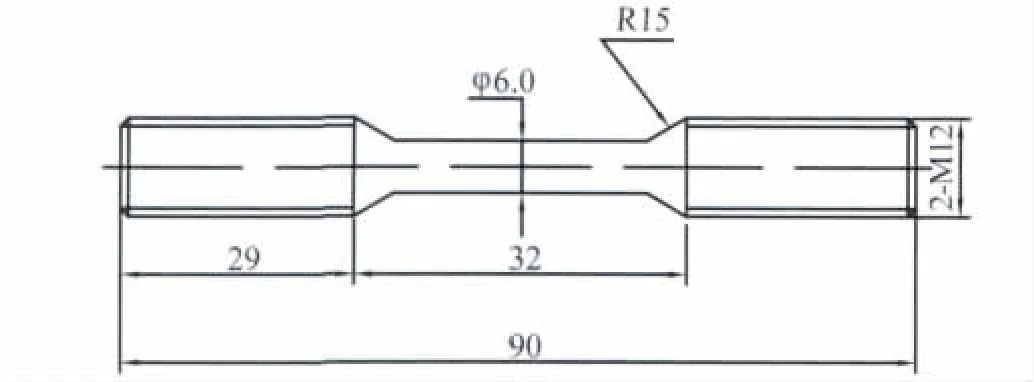
图1 低周疲劳试样Fig.1 Low cycle fatigue test specimen

3 试验结果与分析

3.1 循环应力应变行为

材料的循环应力-应变性能反映了材料在低周疲劳下的真实应力-应变特性。循环应力-应变关系可以用应力幅与塑性应变幅来表达［3］，即公式（1）:

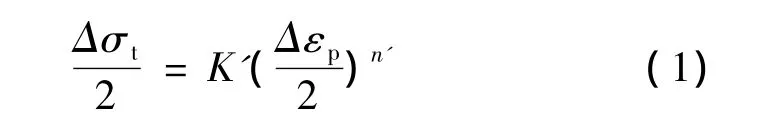
其中Δσt/2为循环应力幅，Δεp/2为循环塑性应变幅，n'为循环硬化指数，K'为循环强度系数。图2所示为GH3044合金在600℃下的循环应力-应变关系曲线，图中数据点均由半寿命（Nf/2）时的循环滞后回线求得。根据公式（1）采用双对数坐标对数据进行线性回归分析，即可得到n'和K'的值，见表2。图中实线是通过对试验数据拟合得到的近似曲线。

图2 GH3044合金600℃下的循环应力-应变曲线Fig.2 Cyclic stress-strain curve of GH3044 alloy at 600℃

表2 GH3044合金的低周疲劳参数Table 2 Low cycle fatigue parameters for GH3044 superalloy at 600℃

3.2 循环应力响应行为

在低周疲劳性能测试中，对每一给定的总应变幅都记录下应力值随循环周次的变化情况。应力值随循环周次的变化（即材料的循环应力响应曲线）宏观反映了合金在不同温度下及其他试验条件下的应变硬化/软化行为，是材料微观组织变化的宏观体现。图3为GH3044合金600℃下的循环应力响应曲线。由图3可见，在不同的外加总应变幅下，GH3044合金600℃时均表现为循环硬化现象，这由于在疲劳循环变形过程中，位错间以及位错与析出相间的交互作用均会对位错运动产生强烈的阻碍作用，使位错塞积，这就必须增大外加载荷才能维持应变恒定，从而导致循环应力增加即发生循环应变硬化［4］;图中还出现应力突然下降的阶段，这种突然下降是由于经过多次的循环变形，材料出现疲劳损伤而进入裂纹失稳扩展的阶段。

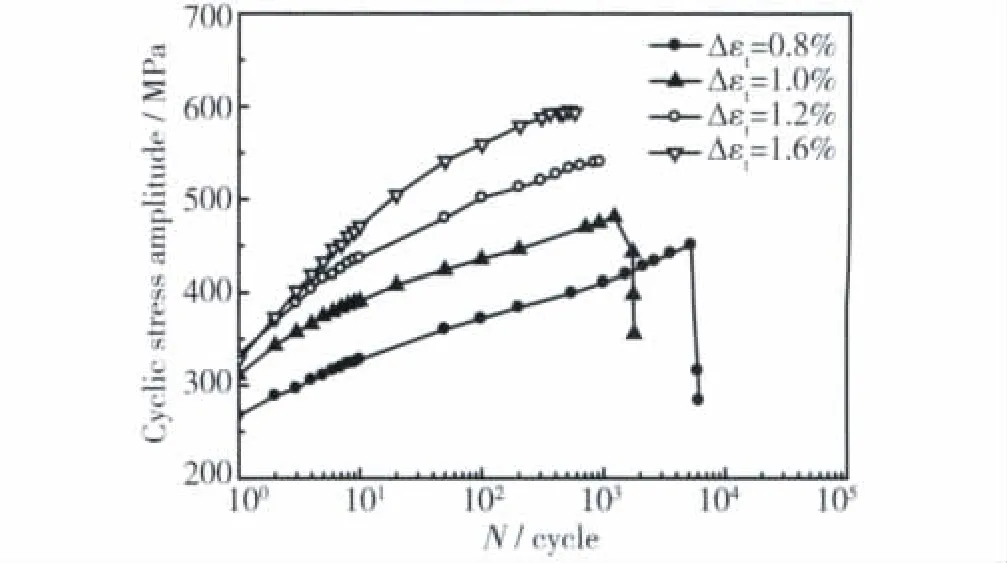
图3 GH3044合金600℃的循环应力响应曲线Fig.3 Cyclic stress response curves at 600℃

3.3 LCF 寿命预测

3.3.1 Manson-Coffin方程

目前国内材料数据手册处理低周疲劳时沿用Manson-Coffin方程。对于总应变控制的低周疲劳试验，总应变幅由塑性应变幅和弹性应变幅两部分组成［5］，即有:

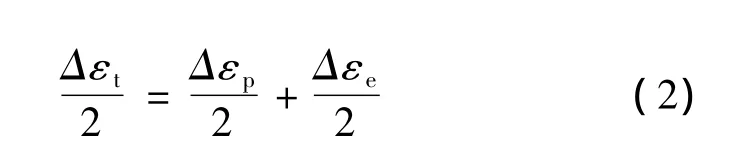
式中 Δεe/2，Δεp/2，Δεt/2分别为弹性应变幅、塑性应变幅和总应变幅。对于不存在稳定迟滞回线的材料，塑性应变幅和弹性应变幅通常由半寿命时的应力-应变迟滞回线求得。而且二者与疲劳寿命Nf分别有如下关系:

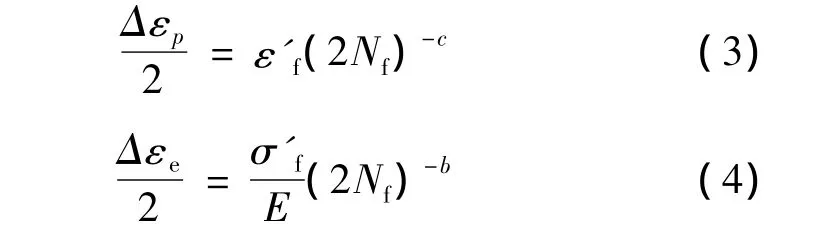
式中σ'f为疲劳强度系数，ε'f为疲劳延性系数，2Nf为断裂时加载反向数，b为疲劳强度指数，c为疲劳延性指数，E为弹性模量MPa，为了更实际的反映低周疲劳特性，实际运算中弹性模量取循环条件下的动态弹性模量［6］。总应变幅与材料的低周疲劳寿命间的关系可表示为:

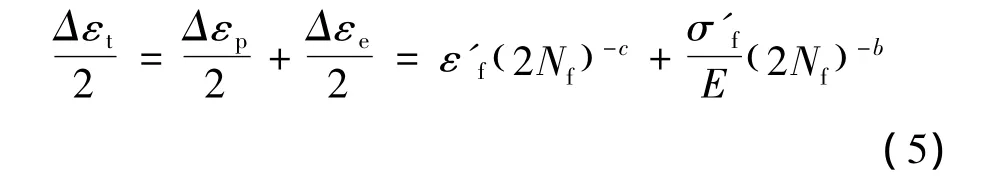
Manson-Coffin方程的寿命预测结果如图4所示。由图4可见，所有数据点基本落在2倍的分散带以内。

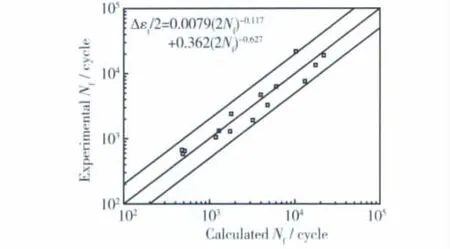
图4 Manson-Coffin方程预测结果Fig.4 Life prediction result predicted by Manson-Coffin equation

3.3.2 数幂函数方程

傅惠民［7］在对大量的ε-N曲线试验数据进行分析和研究后提出了三参数幂函数方程:

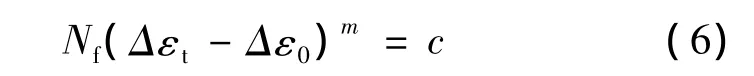
式中Δε0，m，c均为待定常数。

目前MMPDS-04［8］在处理低周应变疲劳试验数据时也采用三参数幂函数公式。三参数幂函数方程的寿命预测结果如图5所示。由图5可见，所有数据点基本落在2倍的分散带以内。

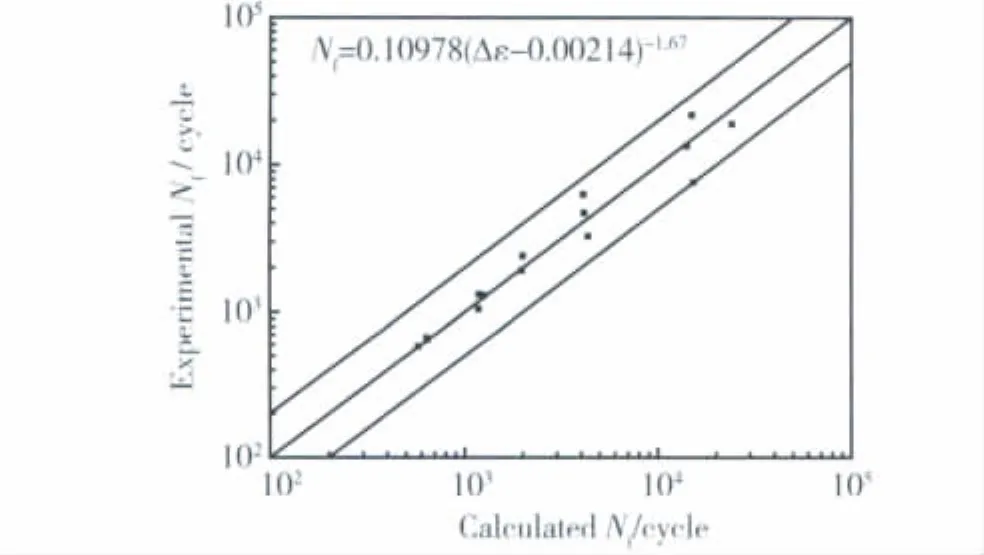
图5 三参数幂函数预测结果Fig.5 Life prediction result predicted by three-parameter power function

3.3.3 拉伸滞后能模型

拉伸滞后能模型由Ostergren［9］提出，该方法认为低周疲劳损伤由试样吸收的拉伸滞后能或应变能来控制的。可近似将滞后能ΔW表征为非弹性应变Δεin和峰值拉伸应力σmax的乘积，而滞后能与疲劳寿命之间遵循幂指数关系:

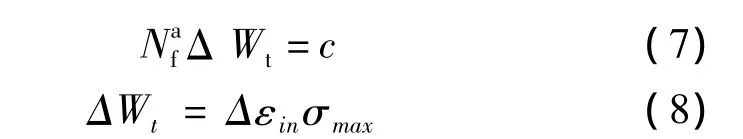
Δεin为非弹性应变，纯疲劳时用塑性应变Δεp代替。

拉伸滞后能寿命模型方程的寿命预测结果如图6所示。由6图可见，所有数据点落在1.66倍的分散带以内。

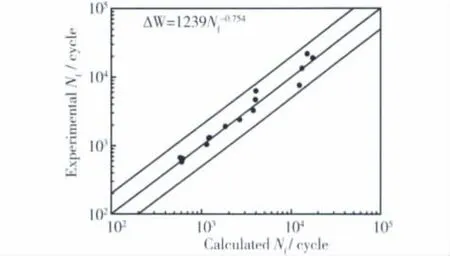
图6 拉伸滞后能模型预测结果Fig.6 Life prediction result predicted by Ostergren model

3.4 寿命预测能力的定量评定

工程上常用一种寿命预测模型对试验数据的相关能力来评定该预测模型的预测能力。试验数据的相关能力可用分散带（表明预测寿命和观测寿命的偏离程度）和标准差（表明数据组在平均值附近的程度）2个统计量来表示。标准差越小，表示模型的寿命预测能力越好。标准差s通常定义如下:

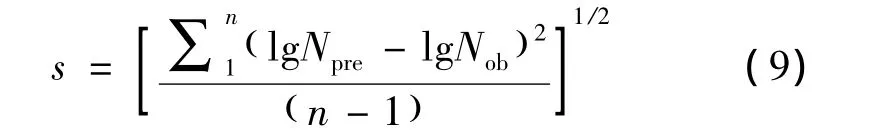
式（9）中，Npre代表预测寿命，Nob代表实测寿命，n为数据点数。相应的分析结果见表3。由表3和图4～图6可以看出，拉伸滞后能模型无论从分散带还是标准差方面比较，都比Manson-Coffin方程和三参数幂函数方程对GH3044合金600℃下的LCF寿命有更好的预测精度。

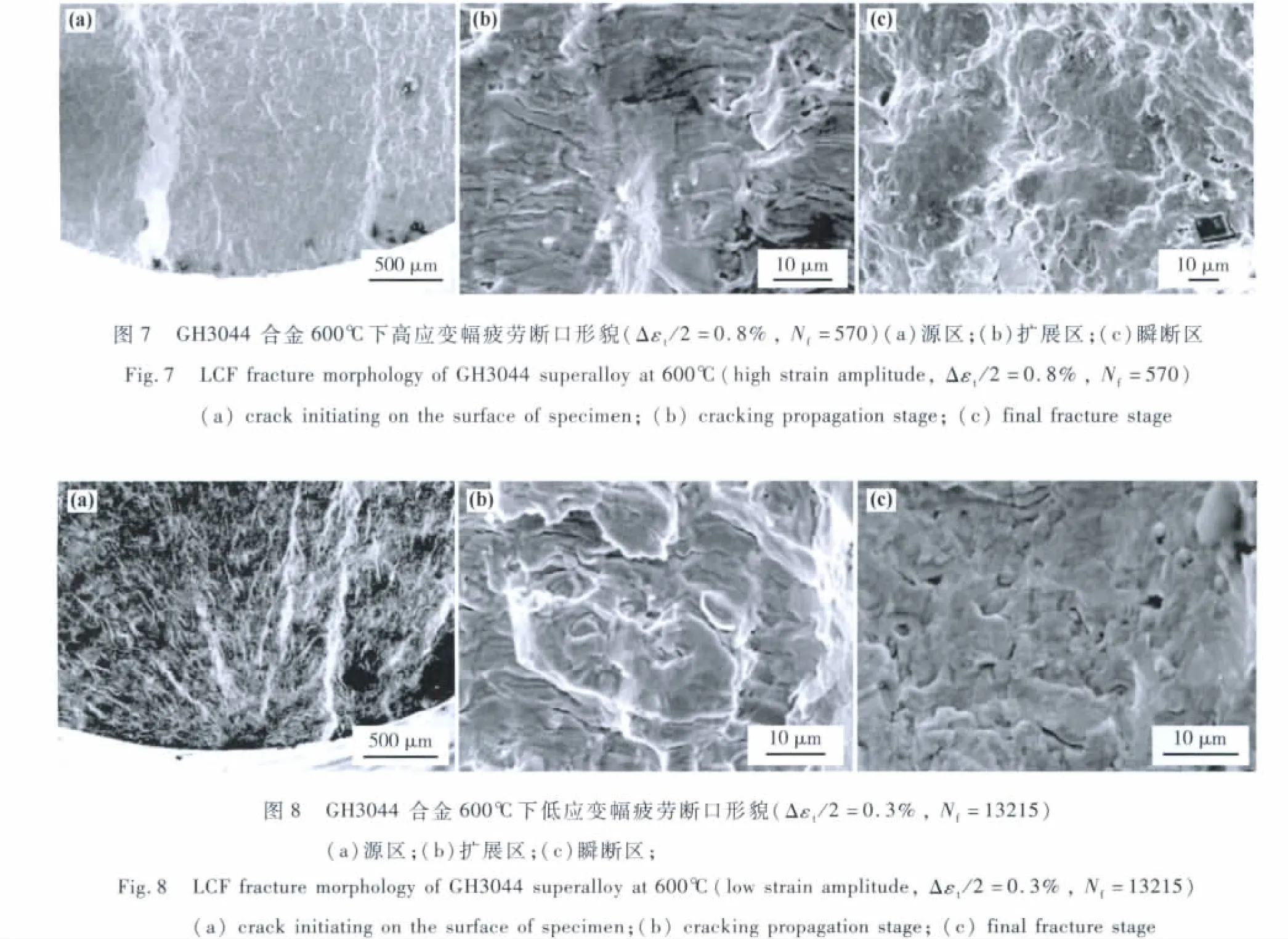
3.5 低周疲劳断口形貌

对GH3044合600℃下的低周疲劳断口形貌进行了观察，当应变幅较大时，断口疲劳区较小，应变幅较小时，断口疲劳区所占的比例较大，均可见疲劳断裂的3个区域，即疲劳源区、扩展区和瞬断区。图7和图8分别为 GH3044合金600℃下高应变幅（Δεt/2=0.8%，Nf=570）和低应变幅（Δεt/2=0.3%，Nf=13215）的疲劳断口形貌特征。由图可见，不同应变幅下疲劳裂纹均沿着试样表面起裂，但高应变幅下，疲劳裂纹沿试样表面呈多点起源（见图7a），且源区附近可见明显的放射棱线形貌;而低应变幅下，疲劳断口起源于试样的表面，且为点源（见图8a），不同应变幅下扩展区可见明显的疲劳条带及二次裂纹的特征（见图7b、见图8b），瞬断区呈现韧窝断裂特征，但韧窝较浅，有擦伤痕迹（见图7c、见图 8c）。

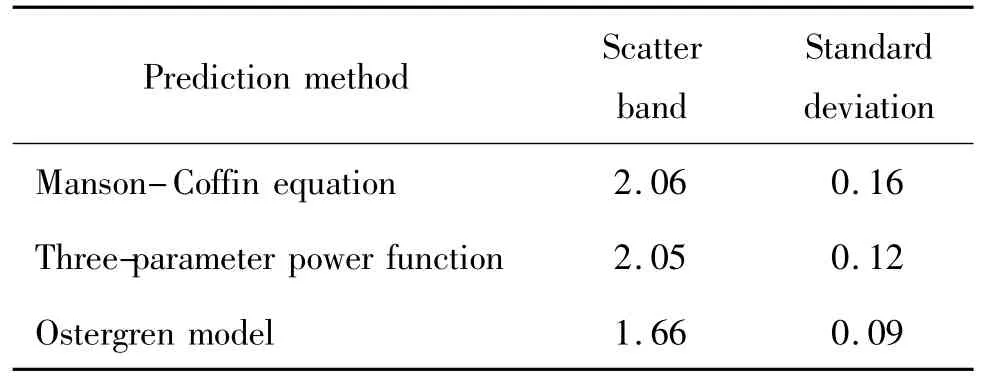
表3 寿命预测能力评估结果Table 3 Evaluation of life prediction

4 结论

（1）GH3044合金在600℃时在不同应变幅下均呈现循环硬化的现象;

（2）Manson-Coffin方程、三参数幂函数方程和拉伸滞后能模型（Ostergren）对GH3044合金600℃时寿命预测精度在基本在±2倍分散带以内，但拉伸滞后能模型的寿命预测结果无论从标准差，还是分散带等方面比较都比Manson-Coffin方程、三参数幂函数公式的寿命预测精度好;

（3）疲劳裂纹均从试样表面处起源，但高应变幅下呈现多源特征，低应变幅下呈现单源特征。

［1］《中国航空材料手册》编辑委员会.中国航空材料手册（第2卷）:变形高温合金铸造高温合金［M］.北京:中国标准出版社，2002:203.

（China aeronautical materials handbook Edit Committee.China aeronautical materials handbook（Vol.2）:Wrought superalloys Cast superalloys［M］.Beijing:China Standard Press，2002:203）

［2］GB/T15248-2008金属材料轴向等幅低循环疲劳试验方法［S］.北京:中国标准出版社，2008.

［3］ Suresh.S.Fatigue of Material［M］.Cambridge:Cambridge University Press.1998.

［4］王拴柱.金属疲劳［M］.福州:福建科学技术出版社，1985，73.

［5］ASTM E606 Standard Practice for Strain-controlled Fatigue Testing［S］.2005.

［6］张国栋，苏彬，王泓，等.弹性模量对低周疲劳性能参数的影响［J］.航空动力学报，2005，20（5）:768-771.

（ZhANG Guo-dong，Su Bin，Wang Hong，et al.Effect of elastic modulus on parameter of low cycle fatigue performance［J］.Journal of Aerospace Power，2005，20（5）:768-771）

［7］傅惠民.ε-N曲线三参数幂函数公式［J］.航空学报，1993，14（3）:173-176.

（Fu H M.A formula of three-parameter power function for ε – Ν curves［J］.Acta Aeronautica et Astronautica Sinica，1993，14（3）:173-176.（in Chinese））

［8］ Federal Aviation Administration（FAA）.MMPDS-04（The Metallic Materials Properties Development And Standardization Handbook）［M］，2009.

［9］OSTERGREN W J.A damage function and associated failure equation for predicting hold time and frequency effects in elevated temperature low cycle fatigue［J］.Journal of Testing and Evaluation，1976，4（5）:327-339.