基于XRD的径向分布函数法研究碳纤维制备过程中的结构演变

林 雪， 王成国， 于美杰， 徐 勇， 林治涛， 张 姗

（1.山东大学材料液固结构演变与加工教育部重点实验室，济南250061;2.山东大学山东省碳纤维工程技术研究中心，济南250061;3.山东建筑大学材料科学与工程学院，济南 250101）

双体分布函数表示为

式中结构函数

聚丙烯腈（PAN）基碳纤维及其复合材料具有高比强度、高比模量、耐热、耐化学腐蚀等优异性能，在航空航天、石油化工、交通运输、体育休闲以及国防军事等领域应用广泛［1，2］。研究表明，目前在航空航天等高科技领域中大量应用的碳纤维多为通用级的小丝束、高强度T300型碳纤维，其石墨化程度较低，微观结构以非晶态和纳米晶为主。大量文献中通常采用X射线衍射（XRD）、透射电子显微镜（TEM）、扫描电子显微镜（SEM）等传统的研究方法对碳纤维的结构进行研究［3～7］，但这些方法无法对非晶态结构进行深入分析，因此不能有效诠释碳纤维在制备过程中的结构演变。目前对液态非晶和非晶合金的研究主要是借助统计物理学的径向分布函数法（Radial distribution function，RDF），国内外一些学者利用RDF对多孔碳、富勒烯C60等不同类型的碳材料结构进行了研究，取得了许多创新性研究成果［8～13］。本工作首次采用该方法研究了碳纤维在制备过程中的结构演变，结果表明，该方法不但能够揭示碳纤维中乱层石墨结构的本质，而且还能够从原子级别解析在整个碳纤维制备过程中纤维结构从有序向无序，再从无序向有序的转变历程，这将为制备高性能碳纤维发挥重要指导作用。

本工作首先利用XRD对PAN原丝、预氧丝和不同温度的碳化纤维进行了全谱散射实验，并对XRD数据进行了校正和截尾效应处理，在此基础上通过傅立叶变换获得了多个RDF函数，利用对RDF曲线的详细分析发现了一些新的结构信息。

1 实验部分

1.1 试样制备

（1）原丝（编号:PF）:实验室自制湿纺PAN原丝，该原丝的基本性能指标列于表1。

（2）预氧丝（编号:OF）:即预氧化纤维。OF由PAN原丝在200～270℃的预氧化处理后获得。预氧化过程中纤维施加适当牵伸，预氧化气氛为空气。

（3）碳化纤维（编号:CF500～CF1250）:采用不同的碳化温度在高纯氮气保护下对预氧丝进行碳化处理，碳化过程中纤维施加适当牵伸。样品的最高碳化温度分别设为500℃，700℃，800℃，900℃，1100℃和 1250℃，以上样品分别编号为:CF500，CF700，CF800，CF900，CF1100，CF1250。

表1 原丝PF的基本性能Table 1 Main properties of precursor fiber PF

1.2 分析测试

利用阿基米德法分别对 PF，OF和 CF500～CF1250各试样的密度进行测试。

将纤维剪碎，试样用量约为2 mg。利用德国Vario EL III型元素分析仪对 PF，OF和 CF500～CF1250各纤维的C，N，H，O元素含量进行分析。

将PF，OF和CF500～CF1250各纤维分别进行研磨至粉末状，以进行XRD实验。

XRD实验在Bruker D8 Advance X射线衍射仪上进行，采用Cu靶Kα辐射源，X射线波长为λ=0.15418nm，加速电压和电流分别为40 kV和40 mA。扫描范围2θ为 5°～130°，扫描步长为0.02°，步进:0.5s/step（扫描速度约1°/min），收集衍射强度数据。实验过程中保证计数强度都大于104。

1.3 数据处理

实验测量的X衍射强度包含空气散射、非相干散射和多重散射以及偏振因数和吸收因数的影响，必须扣除或校正这些影响因素，然后进行衍射强度的坐标转换和标准化处理，才能进行RDF的计算［14］。

数据处理流程如图1所示:

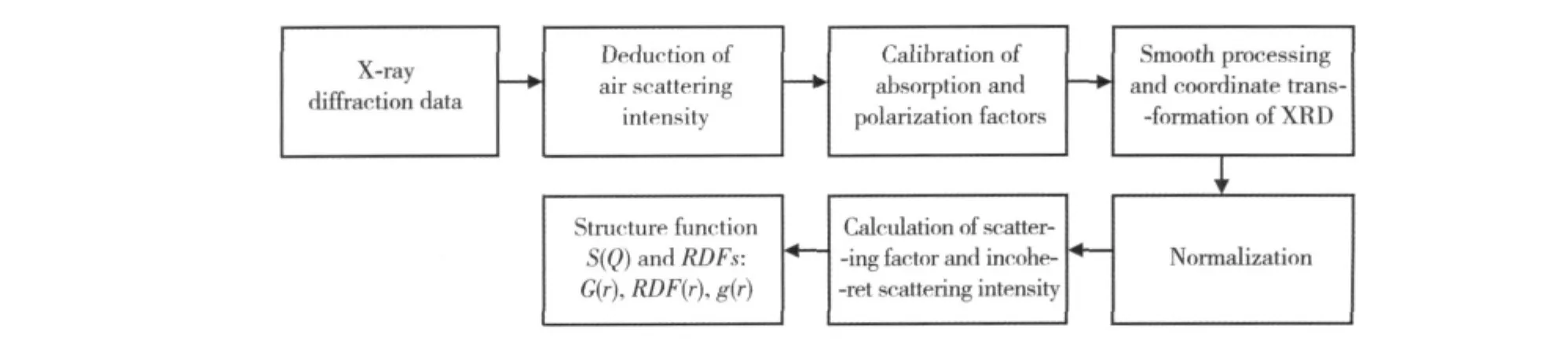
图1 原子径向分布函数数据处理流程图Fig.1 Data processing flow chart of RDF

图1中所列出的径向分布函数满足以下关系［14］:

原子径向分布函数可表示为

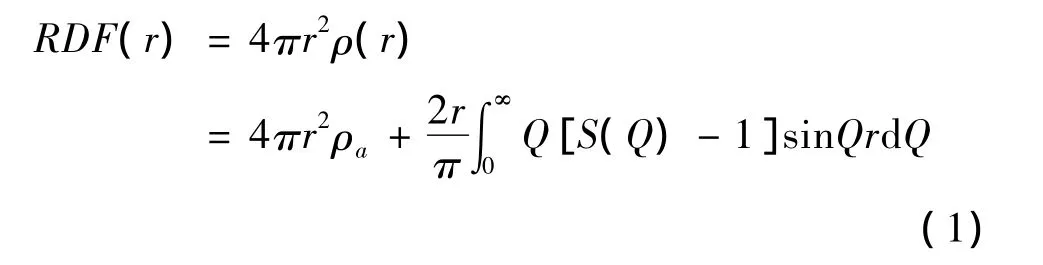
约化径向分布函数表示为

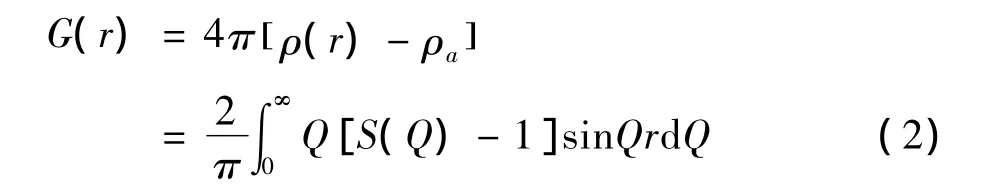
双体分布函数表示为

式中结构函数

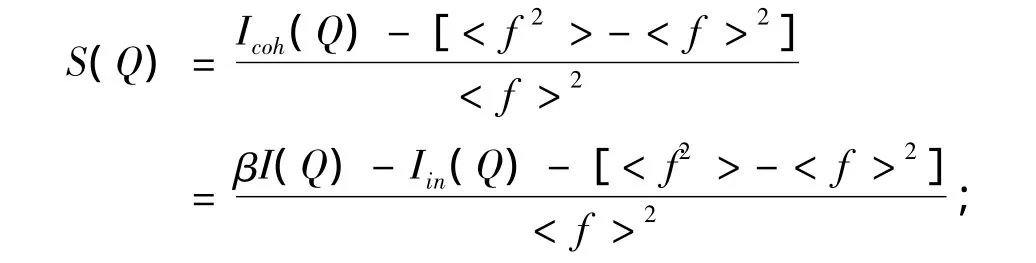
约化结构函数为

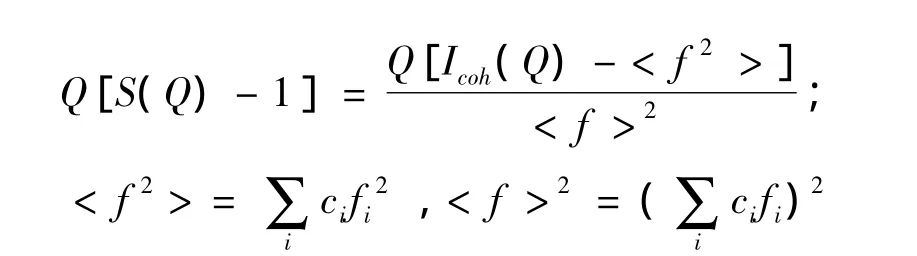
ci和fi分别是各类原子的分数和原子散射因数;Icoh（Q）为一个原子的相干散射强度;β是归一化因子，I（Q）是经过校正后的散射强度，Iin（Q）是非相干散射强度;ρ（r）为原子径向分布的数密度;r为原子径向分布半径;ρa为系统中的平均原子数密度;Q=4πsinθ/λ。

在实际测算时先计算约化径向分布函数G（r），然后再由G（r）计算RDF（r）和g（r）。在计算G（r）时，为消除截止效应影响，要乘以衰减因子e-α2Q2，对 Cu Kα辐射取 α =0.1。

以上过程可以通过IDL程序语言实现，我们利用自编IDL程序进行上述数据处理，得到RDF数据。

2 结果与讨论

2.1 XRD与结构函数分析

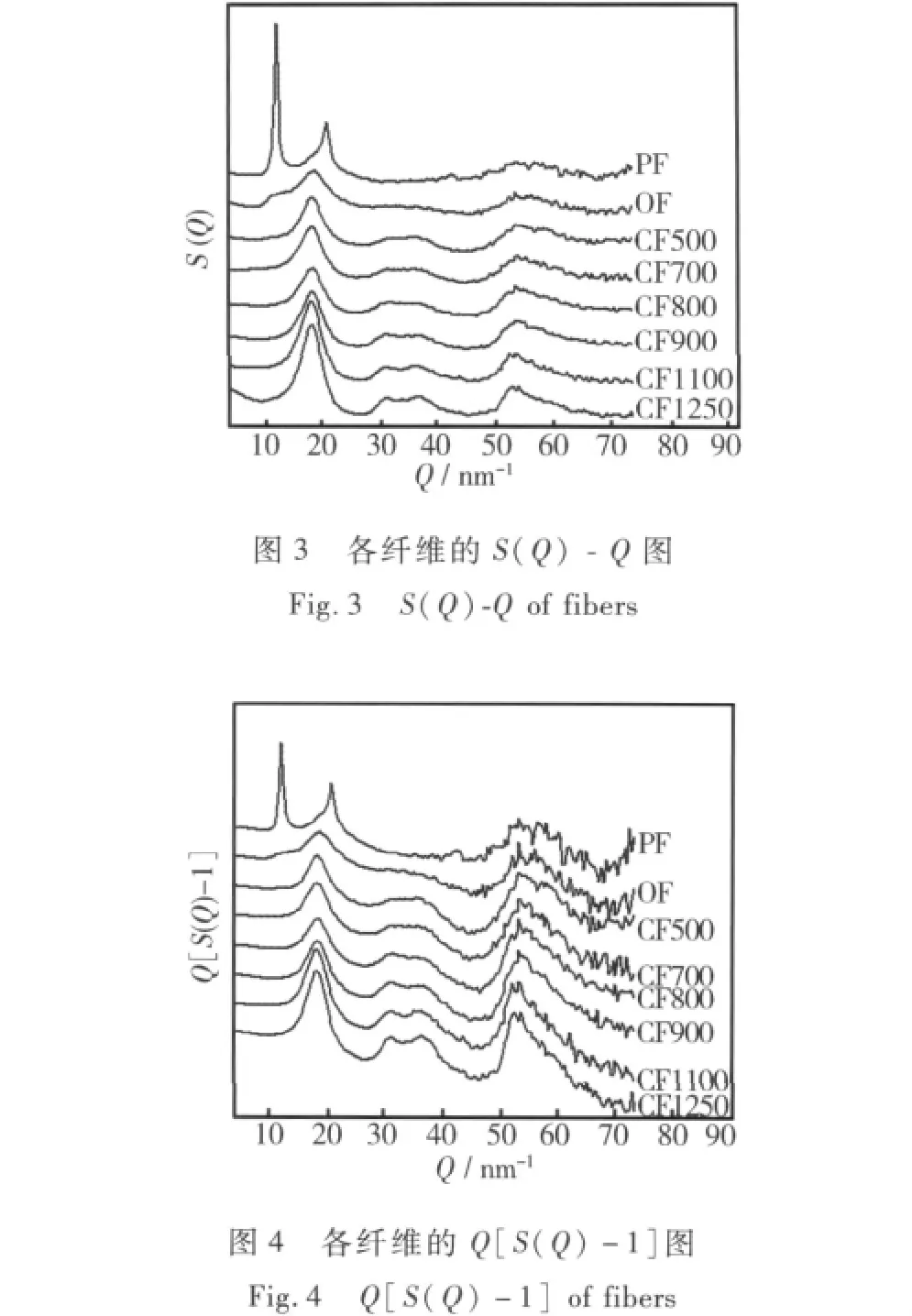
图2为各纤维的XRD原始数据，即I-2θ关系曲线;图3为经校正处理的各纤维结构函数S（Q）曲线;图4为各纤维的约化结构函数Q［S（Q）-1］关系曲线。由图2中可知，PF的衍射曲线在2θ≈17°和 29°处有两个散射峰。OF在2θ≈29°处散射峰消失，而在2θ≈17°处也存在散射峰，但强度很弱，说明其仍保留部分PF的结构信息，但与PF结构存在差异。CF500在2θ≈17°处结构信息完全消失，同时2θ≈25°处出现散射包。在图2中，从CF500到CF1100，各曲线在散射峰形状和强度上的差别都不大，而在图3和图4中，各曲线则有明显差别。该结果表明，与XRD原始数据相比，经过扣除空气散射、吸收和偏振校正、扣除非相干散射以及归一化处理后所获得的结构函数和约化结构函数曲线能更好地反映出各纤维之间的结构差异。从图3和图4中可以看出，PF和OF的结构函数曲线都在Q=18.4 nm-1处有明显的凸起，这与CF500～CF1250碳化纤维中2θ≈25°的散射峰一致。Gupta和Imai等研究者曾将这一弥散峰归因为PAN中的无序非晶结构［15，16］。该结果表明，PAN原丝中已经存在着与石墨类似的结构，该结构是碳化过程中石墨微晶结构形成的基础。因此，作者认为，碳化初期2θ≈25°的弥散峰并不是许多文献所报道的代表新的有序态结构的形成，而是PAN纤维中原本存在的类石墨结构从短程有序向中程有序转变的反映。对于碳化纤维而言，结构函数曲线也更能明显地反映出碳化温度对结构的影响效果。在图3和图 4中，CF1100和CF1250比低温碳化纤维在Q=31.0 nm-1，36.6 nm-1，53.0 nm-1（对应 2θ=44.6°，53.4°，81.0°）附近的散射强度明显增强，散射峰形状趋于尖锐，这些峰分别对应于石墨的（101），（004），（112）晶面，说明碳纤维在大约1100℃的高温碳化阶段石墨化程度显著提高，结构更加有序，出现长程有序结构。

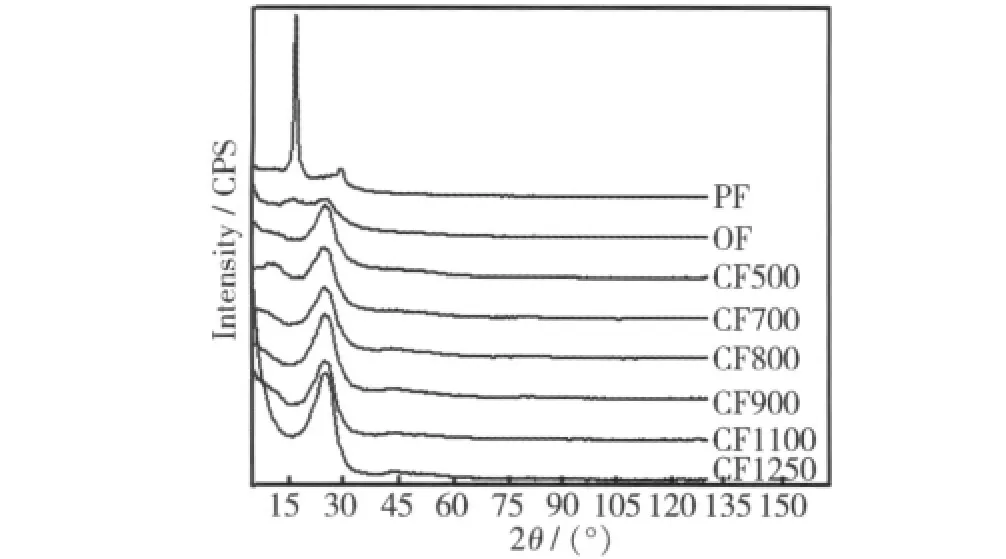
图2 各纤维的XRD图Fig.2 XRD of fibers

2.2 约化径向分布函数分析

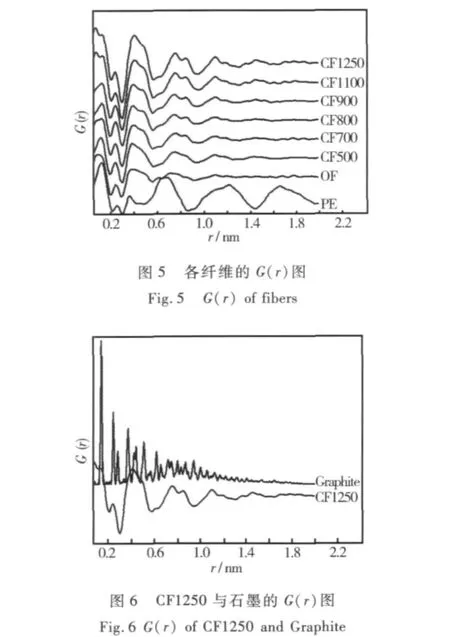
图5给出了约化径向分布函数G（r）曲线，该数据是由约化结构函数经傅立叶变换得到的，图6进一步对比了CF1250与石墨晶体的G（r）曲线，其中石墨晶体的G（r）曲线是由理想石墨的结构参数直接推导得到的。

由图5中可以看出，r在0.1～0.45 nm范围内，曲线呈现三个峰，通过各峰的峰位可获得最近邻、次近邻和第三近邻原子间距离，即r1～r3，结果如表2所示。从PF到CF900，最近邻原子距离都在0.13 nm附近，CF1100和CF1250的最近邻原子距离为0.136 nm，更接近石墨晶体的最近邻原子距离0.142 nm（如图6所示）。除了PF和OF外，其余纤维的次近邻距离（0.246 nm左右）与石墨晶体的次近邻距离（0.246 nm）基本一致，PF和OF的次近邻原子距离分别为0.256 nm和0.252 nm。以上结果表明，在PAN大分子中，G（r）曲线第一峰峰位主要反映主链链内最近邻的C—C原子间距，即平均C—C键长大约为0.13 nm，该数值小于文献中报道到C—C单键键长，主要原因是PAN分子链上强极性基团—C≡N的诱导效应使C—C键长缩短。次近邻距离约等于PAN大分子链内C—C键长的两倍。经过预氧化处理后，发生脱氢、氧化和环化反应，生成了—═CC、—C≡O和—C≡N，一方面这些官能团都会对主链上的未发生反应的C—C单键产生共轭效应使键长缩短，另一方面，主链上也形成了许多—C≡C和—═CN，从而使OF中的平均次近邻距离小于PF。在碳化过程中，线型分子链全部转变成芳构化梯形结构，使碳化纤维的次近邻距离都与石墨晶体的次近邻距离相同。

图5中第三个G（r）峰的峰形随着碳化温度的升高逐渐变窄，该峰是由两三个峰合并而成，其峰位对应石墨晶体中的第4、5、6峰位（如图6所示）。值得一提的是，由图6可得CF1250中没有出现与石墨晶体第三峰所对应的峰。由表2可得，石墨晶体的第三近邻距离为0.284 nm，此距离表征的是平面六元环结构［13］，而所有样品中，直至1250℃碳化纤维中都没有与石墨晶体相同或相近的第三近邻距离，因此，本文推测当碳化温度低于1250℃时，碳纤维中并没有形成平面构型的六元环，可能形成了扭曲的六元环或是五元环、七元环。所有纤维中的第三近邻距离均大于石墨晶体的第三近邻距离甚至第四近邻距离（0.34 nm，对应石墨烯层片与层片之间的距离）。该距离究竟来自于分子链内，分子链间，还是两者的平均结果，有待于结合其它测试方法进一步深入研究。

r在大于0.45 nm范围各纤维之间也出现较明显区别:原丝在此区间有两个明显的宽峰，第一宽峰位置在0.688 nm，与文献报道的PAN大分子链最近邻链间间距（0.611 nm）［17］吻合，此峰反映原丝最近邻链间距离;第二宽峰位于0.121 nm附近，与PAN大分子链次近邻链间间距（0.122 nm）吻合，这一峰反映原丝次近邻链间距离。经预氧化后，这两个宽峰消失，这是因为在预氧化过程中环化、氧化、脱氢等化学反应使原丝结构发生了非晶化转变，原丝的长程有序结构消失，在预氧丝中仅保留了短程和中程有序结构。随着碳化温度的升高，各纤维在r=0.5 nm，0.75 nm，0.85 nm，1.1 nm附近的各峰振幅逐渐明显，特别是CF1100与CF1250在高r（r＞1.1 nm）处，各峰的振幅相比中低温碳化纤维更加明显，这表明在高温碳化阶段，开始出现长程有序结构。

2.3 双体分布函数分析

图7给出了各纤维的双体分布函数g（r）曲线。非晶态材料的近程有序性也可明显地从曲线看出，随着r增大，g（r）曲线趋近于1，原子间的双体相关性逐渐减弱。通常定义g（r）=1±0.02处的r值为有序畴尺寸（rs）。我们选取最大的rs值为有序畴尺寸，实验结果列于表2。原丝PF中存在大量PAN微晶，其有序畴尺寸大于2 nm，预氧丝OF的有序畴尺寸为0.79 nm，经碳化处理后纤维的有序畴尺寸（rs）随碳化温度逐渐变大，表明随温度升高有序程度增加，最终CF1250的有序畴尺寸大于1.2 nm。图8给出了石墨晶体与CF1250的双体分布函数g（r）曲线，可以明显看出r在0.1～0.55 nm反应出的信息与G（r）曲线是一致的;当r＞0.55 nm，与石墨晶体相比，CF1250的各峰振幅明显较弱，而且峰形相对很宽化，g（r）曲线收敛很快，表明且有序畴尺寸远小于石墨晶体，说明在最终1250℃碳化纤维中存在部分长程有序结构，但该结构的结晶完善程度远低于石墨晶体。

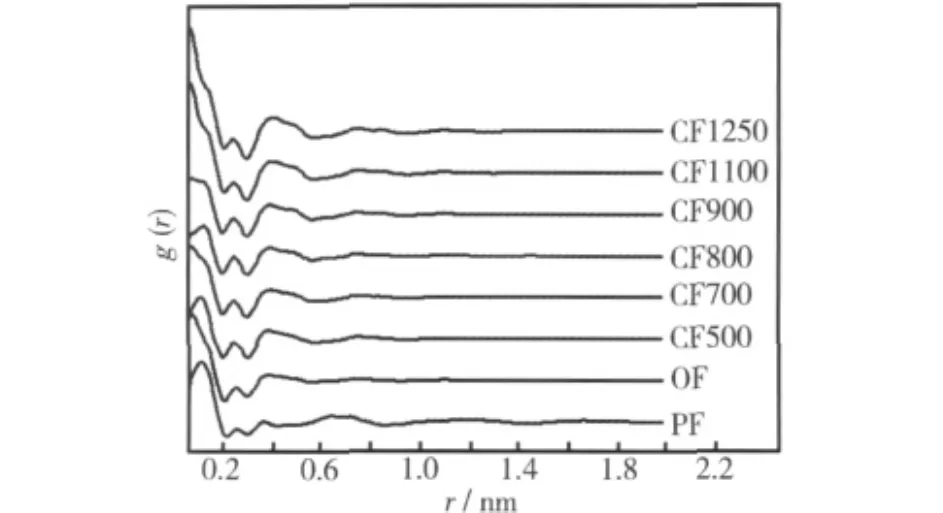
图7 各纤维的g（r）曲线Fig.7 g（r）of fibers

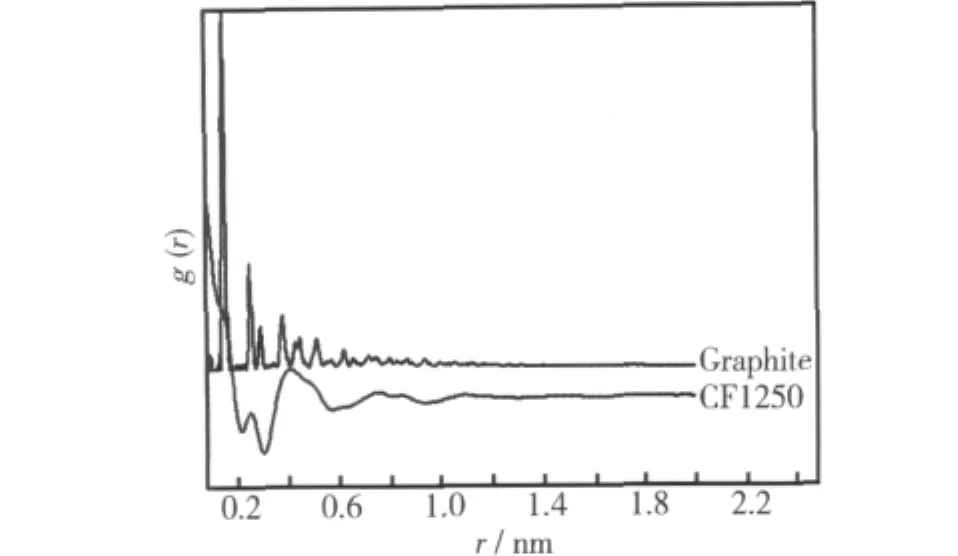
图8 CF1250与石墨的g（r）图Fig.8 g（r）of CF1250 and Graphite

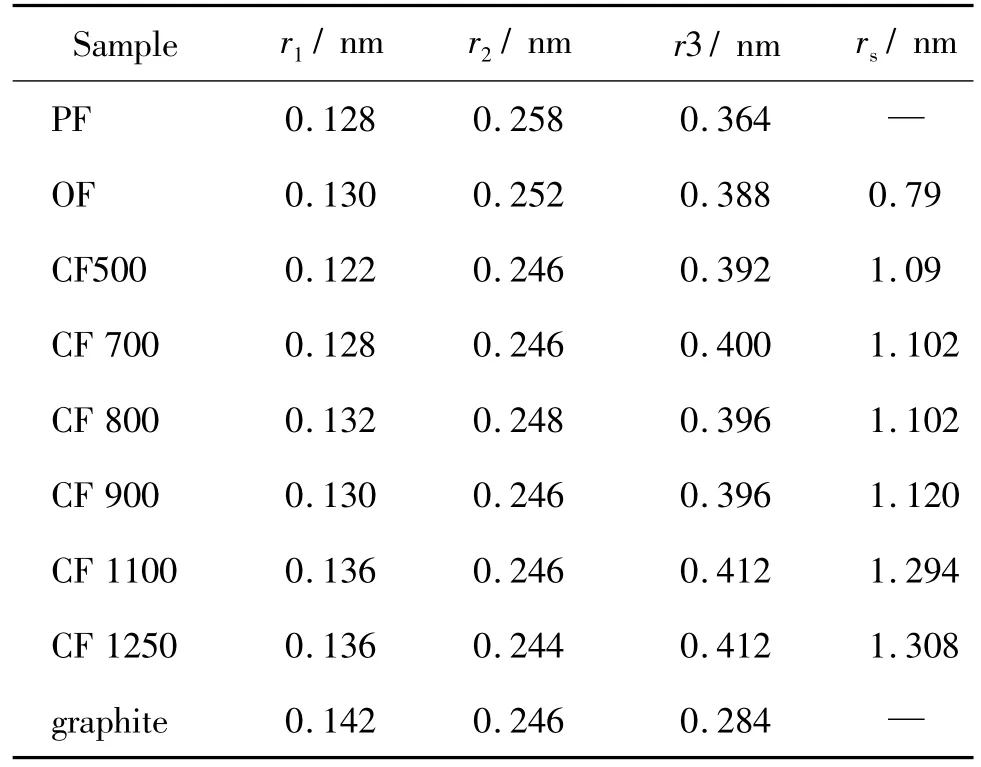
表2 各纤维的原子近邻距离及有序畴尺寸Table 2 Atomic neighbor distance and ordered domain size of each fiber

3 结论

（1）原子径向分布函数能够有效分析碳纤维制备过程中的结构特征及其演变历程。在整个碳纤维的制备过程中，纤维结构经历了长程有序-长程无序、短程有序-长程有序的演变。

（2）结构函数曲线结果表明，PAN原丝在Q=18.4 nm-1处（对应2θ≈25°）的弥散峰代表 PAN纤维中存在与石墨类似的结构，该结构是碳化过程中石墨微晶结构形成的重要基础。

（3）原丝G（r）曲线的第一宽峰位置在0.688 nm，与文献报道的PAN大分子链最近邻链间间距（0.611 nm）吻合，此峰反映原丝最近邻链间距离。

（4）CF500～CF1250所有碳化纤维中的第三近邻距离均大于石墨晶体的第三近邻距离。表明碳化温度达到1250℃时，碳纤维中并没有形成平面六元环的石墨烯层片。

［1］贺福.碳纤维及其应用技术［M］.北京:化学工业出版社，2004.

［2］赵东林，沈曾民，迟魏东.炭纤维及其复合材料的吸波性能和吸波机理［J］.新型炭材料，2001，16（2）:66-72.

（ZHAO D L，SHEN Z M，CHI W D.Radar absorption property and mechanism of carbon fiber and carbon fiber composites［J］.New Carbon Materials，2001，16（2）:66-72.）

［3］李丽娅，黄启忠，张红波.聚丙烯腈炭纤维的组织结构及力学性能［J］.中南大学学报（自然科学版），2005，36（2）:193-197.

（LI L Y，HUANG Q Z，ZHANG H B.Microstructure and Properties of Polyacrylonitrile Carbon Fiber［J］.Journal of Central South University（Science and Technology），2005，36（2）:193-197.）

［4］XU H P，SUN Y P，CHEN X M.Microstructure characterization of PAN preoxidation fibers prepared with radio frequency plasma［J］.Chinese Science Bulletin，2006，51（10）:1255-1260.

［5］刘杰，李佳，王雷，等.预氧化温度对聚丙烯腈纤维皮芯结构形成的影响［J］.北京化工大学学报（自然科学版），2006，33（1）:41-45.

（LIU J，LI J，WANG L，et al.Effect of preoxidation temperature on core/shell structure during the preoxidation procession of PAN fibers［J］.Journal of Beijing University of Chemical Technology（Natural Science Edition），2006，33（1）:41-45.）

［6］季敏霞，王成国.聚丙烯腈基碳纤维制备过程中微观结构的演变［J］.材料导报，2007，21（5）:111-114.

（JI M X，WANG C G.Evolution of Microstructure in the Preparation of PAN-based Carbon Fibers［J］.Materials Review，2007，21（5）:111-114.）

［7］刘福杰，范立东，王浩静，等.高强度炭纤维微观结构分析及力学性能的比较［J］.功能材料，2007，38（10）:1723-1730.

（LIU F J，FAN L D，WANG H J，et al.Study of the microstructure and the mechanical properties of high strength PAN-based carbon fibers［J］.Journal of Functional Materials，2007，38（10）:1723-1730.）

［8］LI F，LANNIN J S.Radial distribution function of amorphous carbon ［J］.Physical Review Letters，1990，65（15）:1905-1908.

［9］SZCZYGIELSKA A，BURIAN A，DUBER S，et al.Radial distribution function analysis of the graphitization process in carbon materials［J］.Journal of Alloys and Compounds.2001，328:231-236.

［10］KUMAR A，LOBO R F，WAGNER N J.Porous amorphous carbon models from periodic Gaussian chains of amorphous polymer［J］.Carbon，2005，43:3099-3111.

［11］HU R Z，EGAMI T.Local intermolecular correlations in C60［J］.Physical Review B.1992，45（16）:9517-9520.

［12］NICHOLAS D M，MARJORAM J R，WHITTAKER O C.Crystallite size effects on the radial distribution analysis of carbon fibers ［J］.Journal of Applied Crystallography，1972，5:262-267.

［13］PETKOV V，DIFRANCESCO R G，BILLINGE S J L，et al.Local structure of nanoporous carbons［J］.Philosophical magazine B，1999，79（10）:1519-1530.

［14］李树堂.X射线衍射实验方法［M］.北京:冶金工业出版社，2000.

［15］GUPTA A K，SINGHAL R P.Effect of copolymerization and heat treatment on the structure and X-ray diffraction of polyacrylonitrile［J］.Journal of polymer science:polymer physics edition.1983，21:2243-2262.

［16］IMAI Y，MINAMI S，YOSHIHARA T，et al.Preparation and characterization of amorphous polyacryloni-trile［J］.Journal of polymer science part B:Polymer letters，1970，8:281-288.

［17］吴宏仁，吴立峰.纺织纤维的结构和性能［M］.北京:纺织工业出版社，1985.