浅谈数控车床加工正弦曲线的方法
2013-07-13刘兴春
刘兴春
(天津市南开区职业中等专业学校,天津 300100)
数控车床是一种高精度高效率的自动化机床,它具有很广泛的加工工艺性能,其加工特点之一就是可以加工轮廓形状很复杂的零件,任意曲线皆可以通过采用用直线插补、圆弧插补逼近的方法来完成加工。
由于数控车床的加工的主体对象是回转体,即圆柱面、圆锥面、圆弧面、圆球面等,这些表面轮廓的加工可以通过直接使用G01(直线插补指令)以及G02/03(圆弧插补指令)来实现,而对于非圆曲线,如椭圆、双曲线、抛物线以及正、余弦曲线等构成的回转体表面,机床本身不能直接用直线插补与圆弧插补直接实现,通常采用拟合法来进行加工,即将复杂曲线用多段的小段直线或圆弧来代替,逐步逼近曲线轮廓,实现对轮廓曲线的拟合,从而完成加工。
完成此类零件的加工,可以采用自动编程实现,即利用计算机专用软件实现工件的编程和加工。但是软件生成的程序通常都很长,产生空刀运行的部分很多,加工时间长,工作效率不高,并且车削加工的工件本身结构相对简单(主要是各类回转面),因而程序也都相对比较简单,往往不需使用软件编程。数控宏程序因其特有的加工灵活性,可以很方便地实现此类非圆曲线表面轮廓的加工。
采用宏程序编程加工非圆曲线轮廓,不仅是现代数控系统一项重要的功能和方法,也是实际生产和数控技能比赛的主要内容之一。通过日常的实习教学和技能训练,现以华中世纪星HNC-21TD/22TD系统数控车床为例,对加工正弦曲线轮廓宏程序的编制方法及实际加工做一探讨。
一、正弦曲线性质概述
由于正弦曲线是同时具有向内凹和向外凸的曲线轮廓,因此不能够采用类似加工椭圆、抛物线或双曲线的编程模式或编程模板,必须要依据正弦曲线的特点选择参数编程。由正弦曲线函数方程y=Asinx可知,其定义域为x∈(-∞,+∞),其值域为|y|≤A,而这里的x值和y值分别对应着机床的Z坐标和X坐标,为方便起见,在这里将正弦曲线方程写为X=AsinZ。正弦曲线的一个重要性质是具有周期性,最小正周期为2π。正弦曲线图像关于坐标原点对称,由图像可知,当Z从-π/2增加到π/2时,sinZ从-A增加到A;当Z从π/2增加到3π/2时,sinZ从A减小到-A,由函数周期性可知,正弦函数在每一个闭区间[-π/2+2kπ,π/2+2kπ](k∈Z)上,单调递增;在每一个闭区间[π/2+2kπ,3π/2+2kπ](k∈Z)上,单调递减。根据这一性质我们可以依据所要加工的曲线实际情况确定曲线的起始角度和终止角度。正弦曲线在闭区间[0,2π]上的图像如图1所示。

图1 正弦曲线
二、正弦曲线宏程序编程思路和方法
1.选定自变量
从理论上讲任何公式曲线中的X坐标和Z坐标均可以被定义为自变量,由正弦函数的性质可知,函数的定义域Z为全体实数,变化范围较大,而函数值域X为[-A,A],变化范围比Z要小很多,因此将Z坐标确定为自变量,亦即选择变化范围大的坐标值作为自变量,在实际练习和技能训练中我们也是将Z坐标确定为自变量。
2.确定自变量的起始点和终止点的坐标
对于正弦曲线而言,其起始点和终止点的坐标均为角度,因为华中世纪星HNC-21TD/22TD数控系统只识别弧度不识别角度,因此这两个坐标值都要用弧度值来表示。坐标值是相对于正弦曲线自身坐标系而言,起点坐标作为初始值,终点坐标作为终止值。由于正弦曲线具有周期性,其起点坐标和终点坐标可以有若干个,如何确定坐标值非常重要,否则会因坐标的选取不当造成零件轮廓加工不准确,甚至是零件报废。经过实践证明,起点的坐标值应当确定在[0,2π]这一范围,终点坐标则根据曲线的周期通过计算得到,并且终点坐标只按照正周期值加起点坐标计算。
如图2所示,该曲线是由两个周期的曲线构成,其起点坐标值确定为π/2,周期值为4π,所以终点坐标值通过计算后得到为9π/2。
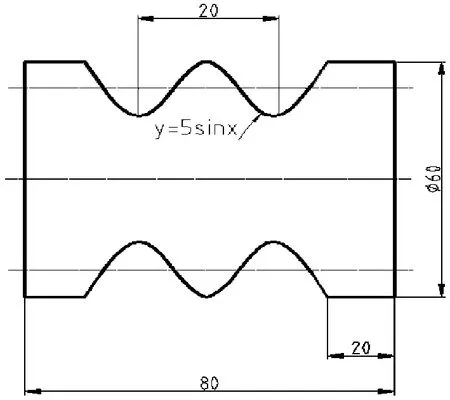
图2 合成曲线
3.进行函数变换,将变量通过自变量的宏表达式表示出来
如图2所示,将自变量Z坐标值设为#1,X坐标作为变量设为#4,则用Z表示X为:X=5*SIN[Z],以宏变量#1、#4分别替换上式中的Z和X,就得到了以自变量表示变量的宏表达式:
#4=5*SIN[#1]。
4.确定正弦曲线起始点的Z向起始值
确定正弦曲线起始点的Z向起始值也是非常重要的,否则会出现加工的曲线轮廓位置不正确。实际训练中,为方便计算,确定该值为0,曲线的实际起始位置可以通过在编程中加以计算得到。
如图2所示,设该曲线Z向起始值#3=0,由于曲线起始点距编程原点距离为20,所以该曲线在实际轮廓中的坐标值通过计算后表示为#3-20。
5.确定Z向增量值
曲线的Z向增量值应根据所加工的轮廓周期长度而定。其计算方法为:曲线加工长度/曲线周期值。

图3 加工图例
要注意的是,这里的周期值应当用角度数值进行计算。如前图所要加工的曲线周期数是2,则该曲线的周期值为720。该曲线的加工长度为40,所以该正弦曲线的Z向增量值应当为:40/720。
以上为宏程序加工正弦曲线轮廓零件的编程思路与编程方法,运用上面介绍的方法,结合数控车削加工循环指令,即可以快速准确的实现正弦曲线轮廓的编程和加工。
三、具体应用实例
如图3所示零件的外轮廓加工程序如下,设毛坯直径为65mm。
该零件加工参考程序如下。
O1234(程序号)
%1234
M03S400T0101(设置主轴转速为400转/分,1号外圆刀具)
G00X66Z1(快速定位到粗加工循环起点)
G73U10R7 W0P10Q20X0.2Z0.1F100(利用封闭车削复合循环指令开始加工)
N10G42GOOX0(精加工起始单节号)
G01Z0
X60
Z-20(正弦曲线加工起点)
#1=PI/2(曲线起始角为#1,曲线起始角度值为PI/2)
#2=9*PI/2(曲线终止角度为#2,曲线起始角度值为9/2 PI)
#3=0(曲线Z向起始值为#3,值设为0)
WHILE[#1]LE[#2]
#3=#3+40/720(计算Z方向值,曲线Z向增量值为40/720)
#4=5*SIN[#1](计算X方向值)
G01X[40+2*[#4]]Z[-#3-20](直线插补)
#1=#1+PI/180(计算Z向弧度值)
ENDW(循环结束)
N20G40G01Z-85(精加工终止单节号)
G00X150Z150(快速定位到安全点)
M05(主轴停转)
M30(程序结束)

图4 加工后的零件
该零件的加工还可以采用G71循环指令进行加工,零件的曲线轮廓形状和尺寸精确度也能够达到要求。不过由于G71循环加工指令的切削进给方向是平行于Z轴逐层切削的,不同于G73指令那样通过刀具逐渐进给,使切削回路逐渐靠近曲线最终形状,最终切削成工件实际曲线轮廓形状,因此在加工时间上G71指令比G73指令要长一些。如果对零件的加工时间要求不是很严格,可以采用G71循环指令进行加工。
加工后的实际零件如图4所示。
四、正弦曲线宏程序的模板设计
通过对以上加工实例的分析,可以将正弦曲线的宏程序编制总结成编程模板如下。
1.程序参数设置
设某一正弦曲线方程为X=AsinZ,其编程参数设置分别为:设起始角为#1,终止角为#2,曲线Z向起始值为#3,曲线Z向增量值为ΔW,曲线X向增量值为#4,曲线中心距为ΔX,曲线起始位置距编程原点距离为ΔZ。
2.编制程序模板
#1=θ0(设置加工起始角度,即Z值)
#2=θ1(设置加工终止角度)
#3=0(设置Z向加工起始值)
WHILE[#1]LE[#2](加工循环设置)
#3=#3+ΔW(自变量步距变化计算,步距值ΔW等于加工长度/周期值)
#4=A*SIN[#1](建立函数关系式,确定X向坐标值)
G01X[ΔX+2*[#4]]Z[-#3-ΔZ](曲线加工)
#1=#1+PI/180(计算弧度值)
ENDW(加工结束)
对于余弦曲线同样可以利用此模板进行编程加工,编程时只需依据所给曲线方程,将模板中相应的公式和角度做简单变换即可。
通过实例加工,我们了解到宏程序加工零件,是通过对变量进行赋值并进行处理后,刀具由工件外不断逼近曲线轮廓形状,直至最终完成曲线的加工。这一方法很好的解决了正(余)弦曲线难以加工的问题,加工出的曲线形状准确,精度高,体现了数控车削加工方便快捷准确的优势。
上述实例在配置华中世纪星HNC-21TD/22TD系统的数控车床上运行良好。如果采用其它数控系统的数控车床,只需根据相应系统指令和语句,简单修改相应的语句后,编程模板即可正常使用。在日常实习教学和技能训练中,加工相同曲线轮廓零件,通过对比自动编程,采用这个编程模板进行编程加工可以节约11分钟左右的时间,由此可见宏程序在加工正(余)弦曲线上所特有的优势。
