弱适当半群的研究

郑 娇， 任学明

(西安建筑科技大学理学院，陕西西安 710055)

J．B．Fountain借助 Green*关系，引入了 rpp半群、富足半群、适当半群和型A半群等概念。这些半群都是广义正则半群的若干重要子类，受到国内外学者的广泛关注。令S为一半群，E(S)为S的幂等元集合。半群S称为rpp半群，如果S的每一L*-类含S的一个幂等元。半群S称为富足半群，如果S的每一L*-类和每一R*-类都含有幂等元。富足半群S称为适当半群，如果S的幂等元集形成可交换子半群，即幂等元集形成半格。

显然，所有的逆半群都是适当的，对于逆半群及适当半群，其性质和重要结论已得到广泛论证［1-2］。在文献［2］中，Howie定义了逆半群S上包含在H中的最大幂等分离同余μ，如下:

μ ={(a，b)∈S × S:(∀e∈E(S))a－1ea=b－1eb}，同时指出S/μ⋍E的充要条件。1977年，Fountain对此结果进行了推广，定义了适当半群S上包含其中的最大同余μ，并给出S/μ⋍E的若干等价刻画。文中将利用广义格林关系(*，～)，定义广义正则半群。这些半群都是适当半群和逆半群在非正则半群类中的共同推广。其中，弱适当半群是r-弱适当半群的子半群，而基本弱适当半群又是弱适当半群的子半群。在此基础上，研究r-弱适当半群，弱适当半群的基本性质和特征。特别地，刻画了弱适当半群上包含于广义格林关系H*，～内的最大同余μ。

1 广义格林(*，～)关系定义

为了陈述方便，首先回顾一下广义格林(*，～)关系的定义［3］:

其中:

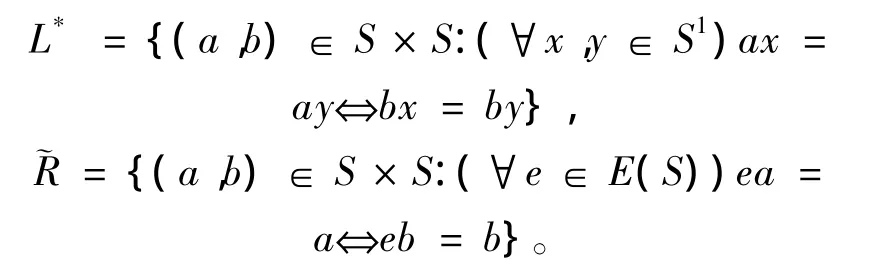
容易验证，L⊆L*⊆。特别地，如果S是正则半群，则L=L*=。如果U是S的一个正则子半群，不难证明:

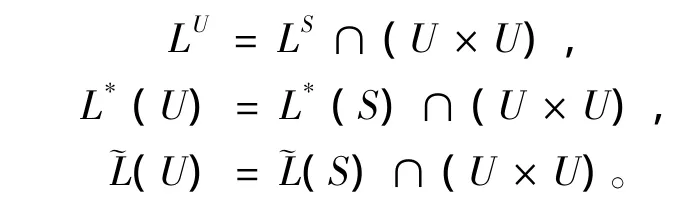
对偶的，可以得到关于关系R的相关结论。

本文未给出的其他概念和记号，见文献［2］和文献［4-10］。

2 弱适当半群定义和特征

定义1 令S为一半群，E(S)为S的幂等元集合。半群S称为r-弱适当半群，如果S的幂等元集形成半格且每一-类都含有幂等元。半群S称为弱适当半群，如果S的幂等元集形成半格且每一L*-类和每一-类都含有幂等元。

命题1 令S为一半群，E是S的幂等元集合，T是S上的正则元集合，则下面各款等价:

1)S是弱适当半群;

2)T是S的逆子半群，E与S的每一个L*-类有非空的交集，E与S的每一个-类有非空的交集;

3)T是S的逆子半群，T与S的每一个L*-类有非空的交集，T与S的每一个-类有非空的交集;

4)S的每一个L*-类和每一个-类有且仅有一个幂等元，同时由E所生成的子半群是正则的。

证 1)⇒2)假设1)成立，则S的每个L*-类和每个-类都含有幂等元。因此，E与S的每一L*-类和每一-类有非空的交集。对于任意a，b∈T，则存在a'∈V(a)，b'∈V(b)，使得aa'a=a，bb'b=b。进一步得

因此ab是正则的，即ab∈T。由此可证，T是S的子半群。又因为T是正则的且幂等元可换，所以T是S的逆子半群。

2)⇒3)如果2)成立，根据E⊆T，3)也成立。

3)⇒4)如果3)成立，令L是S的一个L*-类，则有(∃a∈L∩T)(a－1a，a)∈LS，这里，a－1∈V(a)且a－1唯一，则每一L*-类含有唯一的幂等元。令R是S的一个-类，则(∃b∈ R ∩ T)(b－1b，b)∈ RS。这里，b－1∈V(b)且b－1唯一，因此每个-类只含有一个幂等元。因为T是逆半群且E⊆T，则E形成半格，则 E=〈E〉。显然 E ⊆〈E〉。令 a∈〈E〉，得(∃e，f∈E)a=ef，a2=(ef)(ef)=ef=a。由此可知a∈E。因此 E=〈E〉。

4)⇒3)只需证明E可形成半格。因为E所生成子半群是正则的，则〈E〉的每一个L-类和每一个R-类有且仅有一个幂等元。因此〈E〉是逆半群。不难证明E=〈E〉，所以E可形成半格。

注意到，如果S是弱适当半群，则每一个L*-类和每一个-类只含有一个幂等元。令a∈S，把a所在的L*-类中的唯一幂等元记为a*，a所在的-类中的唯一幂等元记为a+。

引理1［3］令S是一个半群，则下面各款成立:

1)L*是一个右同余;

命题2 令S为一弱适当半群，E为S的幂等元集合。则对任意a，b∈S，下面各款成立:

1)aL*b⇔ a*=b*，a~Rb⇔a+=b+;

2)(ab)*=(a*b)*，一般地，(ab)+≠(ab+)+;

2)因为(a，a*)∈L*且L*是S上的一个右同余，则(ab，a*b)∈ L*，因此(ab)*=(a*b)*。

4)显然。

3 主要结果及其证明

令S是一弱适当半群，E为幂等元集合。则包含在L*的最大同余μL*定义为

其中αa是从E1到E1的映射，对任意的x∈E1，有xαa=(xa)*。

为了证明下面的命题，首先定义映射β:S→Γ(E1)为

这里βa:E1→E1定义为

接下来证明映射 β 满足等式(aβ)(bβ)=(ba)β。令x ∈ E1，a，b ∈ S。 则 xβaβb= (ax)+βb=(b(ax)+)+=(bax)+=xβba。因此 βaβb= βba。

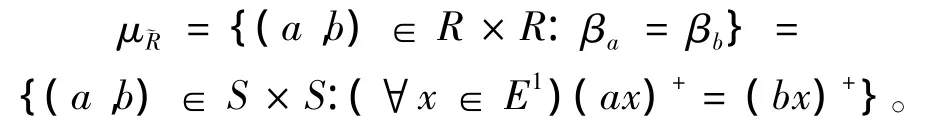
证 显然，μ是等价关系。令a1，a2，b1，b2∈S。如果(a1，a2)∈ μ，(b1，b2)∈ μ，则 βa1= βa2，βb1=βb2。因此 a1β =a2β，b1β =b2β。进一步得

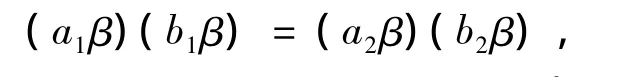
即(b1a1)β =(b2a2)β，即 βb1a1= βb2a2。由 μR的定义知，(b1a1，b2a2)∈ μ，因此 μ~R是一个同余。令(a，b)∈ μ，则 a+=b+。因此(a，b)∈，即 μ⊆。

证 令a，b∈S，a+=b+，且对于任意的x∈a+E满足(xa)*=(xb)*。则对于任意的y∈E有(ya+a)*=(ya+b)*=(yb+b)*=(yb)*。所以，(a，b)∈μL*。另一方面，如果 a*=b*，且对于任意的y∈a*E，满足(ay)+=(by)+，则对于任意的x∈E，有(ax)+=(aa*x)+=(ba*x)+=(bb*x)+=(bx)+。所以(a，b)∈ μ。

对于右适当半群S，如果满足μL*=l，则称S是右基本的。下面给出基本弱适当半群的定义。

定义2 令S是一弱适当半群，则S称为是基本的，如果 μ =l。

证 由推论1可得，存在某元素 e∈ E，使得(aμ)*=eμ。利用等式(aμ)(a*μ)=(aμ)(eμ)=aμ，可以得到(eμ)(a*μ)=eμ，即(ea*，e)∈ μ，则ea*=e。另一方面，(a，ae)∈ μ，μ ⊆ μL*，所以，a*=(ae)*=a*e，即e=a*。同理可得，存在某元素 f∈ E，使得(aμ)*=fμ。因为(a+μ)(aμ)=aμ =(fμ)(aμ)，则有(a+μ)(fμ)=fμ，即(a+f，f)∈μ，a+f=f。另外，从aμ =(fμ)(aμ)可以看出，(a，fa)∈μ;又因为μ⊆μ，则a+=(fa)+=fa+，即f=a+。综上，命题得证。

当S是弱适当半群时，可以考虑把αa，βa的前域分别限制在集合a+E和集合a*E上，则

αa:a+E→a*E定义为

eαa=(ea)*(e∈ a+E);

βa:a*E→a+E定义为

eβa=(ae)+(e∈ a*E)。

(∀x ∈ a+E)xαaβa≥ x，(∀y ∈ a*E)yβaαa≥ y。

证 如果x∈a+E，则xαaβa=(a(xa)*)+。又因为x(a(xa)*)+=(xa(xa)*)+=(xa)+=xa+=x。

所以 xαaβa≥ x。同理，yβaαa≥ y。

定义3 弱适当半群S称为是弱型A半群，如果

(∀a∈ S，e∈ E)ea=a(ea)*，ae=(ae)+a。

1)S是弱型A半群;

2)映射 αa，βa是单射。

证 1)⇒2)假设S是弱型A半群，令a∈S，e，f∈a+E。如果 eαa=fαa，则(ea)*=(fa)*，则 ea=a(ea)*=a(fa)*=fa。因此 e=ea+=(ea)+=(fa)+=fa+=f，可见 αa是单射。同理，不难证明 βa也是单射。

2)⇒1)假设对于任意a∈S，映射 αa，βa是单射。令 x∈ a+E 且 e=xαaβa。由映射 αa，βa的定义，易证e∈a+E。再根据引理3，进一步可得x≤e。因为(ea)+=ea+=e，因此 dom αea=eE。同时有

xαeaβea=xαeαaβaβe=xαaβaβe=eβe=e，eαeaβea=eαeαaβaβe=(eαaβa)βe=(eαaβa)βee=e。注意到 αea，βea都是单射，则 e=x。因此 αaβa=1a+E。同理可证 βaαa=1a*E。

令 p=ea+∈ a+E，则 pαaβa=(a(pa)*)+=p，则

ea=ea+a=pa=(pa)(pa)*=

(a(pa)*)+a(pa)*=a(pa)*=a(ea)*。

令 q=a*e∈ a*E，则 qβaαa=((aq)+a)*=q，则

ae=aa*e=aq=(aq)+aq=(aq)+a=

((aq)+a)*=(aq)+a=(ae)+a。

综上所述，S是弱型A半群。

［1］Fountain J B．Adequate semigroups［J］．Proc Edin Math Soc，1979，22:113-125．

［2］Howie J M．An introduction to semigroup theory［M］．London:Academic Press，1976．

［3］GUO Y Q，Shum K P，Gong C M．On(* ，～)-Green`s relations and ortho-lc-monoids［J］．Communications in Algebra，2011，39:5-31．

［4］Fountain J B．Abundant semigroups［J］．Proc London Math Soc，1982，44:103-129．

［5］Lawson M V．The structure of type A semigroups［J］．Quart J Math Oxford，1986，37(2):79-298．

［6］Ren X M，YANG D D，Shum K P．On locally ehresmann semigroups［J］．Journal of Algebra and Its Applications，2011，10(6):1165-1186．

［7］REN X M，Shum K P．The structure of-inverse semigroups［J］．J Algebra，2011，325:1-17．

［8］REN X M，Shum K P，GUO Y Q．A generalized clifford theorem of semigroups［J］．Science China Ser A，2010，53(4):1097-1101．

［9］REN X M，WANG Y H，Shum K P．On U-orthodox semigroups［J］．Science in China Ser A，2009，52(2):329-35．

［10］Fountain J B．A class of right PP monoids［J］．Quart J Math，1977，28:85-300．