基于最优熵滤波器的非线性非高斯带有数据缺失随机系统的故障隔离
2013-07-07温东宾张正道
温东宾, 张正道, 潘 丰
(江南大学轻工过程先进控制教育部重点实验室,江苏无锡 214122)
近年来,随机分布系统的故障检测与隔离问题成为研究的焦点,也提出了许多有效的解决方法。大体可分为如下两类[1-2]:一是使用统计学理论,例如似然函数和贝叶斯理论,再结合诸如蒙特卡罗方法、粒子滤波器等的数学计算,对故障(或系统参数突变)进行预估;二是基于特定方法的滤波器,例如最优化熵滤波的最小化思想,能使估计误差满足各项性能指标[3]。
在研究线性高斯系统的故障检测与隔离时典型的方法是卡尔曼滤波器(KF)及改进(EKF)。而对于非线性系统,滤波器的设计还需要一定的变换或逼近,以使得误差方程满足一定的线性结构[4]。尽管如此,系统会受到高斯噪声的影响,可能产生非高斯的输出信号。对于一个非高斯的参数,均值和方差均不能有效表征其动态特性。此时,改进的卡尔曼滤波器也只能在一定范围内使用,因为它仅仅给出了一个最小化参数估计[5]。熵能权衡随机特性,广泛应用于信息、热力学和控制理论中。在文献[6-7]中,用B样条原理逼近系统输出的概率密度函数,随机故障检测与诊断问题转变成由线性系统支配的动态权重选择问题。文献[8]给出了一种使用可测的输出概率密度函数的鲁棒性故障检测与诊断方法,解决了一类非线性系统的动态权重模型。但是,文献[9]的计算过程过于繁琐,结论需要满足假设:(1)输出信号可测;(2)输出的概率密度函数能用B样条原理近似逼近;(3)控制输入量与在线权重之间的动态权重可建模。
从实际情况出发,有两类故障隔离问题需要考虑:第一类是输出信号可测情况;第二类是输出的数据有部分缺失情况。针对第一种情况的方法,假设分析的采样数据集是完整的,可以通过构建一个残差滤波器;然后,基于熵最优化准则(EOP)对该滤波器的残差故障检测性能优化,其目的是将目标故障与非目标故障进行分离;最后,为了简化过程的计算量,引入辅助映射和Renyi熵来计算误差的概率密度函数。第二类情况反映实际工业过程当中,采集到的数据不完整。引起缺失数据的原因很多,如观测器故障、观测器观察范围之外的误差、数据采集系统故障、计算机系统崩溃、中断的输电线路、本地数据的错误格式化、管理软件的数据错误以及数据备份的故障等。有时,数据在关键位置的值无法获得,其原因归咎于观测器或采样的问题,例如分析仪器的采样频率与温度、流速、压力的测量频率相比过低。对于这类情况下的故障隔离问题,目前的成果依然较少。
文中主要提出一种非线性非高斯带有数据缺失的系统故障隔离方法。首先利用EM迭代算法修补缺失的数据,然后基于数据驱动模型的思想设计最优化熵滤波器,实现目标故障的隔离作用。利用一个数据缺失示例,验证了该方法的有效性。
1 对象模型和故障隔离问题
1.1 对象模型
构建非线性非高斯动态离散系统的差分状态方程和输出动态方程:

其中:xk为系统k时刻的状态量;δk为需要隔离的目标故障;ηk为非目标故障,由系统方程建模误差引起;ωk为干扰的噪声信号;vk为干扰输出yk的噪声信号。δk,ηk,ωk,vk为有界的、互为独立的随机变量。假设1 f(·)和h(·)是两个已知的波尔可测和非线性平滑函数,初值 f(0,0,0)=0;
假设 2 外部输入 δk,ηk,ωk,vk是有界、互为独立的随机变量,且各自的概率密度函数已知。初始时刻x0是一个概率密度函数已知的随机变量。
1.2 动态误差和故障隔离滤波器
依据非线性非高斯系统参数模型,构建如下的滤波器参数模型:

其中,Uk为滤波器控制增益,状态误差表达式:ek=xk-k,则

定义系统残差:êk=h(xk,vk)- h(k,0)。
由假设1的内容可知,系统残差可写成:

其中,Lk为确定的常量;ρk(xk,k)为由状态误差引起的不确定量;êk与误差ek成线性关系。ρk(xk,k)∈[M1,M2],因此残差的熵满足不等式:
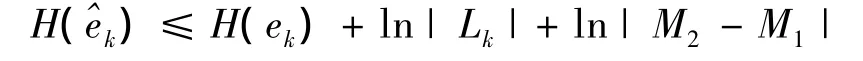
通常情况下,yk是可测的,误差ek+1可看成是Uk的参数表达式。设计适当的Uk,使误差ek+1受目标故障 δk的影响最大化,而受变量 ηk,ωk,vk的影响最小,实现目标故障δk隔离。本中与参考文献不同之处在于:yk是部分数据缺失的,且yk概率密度函数未知。文中主要考虑离线系统的故障隔离问题,先修补缺失数据,然后计算yk的概率密度函数,为最优化熵滤波器设计做准备。依据引言的两类实际情况进行分析讨论:
Case 1:yk任意时刻可测。
方程式3的误差ek+1可以看作两部分组成:
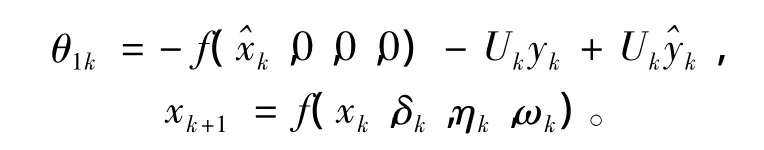
由假设 2 已知,xk,δk,ηk,ωk是互为独立的变量,其概率密度函数已知,所以xk+1的概率密 度函数表达式:
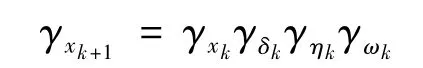
假设2给定x0、目标故障、非目标故障及噪声的概率密度函数,经过k次迭代积分,获得xk+1的概率密度函数:

定义积分区域:假设τ是给定的常数:

因此,状态误差ek的概率密度函数写为
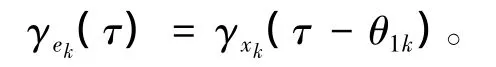
Case 2:yk数据缺失。
首先,需要对缺失数据yk使用EM算法,然后计算概率密度函数γyk。EM算法需要以下几个步骤:
1)初始化分布参数;
2)重复E-Step和M-Step直至收敛。
E步骤:估计未知参数的期望值,给出当前的参数估计。
M步骤:重新估计分布参数,以使得数据的似然性最大,给出未知变量的期望估计。
在迭代收敛过程,缺失数据使用估计值修补完整。令

由方程式5的关系可知:

在上述条件下,动态误差的概率密度函数的表达式为 γek(τ)= γdk(γ - θ2k)。
证 状态误差ek+1=dk+1+θ2k。
方程式(5)给出了 dk+1是 f(xk,δk,ηk,ωk)和Ukyk两个随机变量的求和。利用方程式(6)可得γdk+1(τ),又因为 ek+1=dk+1+ θ2k,所以
γek(τ)= γdk(τ - θ2k)。
证明完毕。
显然γek(τ)可以用5个互为独立的概率密度函数 γδk(τ),γηk(τ),γωk(τ),γvk(τ),γxk-1(τ)和 Uk来表示,是一个在其积分区域Ωk上的多重积分。
2 最优化熵滤波器
2.1 最优化熵原则
定义状态误差ek的熵为

因为 γek(τ)是可用 γδk(τ),γηk(τ),γωk(τ),γvk(τ),γxk-1(τ)和Uk表示,所以 H(ek)也可用它们的熵来表示。实际上,H(ek)是关于5个变量的条件概率。
因为滤波器的目的是隔离目标故障,所有状态误差分成两部分:目标故障引起的误差e1k+1和非目标故障引起的误差e2k+1。先考虑Case 1,两部分对应的参数表达式:
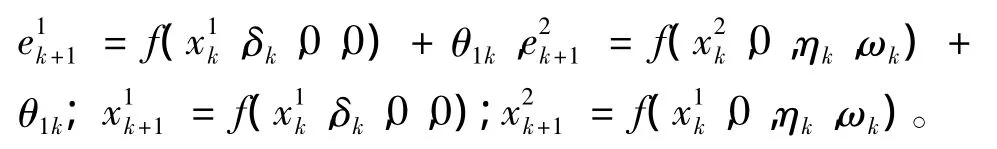
定理1

积分区域:假设给定常数τ。
Π1:={(τ1,τ2)|f(τ1,τ2,0,0)≤ τ},
Π2:={(τ1,τ2,τ3)|f(τ1,0,τ2,τ3)≤ τ}
对于Case 2,同理可得,由方程式(6)可知:

定理2 Case 2对应的概率密度表达式为

其中



2.2 优化算法
假 设 3 xk∈ [a,b] 取 任 意 值 时:∂f(xk,δk,ηk,ωk)/∂xk≠0 均成立。
给定一个常数 τ,对于 f(τ1,τ2,0,0),f(τ1,0,τ2τ3),f(τ1,τ2),f(τ1,τ2,τ3)有可逆函数,其中:
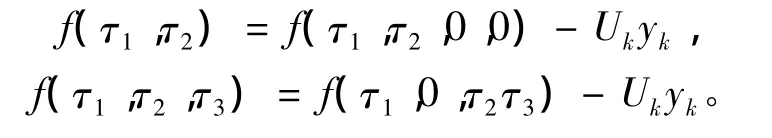
由可逆函数的定义可知:

构建如下的多维辅助映射:

定理3 对于Case 1,利用假设1~3,则在t=k时,的概率密度表达式:

其中
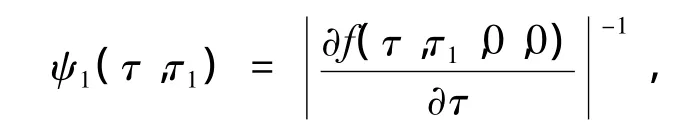

得出误差的概率密度表达式为
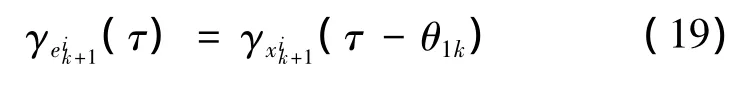
证
由方程组(16)的第一个方程可知:


将上式代入式(20)即可证明。
定理4 对于Case 2,利用假设1~3,在t=k时,状态误差的表达式为


ψ1(τ,τ1),ψ2(τ,τ1,τ2)在定理 3 中已经给出。先代入式(11),然后代入式(21),求得误差的概率密度函数。
2.3 最优化熵滤波器设计
Renyi熵定义:

当α=2时,

最大则须H2(ek)取最小化。因此,考虑如下的瞬时代价函数:

令∂Jk/∂Uk=0获得的控制增益Uk,进行如下的公式变形:

在Uk-1处对Jk(Uk)进行泰勒级数展开:
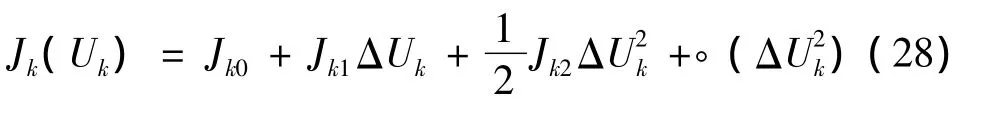
其中

定理5 对于Case 1的故障隔离,最优滤波器控制增益:

设定初始值,在任意k时刻的控制增益,状态误差的概率密度函数通过以下实验仿真步骤获得:
1)定义初始时刻的参数值x0,0,U0及初始化分布参数;
2)重复3)和4)步骤直至收敛,跳至5);
3)E步骤:估计未知参数的期望值,给出当前的参数估计;
4)M步骤:重新估计分布参数,以使得数据的似然性最大,给出未知变量的期望估计;
6)根据定理4,求得该时刻的误差表达式,关于Uk的一个多项表达式;
7)式(27),(29),(30)及

求得t=k时刻的Uk,ΔUk;
8)k=k+1≤N,返回到5),否则到9);
9)绘制状态误差ek。
3 实验仿真
为了故障隔离的仿真,非线性非高斯参数模型:

其中目标故障δk的概率密度函数(见图1)表达式:

非目标故障ηk的概率密度函数(见图2)表达式:
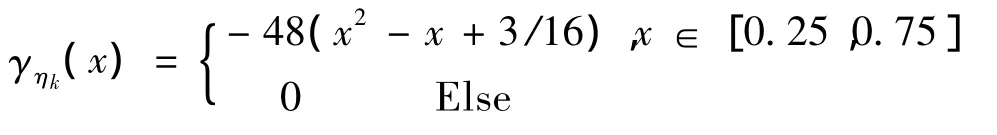
干扰信号wk的概率密度函数表达式:

vk为服从N(0,1)的高斯变量。
根据方程式2,故障隔离滤波器设计为
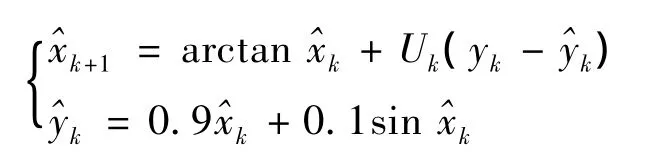

在仿真中,权重系数R1=1,R2=20,设定的初始值为 U0=0,0=0,x0是一个在区间[0,1]上的均匀分布,即概率密度函数为1。按照2.3节中滤波器设计的迭代步骤,得到图3,4。图3为只存在目标故障δk的系统状态误差的动态响应;图4为只存在ηk影响下系统状态误差的动态响应。

图3 存在目标故障时的误差响应Fig.3 Response when the target fault occurs

图4 只存在非目标故障时的误差响应Fig.4 Response when the nuisance fault occurs
图3,4仿真是针对Case 1的仿真结果。显然在数据完整的情况下,故障隔离目标故障的效果较好。对于 Case 2,预计对y值依次采用5%,10%,20%的缺失情况进行EM修补并故障隔离仿真,图5,6,7是目标故障隔离的仿真。
故障的发生时间、振动幅值可以清晰观测得到,为了分析数据方便,构建表1进行对比描述。从表1可以看出,缺失5% 的数据时,系统故障隔离仍能发挥作用,但是有1.112 s的时间延迟,这是数据修补算法过程带来的时间消耗。图6反应因为缺失数值过大,误差相应的幅值开始变大,时间延迟更加增大(延迟2.451 s)。图7因为缺失数值达到了20%,故障隔离已经无法准确地判断故障发生的时刻,且因为误差振幅过大,影响故障信号的检测。图8,9,10是非目标故障仿真示意图,通过详细观察对比可以发现幅值和信号跳变时刻的改变。
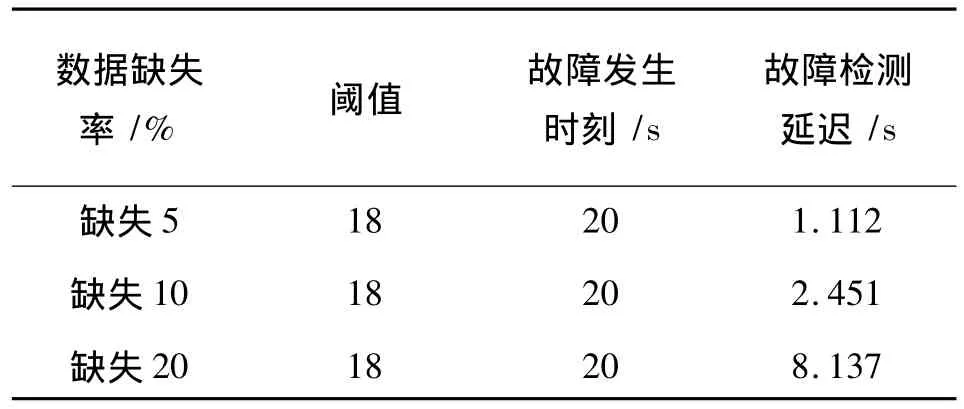
表1 图5,6,7的仿真结果比较Tab.1 Comparative simulation result of Fig.5,6,7
为了便于说明,建立表2分别对故障的发生时刻与振幅变动加以对比分析。从表2的数据可以看出,图8为5% 的数据缺失,非目标故障发生时刻有1.176 s的延迟,且平稳状态时的幅值波动增大;图9为10% 的数据缺失,故障检测的时延增大为2.578 s,误差波动的幅值更加剧烈;图10为20%的缺失数据,误差的幅值波动过大,与非目标故障的幅值接近,无法进行故障检测。


非目标故障的隔离在y缺失5%,10%,20% 时的仿真可以看出,与目标故障隔离相同的实验结论,随着缺失数据的增大,误差幅值渐渐增大,故障检测延迟越来越大,直到数据缺失20%,非目标故障抑制作用失效。

表2 图8,9,10的仿真结果比较Tab.2 Comparative simulation result of Fig.8,9,10
4 结语
在现有故障隔离方法的基础上,提出了在输出信号Y存在数据缺失的故障隔离问题。首先,使用EM算法,通过E-Step和M-Step迭代直至收敛,得到的估计值填补到缺失集合内。其次,基于修补完整的数据驱动模型,构建滤波器,可实现对系统状态的估计。然后,状态误差由非线性非高斯系统模型和滤波器模型来表达,其关系用概率密度函数表达,再对概率密度函数用最优化准则进行优化,通过迭代优化,可使得目标故障存在时状态误差概率密度函数的熵最大化,同时保证在只有非目标故障时最小化,实现目标故障的隔离作用。
文中仍然具有一定的局限性,EM算法是假设缺失以随机缺失机制,修补方法的好坏,影响着基于数据驱动的滤波器设计,进而影响故障隔离的效果。
[1]周靖林,岳红,王宏.基于有理平方根B样条模型的概率密度函数形状控制[J].自动化学报,2005,31(3):343-351.ZHOU Jing-ling,YUE Hong,WANG Hong.Shaping of output PDF based on the rational square-root B-spline model[J].Acta Automatica,2005,31(3):343-351.(in Chinese)
[2]ZHOU J L,WANG H.Optimal tracking control of the output probability density functions:square root B-spline model[J].Control Theory and Applications,2005,22(3):369-376.
[3]YUE H,WANG H.Recent developments in stochastic distribution control:a review[J].J Meas Control,2003,36(7):209-216.
[4]GUO L,YIN L P,WANG H,et al.Entropy optimization filtering for fault isolation of nonlinear non-gaussian stochastic systems[J].IEEE Transactions of Automatic Control,2009,54(4):804-810.
[5]GUO L,WANG H.Minimum entropy filtering for multivariate stochastic systems with non-gaussian noises[J].IEEE Transactions on Automatic Control,2006,51(4):695-700.
[6]WANG H.Bounded stochastic distributions control for pseudo ARMAX stochastic systems[J].IEEE Transactions on Automatic Control,2001,46(3):486-490.
[7]WANG H.Fault diagnosis and fault tolerant control for non-gaussian stochastic systems with random parameters[J].Springer Tracts in Advanced Robotics,2003(1):59-84.
[8]XU Zheng-guo,JI Yin-dong,ZHOU Dong-hua.A new real-time reliability prediction method for dynamic systems based on on-line fault prediction[J].IEEE Transactions on Reliability,2009,58(3):523-538.
[9]LI T,GUO L.Optimal fault-detection filtering for non-Gaussian systems via output PDFs[J].IEEE Transactions on Systems,Man and Cybernetics A,2009,39(2):476-481.
