CVT动力系统中的换档速度控制

1 前言

由于发动机特性存在全功率运转的可能性，无级变速器（CVT）构成动力系最有利的解。该系统的控制已经有数值理论和实际研究论述（Boos和Vorndran，1994；Fujii和 Kanchara，1993；Ide，2000；Jantos，2001；Laan 和 Luh，1999；Dsamura 等，2001）。对于一常车辆速度，传动系速比选择的基本准则包括动力系的运转效率

上式可明确表示发动机的运转效率（ηe）和动力系机械效率（ηCVT）的乘积，它通常与CVT的效率成比例（Akehust等，1999；Förster，1991；Holloway，1999；Kim和Lee，1994）。解决包含瞬时状态发生的控制问题的障碍是必需在尽可能最短时间内，增加驱动从动车轮的功率，而这种改变还要保持平稳进行。该结果构成数值理论和实验研究课题（Holloway，1999；Jantos，2001；Koch和Zeller，1987；Mamala等，2007）。此外，有许多有趣的工程设计，用一附加的机械动力源，目的在于功率的瞬时储存（Akehust等，1999；Boos和 Vorndran，1994；Fujii和 Kanehara，1993；Jantos，2001；Kim 和 Lee，1994；Vroemen和Veldpaus，2000）。但是该问题还没有一个最终的满意方式的解。本文开发了由于瞬时过程造成传动系速比改变时，作用于车轮上驱动力的控制的讨论。

2 驱动功率增加

汽车中传动件的输出功率可以由转矩（Te）和曲轴的角速度（ωe）的乘积确定

在此公式的基础上，驱动功率的增加值可写成

对于该情况，当必需增加曲轴角速度时，应考虑计入发动机回转质量的机械惯量。因此，为进一步分析的需要，提出一个动力系的物理模型（图1），其中采用独立当量机械发动机惯量（Je）。

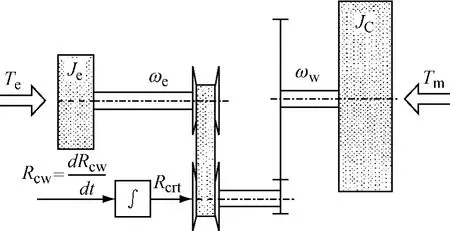
图1 采用独立机械发动机惯量动力系模型：RCVT—CVT速比，ωW—车轮速度，JC—归并入从动车轮轴的机械车辆惯量Fig.1 Powertrain model with isolateed mechanical engine inertia：RCVT—CVT ratio，ωW—wheel speed，JC—mechanical car intertia reduced to axis of the driven wheels

对于这种形式模型，从发动机传到传动系功率可写成

由于汽车运行平稳性的要求建立一个假定，传递到传动系的功率在汽车运行阻力下不可任意瞬时下降（防止汽车的负加速度）。在这种情况，为采用全发动机转矩（T100），曲轴瞬时角加速度为

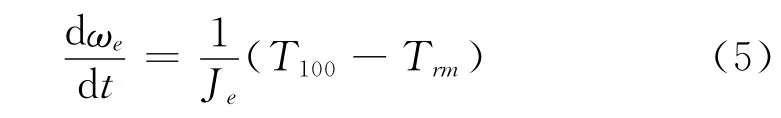
式中Trm：转化至发动机曲轴的汽车运行（滚动和拖曳）的阻力矩。

3 CVT控制

本分析对象是采用机械的CVT，其中转矩利用摩擦力传递（图2）。

需要的轴向力（A）是由应用—液压装置造成的带轮对带侧面所必需的推力（图3）。

为CVT长寿命和机械效率的目的，该轴向推力的大小应该是可调的。图3示解决压力方面，传动中各带轮只有一个工作油缸，故该压力在传动中碰到有一确定的传递转矩和速比的边界值。

在静止状态，传动装置不承受负载，轴向推力相除关系为

图2 CVT图：具有轴向夹紧力的驱动带轮和（b）CVT基本几何参数：r—传动轮的半径；a—传动轮的中心距，α—接触角Fig.2 Diagram of CVT：（a）driving pulley with axial clamping force and（b）basic geometrical parameters of the CVT：r—radius of the transmission wheels，a—distance of transmission wheels，α—angle of contact

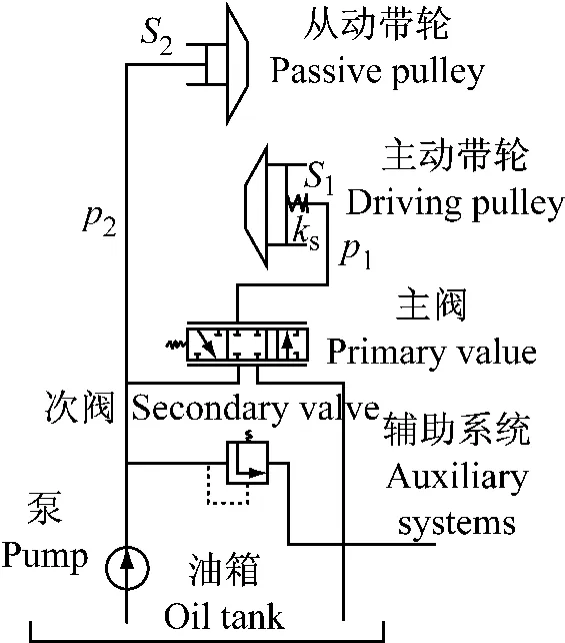
图3 CVT内的液压装置：S—带轮推力面，p—液压装置内油缸油压，ks—弹簧刚度Fig.3 Hydraulic system in CVT：S—thrust surface in the pulleys，p—cylinders oil pressure in the hydraulic system，ks—spring rate

用该关系式表示CVT（RCVT）的运动速比

式中K：与传动装置基本几何参数有关的系数

式中L：CVT中带工作长度，m。

在非静止状态，传动装置的动特性可以近似采用一微分方程（Ide，2000；Jatos，2001）来描述

式中ξ：推力比的瞬态值。

δ：有关传动系工作状况系数。

4 采用CVT汽车的纵向动力学研究

根据以上理论研究，其结果合理解决了加速时，轿车瞬态过程有关必需分析的动力系CVT控制问题。为此目的，计划好一加速和按常速起动和加速踏板激剧和全压低的道路试验。该运行试验的轿车采用的基本参数列于表1。

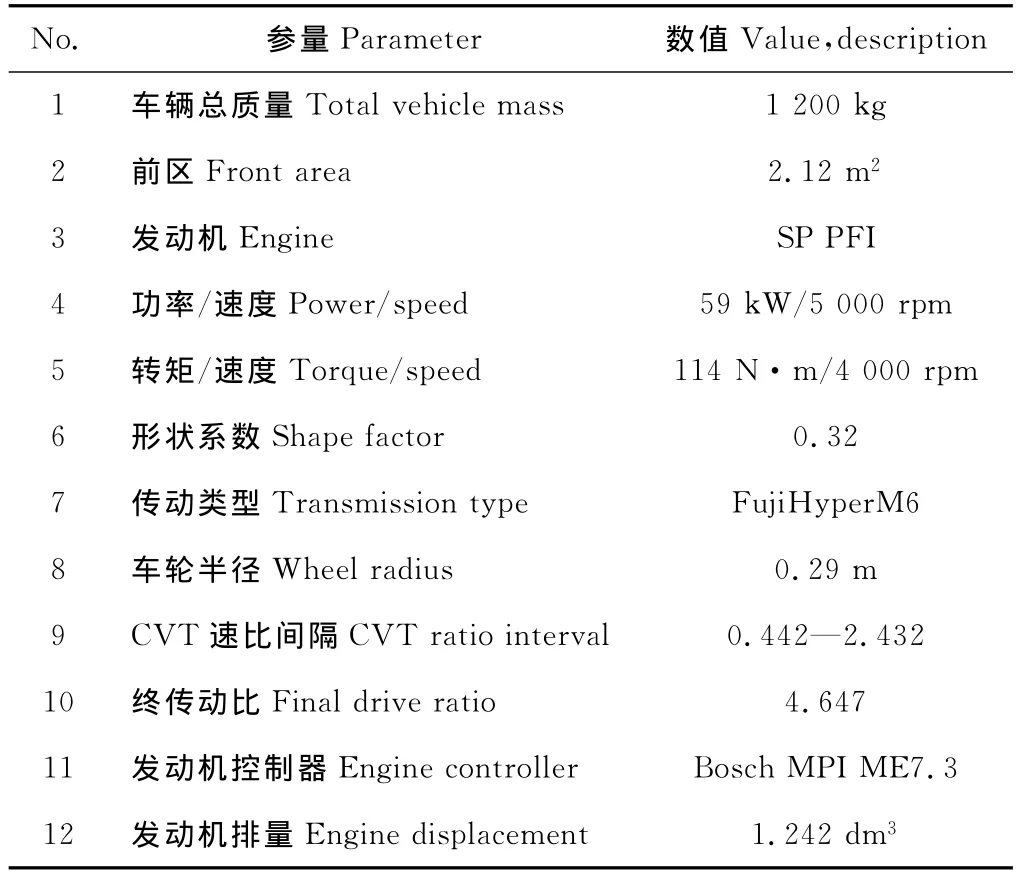
表1 试验轿车的基本参数Table 1 Basic parameters of the examined car

图4指出在加速度过程中，直接关系到采用CVT传动系控制策略。

对于动态策略（D）的情况，用传动系高速比和发动机高转速强烈加速来表示其特征，比较起来相对高于经济策略（E），传动系速比分析造成（图5）可能区分试验过程的两阶段。

在后一阶段该参数值相当小时，用传动系速比快速增大来说明初始阶段的特性，有关初始阶段的详细分析示于图6和7。

在瞬态过程的试验初始阶段，CVT中传动系速比增加，它关系到发动机角速度增加。

在加速度分析阶段，CVT速比增加策略E（图6（a））几乎高于策略E（图7（a））情况三倍。

图中曲线同时还指出，只有在相当大的油门开度（图6和7A段）CVT速比发生快速增加。

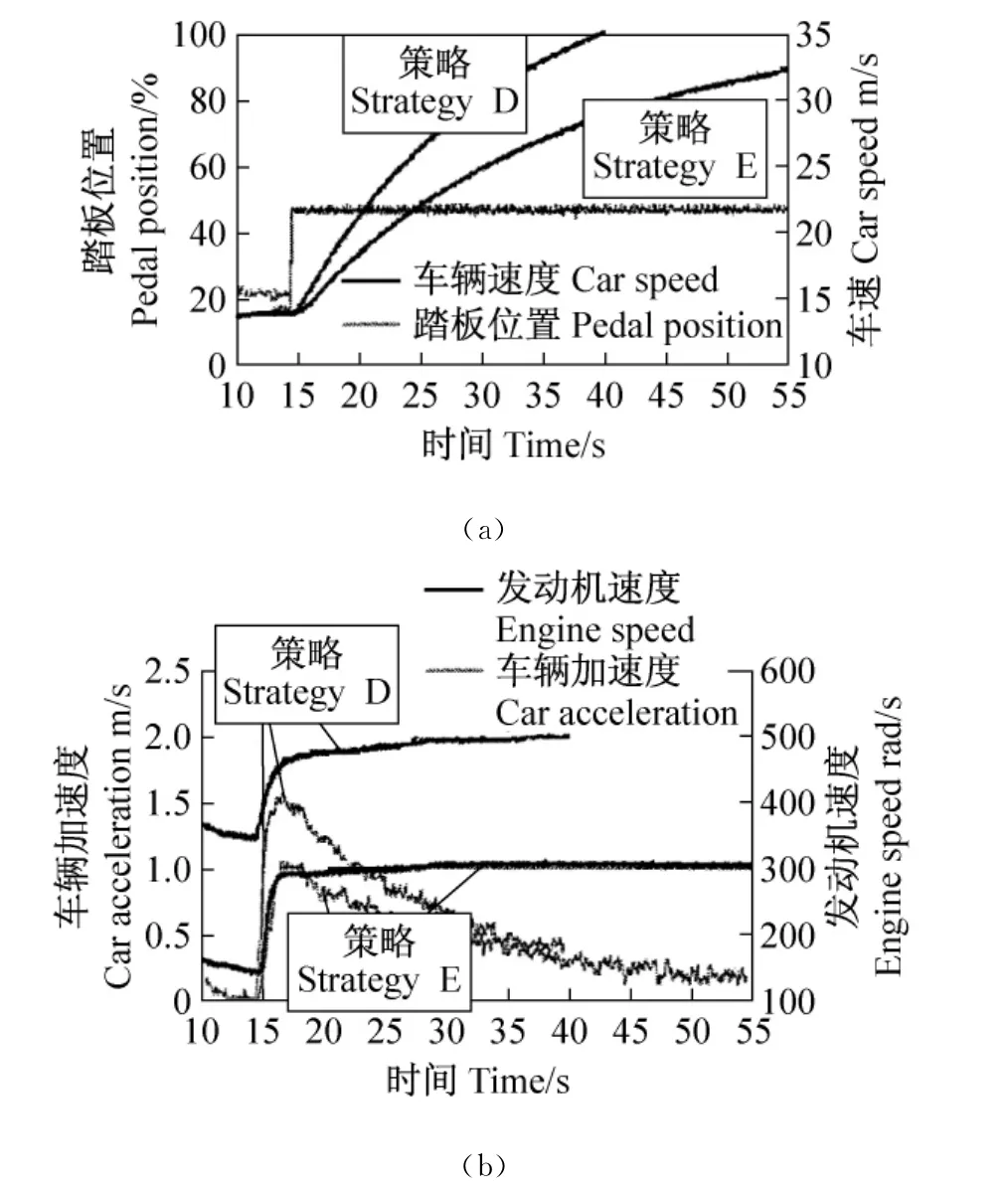
图4 轿车加速试验采用的两种控制策略的比较：（a）输入信号和速度图和（b）轿车加速度和发动机速度Fig.4 Comparison between a test of car acceleration for two control strategies：（a）input signal and velocity profile and（b）car acceleration and engine speed

图5 对于两种控制策略从常速加速时传动系速比Fig.5 Drive train ratio during acceleration from constant speed for two control strategies

这样的一CVT中的换档速度曲线，结果为瞬时和要求传动系速比不同，这种CVT的滞后响应，导致一不良的轿车瞬时加速度。这样加速度快速增加超过初始阶段（J），它包含点A和B曲线段。点B关系到在发动机曲轴相当大角加速度影响高的换档速度发生（图8），它导致在轿车车轮上的驱动力减少，按下式计算：

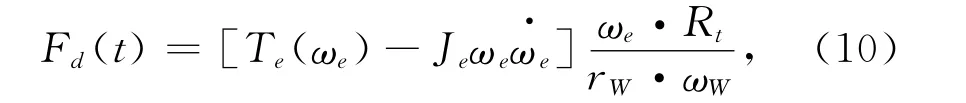
式中Rf：终传动比，

rW：驱动车轮半径。

特别对于策略E情况（图6（b）），它表示一小转矩剩余，在曲线转角表明有明显的汽车加速度。

图6 瞬态过程的初始阶段—策略E：（a）控制过程数值特性和（b）发动机速度和车辆线性加速度Fig.6 Initial phase of the transient process—strategy E：（a）values specific for the control process and（b）engine speed and linear car acceleration

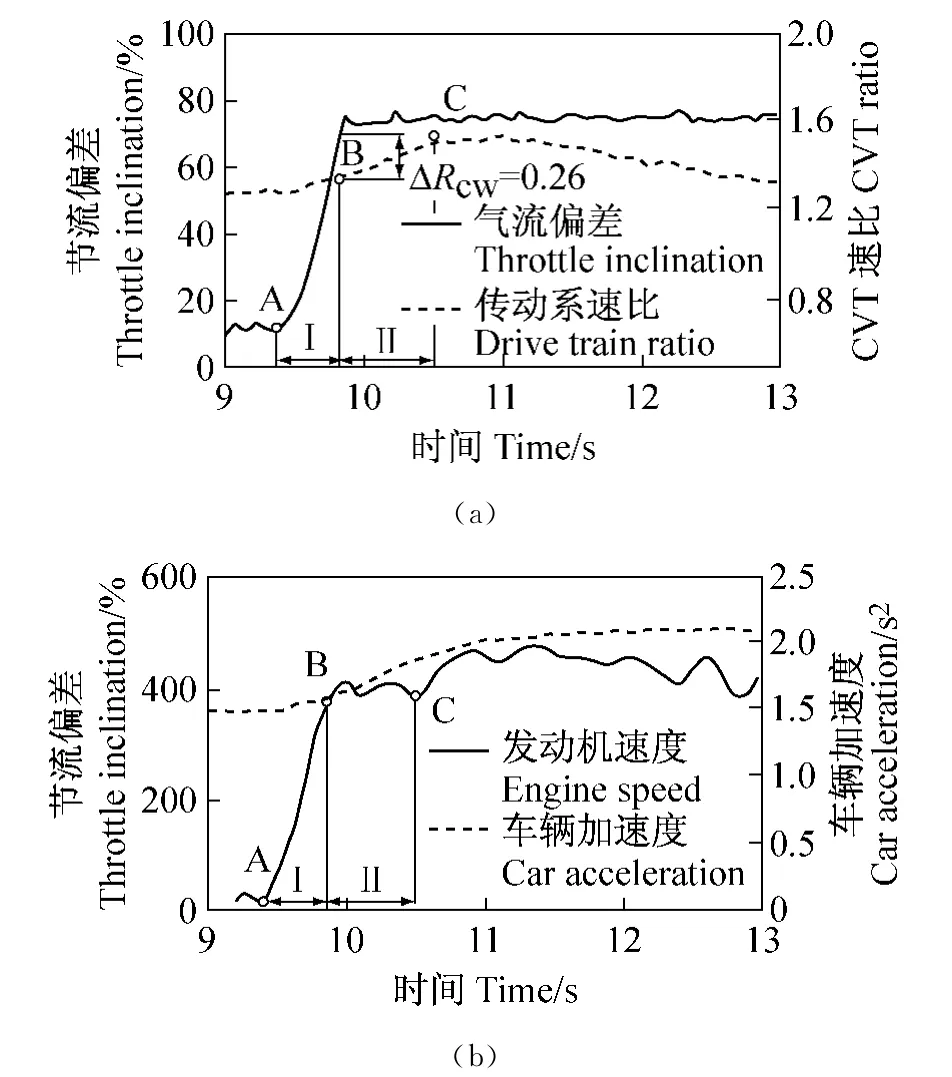
图7 车辆加速度瞬态过程初始阶段—策略D：（a）控制过程数值特性和（b）发动机速度和轿车线性加速度Fig.7 Initial phase of the transient phase of car acceleration—strategy D：（a）values specific for the control process and（b）engine speed and linear car acceleration

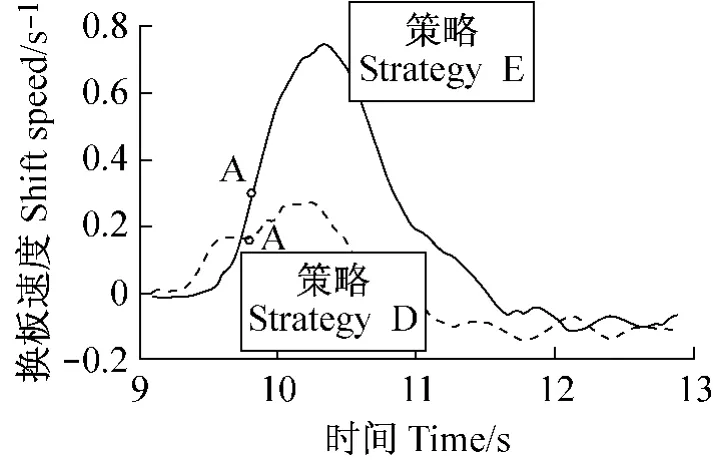
图8 两控制策略换档速度间比较Fig.8 Comparison between the shift speed for two control strategies

C点表示在传动系速比增加阶段的末端，该加速度曲线达到最大值。

对于策略D在车辆加速度曲线内，可以监测到相同的关系（图7（b））。在这种情况，发动机转矩大的剩余和较小的换档速度导致一更有规律的曲线。

5 结论

传统的CVT算法不能保证在瞬态过程正确的驱动力，这是由于动力系速比快速增大的结果。控制系统和换档速度关系滞后发生造成控制误差，导致产生不规则的驱动力。本文指出依据于换档速度，在汽车很快加速过程中，对发动机转矩剩余可具有有利的影响。（章钦迟译自Int.J.Vehicle Design，Vol.54No.1 2010）

［1］Akehurst，S.，Vaughan，N.and Simner，D.（1999）‘An investigation into the loss mechanisms associated with an automotive metal－belt CVT’，European Automotive Congress Vehicle Systems Technology for the Next Century，STA991407，Barcelona

［2］Boos，M.and Vorndran，R.（1994）The ZF CFT 20E Continuously－Variable Transmission for Mid－Range Automobiles，SAE Paper Nr 945028，Detroit，Michigan，USA.

［3］Förster，H.J.（1991）Entwicklungsreserven des Verbrennungsmotors zur Schonung von Energie und Umwelt－Teil 1，Automobiltechnische Zeitschrift Nr.5，pp.SS258－SS570.

［4］Fujii，T.and Kanehara，S.（1993）A Study of a Metal Pushing V－Belt Type CVT－Part 1：Relation between Transmitted Torque and Pulley Thrust，ASE Paper 930666，p.8.

［5］Holloway，D.（1999）Efficiency of the Subaru Justy’s E－lectronic Continuously Variable Transmission and Final Drive，University of Maryland’s Mechanical Engineering Department，p.10.

［6］Ide，T.（2000）Effect of Belt Loss and Oil Pump Loss on the Fuel Economy of a Vehicle with a Metal V－Belt CVT，Seoul 2000FISITA World Automotive Congress，F2000A131，p.6.

［7］Jantos，J.（2001）Control of the Drivetrain Ratio Derivative in Passenger Car Powertrain with CVT，SAE Tech－nical Paper Series，SAE 2001World Congress，Detroit，Michigan，Nr 2001－01－1159，p.6，SAE Transactions，Journal of Passenger Cars－Mechanical Systems，SAE 2001，pp.1277－1284.

［8］Kim，H.and Lee，J.（1994）‘Analysis of belt behavior and slip characteristics for a metal V－belt CVT’，Mechanism and Machine Theory，Vol.29，No.6，pp.865－876.

［9］Koch，L.and Zeller，P.（1987）Prüfstand für dynamische Untersuchungen an Verbrennungsmotoren，Automobiltechnische Zeitschrift No.11，pp.SS585－SS592.