发射率影响修正近似公式及其适用性分析*

原遵东陈桂生

（1.中国计量科学研究院，北京100013；2.中国测试技术研究院，成都610021）

发射率影响修正近似公式及其适用性分析*

原遵东1陈桂生2

（1.中国计量科学研究院，北京100013；2.中国测试技术研究院，成都610021）

黑体辐射源的有效发射率影响是辐射测温计量标准中的重要影响因素。本文利用有效亮度温度概念，对辐射温度计或黑体辐射源检定校准中的发射率影响修正模型的多种简化形式进行了分析比较。定量分析了Wien近似、忽略环境辐射近似和微差近似等几种近似模型的温度与波长适用性。其中微差模型具有简明的物理含义，经典的短波高温修正模型不宜用于常见的8～14μm辐射温度计的测量结果修正。在有效亮度温度测量与校准的发射率修正和不确定度传播计算中，本文分析结果为在不同波长和温度范围合理选择简化公式提供了参考依据。

发射率修正；有效亮度温度；适用性；辐射温度计；黑体辐射源；校准；不确定度

0 引言

辐射测温的直接结果是以理想黑体特性表示的表观温度。发射率影响修正是辐射测温获得真实温度的关键，在温标复现、辐射温度计和黑体辐射源的检定校准中也是必须考虑的因素［1，2］。由于辐射测温已从早期的短波高温测量扩展到可利用中长红外测量室温乃至更低温度，经典的基于Wien公式和忽略环境辐射的短波高温测量的发射率修正模型常被沿用到红外中低温测量范围的修正和不确定度评定。在用辐射温度计规程［3－5］均不修正黑体辐射源（简称辐射源）发射率偏离1对检定结果的影响。不确定度分析表明，规程对辐射源发射率的要求对于1%级8～14μm辐射温度计的检定远不够理想。例如在1000℃，0.995的发射率对8～14μm温度计检定结果的影响为3.7℃［6］。因此，辐射源发射率影响修正及其不确定度评定是检定校准（简称校准）方法中的关键技术之一。

针对辐射温度计校准，本文利用有效亮度温度概念，得到发射率修正模型，重点对几种近似公式的适用性进行了定性和定量分析比较。

1 有效亮度温度

辐射测温的理论基础是Planck黑体辐射定律：

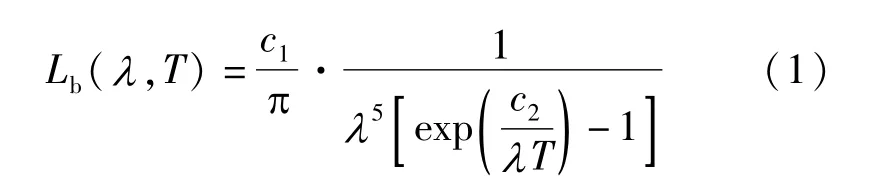
式中：Lb（λ，T）为黑体在波长λ和温度T的光谱辐射亮度；c1为第一辐射常数；第二辐射常数c2＝0.014388m·K。

经典亮度温度的概念广泛用于高温测量，其定义为热辐射体与黑体在同一波长的光谱辐射亮度相等时的黑体温度。以下用校准中常用的辐射源作为讨论的热辐射体的具体对象，则：

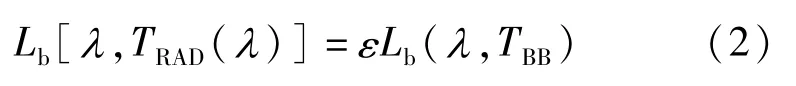
式中：TRAD为辐射源在波长λ下的（经典）亮度温度；TBB为辐射源实际温度；ε为辐射源发射率。

红外亮度测温法从高温下延到常温附近，温度计测量的辐射不仅包括被测目标发出的热辐射，也包含反射的环境辐射影响。后者对测量结果的影响很大，不能忽略。在经典理论中，反射的环境辐射是一种始终伴随着中低温亮度测温法的误差因素，这种情形下的亮度温度测量结果是包含了反射误差的亮度温度。

有效亮度温度定义为热辐射体的有效光谱辐射亮度与黑体的光谱辐射亮度相等时的黑体温度［7，8］。它反映了亮度测温法的实际测量结果，是在存在环境辐射的测量条件下经典亮度温度测量仪表的实际测量结果，是对经典亮度温度的扩展。检定校准环境条件通常可近似为在均匀环境温度条件的封闭大环境，可将环境亮度视为环境温度下的黑体辐射亮度，则：

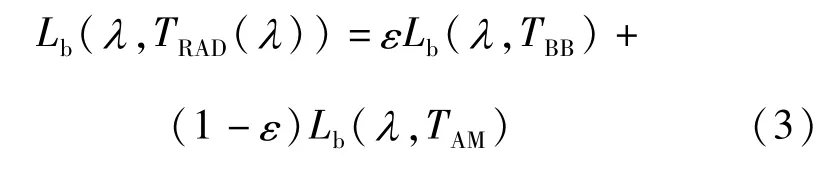
式中：TAM为环境温度。

在不存在环境辐射的条件下，有效亮度温度等于经典亮度温度。以下将有效亮度温度简称亮度温度。

辐射源在波长λ的亮度温度为：

2 亮度温度偏离实际温度的程度

经典亮度温度理论，分别修正发射率对经典亮度温度的影响和环境辐射反射引起的经典亮度温度的误差［9，2］。依据有效亮度温度的概念，利用式（5）可直接计算亮度温度偏离实际温度的程度：

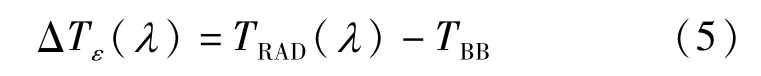
在辐射温度计检定的典型条件——环境温度20℃、发射率0.995下，基于式（4）和（5）的计算结果见表1。由于8～14μm宽带辐射温度计的极限有效波长（亦称极限等效波长）［10］接近10μm，表中10μm的数据也近似表示8～14μm辐射温度计示值受发射率的影响值。

3 简化的近似公式及其适用性

简化公式可方便计算，有时能更直观简明地体现物理意义，便于定性理解。在检定校准中采用简单而又足够准确的近似公式是有意义的，特别是用于不确定度分析与计算。但前提是定量了解其适用条件和近似引起的误差是必要的。

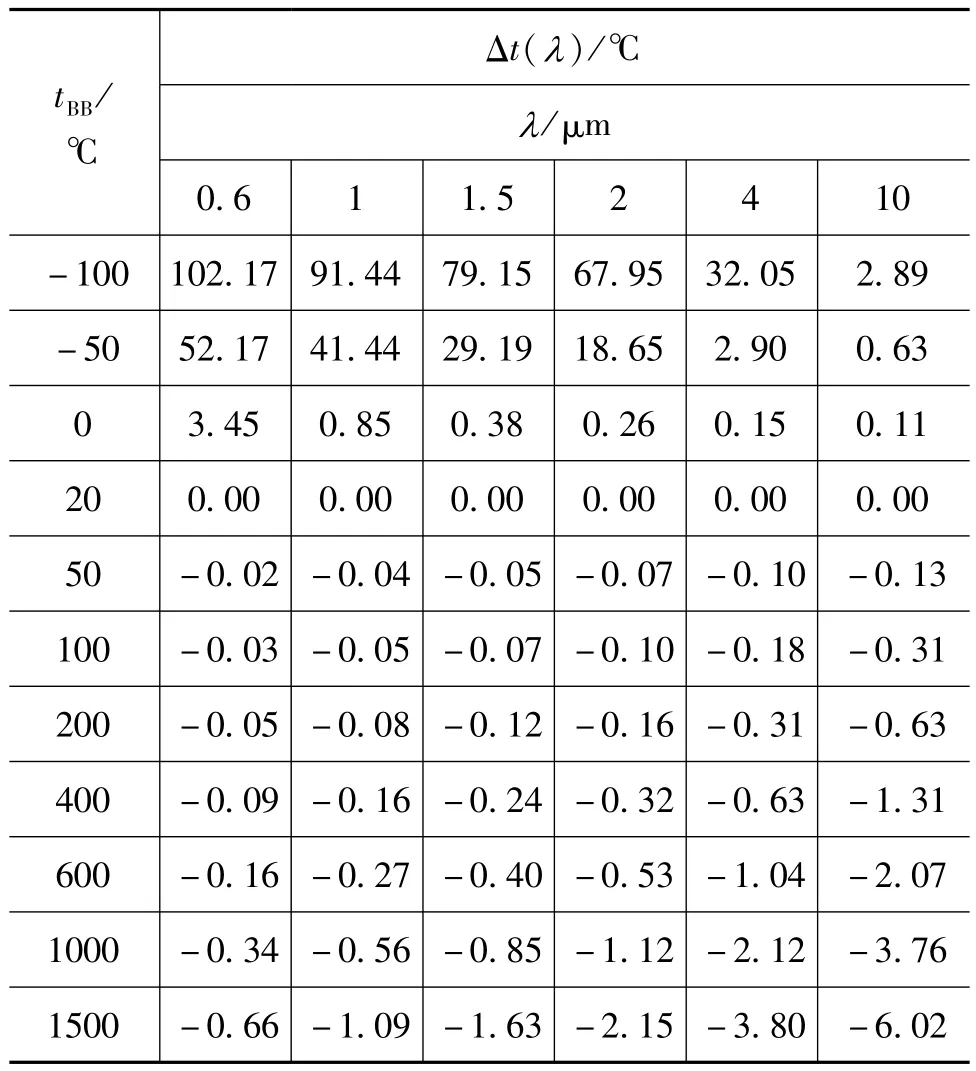
表1 环境温度为20℃时辐射源发射率0.995的影响

表2列出的式（6）至（8）分别为式（5）的3种近似模型公式——Wien近似、忽略环境辐射近似和上述双重近似公式。微差形式一列给出与左侧公式对应的微差形式，公式编号相应地加字母a，适用于高发射率场合。

式（5）的直接微差形式远比式（5）复杂，失去实用意义；式（5a）为以TBB近似替代TRAD后得到的近似公式，由于推导中的近似处理的缘故，在－50℃以下低温和短波时误差急剧增大，但对常规测温范围没有不可忽略的影响。此微差近似的10%误差临界线见图1最左侧虚线。式（5a）右侧为三项因子形式，依次为式（8a）等号的右侧项（与波长、温度的平方和发射率偏离1的程度成正比）、Planck修正项和环境辐射修正项（环境温度下为0，大于环境温度时大于0，小于时小于0）。此微差公式的突出优点是物理含义明显、易于理解与记忆，而近似引起的不适用性很有限。式（6a）至（8a）为忽略相应修正项的结果。

以下在环境温度20℃、发射率0.995条件下，以模型近似公式与准确的式（5）之比反映模型近似公式的准确程度，以微差公式与表2左侧公式之比反映微差近似的准确程度。表2在模型近似公式下方列出各公式的典型波长下的适用温度范围，在微差公式下方列出微差公式相对于左侧公式的一致程度。

表2 公式比较与适用范围

对式（5）分别采用Wien近似、忽略环境辐射近似的误差临界线见图1，临界误差绝对值为1%和10%。临界线的下方为近似方法的适用范围。对于常规水平的校准中的发射率修正，可以采用误差在10%以内为公式适用范围，对于辐射源校准可以采用误差在1%以内为适用范围。Wien与忽略环境辐射双重近似的适用范围为两种近似适用范围的交集（临界线下方的共同区域）。

测温点趋近环境温度，相对误差幅度急剧增大；测温点低于环境温度时，误差幅度随温度降低迅速增大，因为这时的环境已处于相对高温。忽略环境辐射误差临界线表明，对于短波温度计，由于测温下限温度较高，不能忽略环境辐射影响的温度范围常低于测温下限，不影响常规的实际测温，这一点与常识一致。

在常规测温范围，表2中的各微差公式与其左侧公式等价。

式（8a）是以往文献和教科书中广泛采用的修正模型，但随着红外测温范围的下延，常被用于短波高温测量之外的范围。表3列出式（8a）与准确的式（5）之比表示式（8a）的适用性（比值越接近1越准确）。表中的斜体数据是因为忽略环境辐射引起的误差超过1%的区域，下划线数据是采用Wien近似引起的误差超过1%的区域。对于如8～14μm温度计这样的长波辐射温度计，既忽略环境辐射（要求TBB≫TAM）又采用Wien近似（要求λTBB≪c2）使得式（8a）对所有温度范围都不适用。其具体原因为，Wien近似将式（5a）右侧的第2个因子近似为1，是导致表3中低温端比值偏离1的主因；忽略环境辐射将第3个因子近似为1，是导致高温和长波端比值大于1的主因。

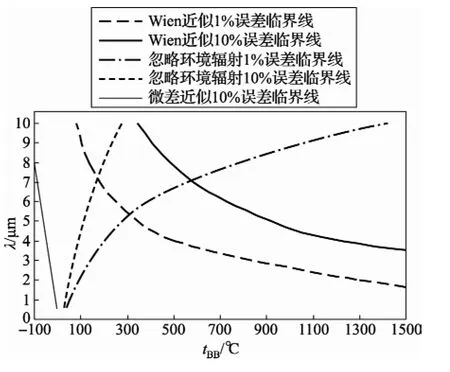
图1 Wien近似和忽略环境辐射的1%和10%误差临界线

表3 环境温度20℃辐射源发射率0.995时不同温度与波长下式（8a）与式（5）的比值

4 总结

对采用有效亮度温度概念得到辐射源发射率影响计算公式，它包含了经典理论中的发射率影响和环境辐射影响两部分。对多种近似模型公式进行了适用性定量分析，包括忽略环境辐射、Wien近似和同时包含上述两者的模型近似，并与它们的微差近似进行了比较。

有效亮度温度的发射率影响公式（式4）适用于各种波长下的所有温度。本文得到的其微差形式公式（式5a至8a）具有直观的物理意义，易于理解，便于定性分析。经典的高温修正近似公式（8）和（8a）只适用于短波测量，对于广泛应用的8～14μm辐射温度计的修正和不确定度评定都不适用。

本文推导结果和定性定量分析结论可作为辐射温度计和辐射源校准中发射率修正计算与不确定度评定的公式选择的参考依据。

［1］JFischer，M Battuello，M Sadli，M Ballico，SN Park，P Saunders，Z Yuan，B C Johnson，E van der Ham，F Sakuma，GMachin，N Fox，W Li，S Ugur，M Matveyev.Uncertainty Budgets for Realization of ITS－90 by Radiation Thermometry［C］，Temperature：ItsMeasurement and Control in Science and Industry，vol.7，New York，2003：631－638

［2］P Saunders，J Fischer，M Sadli，M Battuello，CW Park，Z Yuan，H Yoon，W Li，E van der Ham，F Sakuma，J Ishii，M Ballico，G Machin，N Fox，J Hollandt，M Matveyev，P Bloembergen，S Ugur.Uncertainty Budgets for Calibration of Radiation Thermometers below the Silver Point［J］.Int J Thermophys.2008，29（3）：1066－1083

［3］JJG 856—1994 500℃以下工作用辐射温度计［S］，1994

［4］JJG 415—2001工作用辐射温度计［S］，2001

［5］JJG 67—2003，工作用全辐射温度计［S］，2003

［6］原遵东.黑体辐射源发射率对辐射测温准确度的影响及修正方法［J］.计量学报，2007，28（3A）：19－22

［7］原遵东.有效亮度温度理论［J］.计量学报，2009，30（6）：493－497

［8］Z Yuan.Effective Radiance Temperature：Concept，Measurementand Effective Wavelength［C］.ITS9 Symposium（USA），2012

［9］P Saunders.Radiation Thermometry：Fundamentals and Applications in the Petrochemical Industry.SPIE Press，Bellingham，Washington，2007

［10］原遵东.辐射温度计的等效波长及其应用［J］.仪器仪表学报，2009，30（2）：374－379

10.3969／j.issn.1000－0771.2013.4.02

质检公益性行业科研专项资助项目（200910106）