用水平仪测量竖直轴线铅垂度的误差分析

尹小恰 任顺清 陶子英

（哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨150001）

用水平仪测量竖直轴线铅垂度的误差分析

尹小恰 任顺清 陶子英

（哈尔滨工业大学空间控制与惯性技术研究中心，哈尔滨150001）

针对用水平仪测量竖直轴线对水平面的垂直度的方法，建立一系列坐标系，用方向余弦阵进行传递推导了与水平仪固联坐标系相对于地理坐标系的姿态关系，从而得出水平仪读数与垂直度误差、倾角回转误差和角位置等的关系，由此采用最小二乘法计算了非整周回转轴系的回转轴线的铅直度误差。然后，对于不同的误差源，包括回转误差、水平仪误差、角位置误差，以及测试数据量、轴系回转范围等因素进行了相应的误差分析。

垂直度；水平仪；最小二乘法；误差分析

0 引言

利用水平仪测量整周回转竖直轴系的倾角回转误差，调整其竖直轴线的铅垂度是一种非常成熟的方法［1］，但有的设备，比如六自由度的交会对接仿真测试设备，它上面的三轴转台都是非整周360°的回转，有的回转范围仅有±25°，而且要求其竖直的外环轴轴线与竖直移动导轨平行。文献［2］论述了用经纬仪测量竖直导轨对水平面的垂直度方法，如果用水平仪测量三轴转台的外环轴轴线对水平面的垂直度，则可以测量它们之间的平行度误差。本文对如何测量旋转轴的垂直度提出了一种新的非整周测量方法，使水平仪可以测量非整周回转轴系的轴线铅垂度，并对非整周测量方法的误差源和测量精度进行了研究。

1 测试原理与数据处理方法

1.1 测试原理

以立式单轴转台为例，阐述水平仪测试竖直轴线铅垂度的基本原理，建立如下坐标系：

地理坐标系 o0x0y0z0是固联在地基上的坐标系，如图1所示，o0x0在水平面内，o0z0向上与重力加速度矢量平行，o0y0水平并由右手定则确定。

轴套坐标系 o1x1y1z1是固联在轴套上的坐标系，如图1所示，o1z1与主轴的回转轴线一致。主轴回转轴线对水平面的垂直度为Δθ0，它可认为是在地理坐标系o0x0y0z0的基础上绕o0x0轴旋转Δθx0，再绕o0y0轴旋转Δθy0形成。轴套坐标系相对地理坐标系的姿态矩阵为

图1 基准坐标系与轴套坐标系

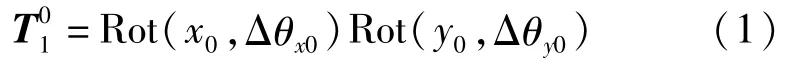
注：Rot（i，θ）表示绕i轴旋转θ角形成的新的坐标系相对于原坐标系的方向余弦阵。

主轴坐标系 o2x2y2z2是固联在主轴上的旋转坐标系，如图2所示，它的o2z2轴与主轴轴线一致，它的初始位置与o1x1y1z1一致，该坐标系是在考虑主轴的倾角回转误差Δθx1（γ）、Δθy1（γ）的基础上绕o1z1轴旋转γ角形成的。主轴坐标系相对轴套坐标系的姿态矩阵为

安装基面坐标系 o3x3y3z3也是固联在主轴上的坐标系，如图3所示，它是考虑水平仪安装基面相对于轴系轴线的垂直度Δαx2、Δαy2形成的。安装基面坐标系相对主轴坐标系的姿态矩阵为

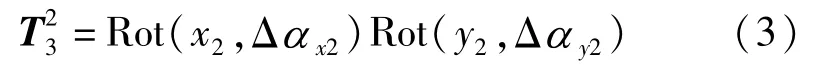
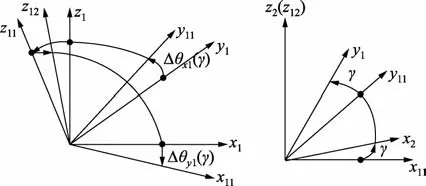
图2 主轴坐标系

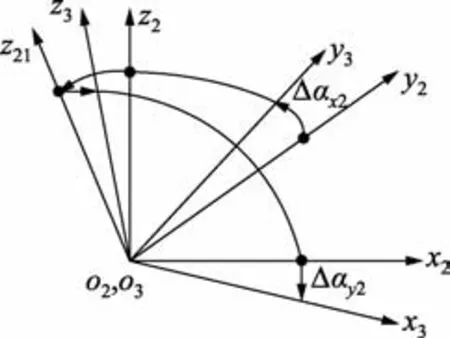
图3 安装基面坐标系

利用坐标系之间姿态的传递关系和式（1）～（3），安装基面坐标系相对于地理坐标系的姿态矩阵为

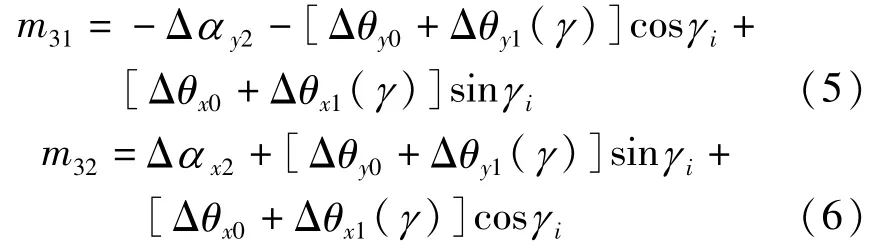
目前的机械加工水平，其回转误差小于1″或者更低，可以忽略回转误差项Δθx1（γ）、Δθy1（γ），式（5）、（6）可以简化为

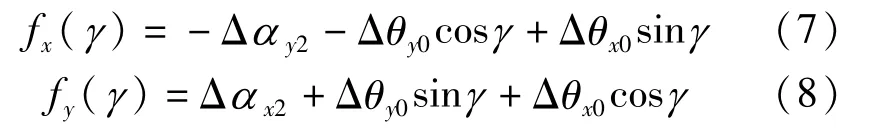
根据式（7）或（8），可以只用一个水平仪使其置于x或y方向便可测试出二维铅垂度Δθx0、Δθy0。Δαx2、Δαy2包含了台面对回转轴线的垂直度以及水平仪本身的零位误差，表现为均值项，在铅垂度调整时，调整地脚使水平仪读数在任何位置都接近这个常数项，则铅垂度Δθx0、Δθy0将逐渐接近于零。

1.2 数据处理方法

在用水平仪测试垂直度时，以o3x3上水平仪测量为例（o3y3上同理），如图4所示，将水平仪置于x方向。设回转范围等间隔取n点读取水平仪数据，如果竖直轴系处于不同角位置γi，i＝0，1，2，…，n－1，n为测试点数，水平仪的量测数据为fx（γi），由式（7），可以辨识出水平仪读数的常数项Δαy2（包括水平仪零位误差及台面对轴线的垂直度误差）、二维铅垂度Δθx0、Δθy0：

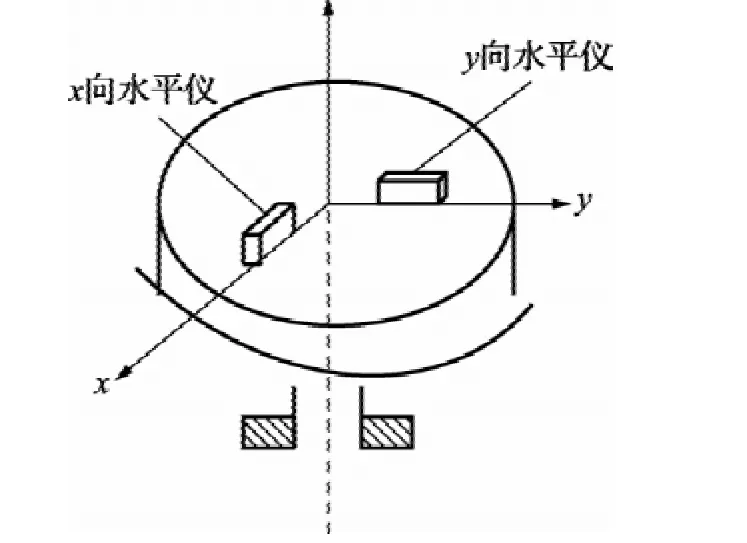
图4 水平仪位置

在对垂直度误差做精度分析时，残差向量记为ξ。由式（7）可写出矩阵形式

根据最小二乘法原理得

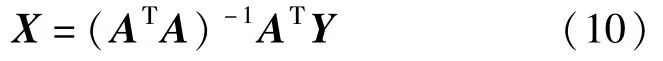
由此可处理出竖直轴线铅垂度大小为

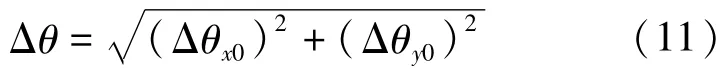
或同理可将水平仪置于如图4中y方向，根据式（8）处理出竖直轴线铅垂度大小。

2 误差分析

2.1 辨识系数的误差分析

对于式（10）中，令B＝（AΤA）－1AΤ

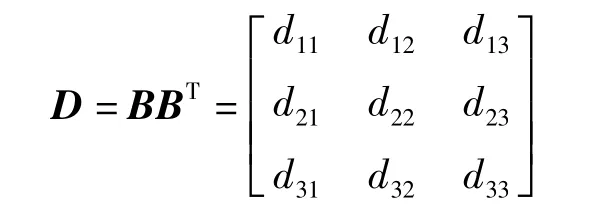
水平仪的测试不确定度是σ0，则Δαy2、Δθy0、Δθx0的不确定度分别为

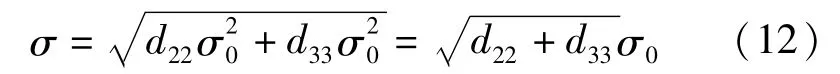
2.2 测试实例

实际测量的水平仪测试不确定度σ0＝0.2″。当测试区间为整周360°、180°、90°、45°时，分别测量并计算铅垂度及测量不确定度；当测试区间一定，改变角度间隔，分别测量并计算铅垂度及测量精度。测量计算结果如表1所示。为测试的常数项，它的来源包括两部分，水平仪的底面与轴线的垂直度，还有水平仪的零位误差，如果铅垂度较大并需要调整时，可以调整转台地脚或相应的调整机构，使水平仪在转动范围内均接近这个常数项，所以这个常数项的辨识精度决定了轴线铅垂度的调整精度。则水平仪测数值轴系铅垂度的测试精度可表示为

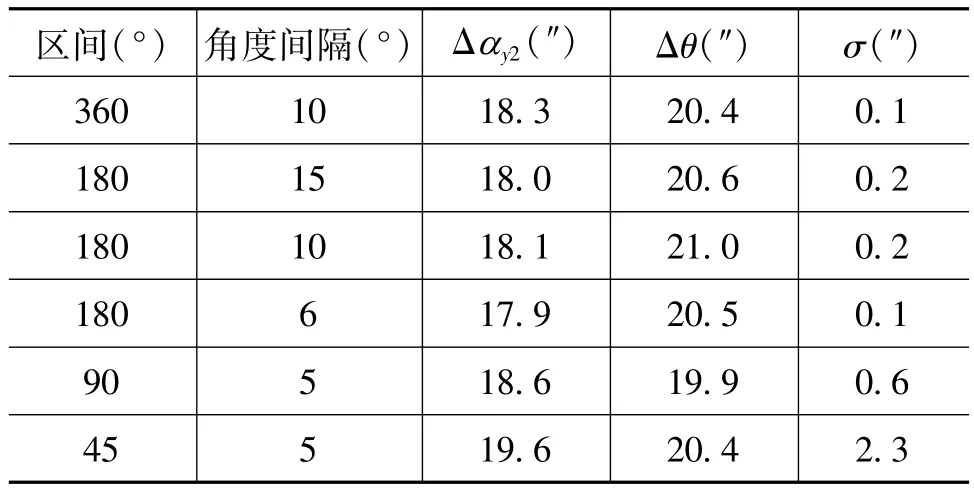
表1 实际测量的计算结果一览表

可见对于非整周回转轴系，用水平仪同样可以测量其铅垂度的大小。但随着轴系回转范围的减小，测量精度将越来越低。

3 测试误差源分析

影响铅垂度测试精度的因素有：数据处理方法的精度、水平仪的测量不确定度、轴系回转误差、角位置误差、测量点数和测角范围等。

3.1 水平仪测量不确定度

由式（12）可知，水平仪的测试不确定度直接影响测试精度，水平仪测量精度越高，测试结果精度就越高。

由于2.2测试实例中整周与非整周测量时水平仪测试精度都是σ0＝0.2″，故此实例中可以认为水平仪测量不确定度不是影响非整周测试铅垂度的原因。

3.2 轴系回转误差

在第1.1节中，由式（5）、（6）得出式（7）、（8）时，忽略了回转误差项，一定会对测试精度造成影响［3］，假设回转误差Δα的范围为－1″～＋1″，式（7）、（8）转换为

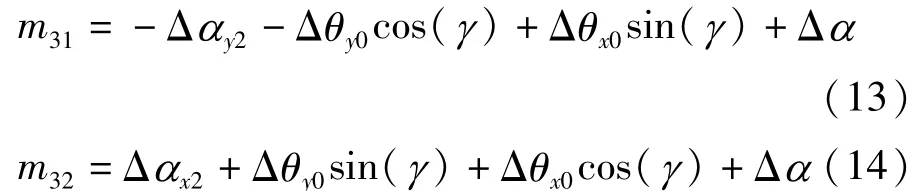
根据回转误差的理论，回转误差的主要谐波成分为二次及二次以上谐波，这里仅考虑其二、三、四次谐波成分。

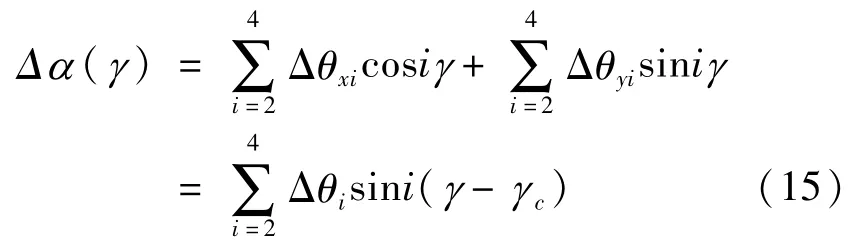
由于测量铅垂度时，往往忽略回转误差，假设回转误差的幅值一般小于1″，当测量铅垂度时往往随机从某个角度开始测试，所以使式（15）中的Δθ2＝0.8″，Δθ3＝0.3″，Δθ4＝0.2″，γc采用在［0，2π）的100个随机数进行统计，用Matlab编程仿真，得出常数项标准差和铅垂度误差测试标准差见表2。

从表2中可以看出，轴系的回转范围越小，倾角回转误差的存在对铅垂度测试误差的影响越大。

3.3 角位置误差

为了分析角位置误差对测试精度的影响，假设角位置误差为Δγ，目前角位置误差调试在±5″已经非常容易做到，式（7）、（8）转换为

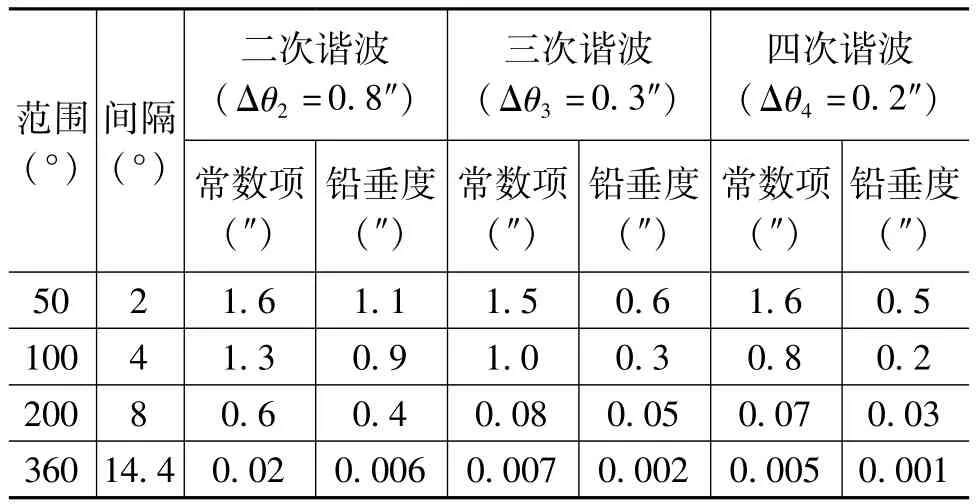
表2 倾角回转误差对于常数项Δαy2与铅垂度Δθ测试的影响的标准差

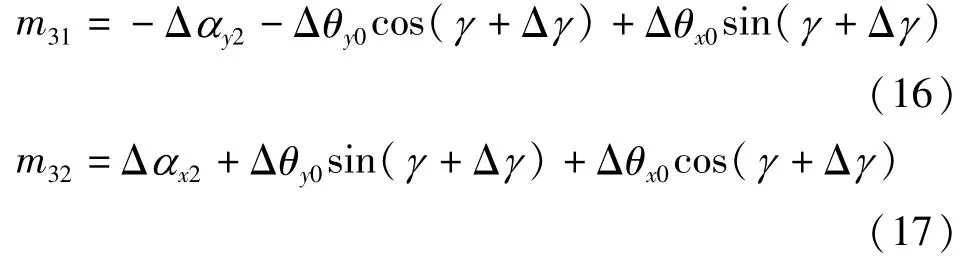
如果Δθx0、Δθy0调整到小于60″，则Δγ对水平仪读数的影响为60″sinΔγ＝0.0015″，远小于水平仪的分辨力。测试铅垂度，采用电控转台时，角位置误差对铅垂度测试的影响可以忽略不计。

假设测角系统没有调整完毕，用刻度盘的刻线进行定位，定位误差很大，分别假设γ有0.1°和0.5°的随机误差。同样采用计算机仿真计算，统计100次所产生的标准差见表3。根据角位置误差的理论，角位置误差的主要谐波成分为一、二次谐波。

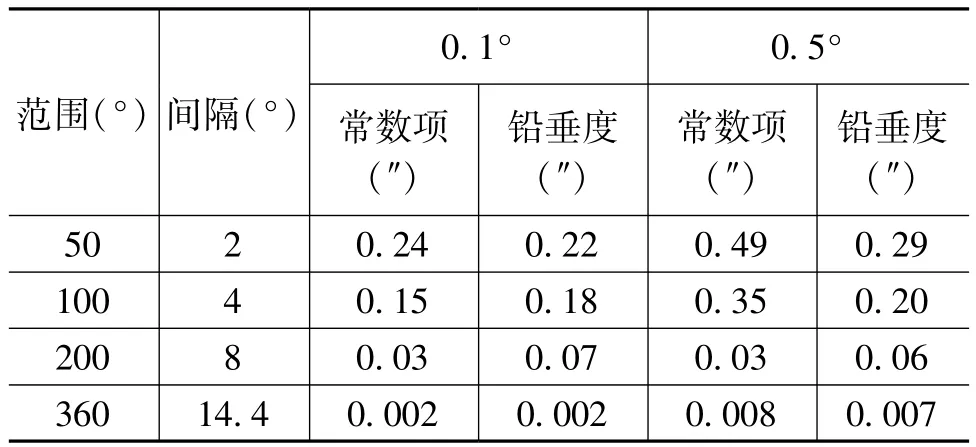
表3 角位置误差对于常数项Δαy2与铅垂度Δθ测试的影响的标准差

从表3中可以看出，轴系的回转范围越小，角位置误差的存在对铅垂度测试误差的影响越大。在50°的回转范围内，测量点数为26点，角位置的随机误差为0.5°时，铅垂度测量误差小于1″，故实际中角位置误差对铅垂度测试误差的影响是极其微小的，尤其在采用电控时完全可以忽略不计。

3.4 测量点数

2.2 节非整周测试中，当测角范围180°不变，测量点数变化时，测试精度也会发生变化。如图5所示。

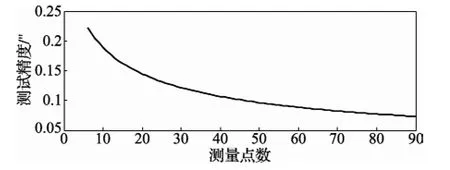
图5 测量点数对精度的影响

由图5可知，随着测量点数越来越多，即角度间隔越来越小，测试精度越来越高。在测角范围180°时，当测量点数为8时，测试精度已可达到0.2″。

3.5 测角范围

由2.2节整周测试与非整周测试的差异可知，测量区间的不同会影响测试精度。步长取5°，当测角范围为45°、46°、…、360°时，根据式（7）、（8），测试精度的变化如图6所示。

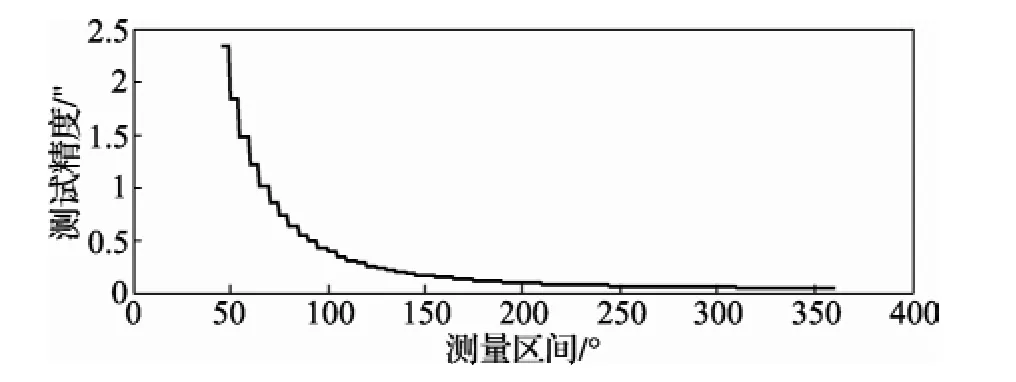
图6 测角区间对精度的影响

由图6可知，当测角范围150°时，测试精度已趋近于整周测试精度，当测角范围65°时，测试精度约达到1″。

3.6 数据处理精度

由1.2中数据处理采用最小二乘法，而最小二乘法本身的误差定会影响铅垂度测试精度，最小二乘法的测量误差一般达10－2数量级［4－5］。

由式（4）～（6）知，在数据处理过程中忽略了二阶小量，这也会对测试结果造成影响，然而由上面对角位置误差影响的分析可知，一阶小量角位置误差的影响尚可忽略不计，二阶小量对测试结果的影响更是微乎其微，可忽略不计。

4 结论

本文分析了用水平仪测试竖直轴线铅垂度的基本原理，给出了非整周回转轴系铅垂度的测试方法与数据处理方法。针对水平仪的误差、回转轴系误差中的各次谐波、角位置误差、测量点数的多少和测角范围的大小等误差源对铅垂度测试误差的影响，采用仿真计算和实测验证的方法进行了分析，结果表明回转误差对测试精度影响较大；当测量范围一定时，若所得测试精度较低，可通过减小角度间隔增加测量点数的方法提高测试精度。本文的分析为正确估计铅垂度，调整多自由度系统中的竖直轴系的初始对准方法、对准精度提供了一定的依据。

［1］任顺清，王俊柱.用水平仪测试倾角回转误差的数据处理［J］.哈尔滨工业大学报，2006（6）：837－839

［2］任顺清，陈海兵，赵洪波.用经纬仪测量大尺寸三维导轨垂直度的方法［J］.仪器仪表学报学报，2012（1）：188－193

［3］贾宏进，秦石乔，胡浩军，张宝东.轴系倾角回转误差与垂直度测量方法［J］.计量技术，2008（11）：25－28

［4］陈显枝，陈冲.基于最小二乘改进算法的时变系统参数辨识［J］.福州大学学报，2005（2）：163－166

［5］宋明顺，顾龙芳，陈意华.最小二乘测量结果不确定度的评定［J］.计量技术，2000（1）：43－45

［6］任顺清，马广程，伊国兴，王常虹.测量角位置误差时自准直仪读数与正多面棱体偏差的符号取定［J］.计量技术，2003（12）：42－45

［7］张立新，黄玉美，高峰，何根良，乔雁龙.回转运动坐标定位精度的检测与误差补偿模型［J］.计量学报，20007（4）：317－320

［8］任顺清，陈希军，裘建军.三轴转台垂直度误差的测试与分离技术［J］.计量技术，2002（5）：6－9

10.3969／j.issn.1000－0771.2013.4.03