幅值波动电力信号谐波分析的HHT－FFT方法

梅 永王柏林

（1.南京信息工程大学电子与信息工程学院，南京210044；2.河海大学能源与电气学院，南京210098）

幅值波动电力信号谐波分析的HHT－FFT方法

梅 永1王柏林2

（1.南京信息工程大学电子与信息工程学院，南京210044；2.河海大学能源与电气学院，南京210098）

针对幅值波动的电力信号，提出一种谐波分析新方法——HHT－FFT方法。首先论证了幅值波动是产生间谐波的主要根源，幅值波动也影响整次谐波的幅值和相位的计算。HHT－FFT方法是“HT提取包络——分离包络——工频信号DFT——包络HHT——包络与工频信号合成”的一个迭代过程。该方法排除了整次谐波频谱泄漏产生的虚假间谐波，因此，整次谐波和间谐波的分析结果都更真实、更精确。

幅值波动；非平稳周期号；HHT－FFT；整次谐波；间谐波

0 引言

电力信号的谐波分析一直用DFT（Discrete Fourier transform）方法［1－6］，但是，DFT方法理论上只适合于平稳周期信号［7－8］，所以，工程界常常反应谐波很难测准，间谐波更难测准。过去，谐波分析的注意力主要在同步误差，实际上，现在新型谐波测量装置的同步误差已小于0.01%（对平稳周期信号2～50次谐波的测量精度已优于0.5级）。在这一新情况下，电力信号的非平稳性上升为主要矛盾。迄今，工程上间谐波的测量仍然沿用整次谐波的方法——离散傅里叶变换（DFT）法，即使不管理论上的严谨性，DFT的频谱泄漏也是致命的——频谱泄漏产生虚假的间谐波使得间谐波无法测准。

由于基于DFT的分析方法在分析非稳态信号方面的局限性，小波变换理论［9－11］作为一种分析非稳态信号的方法在谐波分析中得到研究，也取得一些进展，但是当信号中含有较多或相近频率的谐波和间谐波时，小波变换还存在难以克服的困难。

HHT（Hilbert－Huang Transform）［12－13］可看作小波变换的改进，当信号中含有较多或相近频率的谐波和间谐波时，直接用HHT进行谐波分析同样存在模态混淆问题。

本文力图从间谐波产生的机理出发，探索谐波和间谐波分析的新方法，新方法既保留DFT方法在整体频谱和频率细分上的优势，又解决了DFT不适用非平稳周期信号的难题，新方法定名为“HHTFFT方法”。

1 电力信号的平稳性

为了表达上的严谨，先作如下定义：

1）定义1：对于信号

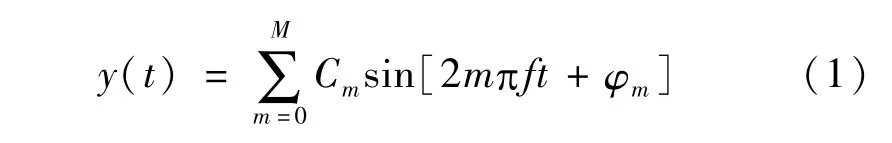
如果幅值Cm、频率f、相位φm都是常数，就称之为平稳周期信号，如果幅值、频率、相位中有一个或多个是时变的，则称之为非平稳周期信号。

必须强调的是：平稳性是针对特定频率而言的，在一个频率上非平稳的信号可能在某个更低的频率上是平稳的。

近年来，在随机信号处理中出了一个新名词叫“周期平稳信号”，以上定义的“平稳周期信号”可看作确定性的“周期平稳信号”。

2）定义2：频率为工频的平稳周期信号特别称为平稳电力信号，频率为工频的非平稳周期信号特别称为非平稳电力信号。

之所以强调“频率为工频”，就是因为平稳性是针对特定频率而言的。电力信号频率和相位的变化比较缓慢和微小，如果同步采样环节的同步误差很小（现在技术上可以做到0.01%），缓慢的频率和相位变化对谐波分析的影响相对较小，而电力信号的幅值波动有时会比较快速和显著，所以，本文主要研究幅值非平稳电力信号的谐波分析方法，频率非平稳和相位非平稳也很值得研究，限于篇幅，本文不展开讨论。

2 幅值非平稳电力信号

我们把幅值非平稳电力信号描述为：

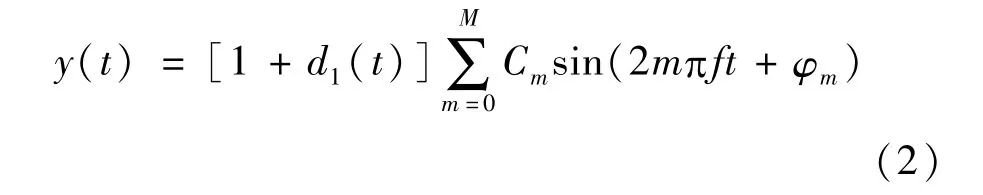
其中，d1（t）是电力信号幅值的波动量，称为包络。在电力系统中包络d1（t）也可能是平稳周期信号或非平稳周期信号。

电力信号的幅值非平稳对谐波分析会带来两大影响：1）产生间谐波；2）导致整次谐波的幅值和相角变化。根据电力信号平稳性定义1、定义2和幅值非平稳电力信号的分析可以得出如下4个结论。

1）结论1：平稳电力信号一定不含间谐波，含间谐波的电力信号一定不是平稳电力信号，间谐波信息主要包含在电力信号的包络之中［17］。

这个结论直接来源于周期信号的傅立叶级数，平稳电力信号y（t）一定可以展开为式（1）所示的傅立叶级数，只要f是工频，式（1）中就只含工频的整数倍频率——整次谐波，不含间谐波。

考虑幅值非平稳中最简单的情况：d1（t）是平稳周期信号，这时d1（t）可描述为：

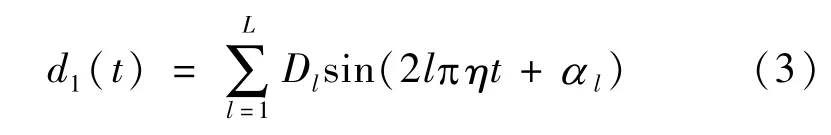
其中，常数Dl和αl分别为d1（t）的第l次谐波的幅值和初相角；η为d1（t）的基波频率；L是d1（t）所含整次谐波的最高次数。将式（3）代入式（2）得：

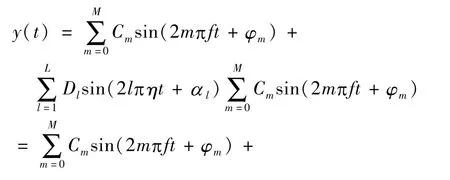
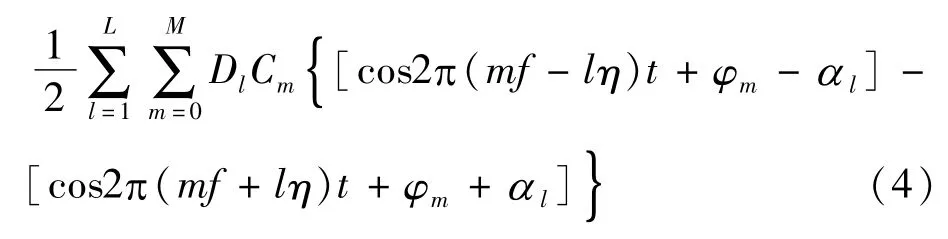
2）结论2：式（2）描述的含包络d1（t）的非平稳电力信号比式（1）描述的平稳电力信号增加了间谐波成份，如果d1（t）是平稳周期信号，那么电力信号式（2）的所有整次谐波和间谐波频点为

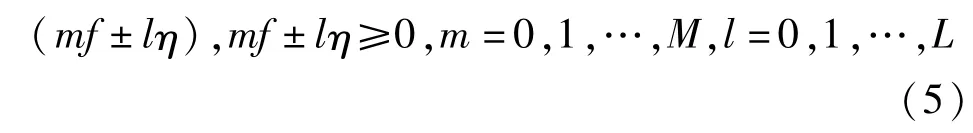
3）结论3：对于式（2）和所描述的非平稳电力信号y（t），如果Lη＜f或y（t）的基波频率f不是d1（t）基波频率η的整数倍，那么包络d1（t）不影响电力信号y（t）的整次谐波（幅值、相位），只包含间谐波。

注意：如果Lη＜f，间谐波的计算就变得更为简单：任一次间谐波只出现在式（4）的一项之中。

4）结论4：对于式（2）所描述的非平稳电力信号y（t），如果Lη≥f且f是η的R倍（R为正整数），则式（5）的频点中

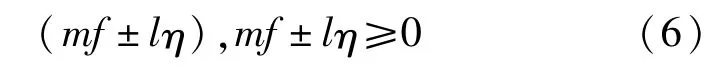
m＝0，1，…，M，l＝R，2R，…，PR，为整次谐波频点，其它为间谐波频点。其中，P＝In t（L／R），In t（.）是将（.）中的数取整。这个结论说明：包络的出现不仅包含间谐波，还会改变整次谐波的幅值和相位。

如果包络d1（t）也是非平稳周期信号，d1（t）可描述为：

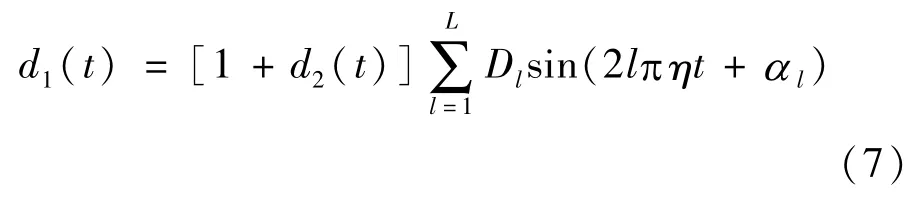
其中，d2（t）为第2层包络。如果d2（t）是平稳周期信号，则d2（t）可描述为

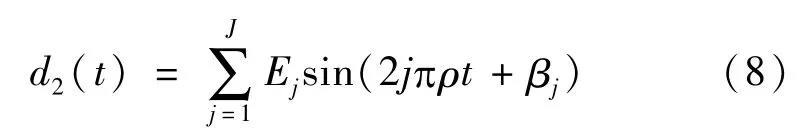
式中，常数Ej和βj分别为d2（t）的第j次谐波的幅值和相位，ρ为d2（t）的基波频率，J是d2（t）所含整次谐波的最高次数。

如果第2层包络d2（t）是非平稳周期信号，可按上述方法从第2层包络d2（t）中再提取出第3层包络d3（t），…，直到第K层包络dK（t）可当作平稳周期信号为止——我们把K称为幅值非平稳电力信号包络的层数，包络层数越多信号的非平稳性越严重。

3 HT－FFT算法

根据上节结论3、4，要准确测量谐波和间谐波，最好的方法是提取出包络，并将包络从信号中逐层剥离。为了叙说简便，先考虑包络层数为一层的情况。首先，对电力信号y（t）连续采样S个周波，得到N点采样序列｛y（n）｝，采样的同步误差应尽量小（按IEC－4－7要求小于0.03%）。

然后，从采样序列｛y（n）｝中提取包络d1（n），提取可以用滤波器、小波分析、局域均值分解和希尔伯特变换等有效方法。

有了包络d1（n），就可以将包络从｛y（n）｝中剥离，剥离方法是

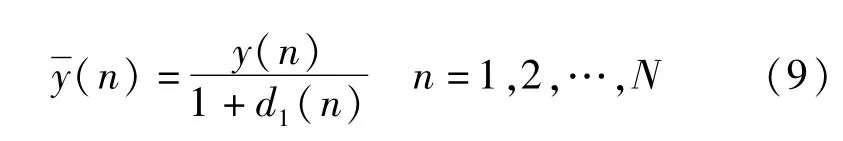
下一步是对包络｛d1（n）｝按频率分解，当｛d1（n）｝为平稳周期信号时可以用DFT或加窗DFT得到d1、d2、…、dL。

最后用式（4）就可以求出各次整次谐波、间谐波的频率、幅值和相位。

如果｛d1（n）｝为非平稳周期信号，HHT－FFT法的第一推荐是将包络从信号中一层一层的剥离，也就是把｛d1（n）｝当作上面的｛y（n）｝，再重复上述“提取包络——剥离包络——核 DFT——包络DFT——包核合成”的过程一次，多层包络剥离是一个迭代程序。

4 数字仿真

为了验证HHT－FFT间谐波算法测量谐波与间谐波的有效性，本文进行了仿真研究。为简单起见，首先对包络仅含有单个间谐波信号进行分析，这种情况包络属于周期信号的情况。选取的信号模型是

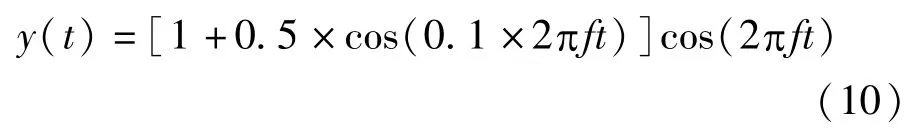
其中f＝50Hz，取采样周波数S＝10，分别对信号进行同步采样和非同步采样（非同步率ζ＝1.01）。

4.1 有同步偏差FFT

由图1可知，非同步采样情况下出现频谱泄漏误差。

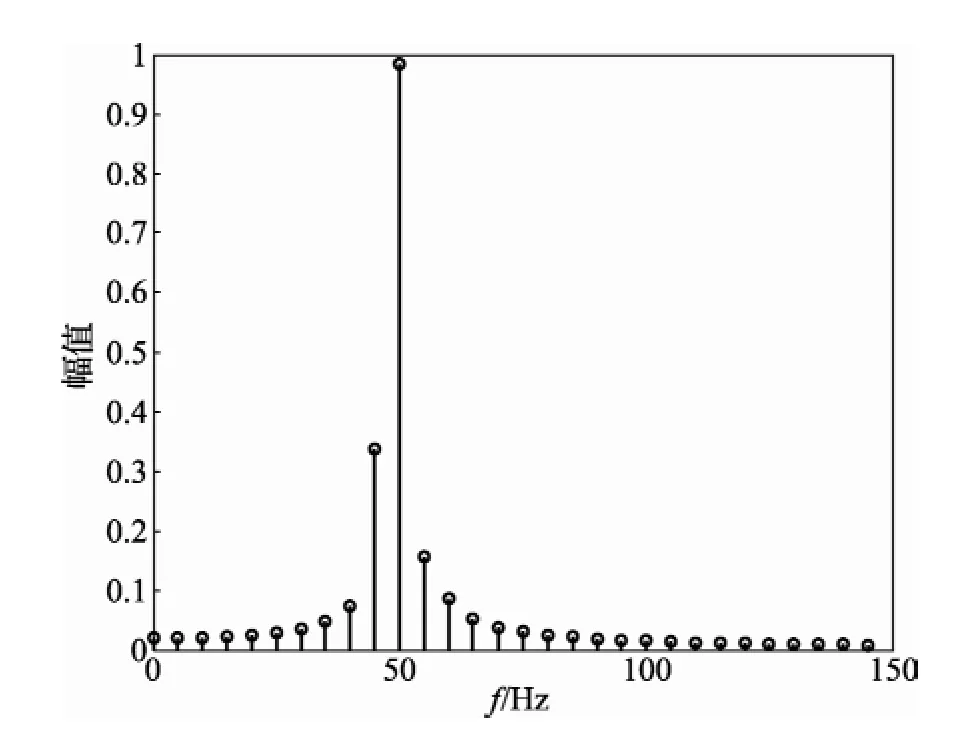
图1 非同步采样FFT的结果

4.2 同样的同步偏差HHT－FFT法

1）采用希尔伯特变换提取包络，见图2。

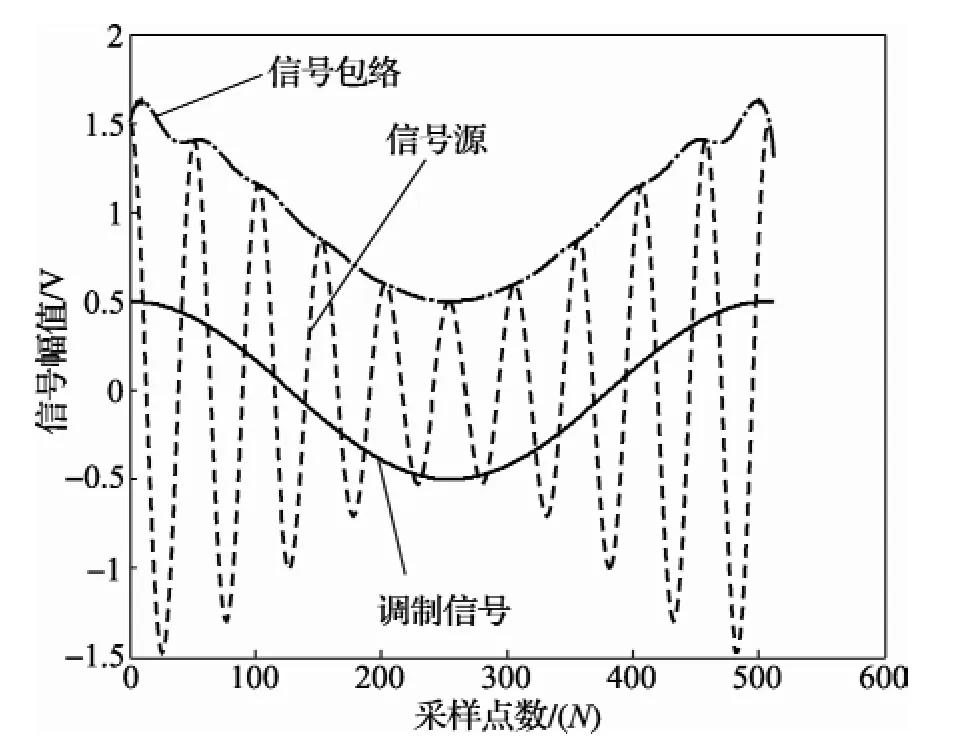
图2 HT提取包络过程图

2）对包络分解求调制信息参数。直接对此包络信号进行HHT运算，可以得到图3结果，即对于包络信息的提取可以得到相应的调幅系数，从图中可以看到包络信号0.1次谐波准确的检测出来。

3）求取信号的谐波与间谐波成份。利用式（4）求取信号的谐波与间谐波参数，具体数据见表1。为了对比HHT－FFT算法与FFT算法的差异，表1也给出了FFT方法求出的谐波与间谐波的数据，从中可以看出，HHT－FFT方法测量谐波与间谐波的精度优于FFT方法。

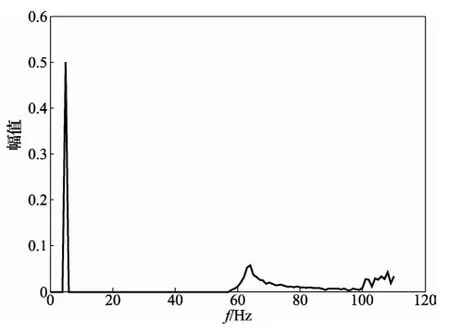
图3 包络信号的各次间谐波幅值

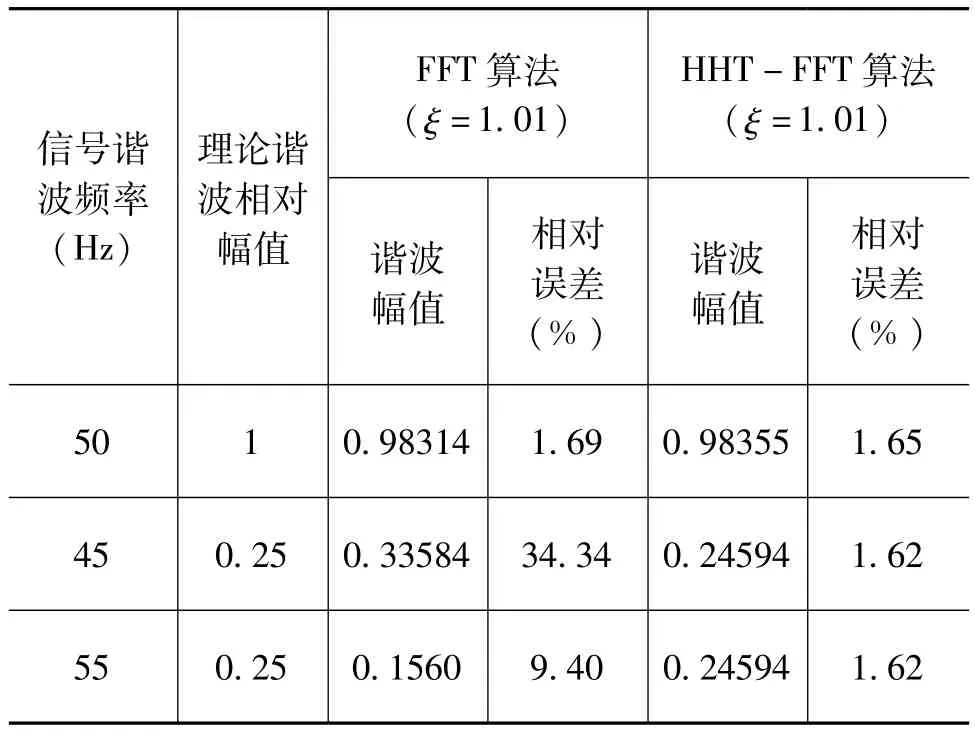
表1 两种算法的数据对比

从表1的仿真数据来看，同样的同步偏差情况下，HHT－FFT算法的分析间谐波的精度要远高于FFT算法。

5 结论

分析幅值波动电力信号的关键在处理包络，首先，间谐波信息主要包含在电力信号的包络之中；其次，包络的出现也会改变整次谐波的幅值和相位。所以，要准确测量谐波和间谐波，最好的方法是提取出包络，并将包络从信号中逐层剥离——这就是HHT－FFT方法。

1）HHT－FFT法是“提取包络——剥离包络——核DFT——包络DFT——包核合成”的一个迭代过程，HHT－FFT法保证了每次进行的DFT都是作用于平稳周期信号；

2）HHT－FFT法在提取包络信号基本排除了整次谐波频谱泄漏产生的虚假间谐波，因而，HHTFFT法能得到更真实、更精确的整次谐波和间谐波。Matlab软件的仿真结果证实了该方法的有效性；

3）在同样的同步偏差情况下本文对标准FFT和HHT－FFT法进行了仿真对比，HHT－FFT方法分析间谐波精度得到提高。

［1］张伏生，耿中行，葛耀中.电力系统谐波分析的高精度FFT算法［J］.中国电机工程学报，1999，19（3）

［2］何益宏，卓放，李红雨，等.Kaiser窗在谐波电流检测中的应用［J］.电网技术，2003，27（1）

［3］Andria G，Savin M，Trotta A.Windows and interpolation algorithms to improve electricalmeasurement accuracy［J］.IEEE Trans Instrum Meas，38（8）：856－863

［4］王柏林，梅永.电力系统谐波分析的近似同步法［J］.仪器仪表学报，2006，27（5）

［5］JIANQiu Zhang and SEPPO J.Ovaska，An adaptivewindow function method for power Measurement［J］.IEEE Trans.Instrum.Meas.，2000，49（6）：1194－1199

［6］FERRERO A.and OTTOBONI R.High accuracy Fourier analysis based on synchronous sampling techniques［J］.IEEE Trans.Instrum.Meas.1992，41（6）：780－785

［7］王柏林.随机环境下电力系统谐波分析算法.电力系统自动化.2008，32（3）

［8］韩松.基于希尔伯特－黄变换的电力系统低频振荡的非线性非平稳分析及其应用［J］.电网技术，2008，32（4）

［8］W.G.Morsi，M.E.El－Hawary，Suitablemotherwavelet for harmonics and interharmonicsusingwavelet packet transform，IEEECanadian Conf.on Electrical and Computer Engineering.2007：748－752.

［10］薛惠，杨仁刚.利用Morlet连续小波变换实现非整数次谐波的检测［J］.电网技术，2002，26（12）

［11］Keaochantarnond T，Boonseng C.Harmonics and interharmonics estimation using Wavelet transform［C］.Transmission and Distribution Conference and Exhibition 2002：Asia Pacific.IEEE／PES 2002：775－779

［12］N.E.Huang，Z.Shen，S.R.Long，et al.The empiricalmode decomposition and the Hilbert spectrum for nonlinear and non－stationary time series analysis［J］.ProcR Soc Lond A，1998，454：903－995

［13］张宇辉，贺健伟，李天云，等.基于数学形态学和HH的谐波和间谐波检测方法［J］.电网技术，2008，32（17）

［17］雍静，孙才新，李建波.间谐波导致的闪变特征及闪变限制曲线［J］.中国电机工程学报，2008，28（31）

10.3969／j.issn.1000－0771.2013.4.01